水槽动力特性数值模拟的新型局部无网格配点法*

曾维鸿，傅卓佳，汤卓超

（河海大学 力学与材料学院，南京 211100）

引 言

水波传播广泛存在于船舶和海洋工程领域.在水波传播过程中，当水波到达近海岸地带时，会引起海岸侵蚀，危及海岸建筑物的安全.在沿海地区，应用水下防波堤保护近海岸建筑物，亟需准确预测水波与这些海上结构物的相互作用[1].

在波浪传播行为研究中，虽然实验研究能够直观地模拟水波的传播，但是由于其受到场地大小、耗时问题的困扰，使得实验研究有着诸多限制.因此，数值模拟在波浪传播力学行为研究中至关重要.经典的数值方法包括有限差分法、有限单元法和边界元法等，这些算法在数值水槽中得到了广泛的应用[2-6].例如： 王本龙等[2]采用有限差分法，初步模拟了波流的相互作用，为进一步研究波流相互作用奠定了基础.王大国等[3]基于有限单元法，对三维完全非线性数值波浪水槽进行了模拟.卫志军等[4]采用拓扑优化技术研究了数值水槽中的晃荡抑制.Koo 等[5]和Christou 等[6]使用边界元法模拟了非线性水波与结构物的相互作用行为.

然而，传统网格类数值方法在求解此类移动边界问题时往往面临重复划分网格导致的计算成本剧增难题.而基于无需网格划分特点的无网格类配点方法在模拟波浪传播问题时，比网格类方法具有固有和先天的优势.近些年来，有众多无网格类方法被应用到数值水槽计算中.例如，黄志涛等[7]采用光滑粒子流体动力学模拟了未满载罐车液体晃荡抑制；Senturk[8]采用径向基函数法，对二维线性和非线性Stokes 波传播进行了数值模拟；李珺璞等[9]采用奇异边界法研究了水下障碍物对水波传播的影响；在此基础上，Zhang 等[10-11]和Huang等[12]采用广义有限差分法（generalized finite difference method，GFDM），对数值水槽进行了模拟研究；Zhang 等[13]采用广义有限差分法结合光滑粒子流体动力学，数值模拟了弱可压缩黏性流的动力特性.

另一方面，一类半解析配点技术——边界节点法[14]被提出，并成功用于声波传播和功能梯度材料热传导分析[15].由于该方法采用了预先满足控制方程的非奇异半解析基函数，因此仅需少量离散节点即可得到高精度的计算结果.然而，类似于其他配点技术，传统边界节点法也会生成稠密矩阵，极大地限制了其在大规模问题中的应用.近年来，Wang 等[16]和Xiong 等[17]先后将局部配点技术与传统边界节点法结合，建立了局部边界节点法（localized boundary knot method，LBKM）.该方法是一种区域化离散方法，仅需要物理域内的离散节点而无需任何网格.对于每个节点，可以首先通过节点之间的Euclid 距离确定具有简单几何的局部子域.然后，每个节点处的未知变量可以表示为该点对应的局部子域内节点处物理量的线性组合.将其代入控制方程和相应的边界条件后可以形成稀疏线性系统，其稀疏系统占用内存小且计算时间短，这使得该方法更适合解决大规模问题.目前该方法已被成功用于声学和对流扩散问题计算.

为了模拟波浪与防波堤的相互作用，防止近海岸建筑物发生侵蚀，本文首次应用局部边界节点法结合二阶Runge-Kutta 法研究了波浪与水下防波堤之间的相互作用.第1 节介绍了数值波浪水槽的控制方程和边界条件以及局部边界节点法的求解方案；第2 节模拟了波浪与水下防波堤的相互作用；第3 节给出了结论.

1 数学模型

1.1 控制方程

本研究采用势流原理进行波浪传播的模拟，即假设液体无黏、无旋、不可压缩，可以得到以下控制方程：

式 中，φ (x,z,t)为 速度势，Ω为水槽计算域.

1.2 边界条件

数值波浪水槽如图1所示，在下边界上，由于假设液体无法自由出入边界，因此满足不可穿透边界条件：

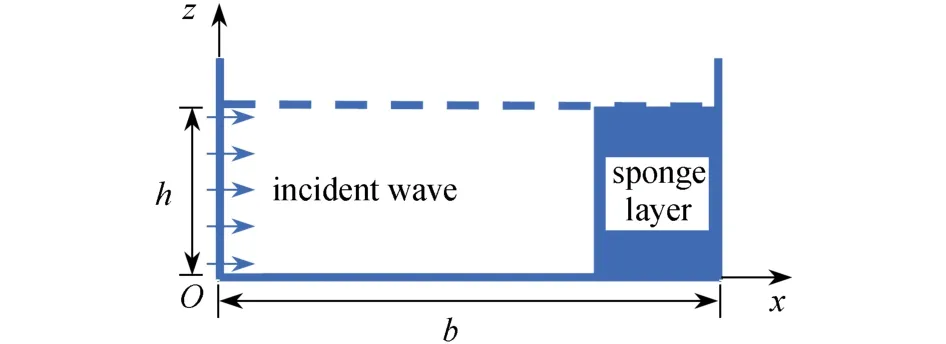
图1 数值波浪水槽的示意图Fig.1 The schematic diagram of the numerical wave flume

式中，n为边界上垂直向外的单位法向量.

数值波浪水槽主要是通过左侧入射边界条件施加入射波，从而达到波浪在水槽内的传播.由于初始水面为静止状态，为了逐步产生入射波从而增强水槽的稳定性，所以引入斜坡函数Rm(t)，故入射边界条件写成

式中，U(z,t)为 入射波速度，Tm为调制时间，根据以往研究经验，本研究中取Tm=2T，T为入射波周期.

为了使到达右端边界的波浪自由射出边界，右端边界采用辐射吸收边界条件[11]：

式中，C为入射波的相速度，对于稳定波而言C=λ/T，λ为入射波波长.

为了防止右侧边界反射波再次进入水槽，从而影响入射波的传播，本文将采用海绵层和辐射吸收边界进行波浪的逐步吸收，在半Lagrange 法的思想上，自由液面需满足动力边界条件和运动边界条件[6]：

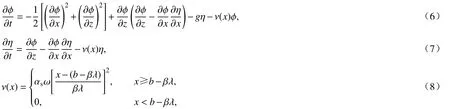
式中，η为自由表面高程函数，ν (x)为 阻尼系数，αs和 β 为调谐因子和长度因子，本文都取成常数1，b为水槽长度，ω为圆频率.

1.3 局部边界节点法

局部边界节点法是一种新型的区域型无网格配点技术，仅需要在计算域内布置离散点而无需任何网格.对于计算域中的离散点，都能够找到包含本身和最邻近的m个 点形 成的局部子域.为了统一，令x(i)=.对于局部子域中m+1个 相邻节点，可以得到以下局部边界节点法公式：

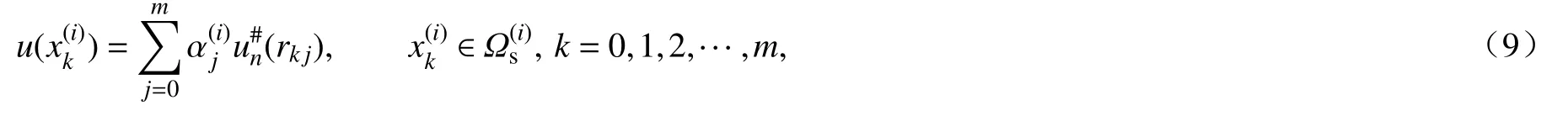
式中，rk j=‖xk−xj‖为 第k个点与第j个点之间的距离，(rk j)为微分算子的非奇异半解析基函数.Laplace 算子的非奇异半解析基函数为平移不变调和函数：

其中，r=[r1,r2]，r1,r2分 别为中心点与其邻近点在x方 向和z方 向上的距离；c为形状参数，其取值与计算域特征长度有关.

式（9）可以改写成如下矩阵形式：

基于移动最小二乘原理的基本思想，需要在每个局部子域中定义以下残差函数：

显然使残差Θ (u)取到最小值的 α(i)为偏微分方程的数值解.则可以对Θ (u)求 α(i)的变分，得到方程组

式中

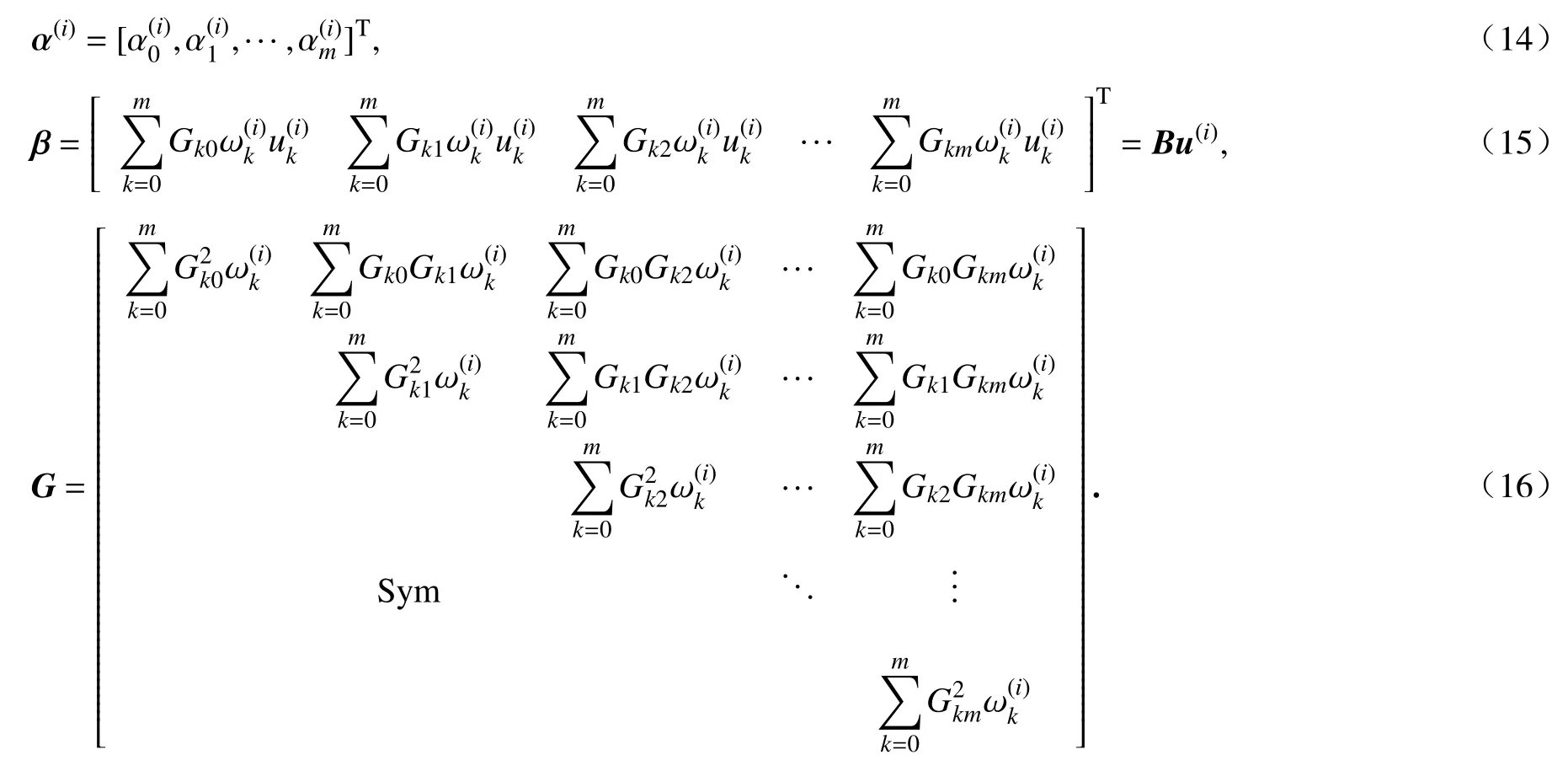
因此，式（13）可以改写为

把式（13）代入式（9）就可以得到x(i)处物理量的近似解：

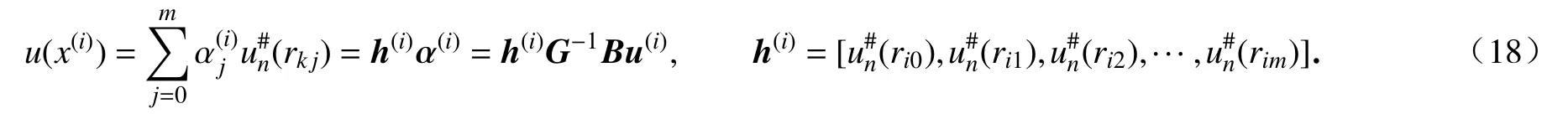
同时，点x(i)处的一阶和二阶导数可以表示为

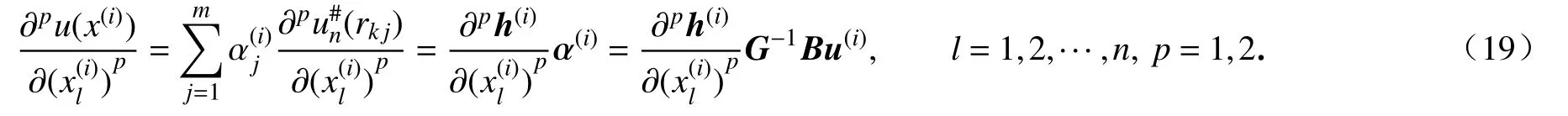
最后把式（18）和式（19）用于离散二阶偏微分方程的控制方程和边界条件，并求解相应的代数方程组，从而近似得到偏微分方程的数值解.

1.4 自由边界离散处理技术

由于式（6）和式（7）是与时间相关的非线性自由边界条件，本文采用二阶Runge-Kutta 法[18]分别离散自由液面边界条件式（6）和式（7）中的时间项，其具体表达式如下：

式中，Δt为时间增量.当离散式（6）时，f与式（6）右端项相同，其中泛函V表示速度势φ；类似地，当离散式（7）时，f与式（7）右端项相同，其中泛函V表示自由表面高程η.

2 数值波浪水槽特性研究

2.1 二阶Stokes 波传播

本节数值波浪水槽如图1所示，长度b和 水深h分别为8 和1.若无其他特殊说明，本小节算例中采用的总节点数、时间间隔、邻近点数固定为N=13 159, Δt=0．005,m=20.对于数值波浪水槽的入射波采用二阶Stokes 波，势函数和自由表面高程函数定义为

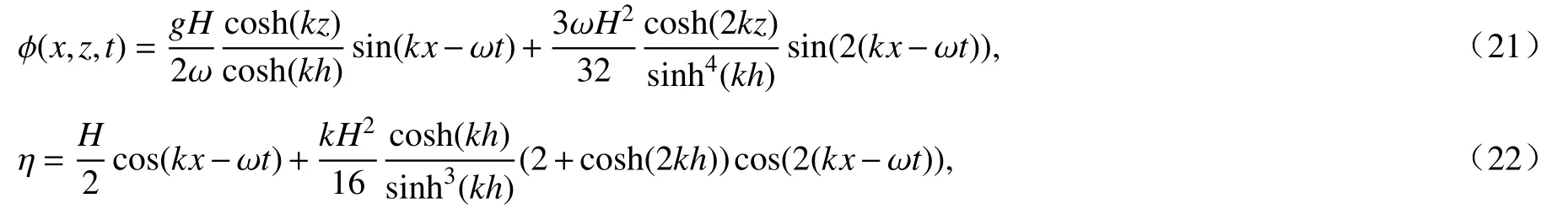
式中，波数k=π，波长λ =2，圆频率ω =5．54，波高H=0．04.

由于满足Laplace 方程的非奇异半解析基函数为平移不变调和函数（式（10）），式中的形状参数对数值准确性至关重要，为了选取合适的形状参数c，使用以下公式确定自由表面高程的均方根误差：

式中，Nnts是自由液面xj∈[λ,2λ]的节点个数，ηA和 ηN分别是自由表面高程解析解（式（22））和数值结果.

此外，为了求解自由液面上速度势 φ及其相应偏导数值∂ φ/∂x和∂2φ/∂x2的均方根误差，使用以下公式确定均方根误差：

式中，δA和 δN分别是自由液面φ，∂ φ/∂x或者∂2φ/∂x2的解析解和数值结果.

首先，形状参数c是影响局部边界节点法求解精度的首要因素，因此确定最佳形状参数是至关重要的.表1给出了在不同形状参数下的均方根误差.从表中可以看出，c∈[0．1,3]的均方根误差都是在误差允许范围之内的，并且c=1时 的均方根误差最小，故本文取c=1作为最佳形状参数.

表1 不同形状参数下二阶Stokes 波的均方根误差Table 1 The RMSEs for 2nd-order Stokes waves with different shape parameters

其次，节点总数和邻近点数是影响计算精度、稀疏系统内存占用和计算时间的主要因素.因此，表2和表3给出了不同总点数和邻近点数下，局部边界节点法与广义有限差分法分别求解数值波浪水槽的均方根误差.从表中可以看出，当总点数和邻近点数较多时，局部边界节点法与广义有限差分法的误差在同一数量级，但局部边界节点法在具有较少总点数或者较少邻近点数时也是可以达到较低误差的.如表3所示，对于局部边界节点法而言，随着邻近点数的增加，误差先减小后增大.并且当邻近点数m=20时，均方根误差最小.所以求解数值波浪水槽时，取邻近点数为20 左右均能保持较高的精度水平.综上可知，相比于广义有限差分法，局部边界节点法可以通过取更少的总点数和邻近点数，使得其稀疏矩阵需要更少的内存和计算时间.

表2 不同总点数下LBKM 与GFDM 的均方根误差Table 2 The RMSE1s of LBKM and GFDM under different total numbers of nodes

表3 不同邻近点数下LBKM 与GFDM 的均方根误差Table 3 The RMSE1s of LBKM and GFDM under different numbers of nearest nodes

此外，表4给出了不同总点数下自由液面上速度势 φ及其相应偏导数值∂ φ/∂x和∂2φ/∂x2的均方根误差.由表4可知，速度势φ 及其相应偏导数值∂ φ/∂x和∂2φ/∂x2的均方根误差均随总点数增加而减小.同时，类似于传统配点技术，局部边界节点法计算得到的数值结果随着偏导数阶数的升高，误差逐渐增大，不过其对应的二阶偏导数值误差均低于4 ×10−2.

表4 不同总点数下φ，∂ φ/∂x 和∂ 2φ/∂x2的均方根误差Table 4 The RMSE2s of φ , ∂ φ/∂x and ∂ 2φ/∂x2 under different total numbers of nodes

从上述讨论可以看出，局部边界节点法能够准确、稳定地求解数值水槽问题.图2展示了不同总点数、不同时间间隔和不同邻近点数下所求得的自由液面在x=4处的高程演化曲线与二阶Stokes 波解析解的比较.从图2(a)～(c)的比较结果中可以看出，除了最初几个周期外，局部边界节点法数值解与二阶Stokes 波解析解基本吻合.由于上游入射边界条件引入了斜坡函数，所以局部边界节点法数值解和解析解在最初存在一定差异是合理的.图2(a)～(c)的比较结果验证了所提局部边界节点法解决方案的准确性、稳定性和一致性.

图2 在x =4处自由液面高程演化图：(a)不同总节点数；(b)不同时间间隔；(c)不同邻近点数Fig.2 Evolution of free-surface elevation at x =4: (a)different total numbers of nodes; (b)different time increments;(c)different numbers of nearest nodes

为了避免波浪在下游边界的反射现象，我们在下游边界设置了海绵层达到吸收反射波的效果，并且海绵层的厚度设置为2.为了验证海绵层的有效性，图3展示了自由液面在4 个不同时刻的轮廓图，从图中可以很明显地看出波浪呈周期性变化，但当波浪到达海绵层以后，波高呈现逐渐减小的趋势，直至为零，所以波浪在下游边界的反射现象基本上不可见，验证了下游海绵层的有效性.

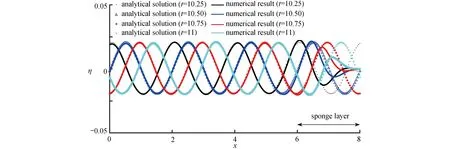
图3 自由表面在4 个不同时刻的轮廓Fig.3 Profiles of free surface along the flume at 4 specific moments

2.2 波浪通过梯形防波堤的模拟

含有梯形防波堤的数值波浪水槽宽度b=30、 水深h=0．4.水下梯形防波堤的尺寸和位置如图4所示.在此算例中，x=0处 的入射条件采用二阶Stokes 波，势函数如式（21）所示，其中波长 λ 、波周期T和波高H分别为3.693，2 和0.02.总节点数N=20 415，时间间隔 Δt=0．005，邻近点数m=20，总时间为12T.在本例中，取Δx=0．025将节点沿x方向均匀分布.对于每个垂直方向，从实心底部到静水表面均匀放置15 个节点，梯形防波堤的节点布置如图5所示.

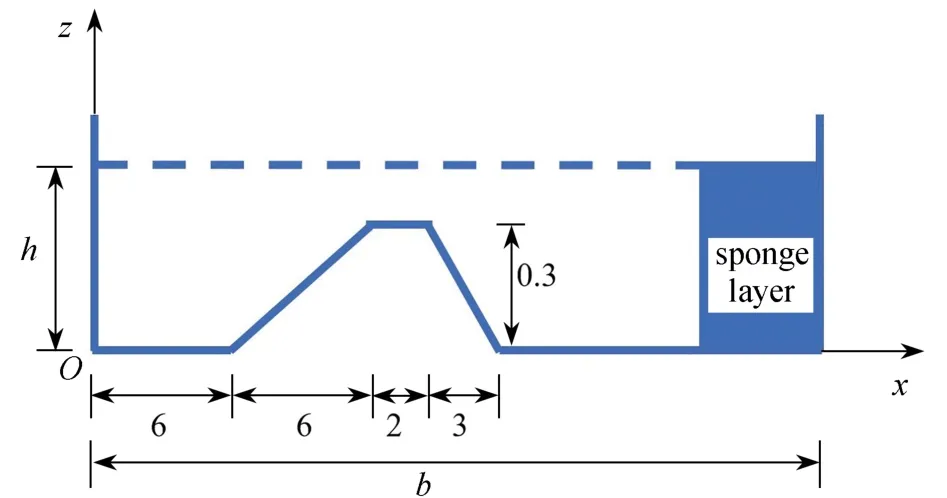
图4 梯形防波堤数值波浪水槽的示意图Fig.4 The schematic diagram of the numerical wave flume with a trapezoidal submerged obstacle

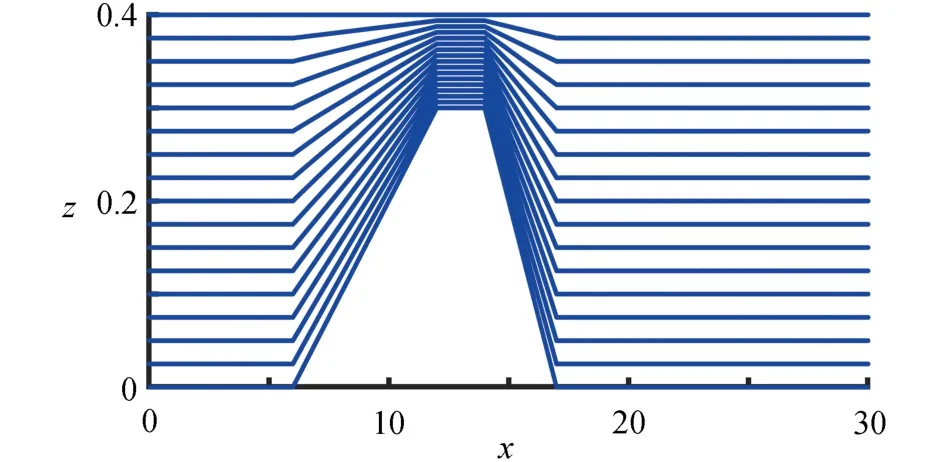
图5 梯形防波堤数值波浪水槽的布点图Fig.5 Distributions of nodes of the numerical wave flume with a trapezoidal submerged obstacle

取自由液面上的5 个点用来记录在最后两个模拟周期(10T～12T)的高程演化曲线，其中5 个记录点的具体位置分别为x=5．7,x=10．5,x=12．5,x=15．7,x=17．3.5 个记录点的高程演化曲线如图6(a)～(e)所示，并与Ohyama 等的实验结果[19]、广义有限差分法结果（邻近点数m=40）进行比较，可以观察到局部边界节点法结果和已有结果具有良好的一致性.从图中可以看出，在x=5．7处，由于波浪还未与梯形防波堤发生相互作用，波峰波谷仍然呈现周期性变化；当波浪与梯形防波堤发生作用后，波峰变得比较陡峭，而波谷变得相对比较平坦，在x=12．5处 表现最为明显，这是因为在较浅的流体区域内，波的非线性进一步增加.此外，自由液面从x=6到x=17在 4 个特定时刻（t=10T,t=10．25T,t=10．5T,t=10．75T）的表面轮廓如图7(a)～(d)所示.由图7可以观察到非线性水波与水下障碍物之间的相互作用.通过比较结果证明，局部边界节点法能够在较小离散区域内准确模拟含有水下障碍物的波浪传播问题.

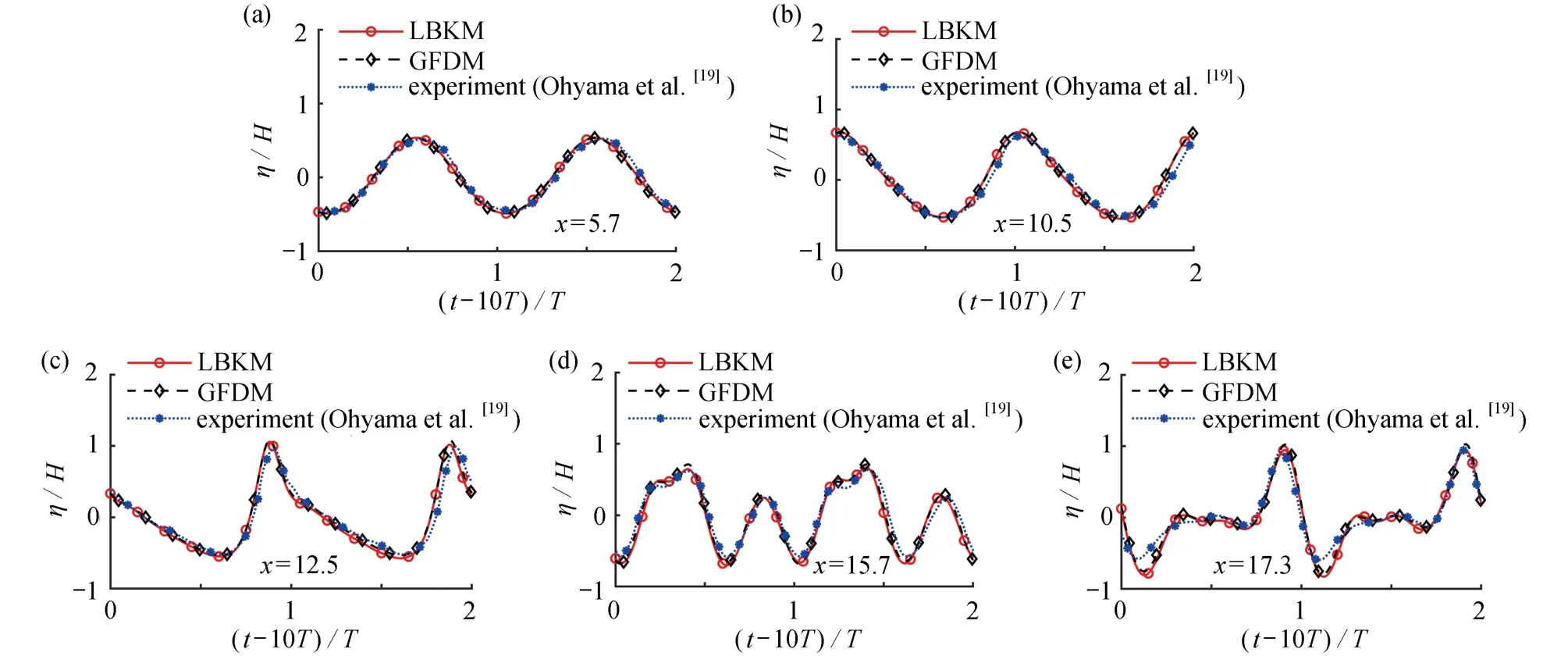
图6 最后两个周期的高程演化Fig.6 Elevation evolution of the last 2 periods

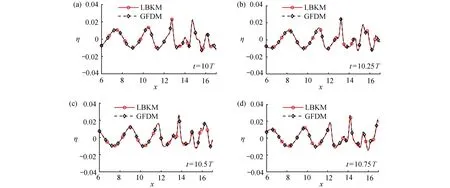
图7 自由液面从 x =6 到 x =17在特定时刻的表面轮廓Fig.7 Free surface profiles from x =6 to x =17 at specific moments

3 主要结论

本文首次采用局部边界节点法结合二阶Runge-Kutta 法求解数值波浪水槽.在数值波浪水槽中，首先通过2.1 小节的算例确定了形状参数的取值范围为c∈[0．1,3]，得到合理形状参数c=1；并且说明局部边界节点法能够在较少的总节点数和较小的局部子域内精确求解数值波浪水槽，更加适合大规模流体力学问题的计算，为大规模流体问题的求解提供了新思路；同时验证了局部边界节点法求解的准确性、稳定性和一致性.其次通过2.2 小节的算例模拟了波浪与近海岸防波堤的相互作用.结果表明，当波浪与梯形防波堤发生作用后，波峰变得比较陡峭，而波谷变得相对比较平坦，这是由于在较浅的流体区域内波的非线性进一步增加的结果.通过比较可以看出，使用局部边界节点法能够在较小离散区域内精确地模拟波浪与近海岸防波堤的相互作用，从而为近海岸防波堤的相关研究和设计提供了数值参考.