雷达杂波建模与评估方法研究

唐文武 袁子乔 赵 博

(西安电子工程研究所 西安 710100)

0 引言

雷达(Radio Detection And Ranging，Radar)是一种利用无线电波进行目标探测和测距的设备，其概念最初形成于20世纪初，并在二战期间得到大力发展。进入21世纪，众多新概念雷达不断涌现，如软件化雷达、认知雷达。当下众多先进技术的加入使现代雷达系统的性能不断提升，包括杂波抑制性能。因此，雷达目标检测性能的评估阶段最直接的做法就是将雷达置于杂波、干扰等背景中。问题在于实际雷达杂波采集势必消耗大量人力物力，并且若要得到不同地理环境完整的杂波数据，势必延长雷达研发周期，不符合软件化雷达提倡的从“使用寿命长”向“研制周期短”转型的研制思想。为此，本文针对两种有效的杂波模拟算法，即零记忆非线性变换法(Zero Memory Nonlinearity，ZMNL)及球不变随机过程法(Spherically Invariant Random Process，SIRP)进行了深度研究。两种算法采用均对杂波幅度与相关特性共同调制，实现不同条件下杂波具有不同幅度统计特性与时间相关特性的仿真。此外，本文提出了一种参数估计仿真验证(Simulation Verification of Parameter Estimation，SVPE)的验证方法。SVPE法利用实际杂波进行参数估计，然后根据得到的参数进行杂波仿真，最后再对仿真数据进行参数验证。该方法的优势在于估计的参数与验证的参数处于不同维度，通过多维度的参数拟合，以实现有效地评估仿真数据的可靠性。

1 雷达杂波特性分析

雷达杂波可定义为目标各种背景的回波，是一种能够影响雷达探测性能的非期望回波信号。在研究雷达杂波时，存在两种不同观点，一种是基于统计特性的假设，另一种是基于混沌特性的假设。统计特性假设认为，雷达杂波幅度统计特性通常服从Rayleigh分布、Log-Normal分布、Weibull分布、K分布等。而Olver等指出海杂波不仅包含可预测的随机分量，还包含不可预测的混沌分量。本文基于Monte-Carlo方法的基本思想进行杂波仿真，简单地说，常规脉冲雷达杂波仿真数据需同时满足一定的统计模型与相关模型。

1.1 雷达杂波统计特性

天线波束照射区域由大量散射单元组成，这些散射单元的回波相互作用形成复杂的雷达杂波。在低分辨率雷达波束照射下，这种散射单元可以认为是空间独立的，因此杂波幅度起伏特性服从高斯分布，在相干雷达中，即服从Rayleigh分布。而随着雷达分辨率的提高，散射单元逐渐表现出相关性与非均匀性，杂波起伏特性逐渐偏离高斯(瑞利)分布。这种非高斯(瑞利)分布杂波可用Log-Normal分布、Weibull分布、K分布等具有更长拖尾的分布进行建模。

1)Rayleigh分布

(1)

其中，为瑞利系数。

2)Log-Normal分布

(2)

其中，为尺度参数，为形状参数。

3)Weibull分布

(3)

其中，为形状参数，为尺度参数。

4)分布

(4)

其中，为形状参数，为尺度参数；(·)为gamma函数，(·)为第一类阶贝塞尔函数。

1.2 雷达杂波相关特性

雷达杂波相关特性是由杂波产生机理决定的，例如海浪整体运动决定功率谱谱峰位置，海浪波纹使得功率谱拓展，因此功率谱能更直观地反映不同频率分量杂波功率。高斯谱和全极谱是两种常用的功率谱模型，下面给出这两种功率谱的表达式。

1)高斯谱

(5)

其中，为平均功率，为杂波多普勒频率，为杂波功率谱标准差，越大，高斯谱谱峰越宽，高频分量功率增大。

2)全极谱

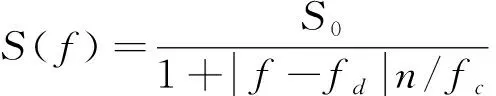
(6)

其中，为归一化功率谱半功率宽度。相比于高斯谱，全极谱具有更长的拖尾，适用于具有更高频分量的杂波建模。

2 雷达杂波建模与仿真

本章针对脉冲雷达，介绍常用的杂波仿真算法及仿真结果评估，常用的仿真算法有ZMNL法及SIRP法。

2.1 地杂波仿真

地杂波多表现在地基雷达回波中，其强度一般呈现出一定的概率分布，可采用杂波的雷达截面积RCS来描述。杂波RCS计算公式为

=

(7)

其中，为散射截面积，为后向散射系数。地表植被、人为活动等众多随机因素导致呈现出一定的概率分布。在低分辨率、高擦地角时，一般可用瑞利分布进行建模，功率谱选用高斯谱模型。本文地杂波仿真采用ZMNL法，仿真参数如表1所列。

表1 地杂波仿真参数

地杂波仿真结果如图1、图2所示。图1显示了地杂波实部(上)与虚部(下)时域波形；采用burg法对地杂波进行功率谱估计，图2左图显示地杂波功率谱理论值与仿真值，采用直方图统计杂波幅度分布概率密度；图2右图显示地杂波幅度分布PDF的仿真值与理论值。从图2可以直观地看出仿真值接近于理论值，后文将采用SVPE方法对仿真误差进行评估。

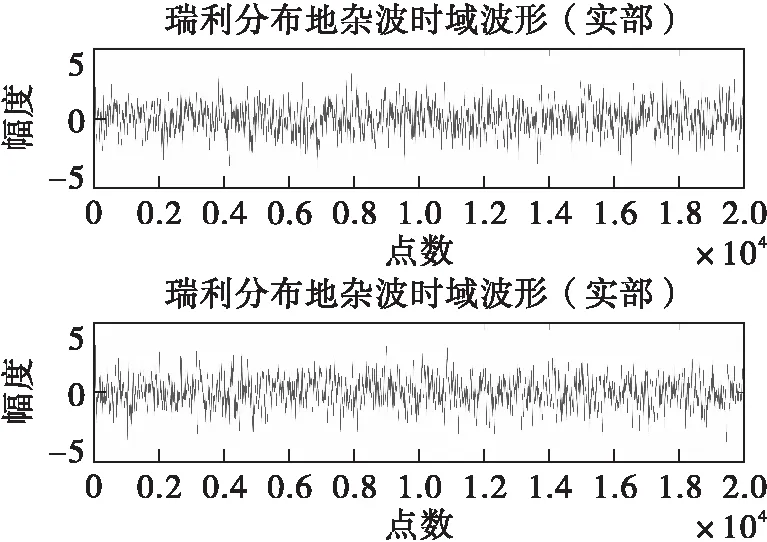
图1 地杂波实部与虚部时域仿真波形

图2 地杂波功率谱、概率密度估计结果

2.2 海杂波仿真

海杂波受风速影响较大，此外洋流、海浪、海面温度等各种复杂因素也决定这海杂波的形态。由于K分布综合考量了海杂波特性及脉冲间杂波相关性，本次采用K分布与全极谱进行海杂波建模。 K分布满足球不变随机过程理论，因此海杂波仿真中本文采用了SIRP算法，详细参数如表2所列。

表2 海杂波仿真参数

海杂波仿真结果如图3所示。采用周期图法进行海杂波功率谱估计，仿真值与理论值如图4(a)所示；采用直方图法估计海杂波概率密度函数，仿真值与理论值如图4(b)所示。

图3 海杂波实部与虚部时域仿真波形

图4 海杂波图

3 基于SVPE的海杂波仿真结果评估

本文针对海杂波进行验证，参考数据来源于网站http://soma.ece.mcmaster.ca/ipix/dartmouth/ datase ts.html上的实际海杂波数据，采用SVPE进行海杂波仿真结果评估的流程如下：

1)对实际低海情杂波进行功率谱与概率密度估计；

2)选择合适的功率谱与概率密度对1)估计结果进行拟合；

3)按2)所选功率谱及概率密度进行相关的参数估计；

4)将上一步所得参数输入模型，进行仿真实验；

5)估计仿真结果的功率谱与PDF，并与(1)结果进行对比；

6)计算实际与仿真杂波的Hurst指数和广义维数，对比评估。

3.1 基于参考数据参数估计的海杂波仿真

在实际海杂波的功率谱估计与PDF统计中，分别采用Burg法与直方图法，结果如图5所示。根据所得结果，经研究发现在采用高斯谱和K分布的组合时，理论值与估计值能达到较好的拟合效果，并且不难得到功率谱标准偏差≈70Hz，中心多普勒频率≈-185Hz。采用二、四阶矩估计K分布尺度参数与形状参数估计，估计结果为：尺度参数≈015，形状参数≈340。根据上述参数进行海杂波仿真，再分别求取功率谱、概率密度函数的实际值、仿真值与理论值，结果如图5所示。

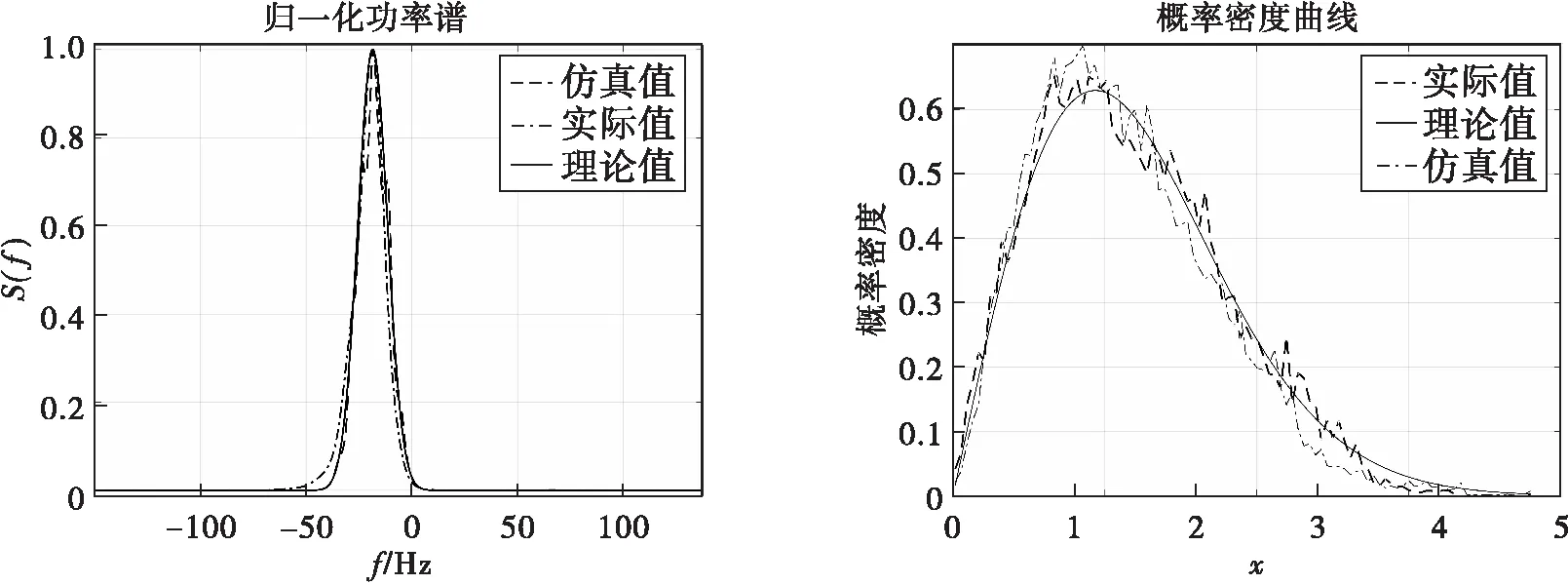
图5 基于参数估计的功率谱与PDF仿真结果

仿真结果显示，功率谱仿真值与实际值总体较为接近，其误差出现在峰值频率附近。另外概率密度曲线误差主要出现在峰值附近，并且由于每次仿真数据是随机的，均方误差也是随机的，而10次仿真均方误差平均值为0.0048，且总体均在置信区间[0 0.01]内。总之，模型误差均在接受范围内。

3.2 海杂波Hurst指数与广义维数

自Mandelbrot提出分形几何的概念，一个集合的维数不再局限于整数，也可能为分数，即分维数。分形被用于描述一些复杂的、不规则的、粗糙的数学模型，分维数则用于测定这种数学模型的维数。分形几何的一种重要特征是自相似性，所谓自相似性，简单地说是用于描述集合内不同尺度子集的结构相似程度，可用Hurst指数标定。

海杂波具有分形几何的特征，因此求取海杂波Hurst指数与广义维数，对海杂波研究具有重要的意义。本文采用R/S重标极差法计算Hurst指数，广义维数分别选取盒维数及信息维数。实验中，实际海杂波数据点数为131072，单次海杂波无重叠采样点数为20000，进行6次仿真并计算Hurst指数与分维数，结果显示仿真值与实际值仅存在微小差别。6次实验Hurst指数仿真值与实际值如表3所示。

表3 Hurst指数实际值与仿真值对比表

盒维数、信息维数仿真值与实际值如表4所示。

表4 盒维数、信息维数仿真值与实际值对比表

4 结束语

本文以软件化雷达为背景，研究了雷达杂波模拟中有效的建模方法与算法，并提出了SVPE验证法。最后结合实际海杂波数据，通过计算Hurst指数及两类分维数对仿真结果进行验证，充分考虑方法可行性与数据可靠性。针对现存问题，如仿真实时性不高、模型存在一定误差等，后续将继续寻找解决方案，同时将研究新的建模方案，如基于混沌理论的杂波建模。