一种改进的和/差波束的米波雷达低仰角目标DOA估计方法

胡 敏 陈伯孝 徐赛琴

(1.航天南湖电子信息技术股份有限公司 湖北荆州 434000；2.西安电子科技大学 西安 710071)

0 引言

米波雷达波长较长，波束宽且阵列孔径受限，因此在低仰角条件下，阵列接收信号不仅包含直达信号，而且包含复杂的多径信号。直达信号和多径信号在雷达接收端产生严重的干涉现象，导致雷达难以对低空目标的仰角进行精准探测与跟踪。低空测角的主要难题包括：一是对于低仰角目标，直达波和多径散射回波通常处于一个波束宽度内，直达波和多径回波的波程差较小，难以从时域、频域和空域对直达波和多径信号进行分辨；二是直达信号与多径信号为空间临近相干源，且受实际阵地地形的影响，复杂多变的多径信号叠加在直达波信号上，直接导致阵列接收信号产生严重的幅相特征畸变现象，现有的解相干类超分辨算法难以获得准确的信号子空间和噪声子空间；三是现有的超分辨算法均基于理想远场平面波模型，而实际的回波信号不仅有直达信号，更包含复杂的反射信号和散射信号，远场平面波模型难以准确描述实际回波信号，信号模型失配问题极大降低了现有超分辨算法性能[6-9]。

目前，超分辨算法主要包括特征子空间类超分辨算法和最大似然算法(Maximum Likelihood，ML)[10]。代表性的特征子空间类超分辨算法有多重信号分类算法[8](Multiple Signal Classification，MUSIC)和旋转空间不变算法[11](Estimation of Signal Parameters via Rotation Invariance Technique，ESPRIT)。MUSIC算法的基本思想是对阵列输出数据的协方差矩阵进行特征分解，得到与信号子空间正交的噪声子空间，利用信号子空间和噪声子空间的正交性实现目标仰角估计。特别地，对于相干源，通过空间平滑的方法，恢复接收数据协方差矩阵的秩，实现目标角度的超分辨估计，即空间平滑MUSIC算法(Spatial Smoothing MUSIC, SSMUSIC)。由于空间平滑方法需要对阵列划分子阵，阵列有效孔径会有一定的损失。ESPRIT算法实现解相干处理的原理是利用子阵间的旋转不变特性，通过估计子阵间的信号子空间，求解旋转不变等式，实现阵列的DOA估计。ML算法利用阵列输出信号的统计分布特征，将接收数据协方差矩阵投影到期望信号空间，实现目标仰角的最大似然估计。当信源数较多时，多维搜索的ML算法具有较大的计算量。通常，采用交替投影最大似然算法(Alternating Projection ML, APML)[13]代替最大似然估计算法，APML算法将多维参数估计问题转化成一维参数估计问题，每次迭代优化过程中仅对众多参数中的一个参数进行优化，极大减小最大似然算法的运算量。然而，这些算法在信号模型匹配、阵地起伏较小时具有良好的估计效果，但当快拍数、信噪比较低或信号模型失配情况下，低空测角性能急剧下降。目前，针对起伏较小的阵地环境下的低空测角问题，文献[5]提出了一种基于地形修正的合成导向矢量最大似然算法(Synthesized Vector ML, SVML)。该算法考虑地形参数信息，建立精确的信号模型，能极大提高最大似然算法的低空测角性能，算法性能较优。

经典的单脉冲测角作为一种实时性高的测角技术，已广泛应用于精确跟踪雷达等，主要适用于单点源的场合。为解决多径环境下的测角问题，Xu[14]等人在经典单脉冲测角技术的基础上，根据直达信号仰角和多径信号仰角关于阵列法线方向的近似对称性，提出了一种对称差波束比幅测角方法。通过特定指向的对称差波束同时接收直达信号和多径信号，将对称相干源的仰角估计问题转化成单点源估计问题，提高了单脉冲测角技术在低仰角条件下的阵地适应性。然而在实际场景下，多径信号和直达信号通常不完全关于阵列法线对称，因此需要进行修正对称差波束。本文从经典多径信号模型出发，在分析单脉冲测角算法原理以及数据的物理特征基础上，提出一种改进的对称和/差波束的低仰角目标DOA估计方法，通过修正的和/差波束中心仰角，提高单脉冲测角技术在低仰角条件下的测角性能及阵地适应性。

1 对称差波束原理

对于经典单脉冲雷达系统，和波束方向图是偶函数，差波束是奇函数，故鉴角曲线是奇函数。在多径信号条件下，误差单脉冲比为一个复数，信号矢量关系图如图1(a)所示，其中Δd和Δi分别为直达波、多径反射波的差波束信号，Σd和Σi分别为直达波、多径的和波束信号。通过对差波束的设计，使得多径差信号Δi仍然与和信号Σi保持同相，则合成的“差通道”信号Δ(=Δd+Δi)与“和通道”信号Σ(=Σd+Σi)仍然保持同向关系，单脉冲比仍然为实数，并且不受反射系数的影响，其矢量图如图1(b)所示。

图1 单脉冲系统和信号、差信号矢量关系图

文献[14]考虑的对称镜面反射情况。对于经典单脉冲系统，当存在镜像对称多径情况下，即θi≈-θd，单脉冲比为

(1)

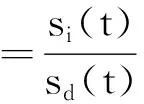
由于直达信号仰角和多径信号仰角关于阵列法线呈近似对称，文献[15]采用对称差波束进行接收，即差波束关于波束中心仰角成偶对称，有UΔ(θ)=UΔ(-θ)，则式(1)的误差信号可表示为

(2)

可以看出，采用对称差波束有效解决多径信号对单脉冲测角算法的影响。而且对称和/差波束的误差信号只与目标仰角有关，而与多径信号的反射系数无关，通过计算误差信号可以准确估计目标仰角。文献[15]给出了波束对称中心在0°的对称差波束的最优权矢量设计。但是在实际阵地，多径反射波和直达波不是完全关于阵列法线的一对镜面对称信号，或者雷达阵列天线通常也是有一定的倾斜，多径反射波和直达波的对称中心也不为0°。

2 基于改进和/差波束的低仰角目标DOA估计方法

2.1 信号模型

经典多径信号模型如图2所示，假设阵列是由M阵元组成的均匀线阵，阵元间隔为d，正常取半波长，快拍数为L。那么阵列接收信号矢量y(t)可表示为

图2 低仰角测高经典信号模型

其中，θd、θi分别为直达波和多径反射波波达角，a(θd)表示直达波导向矢量，a(θi)表示多径信号导向矢量，λ为波长，ρ为反射面复反射系数，s(t)为信号复包络，n(t)表示均值为0、方差为σ2的复高斯白噪声。

2.2 改进的对称差波束权矢量设计

直达信号和多径信号不是镜面对称信号时，是关于某一仰角θt对称的，且差波束在对称中心θt的增益最小。为方便推导，假设阵列同时接收方向为θt+θk的直达信号和θt-θk的多径信号，偏角θk通常不超过波束宽度的二分之一。本文改进的对称差波束的权矢量wΔ,θt需要满足以下两个条件：

1)条件1：对称差波束要求权矢量wΔ,θt在对称中心仰角θt处的增益最小，即

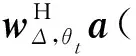
(6)

2)条件2：对称差波束关于仰角θt呈偶对称，指向分别为θt±θk，且权矢量wΔ,θt在波束指向θt±θk处具有相同的增益，即

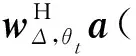
(7)

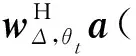
(8)

其中，gk表示差波束在波束指向θt±θk方向上的增益。

令R=[a(θt-θk)a(θt)a(θt+θk)]，d=[gk0gk]T，式(6)、式(7)、式(8)写成矩阵形式为

RHwΔ,θt=d

(9)

根据最小二乘法，差波束的权矢量为

wΔ,θt=R(RHR)-1d

(10)

其中，(RHR)-1可进一步表示为

(11)

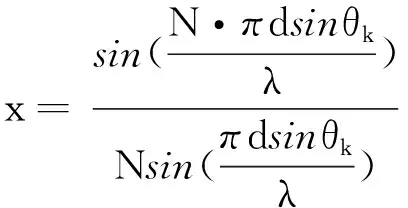
(12)

(13)

因此，归一化的差波束权矢量wΔ,θt为

wΔ,θt=Re[a(θt+θk)]-xa(θt)

(14)

其中，Re[·]表示取实部。采用计算机仿真实验分析所提对称和差波束的方向图及鉴角曲线，仿真参数为24阵元的等距线阵，波长1m，阵元间距为半波长，中心仰角θt=0°。图3和图4分别给出了对称和/差波束方向图及其鉴角曲线。

图3 波束方向图

图4 经典单脉冲与对称波束单脉冲鉴角曲线

可以看出，所提方法的和/差波束均是关于波束中心仰角成偶对称，同时接收直达信号和多径信号，通常误差曲线仅考虑目标仰角大于0的部分。此时，对称和/差波束的鉴角曲线近似是一条抛物线，可采用二次函数近似拟合为

(15)

对式(15)求微分，根据对称和/差波束鉴角曲线得到测角误差为

(16)

可以看出，测角精度与目标仰角和拟合系数k有关，拟合系数k越大，算法估计精度越高。因此要设计最优的对称差波束，使得拟合系数k最大。由文献[15]可知，当θk趋近于0时，对称差波束拟合系数k值最大，此时对称差波束称为“最优”对称差波束。

在理想多径条件下，阵列接收到的直达波与多径反射信号关于中心仰角θt=0°呈对称关系。图5对比中心仰角θt=0°，θk分别取不同的值时，对称和/差波束误差曲线。可以看出，当θk逐渐逼近0°时，误差曲线在中心仰角处的曲率最大，此时测角精度最高。若考虑直达信号和多径反射信号不完全关于θt=0°对称，此时需要进行动态修正。图6给出了对称和/差波束误差曲线由波束中心仰角修正θt=0°到θt=-0.7°的过程。可以看出，修正过程实际上就是对误差曲线进行平移处理。

图5 不同θk对应的对称和/差波束鉴角曲线

图6 误差曲线修正过程

综上，改进的对称和/差波束低仰角目标DOA估计方法的具体步骤可以总结为：

1)按常规数字波束形成(DBF)技术估计目标的仰角，若目标仰角大于一个波束宽度，则应用数字单脉冲测角技术进行仰角测量，否则按一下步骤进行；

2)当DBF的峰值对应的仰角小于一个波束宽度(θ3dB)时，在(0，θ3dB)范围内设置不同的仰角θd，根据雷达架高、地面起伏高度等参数信息，计算反射波的仰角θi≈-arcsin(sin(θd)+2hr/Rd)，再计算直达信号和多径信号的对称中心仰角θt=(θi+θd)/2。其中，Rd为直达波的波程(即目标距离)，hr为雷达阵列天线中心的架高；

3)根据式(14)设计对称差波束，计算关于中心仰角θt对称的差波束的权wΔ,θt；

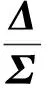
3 仿真数据分析

仿真1：对比动态修正中心仰角算法和固定中心仰角算法测角性能 。

仿真条件：米波雷达阵列结构为24阵元均匀线阵，波长1m，快拍数为1，阵元间距为半波长，波束宽度θ3dB=4.2°，目标仰角范围是0.4°～2°，地面衰减系数为0.8exp(j8π/9)，信噪比30dB。图7给出了SSMUSIC、SVML、文献[14]所提算法和本文算法的测角均方根误差与目标仰角的关系图。从图7可以看出，对于SSMUSIC算法，随着目标仰角的增大，测角均方根误差由0.3°下降至0.11°；对于SVML算法，测角均方根误差由0.27°下降至0.14°；对于文献[14]中的算法，测角均方根误差由0.26°下降至0.11°；对于本文所提算法而言，测角均方根误差由0.22°下降至0.09°，算法性能优于已有的多种超分辨算法，且改进的对称差波束方法性能优于文献[14]提出的算法。

图7 不同仰角测角的均方根误差

仿真2：对比不同信噪比情况下所提方法的有效性。

仿真条件：米波雷达阵列结构为24阵元的均匀线阵，波长1m，阵元间距为半波长，快拍数为1，阵列波束宽度θ3dB=4.2°，单天线信噪比范围是0dB～30dB，目标仰角为0.4°，地面衰减系数为0.8exp(j8π/9)。图8给出了SSMUSIC算法、SVML算法和本文所提算法的测角均方根误差与信噪比的关系曲线。

图8 测角均方根误差与信噪比关系曲线

可以看出，SSMUSIC、SVML及文献[14]的算法性能近似，随着信噪比的增大，测角精度由2.08°逐渐下降至0.27°；对于本文所提算法，其测角均方根误差由1.26°下降至0.18°，在所有信噪比条件下均优于SSMUSIC、SVML和文献[14]提出的算法。因此，所提算法更能适应于平坦阵地环境下的低仰角测高问题，算法性能较优。

4 实测数据分析

对某型米波雷达的两条航线实测数据进行统计分析，阵元结构为24阵元的等距线阵，分别采用DBF算法、APML算法、SSMUSIC算法和本文所提出的对称和/差波束算法对目标点迹数据进行DOA估计。图9和图10分别给出了两条航线的实测数据处理结果。其中，图9(a)和图10(a)分别为两条航线的航迹图；图9(b)和图10(b)分别给出多种算法的测角结果；图9(c)和图10(c)分别给出多种算法的测角误差结果。可以看出，本文所提在低仰角条件下的测角性能优于其他算法，所提算法的测角结果更加平滑、稳定，起伏较小。表1分别统计两条航线的点迹数及各算法的测角均方根误差。对于航线一：DBF算法的测角均方根误差约为0.26°；APML算法的测角均方根误差约为0.44°；SSMUSIC算法的测角均方根误差0.20°；而本文所提算法的测角均方根误差约为0.04°。对于航线二：DBF算法的测角均方根误差约为0.31°；APML算法的测角均方根误差约为0.19°；SSMUSIC算法的测角均方根误差约为0.30°；而本文所提算法的测角均方根误差约为0.04°。实验数据表明，本文提出算法优于SSMUSIC算法和APML算法，测角性能良好，可靠性高，适合部分阵地环境下的低仰角测量问题。

图9 航线一实测数据结果

图10 航线二实测数据结果

表1 实测数据对仰角测量的均方根误差/(°)

5 结束语

本文针对米波雷达低仰角目标DOA估计问题，首先回顾了经典信号模型下的单脉冲测角方法，根据直达波信号与多径反射波信号的近似对称性，设计了最优的对称和/差波束，并在此基础上提出一种改进的对称和/差波束测角方法，通过调整波束中心指向及差波束指向，提高单脉冲测角方法在低仰角条件下的估计精度及其阵地适应性。通过计算机仿真及实测数据验证，所提方法在低仰角条件下算法性能优于已有的多种超分辨算法，可靠性高。