基于改进差分进化算法的机械臂运动学逆解*
2022-04-26沈孝龙王吉芳郭子昇
沈孝龙,王吉芳,郭子昇,马 飞
(北京信息科技大学机电工程学院,北京 100192)
0 引言
近年来,机械臂已广泛应用于工件表面打磨、抛光和去毛刺等作业任务中,尤其是在劳动条件恶劣、存在重大安全隐患的叶片、模具及五金用品打磨行业。此类作业任务需要机械臂与工件进行物理接触才能完成工作且打磨层厚度极小,一般在几十微米内,微小的位置偏差就会导致产品不合格,甚至损坏打磨设备,故需要获得精确的运动学逆解,这是机械臂后续实现力位控制的关键之一。合适的逆解对应机械臂最佳位姿,在使位姿误差最小时,还具有出色的第二性能,如最佳柔顺性、低能耗和避障性等。
通常,求机械臂逆运动学方法主要有两种:封闭解法和数值解法。基于齐次变换矩阵和三角函数的代数法,可解所有逆解,但随关节数增加计算复杂度骤升。根据机械臂构型分析的几何法,解的精度较高、计算量小,但方法通用性差。几何法与代数法均属封闭解法,只有当机械臂几何构型满足Pieper准则[1]时才可使用,通常运用于具有球形手腕结构的机器人运动学逆解中。目前,求解复杂机械臂逆解的主要方法为数值解法,包括雅可比矩阵法、梯度投影法、加权最小范数法等[1]。数值算法耗费计算量,有累计误差,对迭代初值选择敏感并且当矩阵奇异时,运动学逆解无解。综上所述,传统法求机械臂运动学逆解依旧充满困难。
近年来,基于群智能优化的机器人逆运动学分析法为解决逆解问题提供了思路,核心思想是将运动学逆解问题转化为最优化问题。智能优化算法不受机械臂构型限制,求解精度高,方法通用性好且克服许多传统求解方法的不足,受到众多学者的研究。申晓宁等[2]对冗余机械手逆解使用多目标遗传算法,设计两种精英策略,加快收敛速度,仿真表明末端工具可精确到达目标位置。罗天洪等[3]为克服冗余机械臂逆解求解的大计算量和低精度困难,提出基于时变萤火虫群算法的优化方法,显著提升逆解精度与稳定性。杨惠珍等[4]针对逆解存在的多解与通用性差问题,设计一种自适应小生境遗传算法,仿真表明算法精度高,收敛快,可求唯一解。冯晨旭等[5]使用改进天牛须搜索求4DOF机械臂逆解,可在短时间内,以较高精度求得全部解。石建平等[6]基于改进克隆选择算法,克服了常规方法无法有效求解冗余机械臂逆解的问题。林阳等[7]运用多种群遗传算法处理不适用Pieper准则的冗余机械臂逆解问题,有效避免了算法的局部收敛和稳定性差的缺点,使收敛精度和速度显著改善。何兵等[8]设计的复合形差分进化算法,以较少计算开销即可求出高精度位置逆解且能求得全部解。谢习华等[9]对9自由度机械手使用改进差分进化算法求解出位姿误差最小时的运动学逆解。
但现有群智能优化算法,基本上只是限制位置误差最小,姿态误差精度低且极少考虑满足最小位姿解下的各关节柔顺性与能量消耗。受上述有关智能优化算法的启发,在此基础上提出一种改进差分进化算法的机械臂运动学逆解方法以提高位姿收敛精度,将算法用于6R机械臂逆解,与不同改进算法进行仿真实验对比,结果表明所提算法平均在173代就能获得高精度位置逆解, 10-7m相对文献[9]250代快。同时,使机械臂具有最佳柔顺性与较低能量消耗。为验证算法通用性又对冗余机械臂进行逆解实验,寻优成功率100%,相对文献[16]32%提升显著。
1 机械臂的数学模型及代数法逆解
1.1 正运动学模型
仿真实验主要以库卡KR210 L150-2机械臂的运动学逆解为研究对象,进行算法的改进研究与验证。机械臂模型及连杆坐标系如图1所示。
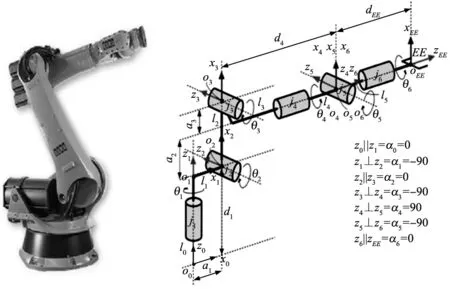
图1 机械臂模型及连杆坐标系
由D-H法,连杆坐标系i-1到i的变换由关节角θi、连杆扭角αi、连杆偏距di、连杆长ai4个参数描述,由图1及产品数据手册可得表1。
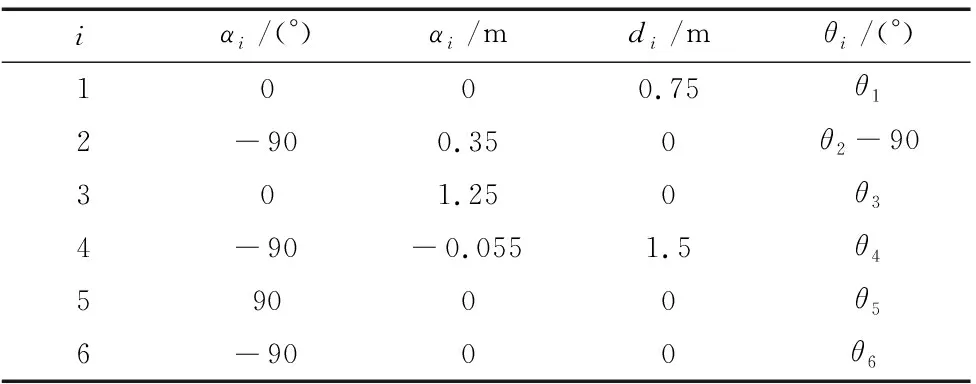
表1 库卡KR 210 L150-2改进D-H参数表
相邻两连杆的位姿变换过程可用i-1Ti表示,通常由式(1)的齐次变换矩阵表示。
(1)
式中,cαi-1=cos(αi-1);sαi-1=sin(αi-1);cθi=cos(θi);sθi=sin(θi);i=1,2,...n。
机械臂末端相对基坐标系的位姿矩阵0T6,如式(2)所示。
(2)
式中,R=[n,o,a]为末端工具的姿态信息;P=(px,py,pz)为末端工具的位置信息。把表1各参数带入式(1)和式(2)即可得到各位姿参数方程。
1.2 基于代数法求得的逆解
库卡KR210 L150-2机械臂符合Pieper准则,根据机械臂的正运动学方程,使用矩阵逆乘的代数法可以得到8组解。具体计算过程不在本文论述,下面给出在给定位姿为式(3)时计算得到的八组逆解,如表2所示。
(3)
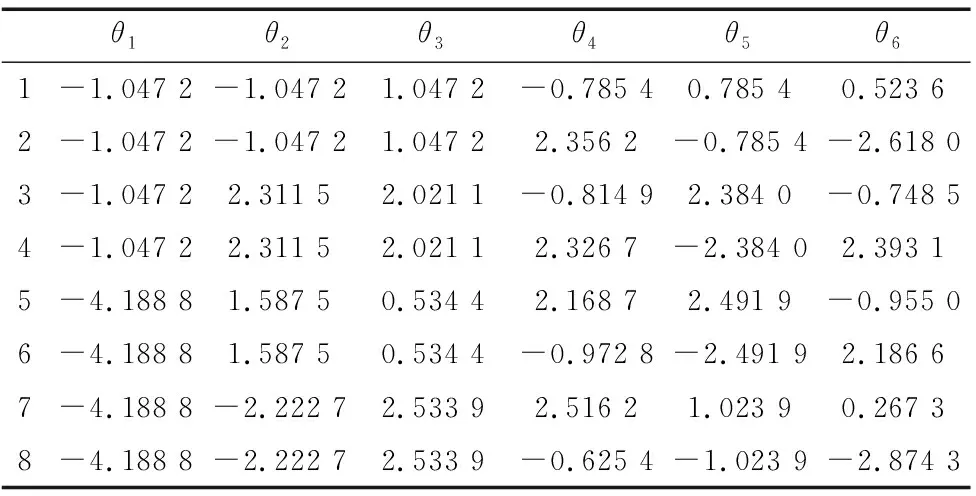
表2 代数法求得给定位姿的八组逆解
2 适应度函数
由1.2节知,当给定库卡机械臂一组位姿时,可得8组逆解。若为冗余机械臂,会存在无穷多组逆解,通常需要设定一些约束来求得最优解。实际生产中,在满足机械臂末端位置误差时,通常还希望机械臂运动具有低能耗、柔顺性等。
2.1 位姿误差目标函数
设机械臂末端目标位姿矩阵为:
(4)
定义位姿误差目标函数为:
F=ε*|P*-P|+|R*-R|
(5)
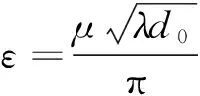
2.2 最佳柔顺描述
“最佳柔顺性”即各关节角从初始位姿运动到目标位姿时,所有关节转角之和相对最小。我们知道机械臂的大臂比小臂质量大,为使运动耗费能量少且平稳,应多运动小臂,从而提升臂的工作效率。最佳柔顺与能量约束[11]描述如下:
(6)
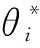
2.3 适应度函数
将最佳柔顺及能量约束与位姿目标函数相结合,构建适应度函数:
F(R,P,θ)=γF(R,P)+(1-γ)f(θ)
(7)
γ=1/2×e-F(R,P)+1/2
(8)
式中,γ为位姿误差动态调节系数,用于控制进化方向。差分进化开始时,F(R,P)较大,γ≈0.5,随着进化开始,F(R,P)逐渐变小,γ→1。适应度函数这样构建,有利于维护F(R,P)与f(θ)在进化过程中的平衡,使进化方向更加合理。
3 改进的差分进化算法
差分进化(differential evolution,DE)是基于实数编码的进化算法,由变异、交叉和选择3个基本操作组成[12],与经典遗传算法一脉相承。但因其有出色的全局优化性和鲁棒性,广泛在连杆机构的杆长优化、机械臂轨迹优化、混合流水车间调度等工程优化领域运用,但在机械臂逆运动学求解应用少有人研究。算法通过模拟达尔文“优胜劣汰、适者生存”思想,利用上代向量间差分的原理进行种群的进化更新产生变异新个体以求得所优化问题的最优解[13]。算法优劣主要由初始种群产生策略和变异、交叉策略决定。
3.1 改进的种群初始化
经典DE算法采用随机分布法产生初始种群,难以保证个体多样性,使最优解质量与收敛速度并不理想[14]。混沌运动独特的随机性和遍历不重复性对生成多样性的个体有优势,可以促使初始个体尽可能均匀分布于搜索空间。为提升最优解质量和保持群落里个体多样性,采用混沌映射对初始种群及子代种群进行改造,以提升算法优化能力。一维Logistic映射为:
xμ+1=δxμ(1-xμ),x∈[0,1]
(9)
式中,xμ为混沌变量,在δ取值为4时,系统表现为混沌态,于[0,1]范围随机取值。(0,0.25,0.5,0.75,1)称作一维Logistic映射的5个不动点。对群落初始化的改造其实就是将混沌映射与随机分布法产生的两个群落内的个体适应值逐一比较,挑出NP个最优个体当作初始群落,方法如下:
步骤1:随机分布法生成群落A。
xmn,1=xnmin+rand×(xnmax-xnmin)
(10)
式中,m=1,2,...,NP;n=1,2,...,D;rand∈[0,1];xnmax、xnmin为第n个变量的上届与下届。
步骤2:随机产生数x1∈(0,1),但x1不可以为上述5个不动点,从x1起,根据式(9)产生混沌序列。
{x1,x2,...,xNP×D}
(11)
步骤3:将式(11)按行排布生成一混沌矩阵。
(12)
步骤4:把式(12)的元素映射到种群个体每一维,xmn∈[xnmin,xnmax],得到混沌初始群落B。
xmn=xnmin+xm,n×(xnmax-xnmin)
(13)
步骤5:计算群落A∪B中所有元素适应值,按从小到大顺序排,选择前NP个元素作为最终的初始群落P。
3.2 基于二次混沌映射的子代重构
随着迭代的不断进行,种群中随机分布的个体会逐渐聚集,此时可能发生局部收敛情况,从而难搜索到全局最优解。为此,本文每隔一定代数M重构种群,在迭代过程中,剔除部分高聚集个体,通过迁移因子产生一些新个体补偿,来保持种群多样性,使搜索能跳出局部最优解,提高全局收敛能力。
假设当前最优个体的适应值为best_unit_value,M代前最优个体的适应值为lastbest_unit_value,用二者之比表示进化效果,即:
(14)
σ越小,进化效果越好,反之越差。σ>Φ时,通过二次混沌映射对子代群落进行重建,Φ为设定的阈值,方法如下:
步骤1:执行3.1节的步骤2与步骤3。
步骤2:把式(12)的元素映射到群落个体每一维,xmn∈[xnmin,xnmax],产生混沌迁移量。
(15)
步骤3:基于子代群落P,按下式进行混沌迁移,生成一新群落C,g∈[0,1]为迁移度。
(16)
步骤4:计算群落P∪C中所有元素适应值,从小到大排,挑出前NP个元素到下一次迭代的父代群落PG+1。
3.3 基于对称映射法的越界处理
经变异操作后的试验个体可能会越出边界范围,需要对这些个体处理,使用最多的方法是随机再初始化法,但随机性强,易丢失原变异个体信息。本文选用对称映射法将越界个体变量转换成一个相对于边界对称的数值,可减小随机性,保留原部分变异个体信息,提高算法收敛精度。方法如下:
(17)

3.4 进化模式选择
变异操作时,需从种群中随机选取3个不同个体xp1、xp2、xp3,且i≠p1≠p2≠p3,DE/rand/1为:
hij(t+1)=xp1j(t)+F(xp2j(t)-xp3j(t))
(18)
DE/best/1为:
hij(t+1)=xbj(t)+F(xp2j(t)-xp3j(t))
(19)
式中,F∈[0,2]为缩放系数;p1、p2、p3为个体在种群中的序号;xbj(t)为当前进化种群中最优个体。
DE/rand/1进化模式虽有全局搜索的优势,但收敛速度慢。DE/best/1进化模式以当前进化种群中最好适应值的个体作为基矢量,具有出色的局部搜索能力和快速收敛特性,但容易搜索停滞和存在过早收敛。为此,本文设置一选择条件,fitness>L时采用式(18)进化形式,其它情况采用式(19)进化形式,可充分结合两者的优势,克服各自不足。L为希望达到的位姿精度,fitness为当代种群最优适应值。
3.5 自适应变异因子F
变异因子F对种群多样性与收敛性影响较大,我们希望进化前期,F值较大,有助于全局搜索,保持种群多样化。在后期收敛时,F值希望较小,有助于在收敛区域进行局部搜索,提高收敛速率和搜索精度。为此,设计F在[0.8,0.4]范围内动态变化。
(20)
式中,N为当前迭代数;G为最大迭代数;F0为最小变异因子;Fi为自适应变异因子。
4 仿真与实验验证
4.1 参数设置
本文将第3节改进的差分进化算法(CBDE)用于库卡6R机械臂进行逆运动学求解,并将其求解结果与经典DE、CDE算法(只采用文中第3.1与3.2节改进方法)及BDE算法(进化模式为best/1)的求解结果进行对比分析。为验证所提算法的通用性,又选取一7DOF冗余机械臂验证。与算法相关的参数如表3所示。
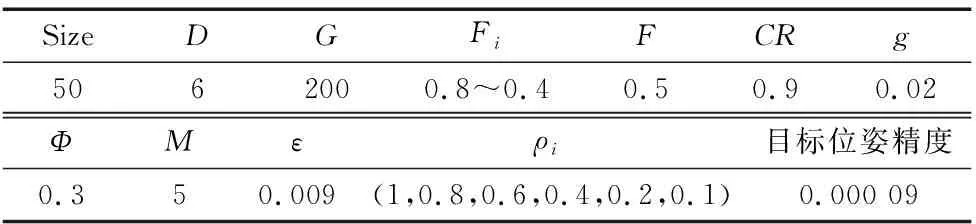
表3 算法相关参数设置
在仿真试验中,所有算法采用MATLAB R2016 b进行编程,计算机配置为:Intel Core i5-4210、2.90 GHz、12 GB内存、Windows10操作系统。
4.2 算法优化性能对比分析
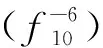

表4 不同算法的性能指标统计

表5 不同优化算法最优逆解及代数法8组逆解对应的机械臂位置
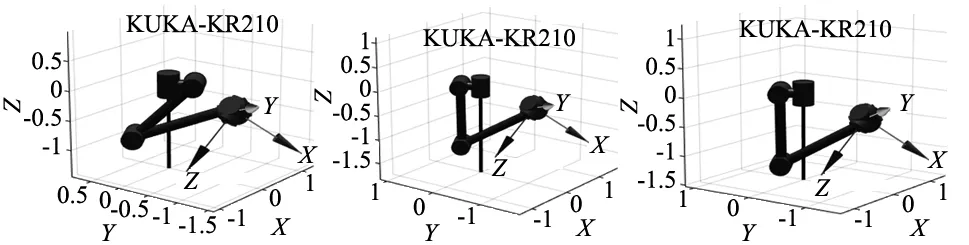
(d) 第四组逆解位姿 (e) 第五组逆解位姿(f) 第六组逆解位姿
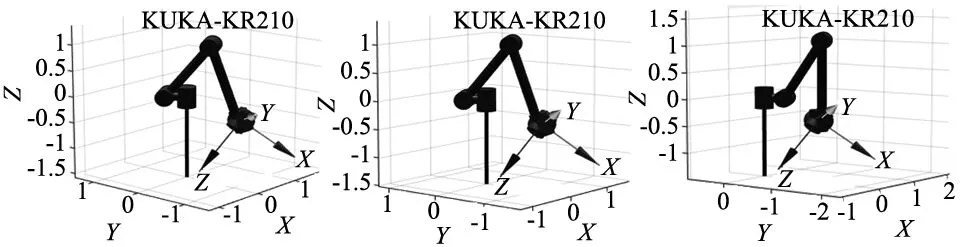
(g) 第七组逆解位姿(h) 第八组逆解位姿(i) DE算法最优逆解位姿
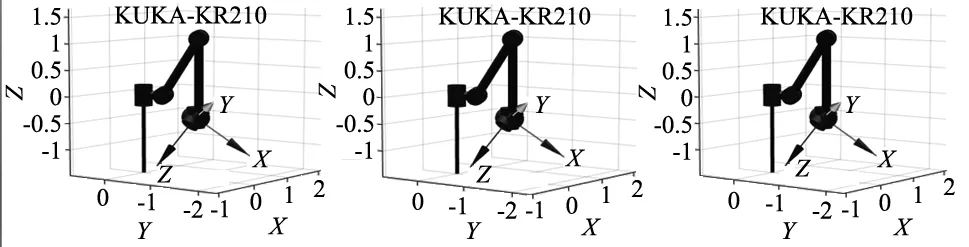
(j) BDE算法最优逆解位姿 (k) CDE算法最优逆解位姿 (l) CBDE算法最优逆解位姿
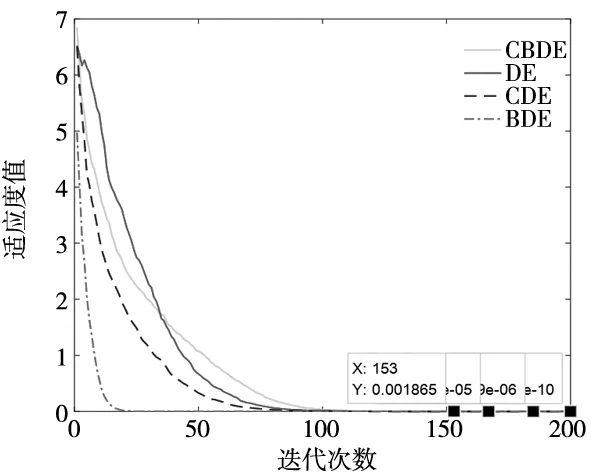
图3 各算法适应值变化曲线
由以上实验数据可知,相比传统代数法求得的逆解如表5所示,群智能优化算法精度更高,且最优逆解均为产生目标位姿的角度,从位姿模型图可以看到最优解满足最佳柔顺性与较低能量消耗。表4在G=200时,经典DE算法位姿与位置成功率最低,位姿误差在万分之一范围内成功率只有94%。Best/1进化模式,虽然最低适应值可以到10-15数量级,但位姿误差在万分之一范围内的成功率仅为92%,并且有时会陷入局部最优,误差很大。改进的种群初始化与种群二次重构CDE算法,位置成功率仅72%。而CBDE算法位姿与位置成功率及位姿误差在万分之一内均达到100%,成功集合了各家优点。从图3各算法平均适应值变化曲线看,Best/1进化模式收敛最快,但存在局部收敛,平均适应值0.001 865 181。CBDE算法与CDE及经典DE算法相比虽然前期收敛速度较慢,但达到10-6适应值平均代数最低且最终平均适应值也最低,而且能够满足各项成功率100%。综上所述,CBDE算法能有效求取机械臂运动学逆解,且求解精度高,所需迭代次数少,最优逆解满足最佳柔顺性与较低能量消耗。
4.3 冗余机械臂逆解实验
为验证CBDE算法求冗余机械臂逆运动学的有效性,选7DOF YuMi 14000 ABB机器人左臂进行运动学逆解实验,其具体的D-H参数见文献[15]。目标函数为式(5) ,适应度函数为式(7)。用MATLAB Robotic Toolbox求[-pi/4pi/4pi/6 -pipi/4 -pi/6pi/3]关节角下的位姿作为给定目标位姿:
(21)
与文献[16]对比,参数设置为Size=100、G=700、D=7。因YuMi机器人各连杆质量轻,这里式(7)中ωi均为1,只要求各关节转角差,和最小,其余参数设置与前述相同。将算法独立连续进行100次逆解运算,仿真试验的第700代平均适应值(F700)、位姿成功率(S1)及寻优成功率K如表6所示。其中,
(22)

表6 冗余机械臂逆解实验结果
实验时,平均在第340代适应值到10-5数量级,位置精度小于0.000 1 mm,姿态精度小于0.000 1 rad,成功率100%。表6中加*为文献[16]结果,可以看出所提算法均优于它。用机器人工具箱绘制在给定角度,最小适应值及最差适应值下的位姿图,可以发现图形及各参数数值基本一致,有一点点差异是因为代入绘制模型图的角度小数位数不全所致。综上所述,CBDE算法可以求解冗余机械臂逆运动学。
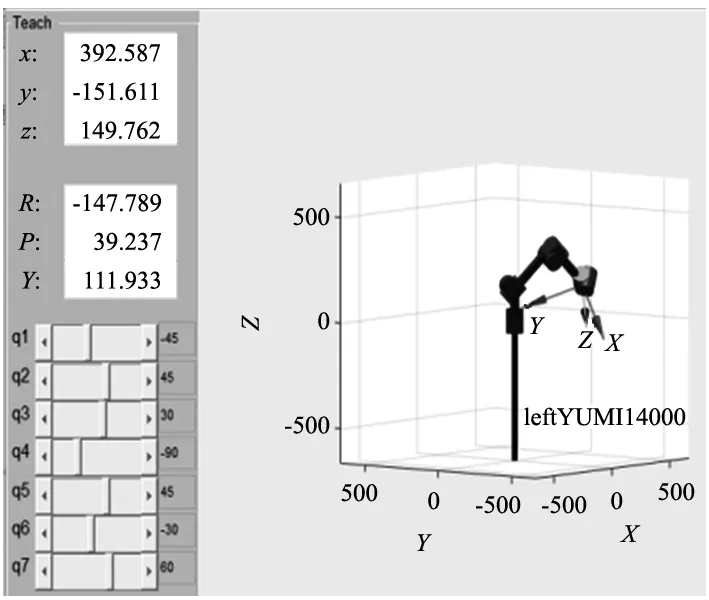
(a) 给定角下位姿图
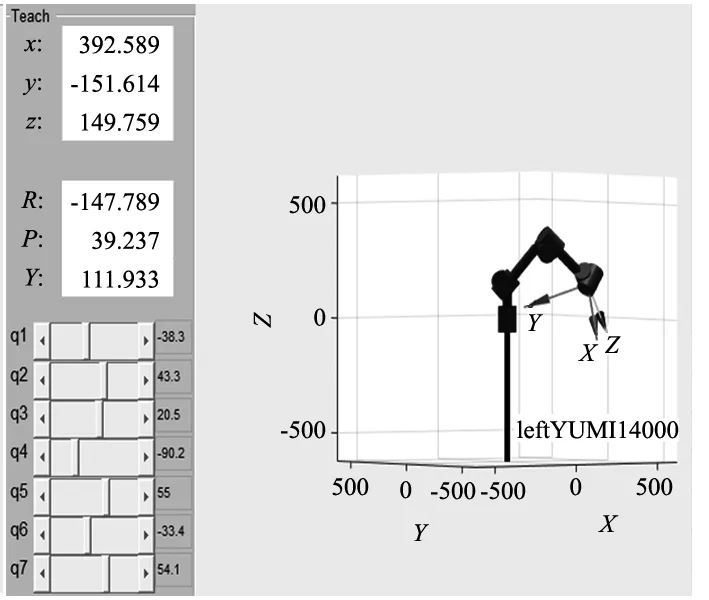
(b) 最优适应值下位姿图
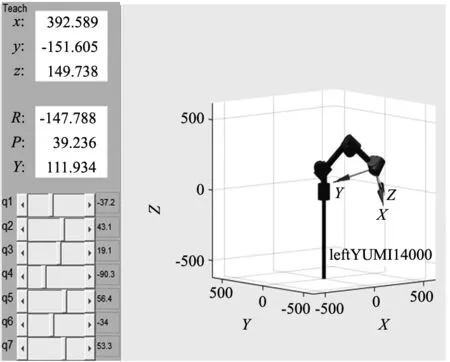
(c) 最差适应值下位姿图
5 结论
所提出的基于改进差分进化算法的机械臂逆运动学求解方法,能够有效提升算法的收敛精度与速度,使逆解精度提升,降低求解复杂度,方法通用性强,对两种机械臂逆解实验成功率均为100%。
(1)对6R机械臂的逆解实验,平均200代时适应度值达10-10数量级,与文献[9]相比,目标函数简洁高效、易于编程实现。在较低迭代次数下,不仅使末端位姿误差满足要求,还使机械臂各关节具有最佳柔顺与低能耗的第二特性。
(2)对7DOF YuMi左臂逆解实验,MATLAB仿真结果表明,在给定位姿精度下,算法对冗余机械臂的逆解成功率亦为100%且与文献[16]对比发现,所提算法各评价指标均最优,证明算法具有较强通用性。
