矢量解耦下的五轴数控系统路径平滑算法*
2022-04-26石继超赵现朝霍晓锐黄孟杰
石继超,赵现朝,霍晓锐,黄孟杰
(上海交通大学机械与动力工程学院,上海 200240)
0 引言
航空航天领域中很多关键零部件具有复杂的外型曲面结构,为确保零件的正常工作需要保证足够的加工精度,这对于数控加工提出了很大的挑战。而五轴混联机床具有高的加工自由度,更好的加工柔性,因此可用于形状复杂等零部件的加工。
对复杂的零部件来说,为了准确加工出零件的形状,要求五轴机床以特定的姿态在允许的误差范围内到达特定的位置。由于五轴机床的非线性,在折线段之间运动时各个驱动轴速度、加速度以及加加速度会出现突变。因此需要对零件形状控制点形成的线性运动路径进行平滑处理[1]。路径平滑处理主要分为两个阶段,分别为局部平滑和全局平滑,其中局部平滑主要针对于折线段中尖锐夹角,全局平滑则主要针对于刀具最终整体运动路径的平滑性[2]。
局部平滑算法旨在通过平滑出的曲线在误差范围内拟合出高阶平滑的轨迹曲线。SUN等[3]通过结合B样条插值算法和最小二乘(LS)逼近算法,提出了一种新的使用LS-B样条逼近轨迹的曲线平滑算法,并且提出了一种多相结构来实现该算法,该算法在已知轨迹数据以及误差时,能够同时保证较高的重构精度以及连续性。AMMAD等[4]提出了一种用于插值数据点的算法,构造出B样条基函数及其导数的矩阵,并使用LU分解方法对未知点进行求解。YEH等[5]提出了一种通过任意阶数B样条逼近曲线的方法,且自动确定实现高逼近的节点矢量,从而在保证拟合的准确性的前提下也保证了算法的实时性。
全局平滑算法旨在生成最终加工的平滑路径曲线。XU等[6]提出了一个框架用于计算B样条曲线,并且可以在拟合精度内逼近微线刀具路径,首先提出了双弦误差测试确定出支配微线刀具路径整体形状的支点分布,并扩展了一个几何偏差模型用于估计控制多边形与B样条的整体误差,集成到全局刀具路径优化中,大大减小控制点数量。LIU[7]通过对连续线段进行NURBS曲线拟合获得可靠的NURBS曲线格式的刀具路径,在刀具位置数据的分割阶段中,通过拐角角度测试以及双弦误差测试提出刀具路径数据点的参数化以及节点划分策略,有效控制拟合误差。
本文提出了一种新的路径平滑算法,采用矢量解耦的方式分别对机床加工运动轨迹以及运动姿态进行平滑。在运动轨迹方面,结合约束条件模型,通过Q-Learning算法生成一条满足G2连续性的轨迹。在运动姿态方面,附加曲率与姿态方向角变化率的约束,通过降维计算使用离散积分得到姿态方向角。
1 局部轨迹平滑
局部轨迹平滑是指对形成尖锐夹角的控制点位置坐标之间构成的微短线性路径进行平滑处理,生成一条具有G2连续的刀具平滑路径。对于曲线满足连续光滑路径的主要有p阶Bézier曲线、p阶B样条曲线以及p阶NURBS曲线,均可在各自的节点区间中满足p-1次连续,因此为满足G2连续条件,故可确定阶次为3。此外,对于Bézier曲线来说,阶次会随着控制点个数的变化而变化,以及任意一个控制点的改变都会影响到全局的曲线形状,局部性较差;而对于B样条曲线来说,相对于NURBS曲线自由度较差,因此最终选择3阶NURBS曲线作为轨迹生成曲线,并以此为基础,建立数学模型,确定目标函数,使用强化学习Q-learning的算法获取最终解。
1.1 NURBS曲线
NURBS曲线在B样条曲线的基础上为每个控制点引入一个权重的参数,增加曲线形状调整的自由度,该曲线表达式[8]如式(1)所示。
(1)
式中,u为NURBS曲线中的节点参数;p为曲线的阶数;Pi为控制点的坐标;wi为控制点的权重;Ni,p(u)为NURBS曲线的基函数表达式。
NURBS曲线由于其表达式的特殊性,主要具有以下性质:
(1)在每个节点区间[ui,ui+1),曲线保证p阶连续性;
(2)在每个重复度为k的节点,曲线保证p-k阶连续;
(3)节点参数u个数为m+1,控制点个数为n+1,曲线阶数为p,满足式(2);
m=n+p+1
(2)
(4)当u0=…=up时且um-p=…=um时,NURBS曲线与控制边界的起始边和终止边在端点处相切。
由性质(1)和性质(2)可知,在保证曲线具有G2连续性的前提下,为尽可能减小计算量最终选择p为3,并且在中间节点处重复度k只能为1。
由性质(3)可知,在局部路径平滑中控制点个数固定,且曲线阶数p为3,因此节点参数个数m可计算得出,因此NURBS曲线的可调整自由度分别为u的分布均匀性以及权重wi的变化。
针对于节点分布带来的影响,分别采用均分分布以及不均匀分布的方式对同一控制边界进行NURBS曲线绘制,如图1所示,可知u节点均匀分布时NURBS曲线以控制边界角平分线为轴对称分布。
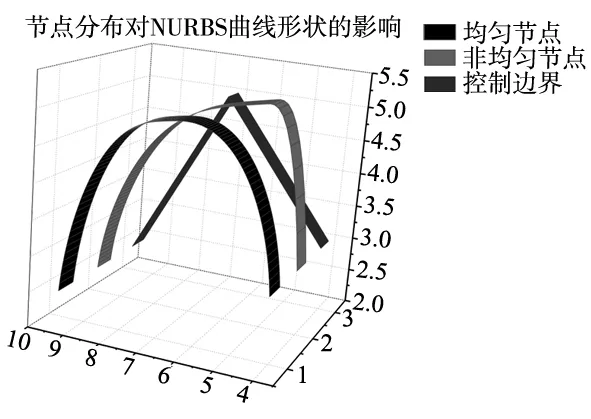
图1 节点分布对NURBS曲线形状的影响
针对于控制点权重带来的影响,控制变量仅修改夹角处控制点的权重观察NURBS曲线的形状,如图2所示,可知权重越大拟合曲线越逼近控制点,但同时曲线最大曲率增大。

图2 权重对NURBS曲线形状的影响
由性质(4)可知,对于3阶NURBS曲线,若要最终平滑路径平滑经过起点与终点,则需保证式(3)的成立。
(3)
1.2 局部轨迹平滑模型建立
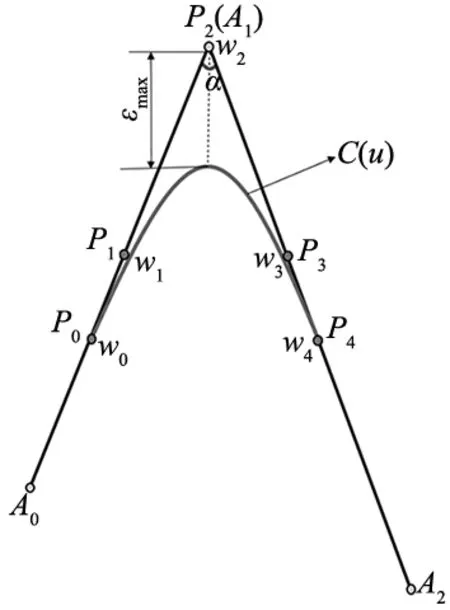
图3 轨迹控制边界与 局部平滑曲线
局部轨迹平滑对三个轨迹控制点形成的折线段进行平滑,分别记为A0、A1和A2。考虑到局部平滑之间应该具有隔离性,不能影响到下一段或者上一段的平滑,因此限制平滑后的NURBS曲线控制边界长度小于等于轨迹控制点构成折线夹角最小段的一半长度。故在轨迹控制边界上插入新的NURBS曲线控制点,分别记为P0、P1、P2、P3和P4,从而可通过限制控制点的坐标限制NURBS曲线的范围。此外,由图1可知,当曲线保持关于角平分线对称分布时,可以在具有相同误差时可保证最大曲率最小。因此P2与A1重合,如图3所示。
图中,C(u)为目标生成的平滑后的NURBS曲线。由于该曲线成对称分布,因此需要保证NURBS曲线控制节点权重对应相等,如式(4)所示。
(4)
此外,由图3可知此时控制点个数n为4,故可计算得到m的值为8,再由图1知,对称的NURBS曲线需要保持u节点区间均匀分布。结合式(3)可确定节点U分布如式(5)所示。
U=[0,0,0,0,0.5,1,1,1,1]
(5)
为了保证后续的全局平滑可以顺利拼接局部平滑的结果,因此需要限制NURBS曲线控制边界的长度,约束条件如式(6)所示。
(6)
在满足上述约束条件之后,则可以保证在NURBS曲线内部任意节点具有G2连续性。但对于曲线的端点来说,NURBS曲线只能保证与NURBS控制边界相切,即为G1连续,不能保证G2连续,故需要在边界处添加G2连续约束条件,如式(7)所示。
(7)
根据式(1)中NURBS曲线表达式可求得式(7)中的导数,如式(8)和式(9)所示。
(8)
(9)
将已知条件代入式(8)及式(9)之中,得到二阶导数如式(10)和式(11)所示。
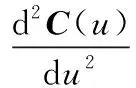
(10)
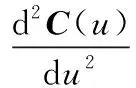
(11)
将式(10)、式(11)代入式(7)、式(8)中,可得G2连续的约束条件:
(12)
由NURBS曲线对称性条件及式(4)、式(6),可知此时只需要化简一个约束条件即可。为使得化简过程更为明确,将局部平滑中涉及到的NURSB曲线控制边界长度设定为如式(13)中所示的变量。
(13)
此外,对式(12)中相关向量使用单位向量进行进一步简化表示,减小等式中变量的个数,见式(14)。
(14)
将式(14)代入式(12)中,可得:
2w0(C1+le1)-3w1(C1+l2e1)+w2C1=0
(15)
化简式(15),合并相同的项之后如式(16)所示。
(2w0-3w1+w2)C1=(3w1l2-2w0l)e1
(16)
由式(16)可知,由于C1和e1方向不同,且上式需要保证在任意条件下需成立,所以此时两个向量的系数均为0,可将式(16)简化为式(17)所示。
(17)
经过上述计算,NURBS曲线一方面可以保证关于轨迹控制边界角平分线对称分布,并且在曲线上任一点均满足G2连续性,另一方面可以保证局部平滑的隔离性。
对于局部平滑的约束条件,即为在满足工艺要求轨迹误差约束的前提下取得最小的曲率,因此设定最终目标函数如式(18)所示。
(18)
式中,ρmax为NURBS曲线所有节点中最大的曲率。由于此时NURBS曲线满足轴对称性,可知曲率最大处即为u=0.5时对应的曲率,计算公式如式(19)~式(21)所示。
(19)
(20)
(21)
由于NURBS曲线此时满足轴对称性,所以εmax为u=0.5时对应的曲线误差,计算公式如式(22)所示。
(22)
将C(u)|u=0.5代入式(1),化简之后可得εmax如式(23)所示。
(23)
建立好数学模型的约束条件以及目标函数之后,则需要求解得到最优解。
1.3 Q-Learning求解
Q-Learning是一种强化学习算法,可用于在设定好的学习规则下学习探索到任意目标个数下的最优解,是一种无监督式地学习机制。
Q-Learning核心在于Q-Table的更新维护,Q-Table中每一个元素Q(s,a)表示在状态s的情况下,采取动作a获得的奖励大小,因此可以理解在Q-Learning在不断学习的过程,即为Q-Table的不断更新过程,并最终在Q-Table的引导下可以寻找到最优解。Q-Table的更新过程目标即为根据状态s′的值得到状态s的值的过程,其中更新公式[9]如式(24)所示。
Q(s,a)←Q(s,a)+α[R+γmaxxα′Q(s′,α′)-Q(s,a)]
(24)
式中,R为当前的奖励;Q(s,a)为上一个状态s′的Q-Table中状态s采取动作a获取到奖励的值,同时也作为下一个状态s的估计值;R+γmaxxα′Q(s′,α′)为状态s′时的Q-Table现实值;γ为对未来R衰减值;α为学习率,用于决定该次误差的学习程度。需要注意的是,在计算现实值时,每次以ε的概率选择Q表中的最大值对应的动作,1-ε的概率在Q表中随机选择动作,从而可以避免学习进入局部最优的情况。
根据以上Q-Learning算法的原理,可以搭建数学模型学习局部轨迹平滑中的最优解。使用曲率ρ的值来表示状态s,由于曲率ρ是一种范围连续变化的量,将之映射到离散状态s时使用值区间进行离散化,离散区间长度设为δ,故可表示如表1所示。

表1 曲率ρ到状态s映射表
对于动作a的映射来说,使用权重变化的方向作为采取的动作。由于此时权重的变化旨在对状态s的影响,故需要探索权重的3个自由度变化对曲率的影响关系。
由式(19)~式(21)可知,w0及w4对曲率的变化没有影响,故为验证该公式,并在保持NURBS曲线对称性不变的前提下,使用控制变量法分别修改权重为10,与原始权重均为1的情况下进行对比,得到结果如图4和图5所示。
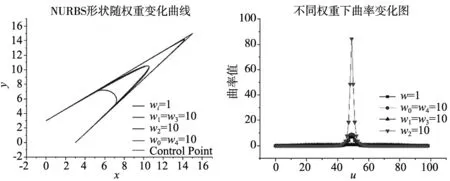
图4 NURBS形状随权重变化曲线 图5 不同权重下曲率变化图
此外,由于在权重的变化过程中仍需要满足式(17)的约束,故最终动作如表2所示。

表2 动作权重变化映射表

续表
对于Q-Learning的奖励函数,需要在学习的过程中抵触曲率变大以及最大误差变大的现象,因此奖励函数分为三部分,分别为曲率相对值的减小变化率、曲率减小绝对方向的变化率以及最大误差的绝对大小程度,具体如式(25)所示。
(25)
在完成上述的所有设定之后,则可以搭建好Q-Learning的算法模型,进行最终的训练学习。在最终结果的筛选中,由于为增大曲率变化的范围,并未设定严格的误差约束,因此在最终的学习结果中选择出满足误差约束的最小曲率对应的权重即可。
在得到最终所有控制点的权重之后,则可以根据式(13)、式(14)及式(17)计算得到所有控制点的位置,最终则可以计算出最终的NURBS曲线。
2 局部姿态方向角平滑
局部姿态方向角平滑是指在生成局部平滑轨迹的基础之上,根据轨迹曲率变化规划得到姿态方向角变化曲线的算法。由于在曲率较大的地方五轴混联机床各分运动部件速度变化骤烈,此时应尽量减小姿态方向角的变化速率来平滑分运动状态,以此为数学模型建立方向角的变化约束,并通过离散积分的方式获取最终的数值解。
2.1 数学模型建立
在五轴机床运动轨迹曲率较大处,运动状态变化剧烈,因此可通过减小此处的刀具姿态方向角变化速率来平滑机床的运动。为保证该约束的实现,建立姿态方向的约束模型,使得姿态方向变化率与曲率成反比,如式(26)所示,其中姿态方向向量记为o。
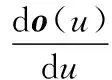
(26)
五轴机床的姿态方向是通过刀具路径不同控制点对应的三维方向矢量给定的,并且所有方向单位矢量均不共面,处于不同维度的圆锥之中,如图6所示。
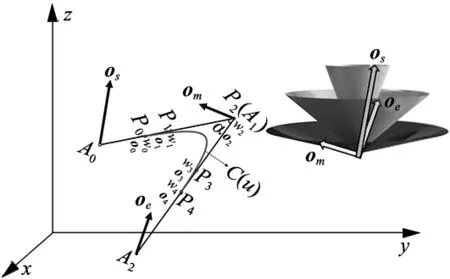
图6 不同控制点方向矢量
可以看出,所有的方向均处在不同的圆锥平面内,再加上直接对三维矢量进行平滑计算量大,因此使用分段的方法将之转化为一维变量,分别对图6中P0~P2段和P2~P4段进行平滑,即为将方向变化的信息提取为轨迹不同段方向向量之间的夹角α,因此方向变化率转为夹角α的变化率,此时约束如式(27)所示。
(27)
为保证局部角度平滑之间的隔离性,即为本段角度平滑结果不影响上一段及下一段的局部角度平滑,故设定在平滑轨迹的起点以及终点处的姿态方向角分别为A0、A2与A1角度的一半,如图7所示。
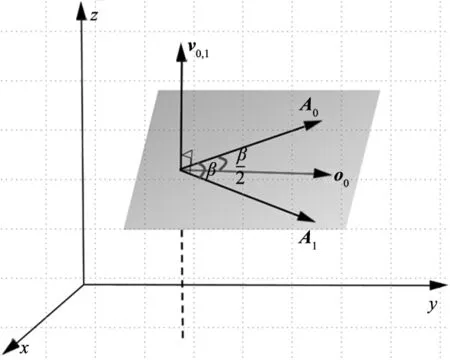
图7 角度平滑示意图
由于图7所有姿态方向矢量均为单位向量,故可建立边界条件如式(28)~式(30)所示。
(28)
o2=om
(29)
(30)
在建立求解条件以及约束条件之后,则可以对式(27)进行求解,然后反解得到姿态方向向量即可。
2.2 局部姿态方向角求解
式(27)拆分开包含变量u的函数,并进行对拆分后的整个积分可得式(31)。
(31)
代入式(21)计算得k的表达式,如式(32)所示。
(32)
式中,Δαi为分段平滑后的两个方向向量之间的夹角;u1、u2为分段后对应的u节点值,计算公式如式(33)~式(35)所示。
(33)
(34)
(35)
在计算得到k之后,代入式(32)中,将该积分形式进行离散化,可解得不同u对应的α的值。由于此时NURBS曲线成轴对称形状,故此时一个使用通式表示最终结果,如式(36)所示。
(36)
在得到α(u)之后,可通过反解计算得到不同u对应的姿态方向向量,设a为分段内的起始姿态向量,b为分段内的终止姿态向量,c为垂直于a、b的向量,因此可以通过两者的叉乘得到,αu为目标向量与a的夹角,α为a、b的夹角,ou为αu通过反解得到的最终目标向量。由上述约束条件可建立关于目标向量的三元一次方程组,如式(37)所示。
(37)
根据式(37)解得不同u对应的姿态矢量,并且满足局部的隔离性及局部运动平滑性。
3 全局平滑
在局部平滑中,由于考虑到每一段的隔离性,因此全局平滑即为在局部平滑的基础上,完成局部衔接段之间的拼接即可。
3.1 全局轨迹平滑
由于局部轨迹平滑时已经满足隔离性的约束,因此只需要添加衔接段将局部平滑轨迹连接即可。对于衔接段来说,由于式(7)的约束,可知局部平滑轨迹在端点处均与控制边界线段满足G2连续。此外,由于式(6)的约束,保证了局部平滑轨迹之间满足相互隔离性,因此可以直接将轨迹使用控制边界进行拼接即可,具体流程如图8所示。
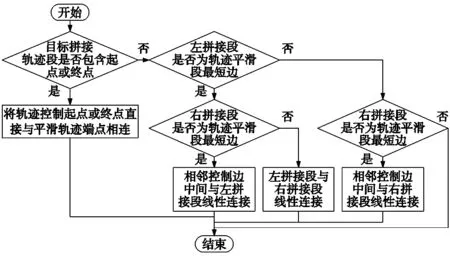
图8 全局轨迹平滑流程
3.2 全局姿态方向角平滑
局部角度平滑的结果中包含角度的隔离性约束,并且每段平滑角度的起点均为一条控制轨迹边端点姿态矢量夹角的一半,因此在拼接时满足角度的连续性。此外,对于起点以及终点到角度平滑段之间,由于此时轨迹为一段线段,因此使用线性插值的方法进行两端的角度平滑,如式(38)所示。

(38)
式中,i=0为起点段,i=1为终点段;α0为轨迹控制起点与局部NURBS轨迹控制起点之间的姿态矢量夹角;L0为其距离;α1为轨迹控制终点与局部NURBS轨迹控制终点之间的姿态矢量夹角;L1为其距离。全局姿态方向角平滑流程如图9所示。
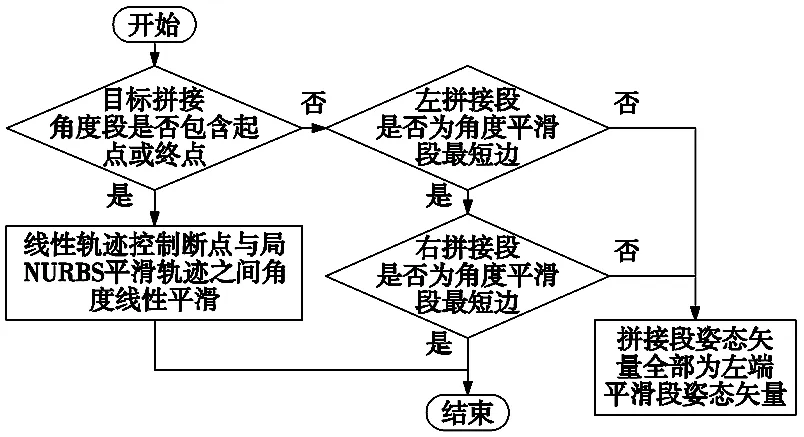
图9 全局姿态方向角平滑流程
在完成全局轨迹平滑及全局姿态方向角平滑之后,可以得到一条满足误差要求、曲率小、G2连续且近似为零件形状的加工路径。
4 仿真验证
在完成路径平滑算法之后,生成一条满足G2连续的光滑加工曲线,为验证算法的有效性,分别对算法的每一个环节进行计算。
4.1 局部平滑验证
设定Q-Learning学习率为0.1,奖励衰减因子为0.9,针对当前状态选择最优动作的概率为0.9,最大迭代次数设定为9000,奖励值中曲率相对值的减小变化率权重因子为100,曲率减小绝对方向的变化率权重因子为0.01,最大误差的绝对大小程度权重因子为1.0。对于零件形状控制轨迹来说,控制点坐标分别为(1.0,1.0)、(7.0,5.0)、(15.0,-3.0),控制点姿态矢量分别为(0.675 69,0.193 47,0.711 345)、(0.418 283,0.553 792,0.719 968)、(0.800 974,0.432 059,0.414 446),初始权重分别为100.0、200.0、400.0、200.0、100.0,曲线拟合最大误差设定为0.7 mm,使用Q-Learning算法型学习,结果如图10、图11所示。
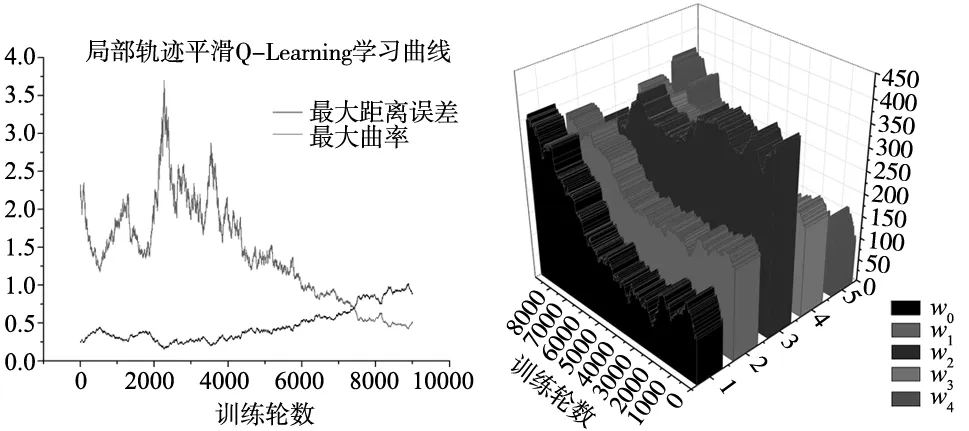
图10 局部轨迹平滑 Q-Learning学习曲线 图11 Q-learning权重 学习曲线
通过Q-Learning学习,最终选择的权重分别为250.0、291.0、373.0、291.0、250.0,从而可以根据式(13)、式(14)及式(17)计算得到局部平滑的轨迹,如图12所示。
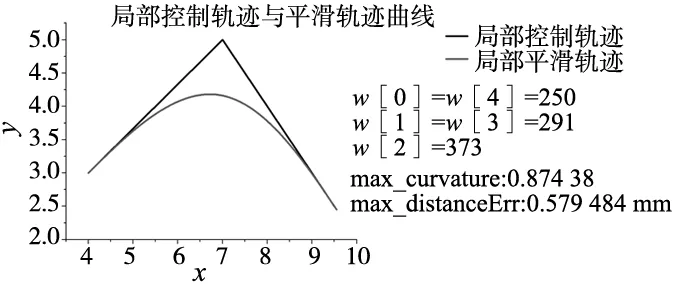
图12 局部控制轨迹与局部平滑轨迹曲线
图12中NURBS曲线保证局部轨迹的G2连续性,且最终最大误差为0.579 484 mm,小于误差约束0.7 mm,故该局部平滑结果满足要求。
在局部平滑轨迹曲线的基础上,计算得到不同u节点处对应的曲率,从而根据局部姿态方向角平滑可以计算得到不同曲率处的姿态方向角,如图13所示。
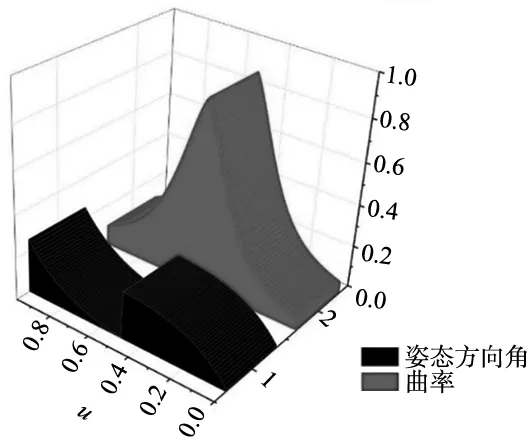
图13 局部角度平滑姿态方向角与曲率关系曲线
由图13可知,随着局部平滑轨迹曲率的增大,姿态方向角变化率会不断的减小,满足约束要求,姿态方向角变化率与曲率乘积得到的k值如图14所示。
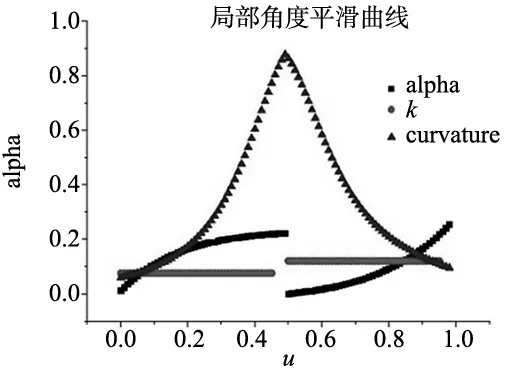
图14 局部角度平滑结果曲线
将平滑后的姿态方向角代入式(37),解得刀具不同平滑轨迹点对应的姿态方向矢量,如图15所示。
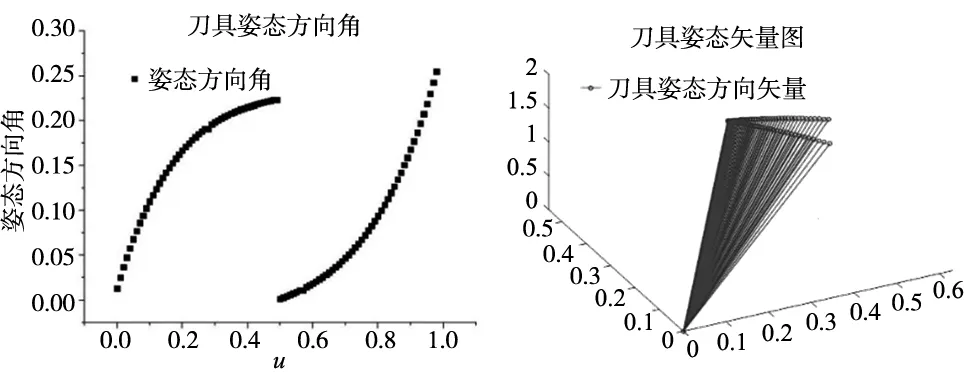
(a) 刀具姿态方向角 (b) 刀具姿态矢量图
综合局部刀具平滑轨迹以及平滑姿态方向矢量,计算得到最终刀具局部平滑路径图,如图16所示。
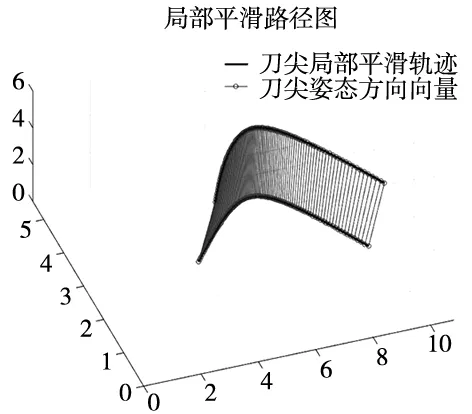
图16 局部平滑路径图
4.2 全局平滑验证
全局平滑即为在生成的局部平滑路径的基础上,完成局部段平滑拼接。设定加工零件的全局轨迹控制点坐标分别为(1.0,1.0)、(7.0,5.0)、(15.0,-3.0)、(25.0,-4.0)、(32.0,12.0)、(3.0,16.0)、(20.0,28.0)、(36.0,30.0)、(54.0,24.0),以及每个控制点对应的姿态方向矢量为(0.179 106,0.480 213,0.858 671)、(0.343 522,0.408 874,0.845 467)、(0.273 394,0.447 006,0.851 729)、(0.261 872,0.897 082,0.355 904)、(0.298 597,0.065 994,0.952 095)、(0.096 124,0.103 671,0.989 956)、(0.686 579,0.238 301,0.686 893)、(0.798 398,0.337 603,0.498 583)、(0.202 378,0.615 025,0.762 094),依次对每一个局部轨迹段使用Q-Learning进行权重学习,各个局部段轨迹形状学习过程如图17所示。
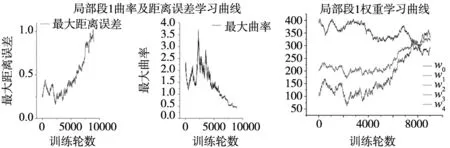
(a) 局部段1学习曲线
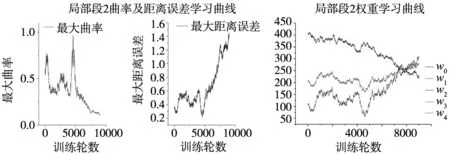
(b) 局部段2学习曲线
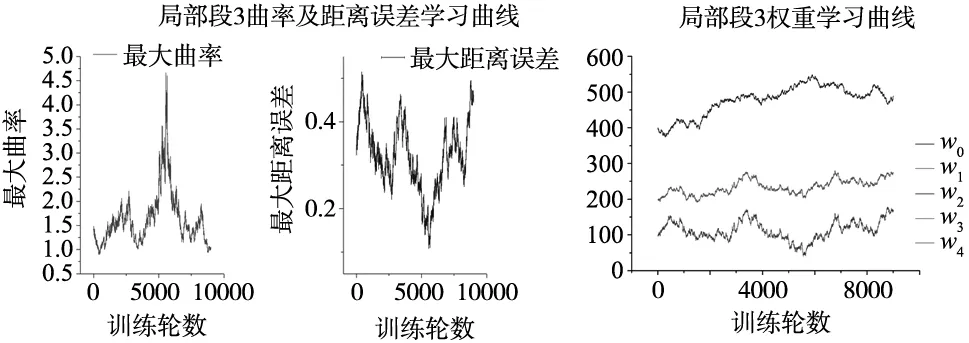
(c) 局部段3学习曲线
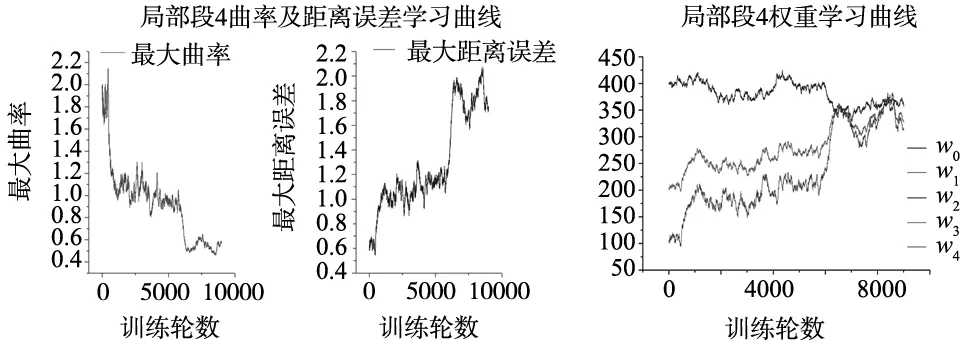
(d) 局部段4学习曲线
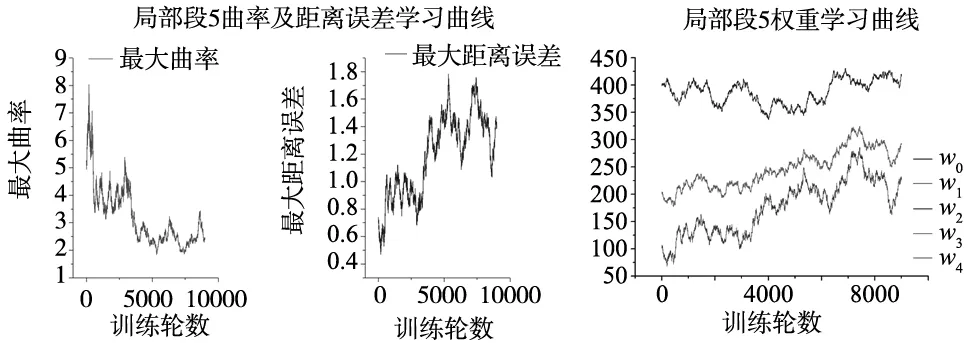
(e) 局部段5学习曲线
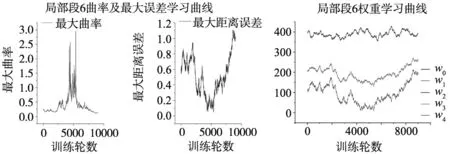
(f) 局部段6学习曲线
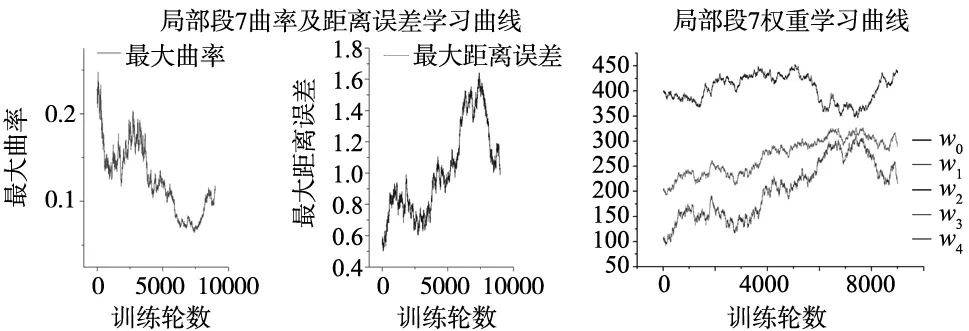
(g) 局部段7学习曲线
在完成各局部段的轨迹学习之后,则可通过全局平滑算法实现各个隔离局部段之间的平滑连接,最终得到全局平滑轨迹如图18所示。
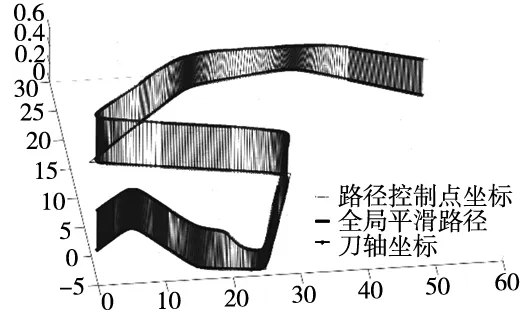
图18 全局轨迹平滑
由于在局部平滑中已经考虑到连续性问题、误差约束以及边界连续性问题,故最终平滑曲线同样满足约束条件。
5 结论
(1)综合考虑局部轨迹平滑段之间的G2连续性要求、隔离约束、误差约束,建立局部轨迹数学模型,设定减小曲率及轨迹误差为目标函数,通过Q-Learning学习得到满足目标函数的最优解。
(2)考虑局部平滑轨迹曲率与姿态方向变化率的关系,将三维方向向量转化为一维共面向量夹角,建立数学模型,通过离散积分求解方程,从而反解计算得到姿态方向矢量。
(3)结合局部的隔离性约束,实现各局部段的平滑拼接,生成刀具加工零件的平滑路径。
