面向UAV的绳驱动空中机械臂动力学建模分析*

2022-04-26梁栋，丁力，黄明，曹杰

组合机床与自动化加工技术 2022年4期

梁栋，丁力，黄明，曹杰

(1.江苏理工学院机械工程学院，常州 213000；2.南京航空航天大学机电学院，南京 210016)

0 引言

随着机器人工程、人工智能、传感器与通信等学科的发展，空中机器人在军民用领域得到了广泛应用[1-2]。但上述应用仍停留在被动作用阶段，近年来学者们更希望其能对所处环境施加主动影响，实现与环境的交互作业[3]。空中机械臂是一种由旋翼飞行器加装机械臂组成的新型系统，它能替代人完成高危环境下的信息采集、仪器远程操控等任务。因此，面向(unmanned aerial vehicle，UAV)的空中机械臂在一定程度上拓展了空中机器人的应用范围。

对于空中机械臂动力学建模的研究，国内外不少学者进行了一定的探索。张广玉等[4]设计了一款由6旋翼飞行器加装7自由度机械臂的空中机械臂，并将其当作质量分布随机械臂运动而变化的特殊系统，采用质点系的动量与动量矩定理对其进行了系统建模。ORSAG 等[5]将双机械臂加装到4旋翼飞行器上，通过分析悬停状态下机械臂与飞行器之间的力/力矩的内在联系，分别采用牛顿-欧拉法对两个子系统进行了建模分析。TOMASZ等[6]将具有展开式结构的轻质机械臂加装到无人直升机上，采用拉格朗日法给出了系统广义力与广义力矩的解析式。目前，大多数空中机械臂仍采用关节直驱方式，即将驱动电机、减速器及传感器直接安装在关节处，这不仅会增加臂身惯量，加重旋翼飞行机器与机械臂之间的耦合效应，还会限制机械臂自由度的增加，缩小了机械臂的操作空间。因此，研究空中机械臂的新型驱动方式具有一定的研究意义。

绳驱动技术将驱动模块外置，有效降低了系统特定部分的体积与惯量、增加了机械臂的柔顺性，有利于提升系统在复杂非结构环境中的作业能力与适应能力。考虑到绳驱动技术低摩擦、低惯量、零回程间隙等特性，ROOKS[7]研制了一款绳驱动拟人机械臂WAM，实现了与作业环境全方位安全交互。DE等[8]设计的套轮式绳驱动机械臂Dexter可实现各关节运动完全解耦，便于机械臂控制器设计及关节数目的叠加。在此基础上，本课题组进一步研究了绳驱动机械臂的结构设计[9]、运动学主动解耦机理[10]、轨迹跟踪控制[11]等内容。

为分析绳驱动空中机械臂的动力学特性，本文对绳驱动空中机械臂的机体、机械臂及绳索机构进行了三维建模。进而，将整个系统分为4旋翼飞行器和机械臂两个子系统，综合牛顿-欧拉法、旋量理论、拉格朗日法和空间算子代数(spatial operator algebra，SOA)理论推导出了两个子系统的运动学和动力学。最后，分别在MATLAB和Adams仿真环境下对绳驱动空中机械臂的运动性能进行了模拟分析。

1 机械设计

本文设计的面向UAV的绳驱动空中机械臂虚拟样机如图1所示，包括4旋翼飞行器和二自由度绳驱动机械臂。飞行器上装有4个桨叶及电机、2个GPS模块、1个Pixhawk飞行控制器和起落架。飞行器下方设计有2层挂板，上层安装一块6 s锂电池，下层用来安装直流减速电机以及挂载绳驱动机械臂。飞行器和机械臂的控制器是独立的，即前者用机载Pixhawk飞行控制器，后者用Stm32控制板。飞行数据与机械臂响应数据可通过机载SD卡储存或经数传实时发送至地面站。

图1 面向UAV的绳驱动空中机械臂虚拟样机

绳驱动机械臂具有2个平行关节，如图2所示。2套直流减速电机被安装在基座处，下方电机通过驱动轮上缠绕的两根绳索驱动大臂关节1正反转，上方电机通过主动轮、导向轮及张紧轮将力矩传递到小臂关节2处，最终实现末端执行器的给定运动。另外，两根关节轴上分别安装了编码器，用于测量关节角的信息。这样的设计可有效减轻臂身重量和关节惯量，提高末端负载自重比，同时兼具结构轻巧、减振吸振的优点。

图2 绳驱动机械臂三维示意图

关节绳索的走线形式如图3所示，其中直流减速电机拉动绳索1实现关节轮的正转、拉动绳索2实现关节轮的反转，这样便实现了关节驱动的解耦。同时，张紧机构中的张紧轮提供预紧力，保证电机力矩传递的可靠性。导向轮可改变绳索方向，使得两个关节的绳索互不干涉。

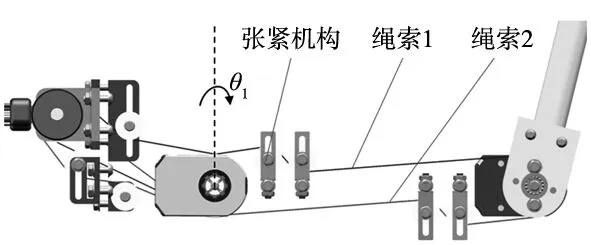
图3 绳索走线形式

2 系统模型

如图4所示，对于绳驱动机械臂的描述需要3套坐标系，即惯性坐标系{I}、机身坐标系{B}和机械臂坐标系{1}、{2}及{e}。

图4 绳驱动机械臂机构简图

这里需要强调的是本文讨论的系统建模仅触及到多刚体建模理论，为了简化建模过程，故不考虑4旋翼和机械臂之间的动力学耦合效应、绳索柔性变形、关节摩擦间隙及空气阻力等非线性因素。

2.1 4旋翼系统模型

将4旋翼看作一个单刚体，其动力学模型可由牛顿-欧拉方程[12]获得：

(1)

式中，IP∈R3和IV∈R3分别为4旋翼在坐标系{I}下的位置和线速度；g为重力加速度；f为总拉力；m0为4旋翼质量；Θ∈R3和Bω∈R3分别为在坐标系{B}下的欧拉角和角速度；J∈R3×3为转动惯量；τq∈R3为桨叶在机身轴上产生的力矩，包括横滚力矩、俯仰力矩及偏航力矩；R和W分别为转换矩阵，即：

(2)

(3)

式中，s(·)和c(·)分别是sin(·)和cos(·)的缩写；φ是横滚角；θ是俯仰角；ψ是偏航角。

对于X字型的4旋翼来说，总拉力、力矩与桨叶转速之间的数学关系为：

(4)

式中，cT、cM和ωi(i=1,2,3,4)分别为桨叶升力系数、反力矩系数和转速。

2.2 机械臂运动学模型

绳驱动机械臂运动学模型可构建在指数积公式的基础上[13]，故其正向运动学方程为：

(5)

(6)

式中，ωi、vi分别为第i关节的角速度和线速度；S(·)∈so(3)为反对称矩阵。

表1给出了绳驱动机械臂在基坐标系下的旋量参数。

表1 基座标系的旋量参数

根据表中参数可以很容易计算出末端执行器在基坐标系下的位姿，这里就不再给出详细的计算步骤。

进而，可通过如下齐次变换矩阵BU1将坐标系{e}中的位姿投影到机身坐标系{B}中，即：

BTe=BU1T

(7)

根据正向运动学的结果，可求出机械臂反向运动学的解析解，即：

(8)

2.3 机械臂动力学模型

绳驱动机械臂的反向动力学模型可由拉格朗日方程推导获得，即：

(9)

式中，L为拉格朗日函数；Ki和Pi分别为第i根连杆的动能与势能。这里需说明的是本文将连杆质量集中到关节处。

可将上述模型改写成反向动力学方程的一般形式，即：

(10)

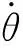
对于绳驱动机械臂正向运动学求解，由于计算质量矩阵M(θ)的逆耗时费力，故采用SOA理论来解决这一问题，即利用Kalman滤波平滑法将M(θ)分解成如下形式：

M(θ)=(I+HΦU)D(I+HΦU)T

(11)

其逆矩阵为：

M(θ)-1=(I-HΦU)TD-1(I-HΦU)

(12)

式中，H为状态转换算子；Φ为空间移位算子；U为Kalman移位算子；D为关节空间中关节无记忆质量算子。定义其他SOA算子，即Q为状态空间中关节无记忆质量算子；B为Kalman增益算子；Λ为机械臂算子。这些算子的具体解释可参考课题组前期研究成果[14]，这里就不再赘述。

若已知关节力矩τm，则基于SOA理论的绳驱动机械臂高效率正向动力学递推公式为：

(13)

进而，对关节加速度进行积分便可获得关节角速度和关节角。

3 仿真分析

为了深入剖析面向UAV的绳驱动空中机械臂的运动特性，本节通过3个仿真算例来演示说明。表2给出了仿真中绳驱动空中机械臂的物理参数。

表2 绳驱动空中机械臂的物理参数

(1)4旋翼飞行轨迹仿真。在0～5 s内，机械臂相对4旋翼保持静止，飞行器从原点飞至(8 m,10 m,-12 m)的目标位置悬停，其他初始条件均为0。过程中，4旋翼的力矩信号由串级PID控制器生成，这里就不再扩展说明，详细过程可参考文献[15]。仿真结果如图5～图8所示，可以看出4旋翼可在4 s左右到达目标位置，位置和姿态变化较为平坦，力矩响应速度也较快，这说明了本文建立的4旋翼系统模型是合理正确的。

图5 4旋翼三维飞行轨迹图6 4旋翼三轴位置变化曲线

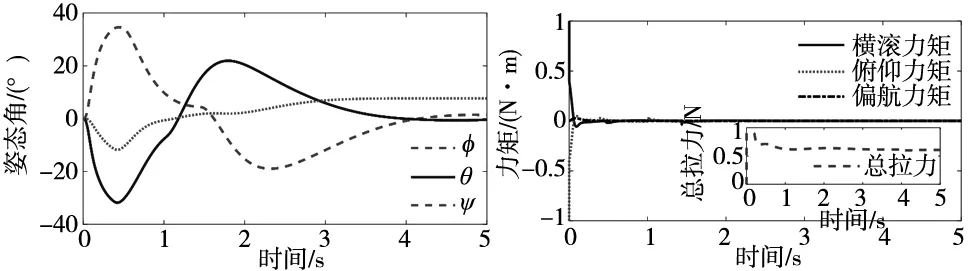
图7 4旋翼三轴姿态变化曲线图8 4旋翼力矩变化曲线

(2)机械臂反向动力学仿真。在2 s内，驱动绳驱动机械臂的关节角θ1从-30°变化至20°，关节角θ2从-60°变化至60°。采用五次多项式规划出两关节在2 s内的关节角、关节角速度及关节角加速度的变化历程，如图9所示。根据式(5)～式(7)计算出末端执行器在机身坐标系{B}下的位置变化，如图10所示。利用式(10)计算出此变化过程所需的关节力矩，结果如图11所示。上述结果进一步说明了利用旋量理论和拉格朗日法建立机械臂运动学模型和反向动力学模型的可行性。

图9 关节空间轨迹规划结果

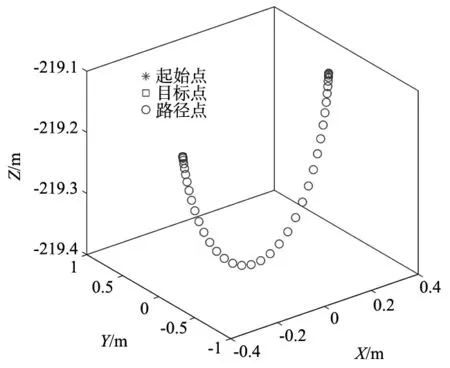
图10 机身坐标系下末端执行器位置变化

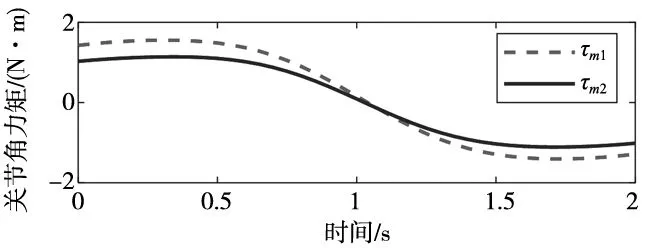
图11 关节力矩变化曲线

(3)机械臂正向动力学仿真。设计两个关节角力矩信号为τm1=sin(t)，τm2=cos(t)，仿真时间为2 s。为了验证基于SOA理论的绳驱动机械臂高效率正向动力学递推公式的有效性，将绳驱动空中机械臂的三维模型导入到ADAMS软件中，并在软件中给两个关节添加同样的驱动力矩。数值仿真与软件模拟的结果如图12所示。从图中可以看出，经基于SOA理论的绳驱动机械臂高效率正向动力学递推算法获得关节角理论曲线和在ADAMS软件中仿真得到的曲线几乎一致，这说明本文所提正向动力学建模方法的有效性。