火星探测器大气数据测量方法

2022-04-26陈广强豆国辉魏昊功邹昕李齐刘周周伟江

航空学报 2022年3期

陈广强，豆国辉,*，魏昊功，邹昕，李齐，刘周，周伟江

1.中国航天空气动力技术研究院，北京 100074 2.北京空间飞行器总体设计部，北京 100094

嵌入式大气数据传感(Flush Air Data Sensing, FADS)系统依靠压力传感器阵列测量飞行器表面的压力分布，通过特定算法间接获得动压、总压、攻角、侧滑角等大气数据。FADS已经成功运用到美国X-15、F/A-18、X-31、X-33、X-34、X-38、X-43A和航天飞机等多种类型飞行器。世界其他航空强国也都在各种飞行器上开展FADS技术研究。日本在20世纪90年代，通过高超声速飞行试验(HYFLEX)计划开展了FADS研究。欧洲防务公司EADS对FADS系统开展大量研究，现已开发成熟产品。

关于FADS技术国内也开展了大量研究。早在2004年,南京航空航天大学张斌与于盛林就开展了嵌入式飞行参数传感系统的设计与可行性验证研究，提出了使用BP神经网络来代替嵌入式飞行数据传感系统的空气动力学模型。南京航空航天大学陆宇平教授等针对算法、校准，系统误差、标定、FADS与INS组合技术和故障检测等多个方面开展了FADS技术全面研究，为国内FADS技术发展做出重要贡献。西北工业大学李清东、郭阳明等探讨了FADS快速智能故障检测和诊断技术。华中科技大学高隆隆等通过建立管路终端负载为容腔的测压管内气体压力传递数学模型,研究嵌入式大气数据传感(FADS)系统测压管路动态响应特性。沈阳飞机设计研究所王岩和郑伟针对航空歼击机的分布嵌入式大气数据系统算法开展初步研究。空军工程大学工程学院江城等开展嵌入式大气数据系统神经网络算法仿真研究。2010年以后,FADS技术得到迅速发展，中国空气动力研究与发展中心李其畅等分析了嵌入式大气数据三点解算方法的可行性，介绍了嵌入式大气数据受感系统设计的基本准则以及理论分析与风洞试验相结合的方法。南京航空航天大学张铭格开展高超声速嵌入式大气数据传感系统及研究。西北工业大学陈康等针对不同布局下高超声速飞行器开展FADS求解精度研究。孟博等开展基于神经网络的类乘波体飞行器FADS算法研究。航空工业成都凯天电子股份有限公司熊亮等针对武装直升机大气数据传感器技术分析了研究进展。中国航天空气动力技术研究院在FADS理论、风洞验证和飞行试验测试等方面开展了工程应用研究。相对于国外已经比较成熟的FADS 技术而言，国内对FADS 技术的研究起步较晚但技术发展迅猛，特别是近5年取得巨大进步，FADS系统目前已经成功应用到中国的歼20和运20等先进武器装备上。

相比之下火星大气数据测量技术研究非常少，国内北京空间技术研制试验中心杨雷等开展火星探测器进入飞行气动测量方法研究，基于弹道重建和嵌入式大气数据传感系统，提出火星探测器进入飞行过程中的气动测量方法。通过融合火星进入外测弹道信息，利用输出误差法实现攻角、侧滑角的高精度测量；基于嵌入式大气数据传感系统，利用最小二乘最优估计算法，建立了进入飞行动压的测量方法。2012 年8 月5 日，美国航空航天局的“火星科学实验室”(Mars Science Laboratory, MSL)进入舱(Entry Vehicle, EV)成功进入火星大气层、并在火星表面盖尔环形山(Gale Crate)位置安全着陆,实现了人类首次对火星大气数据的近距离测量研究。图1所示为MSL嵌入式大气数据传感系统，也称为火星进入大气数据系统(Mars Entry Atmospheric Data System,MEADS)。

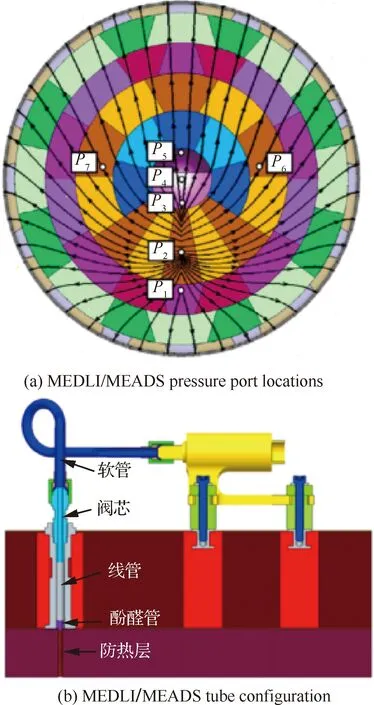
图1 MSL嵌入式大气数据系统[1]Fig.1 MSL Mars entry atmospheric data system[1]

火星大气非常稀薄，密度只有地球的1%左右。火星大气的主要成分为二氧化碳和氮气等，而且经常有沙尘暴。火星表面温度白天最高可达28 ℃，夜晚则降低到-132 ℃，平均-57 ℃。虽然二氧化碳含量是地球的几倍，但因缺乏水汽，所以温室效应只有10 ℃，比地球的33 ℃低得多，对大气数据测量系统的软件和硬件设计产生很大影响。由于探测器在进入火星大气层的飞行弹道马赫数高达30，而到达近地面时马赫数接近2。飞行速域宽，出现马赫数无关性和化学非平衡反应效应等物理现象对火星大气数据测量算法建模造成很大困难。

本文针对某火星探测器开展进入飞行大气数据测量方法研究。提出了基于MEADS/IMU耦合的大气测量方法，利用自主研发CACFD软件平台的化学非平衡模型/完全气体模型计算获得探测器宽速域飞行流场的表面压力点数据建立了基于BP神经网络的算法模型，并完成了大气数据测量仿真分析和飞行试验数据分析。

1 火星探测器大气数据测量关键技术

火星探测器的着陆过程可分为4个阶段：接近段、大气进入段、降落伞减速段和动力下降段，其中将后3个阶段称为“进入(Entry)、下降(Descent)、着陆(Landing)”，简称为火星的“EDL”过程，如图2所示。在进入段过程MSL探测器的飞行马赫数范围约为2～30，动压范围约为0～16 kPa，配平攻角范围为-20°～0°，侧滑角范围为-5°～5°，如图3所示。

由于受到传感器性能限制只能测量部分飞行弹道，如MSL只能测量动压大于850 Pa的飞行弹道，为 60 km以下的连续流飞行速域。宽速域、高马赫数和复杂大气环境给火星探测器MEADS系统的设计带来诸多挑战，下面介绍火星探测器MEADS系统设计的4个关键技术点。

1) 关键技术点1

算法设计决定了整个系统的顶层设计方案。MEADS采用最小二乘法和卡尔曼滤波技术建模拟合表面7个测压孔数据获得飞行大气数据测量结果，建立压力分布模型来确定大气数据评估的最小偏差。

当与IMU单元结合时，MEADS可以用于测量风速和密度。MEADS建模评估攻角、侧滑角、动压和静压。最小二乘法模型与IMU耦合，即使用IMU速度校核MEADS测量的马赫数。大气密度以MEADS测量的动压和IMU测量的速度计算获得，假设无风速的影响。MEADS测量的动压和IMU测量的加速度和角速率还可以联合评估飞行器的气动力和力矩。利用卡尔曼滤波技术建模可以将MEADS和IMU测量的结果以紧密的方式耦合在一起，为了可以应用MEADS测量表面压力数据和IMU加速度和角速率数据直接计算大气状态变量和风速。该方面将压力模型重新写成大气来流参数(压力、密度和切向风)，以及探测器相对火星的速度和方向的函数。在计算这些转换的状态之后，气动力方位角、马赫数、动压作为计算结果输出。设计结果表明MEADS的攻角和侧滑角测量精度在弹道大部分区域均达到设计的目标，只有在低马赫数(Ma<5)区域攻角的测量精度大于0.5°。动压的测量精度在整个测量弹道均达到设计指标。马赫数测量精度的设计目标无法达到。MEADS算法建模对大气数据测量结果产生重要的影响,决定着测量数据的准确性和可靠性。因此大气数据测量的建模设计成为火星探测器MEADS设计的首个关键技术点。

图2 MSL进入、下降和着陆过程Fig.2 MSL entry, descent and landing process

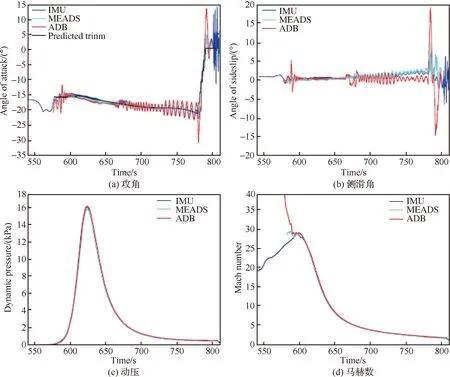
图3 MSL进入飞行弹道测量结果对比Fig.3 Comparison of MSL entry flight trajectory measurement results

2) 关键技术点2

基于数值模拟方式建立的气动压力数据库是MEADS算法设计的重要基础。MEADS算法建模设计需要大量气动压力数据作为支撑，但是火星探测的飞行数据稀缺，地面风洞试验验难度也很大，数值模拟成为获取火星探测器进入段气动数据的重要工具。

数值模拟是以计算流体力学为基础，对流体动力学方程、传热方程或其各种近似形式离散求解，能够模拟出探测器进入阶段的流动传热细节，较准确地预测出火星探测器进入大气层的气动力热环境和结构传热特性，经过飞行和风洞试验数据检验校正的数值模拟手段可以为MEADS设计提供基础的数据支撑。进入段火星探测器各个速域流场非常复杂，最典型的是在高马赫数段(=30～10)飞行时出现化学非平衡效应。在化学非平衡效应影响下，激波形状发生明显变化，将影响飞行器整体气动特性。驻点温度明显降低，波后温度明显不同，在飞行器后体的尾迹流动中出现大范围的低温区，是由强烈的化学反映所致，将影响探测器的气动力、热性能。如何准确模拟化学非平衡效应成为火星探测器MEADS设计的第2关键技术点。NASA在研制MSL大气数据测量系统的过程中，发展了一个基于CFD(Computational Fluid Dynamics)数据模型，该CFD数据库是基于对火星大气进入过程中的高超声速和超声速的飞行阶段，对进入舱流动进行N-S方程求解获得压力分布，Navier-Stokes(N-S)方程求解器采用薄层假设的NASA兰利中心的LAURA程序(Langley Aerothermal Upwind Relaxation Algorithm)，可预测化学非平衡效应。程序采用可变温度的CO分子松弛变量、Camac模型和7块单区网格对前体进行求解。利用化学非平衡方法和等效比热比方法结合还可以准确评估获得各速域条件下的热力学参数，为大气数据换算提供准确的比热比，对于提高大气参数测量精度具有重要的意义。

3) 关键技术点3

误差模型设计是控制系统误差的重要手段,根据误差源设计合理的误差模型有利于提高系统的精度。

MEADS系统的主要误差源有：① 测压孔位置误差，由于探测器是轴对称外形，可以将测压孔安装后的位置误差等效成经纬方向角度的随机扰动位置误差。火星科学实验室测压点的位置精度为0.05英寸(1.27 mm)(3)，由于火星科学实验室的直径达到4.5 m，而且大底表面布满隔热瓦，测压孔是安装在隔热瓦对接的缝隙中，该位置精度对制造安装工艺要求还是相当苛刻的。② 传感器测量误差，现有地球飞行器FADS系统的压力传感器测量误差通常要求≤0.05%FS(全量程)，由于火星科学实验室MEADS系统测量范围大，因此需要精度更高。③ 时间误差：不同测压孔的遥测时间一致性的相对误差产生的压力误差，引发MEADS算法求解结果的失真。包括系统的和随机的时间误差，系统误差可以通过调整飞行数据预处理方法而消除，而随机的误差则无法消除，火星科学实验室每个测压孔取随机的时间误差为±25 μs，必须将随机的时间误差加到真实测量的结果中计算测量的压力。④ 热辐射影响误差：在稀薄流动条件下，热传导引起管路内效应，使得传感器压力与表面压力出现严重偏差。这种效应可以分为两个方面，一方面是由飞行器表面与传感器的温度梯度造成的，另一方面则是由热传导/剪切应力引起的。⑤ 系统校准和温度不确定性误差。⑥ IMU测量误差。误差模型是根据MEADS系统设计目标，结合误差源对各个误差进行合理分配而建立的数学模型，误差模型设计需要考虑多方面因素的影响。对误差源的误差影响必须进行科学评估，如果对各个误差源评估过高，则会造成分系统技术要求指标过严，该分系统可能无法完成设计或者成本急剧增加，评估过低则会造成MEADS系统设计测量精度指标无法达到而导致系统设计失败。

4) 关键技术点4

压力测量模块是MEADS获取表面压力数据的主要手段,是重要的硬件组成部分。进入段探测器表面气流温度可能超过1 200 ℃,取气装置和引气管路都应采用耐高温的材料和耐高温密封设计。同时作用于压力传感器的受感元件上的气体很可能也具有很高的温度,因此,需要通过冷却装置使管路中的气体温度能满足传感器工作条件。压力传感器不仅要求耐高温工作环境,还必须具备宽量程测压能力, 适应跨大空域的飞行特点。由于火星大气密度很低，测压管路延迟非常严重，对MEADS系统精度测量造成很大的影响，必须对管路延迟影响进行补偿。因此火星探测器MEADS系统需要设计高精度、抗高温、宽速域和低延迟的压力测量模块系统，成为火星探测器MEADS设计的第4个关键技术点。

2 化学非平衡数值模拟

2.1 数值模拟方法

火星大气高超声速黏性流场的高精度数值模拟对物理模型提出了很高的要求。对流场数值模拟和气动特性计算精度影响较大的主要有两个方面：① 高温条件下多组份火星大气输运属性的精确高效计算；② 热化学非平衡时振动能和平动能之间的松弛关系。本课题组针对火星探测工程项目已经发展和完善了可预测化学非平衡反应的CACFD软件平台。该平台针对火星大气进行计算时采用的是8组份化学反应模型(CO，CO，O，O，C，N，N，NO)，与NASA的LAURA软件一致，成功完成Phoenix火星探测器算例验证研究。目前CACFD软件平台已经开始应用于火星探测器气动设计与评估项目。针对高温条件下多组份火星大气输运属性的精确高效计算，本课题组对包括Wilke混合公式、Gupta-Yos混合公式和Armaly-Sutton混合公式在内的多种近似混合公式进行测试和评估，并最终选取了适合火星大气高超声速黏性流场模拟的方法。针对火星大气高超声速黏性流场的热化学非平衡计算，采用Camac松弛模型进行，并和Millikan-White松弛模型进行比较，分析了不同松弛模型对空间和表面流场模拟的影响。具体的化学反应方程如下：

热力学参量(如比热、焓等)，输运系数(如黏性系数μ、热传导系数、扩散系数等)，均通过温度拟合多项式得到。混合气体的对应参数由Wilke公式计算。化学反应源项通过有限速率化学反应模型得到，将化学反应写为

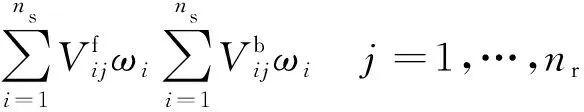
(1)

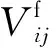
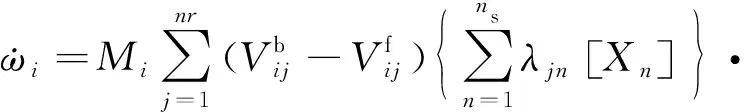
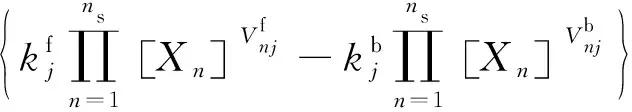
(2)

式中:、分别为第个反应的正向和逆向反应速率，可通过Arrhenius公式计算获得;是第个组份的摩尔分数;是组份摩尔质量;为三体系数。

正向化学反应速率公式：

=exp(-)

(3)

逆向化学反应速率通过平衡常数得到：

(4)

平衡常数可采用气体参数直接求得，也可以使用拟合公式得到，拟合公式为

=exp(+ln+++)

(5)

化学反应气体采用8组份(CO，CO，O，O，C，N，N，NO)、9个反应的化学反应动力学模型。具体反应类型如表1。

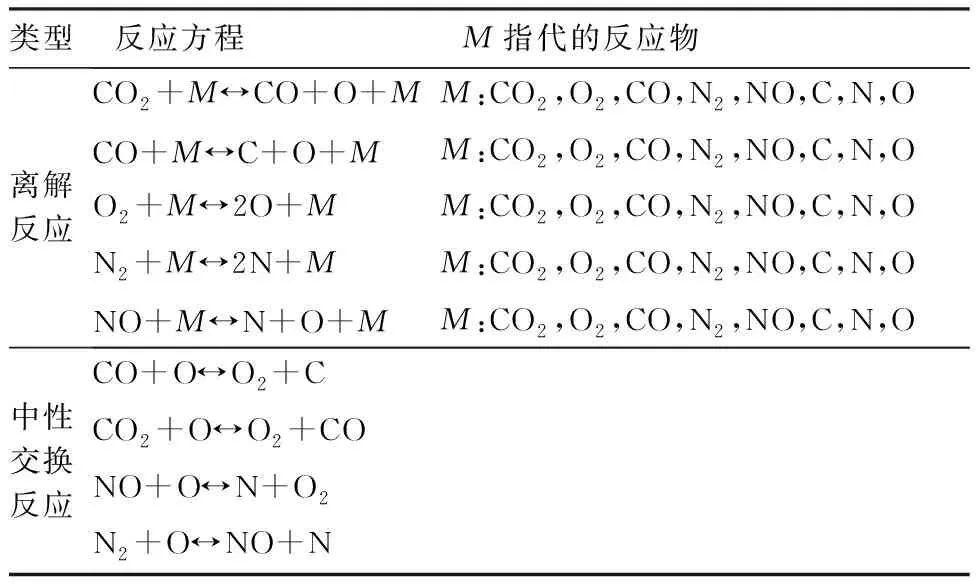
表1 火星大气化学非平衡模型化学反应类型

2.2 算例验证

本课题组所在的研究室已经开展了火星探测器气动计算数值模拟技术研究，并完成了相关项目的研究工作。建立了化学反应非平衡和等效比热比计算数值模拟方法。图4为文献[36]中给出的Phoenix几何尺寸与计算网格，该文在高超连续流区只针对Phoenix的前体进行了计算，因为文中认为后体对于整体气动力的贡献可以忽略。因此，在与文中数据进行对比时，同样选取的是探测器前体积分得到的气动力/力矩系数。文献[36]中采用的解算器是在MPF和MER上都得到过应用的软件LAURA。LAURA可预测非平衡化学效应，针对火星大气进行计算时同样采用的是8组份化学反应模型(CO，CO，O，O，C，N，N，NO)，与本文所使用的模型一致。

文献[36]给出了Phoenix高超声速范围静态气动特性不确定度，其中轴向力系数为±3%，法向力系数为±0.01，质心俯仰力矩系数为±0.002×[1.2, 0.8]。图5～图7即为本项目所采用的CACFD(GiAT)和NeqFRad两种软件平台通过化学非平衡模型计算得到的Phoenix气动特性曲线与文献[36]中LAURA给出的结果比较，包括、和zg(质心位置与文献一致，为=0.253，=0)。图中为攻角。总体而言，本项目的计算结果与LAURA的数据吻合得很好，其中最大偏差不超过0.9%，最大偏差约为0.002，zg最大偏差不超过 0.001。参照文献[36]中的数据，本项目软件平台与LAURA结果的偏差均在该不确定度范围内，表明本项目所采用的化学非平衡方法是准确与可靠的。

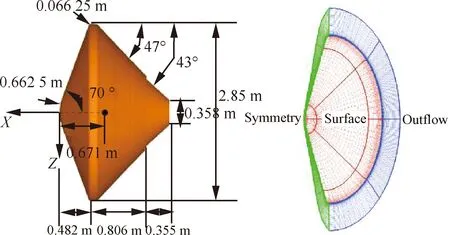
图4 Phoenix的几何尺寸与计算网格[36]Fig.4 Geometry and computational mesh of Phoenix[36]

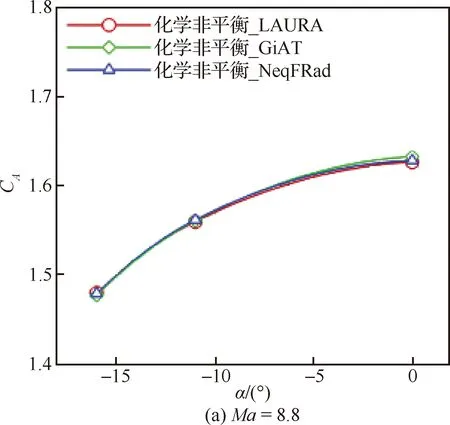
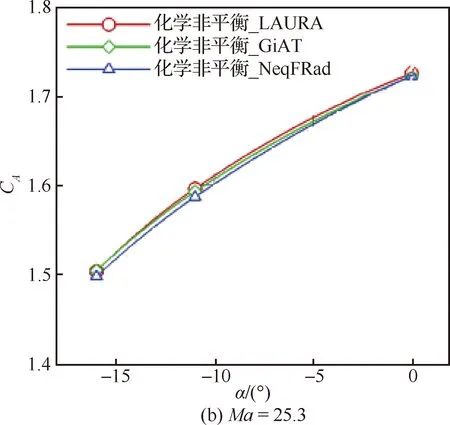
图5 不同求解器Phoenix轴向力系数对比Fig.5 Comparison of CA of Phoenix from different solvers

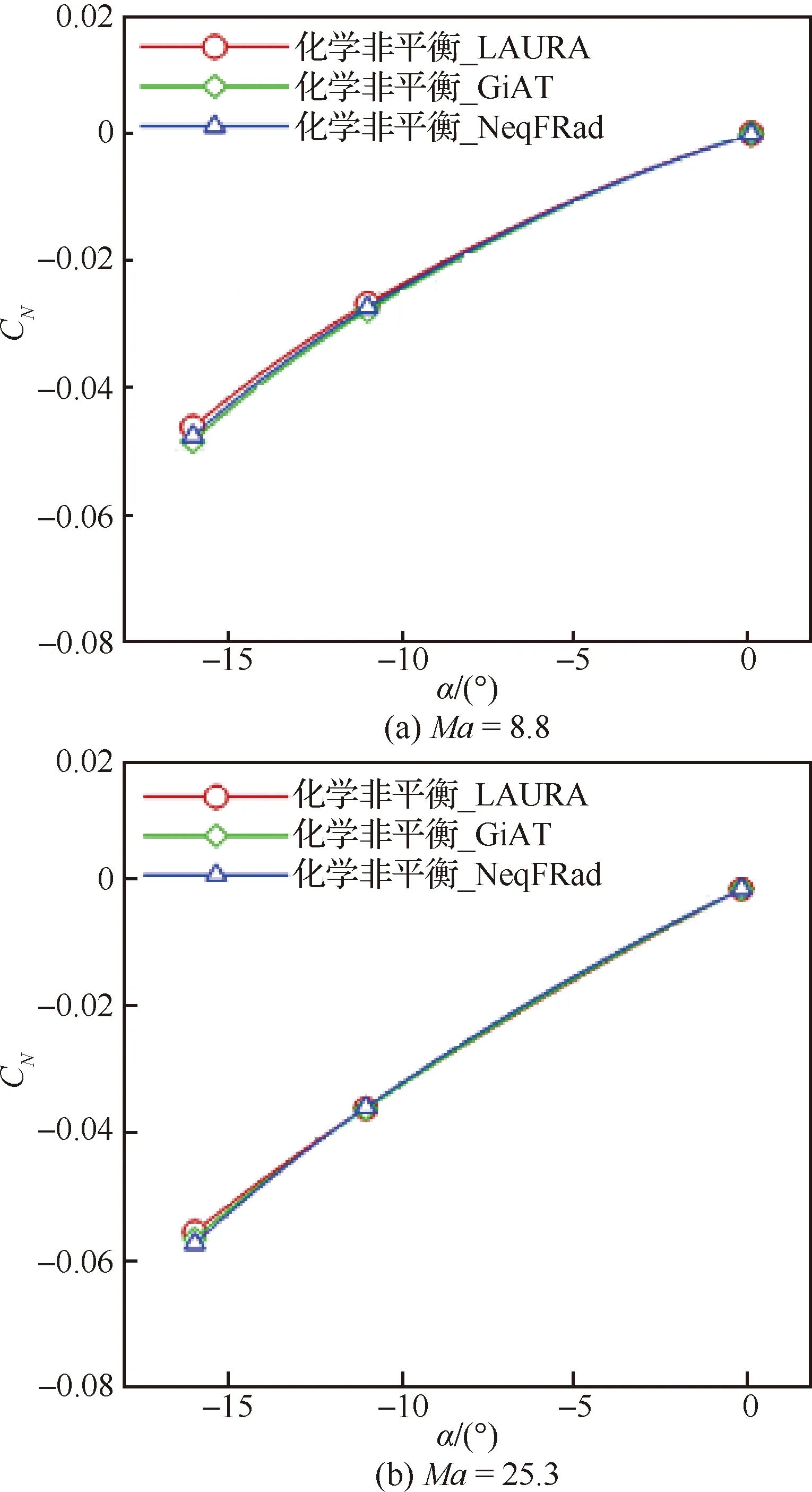
图6 不同求解器Phoenix法向力系数对比Fig.6 Comparison of CN of Phoenix from different solvers

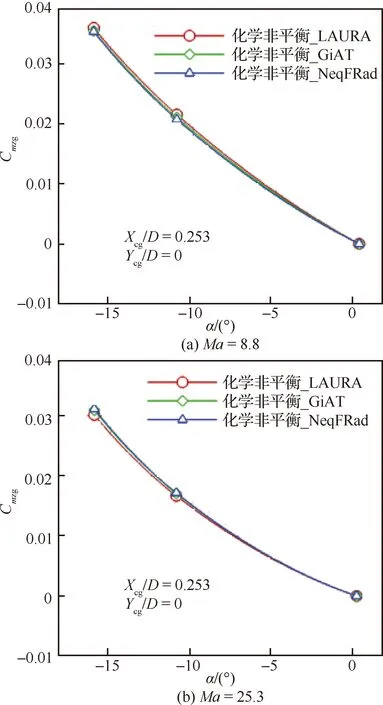
图7 不同求解器Phoenix质心俯仰力矩系数对比Fig.7 Comparison of Cmzg of Phoenix from different solvers

3 算法设计

计算流体力学立足于揭示探测器飞行流动机理，准确获取探测器表面流场数据信息。飞行大气数据测量建模着重于构建探测器飞行来流参数与探测器飞行流场数据的非线性映射关系。与传统地球大气数据测量研究建模相比，本文采用化学非平衡模型/完全气体模型的数值模拟计算，能更加准确模拟宽速域、高马赫数飞行流场结构，特别是飞行马赫数大于10以上产生的化学非平衡效应的影响，获得真实、准确的流场数据。再结合神经网络技术，利用其强大非线性映射能力，探索建立宽速域、高马赫数大气数据测量方法的求解模型。

3.1 基于BP神经网络的MEADS算法

BP(Back Propagation)神经网络是神经网络技术的基础，也是人工神经网络最精华的部分，它是一种采用误差反向传递的神经网络。BP网络的基本定理是：对给定的任意变量>0和任意的二阶连续函数():[0,1]→，则必然存在一个3层网络，它可以在任意平方误差精度内逼近(),即BP网络具有任意逼近一个二阶连续非线性函数的性能特点。正是利用这一特点建立基于BP神经网络的MEADS算法。为了降低训练样本时计算量，提高拟合精度，网络结构分为3部分：输入层、隐层和输出层；采用多输入单输出，每一个大气数据参数单独用一个神经网络来拟合。采用Levenberg-Marquardt(LM)方法作为神经网络的训练方法。

针对探测器进入火星大气层中出现的化学非平衡反应、大攻角和大分离状态等流动现象的压力计算，应用CFD方法研究具有非常明显的优势。采用自主研发CACFD大型计算流体力学数值模拟软件平台求解N-S方程，计算获得飞行器头部外形的压力分布作为神经网络样本训练的输入，神经网络采用4层结构(7-6-5-1)，输入层为7神经元，即7个压力数据点，中间隐层神经元数分别为6和5，输出层神经元数为1。对应的来流状态，如静压、马赫数、攻角和侧滑角作为样本的目标训练神经网络。在高性能并行机群上进行批量计算，通过数据提取和整理，建立来流状态与MEADS测压点对应的压力值数据库，作为神经网络的训练输入，训练神经网络，建立了高精度MEADS求解算法模型。

3.2 宽速域火星大气数据测量建模设计

火星探测器大气数据测量的飞行来流参数为总压、动压、静压、马赫数、攻角、侧滑角、风速和大气密度。总压、攻角和侧滑角等3个参数可以直接建模求解，不受马赫数无关性影响。而动压和静压的测量受马赫数无关性影响，在高马赫数段无法直接建模测量。因此测量设计方案为：首先建模求解出总压、攻角和侧滑角。由于IMU可以测量探测器的飞行速度，按照现有的火星大气模型，获得沿弹道各个高度的声速，因此两者结合可以预估出飞行马赫数。正好可以解决高马赫数条件下MEADS测量存在的技术瓶颈。应用MEADS求解出来总压、攻角和侧滑角后，根据正激波关系式和等熵关系式，分别求解静压和动压，参考式(6)和式(7)。

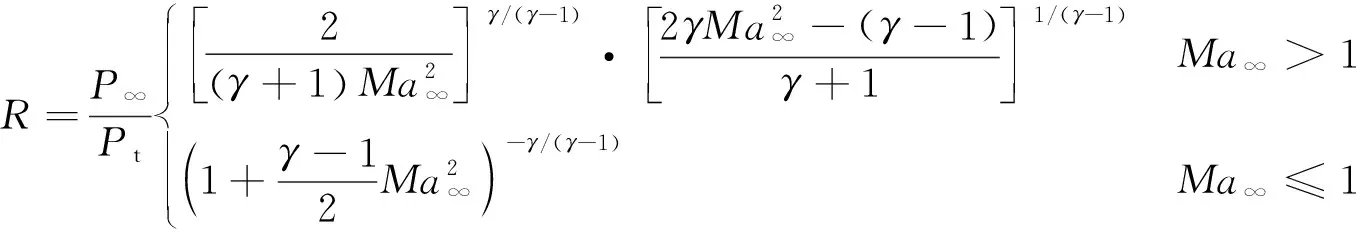
(6)

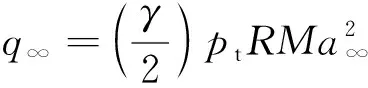
(7)

式中：为压比;为比热比;为来流静压;为总压;为来流马赫数。

图8为和变量随马赫数的变化。引入IMU测量马赫数计算动压和静压，图9所示为MEADS/IMU耦合测量方案。按照上述方案建模获得的马赫数、动压和静压未包含火星大气风速影响，但是由于马赫数高，所以风速影响较小。本文研究发现在≤12飞行弹道，马赫数的无关性影响降低，可以直接建模求解马赫数、动压和静压，测量结果则包含火星大气风速的影响。由于飞行弹道马赫数范围非常宽，因此样本点设计采用沿弹道分段阵列加密设计方法，确保每个马赫数段均获得合理的样本分布。通过多轮优化遴选合适的拓扑结构、传递函数、学习率和训练步数等，通过模型仿真测试厘清各参数影响关系，最后获取最优的建模参数。

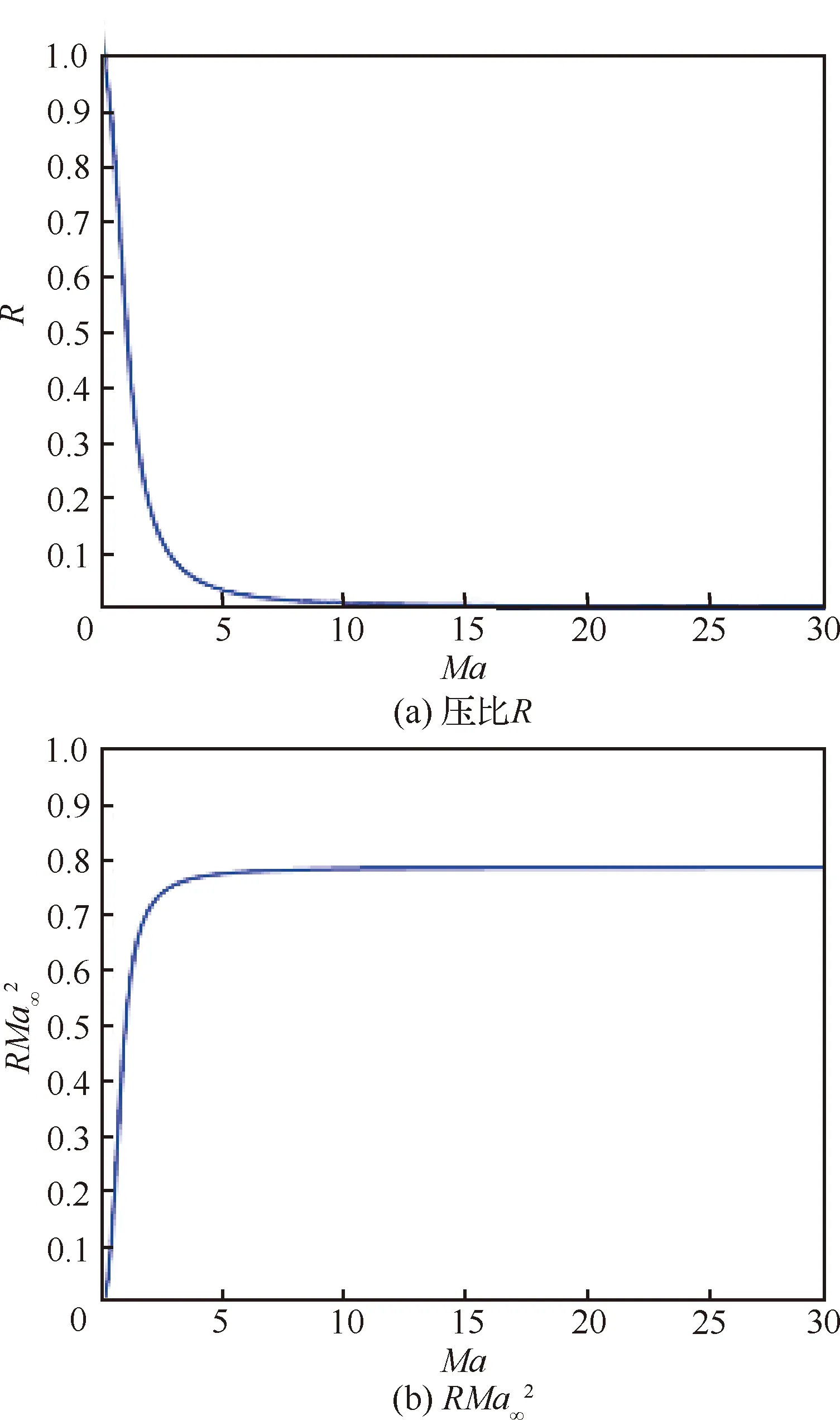
图8 R和RMa∞2随马赫数的变化Fig.8 R and RMa∞2 variation with Mach number

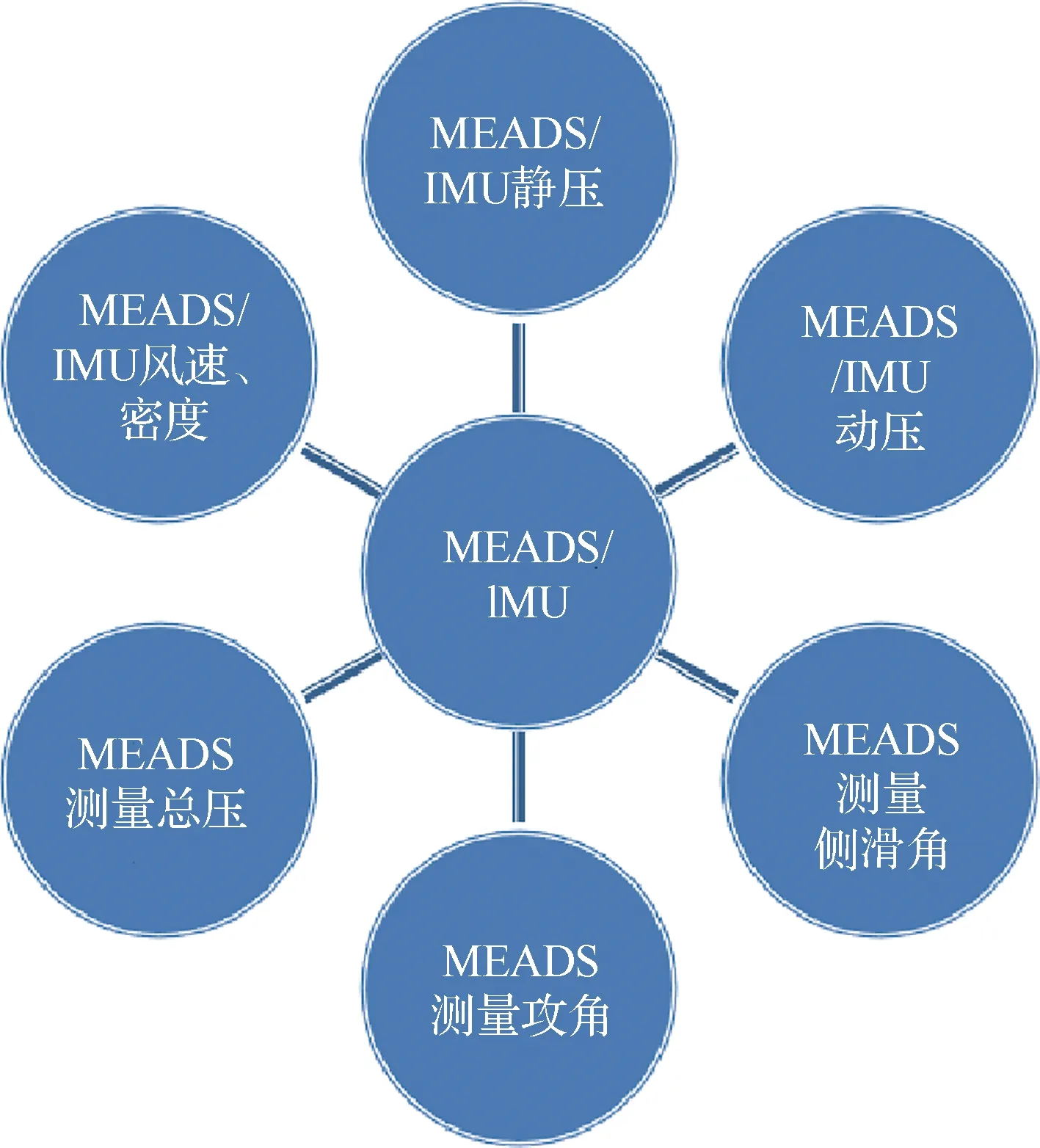
图9 MEADS/IMU耦合计量方案Fig.9 Coupling measurement scheme of MEADS/IMU

根据探测器结构约束要求,0°、90°、180°和270°的子午线均无法布置测压点，测压点只能在45°、135°、225°和315°子午线上布置，并且必须避开结构限制区域。因此测压点P4～P7只能在子午线上向外侧到离大底附近区域布点，寻找最优的布点方案。目前由于受到内部载荷和结构限制，只能安装7个测压点,如图10所示,为MEADS测压点布局。

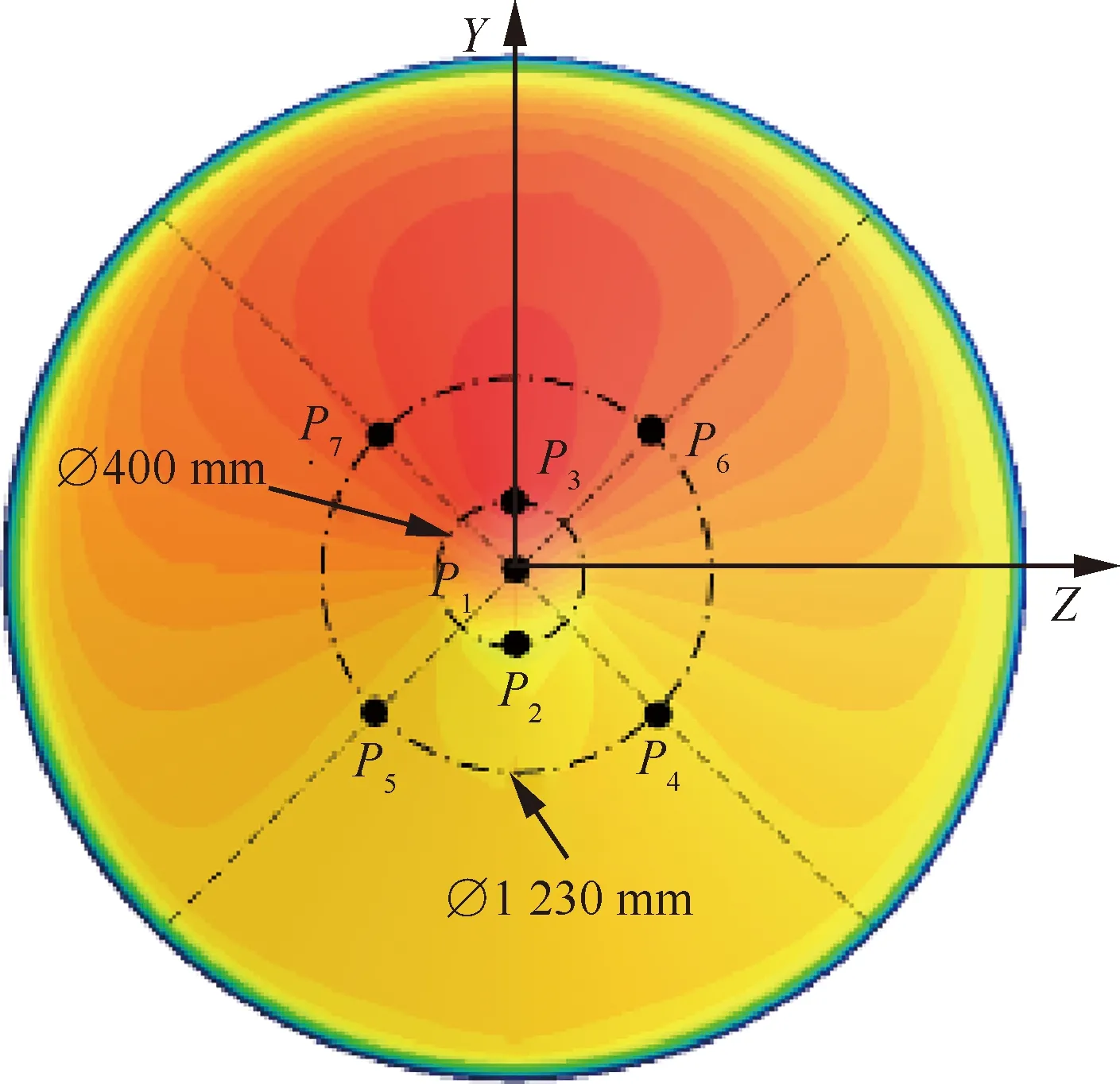
图10 MEADS测压点布局测量算法方案Fig.10 Configuration algorithm scheme of Mars probe points of MEADS

4 结果分析

在高超声速段(≥5)采用8组份(CO，CO，O，O，C，N，N，NO)化学非平衡模型计算火星探测器流场。在超声速段采用常规完全气体模型计算火星探测器飞行流场，完全气体模型的介质为CO。采用化学非平衡模型计算流场获得测压点数据，共计算195个状态，将正侧滑转换成负侧滑后共325个状态，采用完全气体模型计算流场获得测压点数据，共计算147个状态，将正侧滑转换成负侧滑后共245个状态。训练样本共计570个状态。仿真测试弹道点从标称弹道选取，从100 s开始(海拔约45 km)每隔5 s选取一个测点，共计37个点，马赫数范围从25.5～2.0，图11 所示为沿测试弹道MEADS测压点的CACFD计算结果。从图中可以得出最大压力值≤9.8 kPa，最小压力值≥1 kPa。假定测压单元总误差为测压点值(～)的3=1%，IMU测量马赫数误差为3=3%，以该误差作为测量误差仿真测试的设计输入。

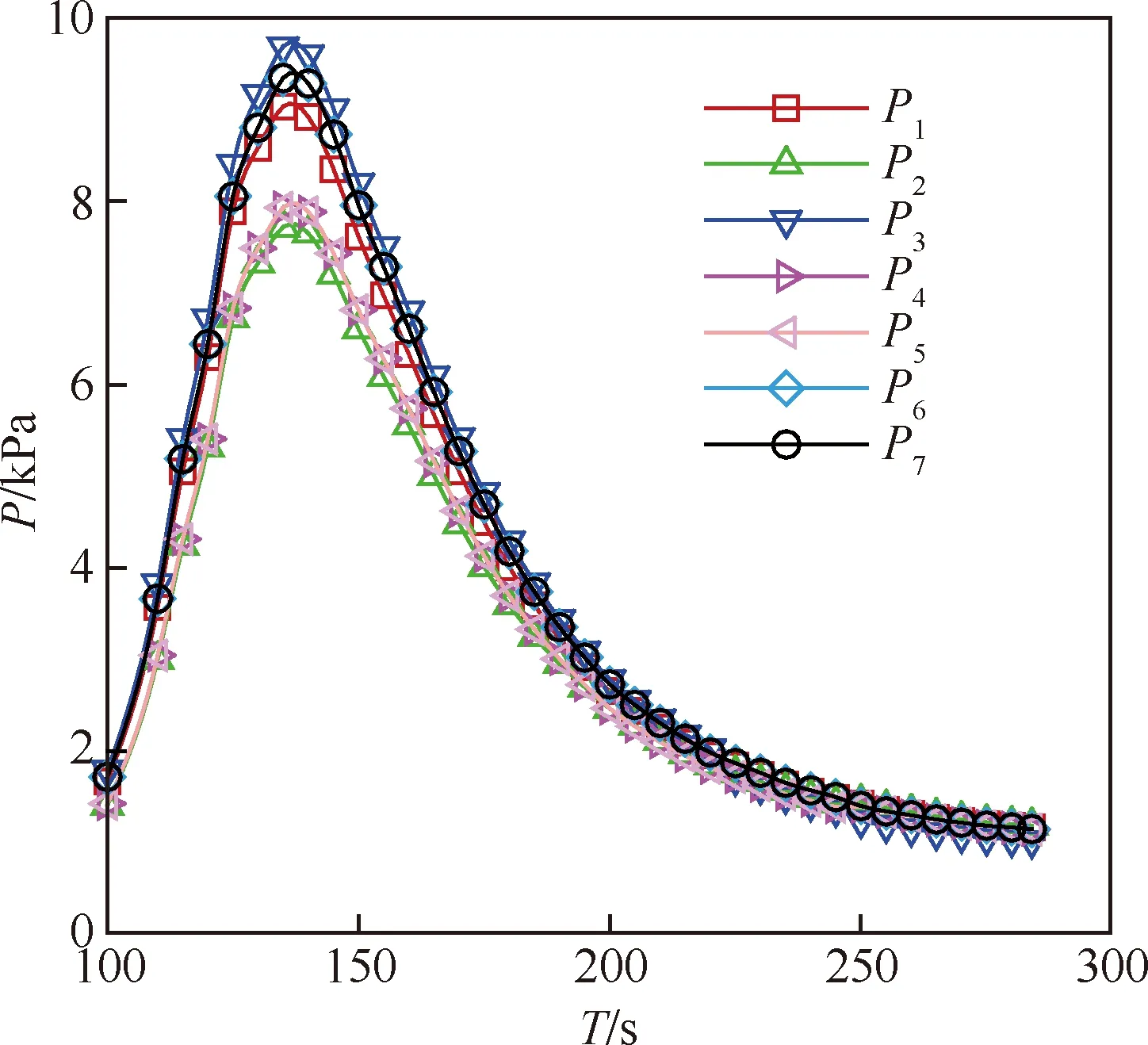
图11 MEADS测压点计算结果Fig.11 Computation results of MEAD configuration points pressure

4.1 MEADS/IMU耦合建模测量结果

总压、攻角和侧滑角模型的训练结果见图12，总压模型的训练误差≤0.014 kPa(14 Pa)，攻角模型和侧滑角模型的训练误差均≤0.5°。图13为MEADS模型的解算结果和测量误差。从图13(a)可以得出总压模型的解算误差≤20 Pa，测量误差≤2%。从图13(b)可以得出攻角模型的解算误差≤0.6°，测量误差≤1.6°。从图13(c)可以得出侧滑角模型的解算误差≤0.2°，测量误差≤1.5°。动压和静压的解算结果是利用IMU给出的马赫数和MEADS测量的总压，通过式(6)和式(7)换算获得。从图14(a)可以得出，动压的解算结果与标称弹道非常吻合，解算误差≤10 Pa，测量误差≤2%，与总压基本一致。从图14(b) 可以发现IMU测量马赫数的误差对解算动压不影响，这是由于在高超声速和超声速时，式(7)中的项接近常数，随马赫数的变化非常小，因此动压的解算结果不受IMU测量马赫数的影响。静压模型的解算结果和测量误差见图14(c)。从图14(c)中可以得出，静压的解算结果与标称弹道基本吻合，解算结果误差≤5 Pa；从图14(d)可以得出静压测量误差易受到IMU测量马赫数的影响，当IMU测量马赫数误差为0时，静压测量误差≤2%；当IMU测量马赫数误差为3%时，静压测量误差≤7%。

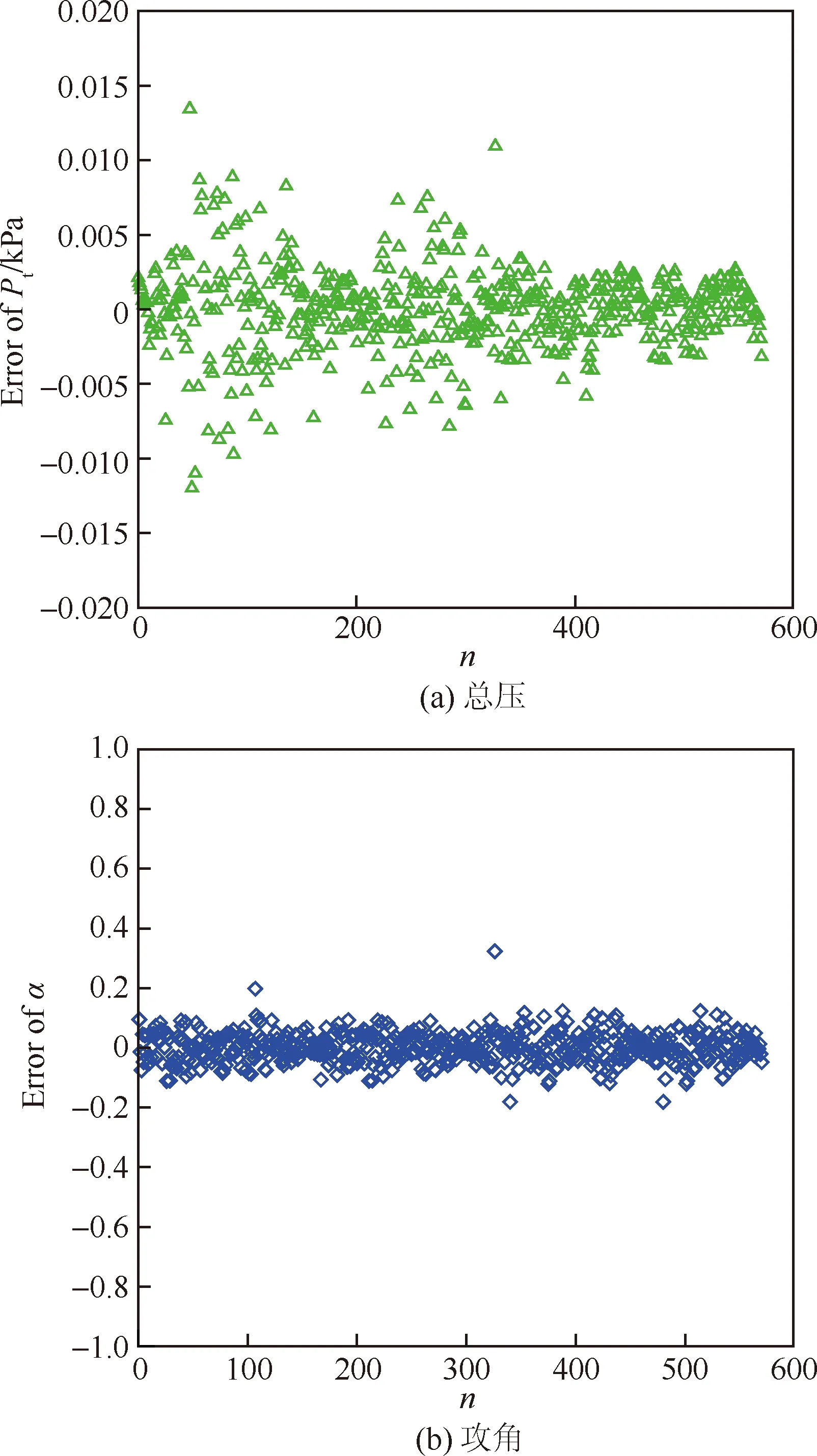
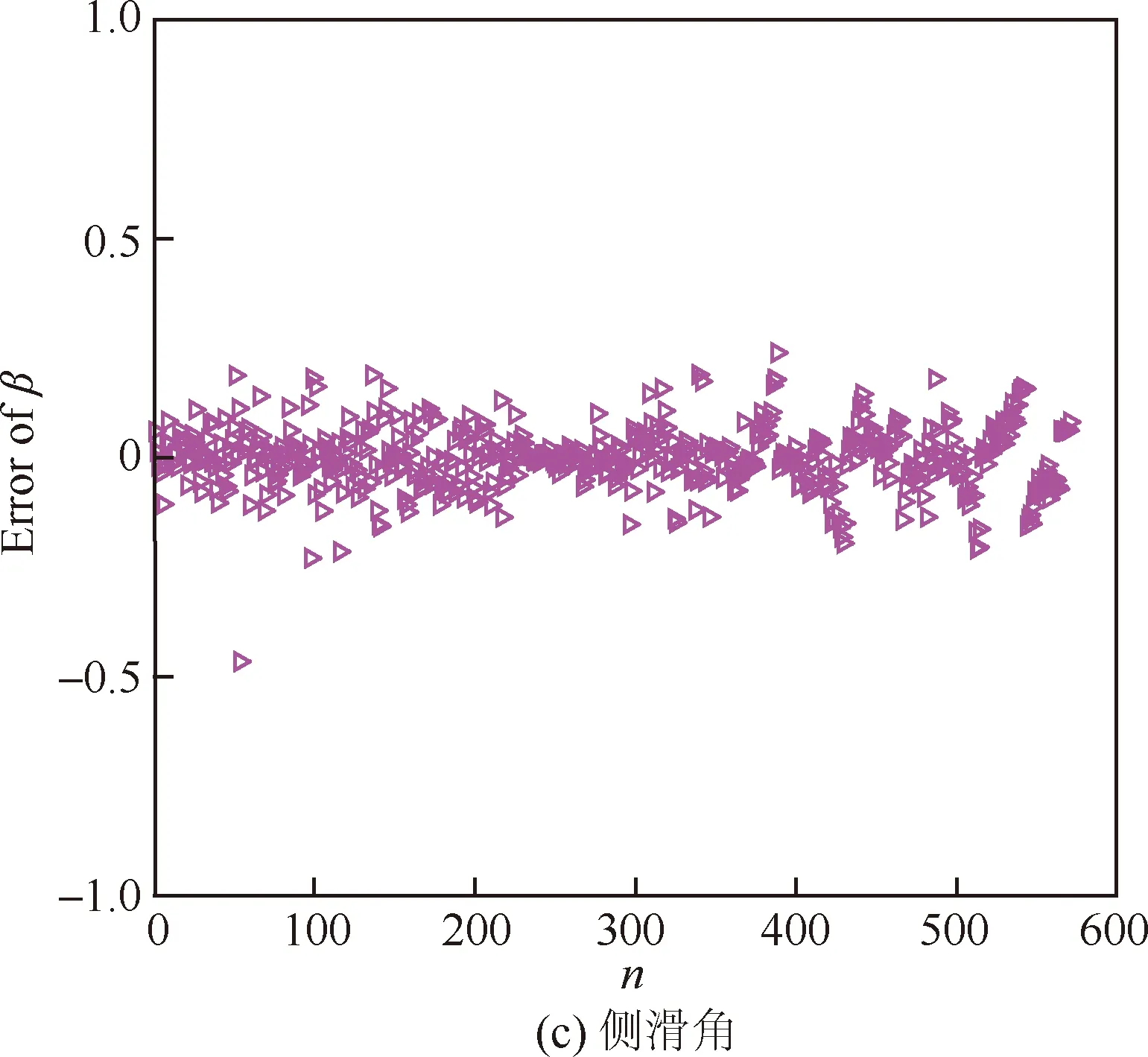
图12 MEADS模型训练结果Fig.12 Training results of MEADS models

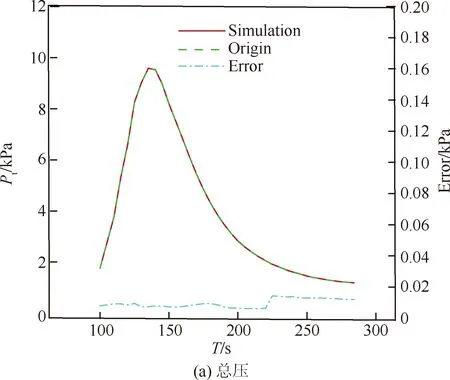
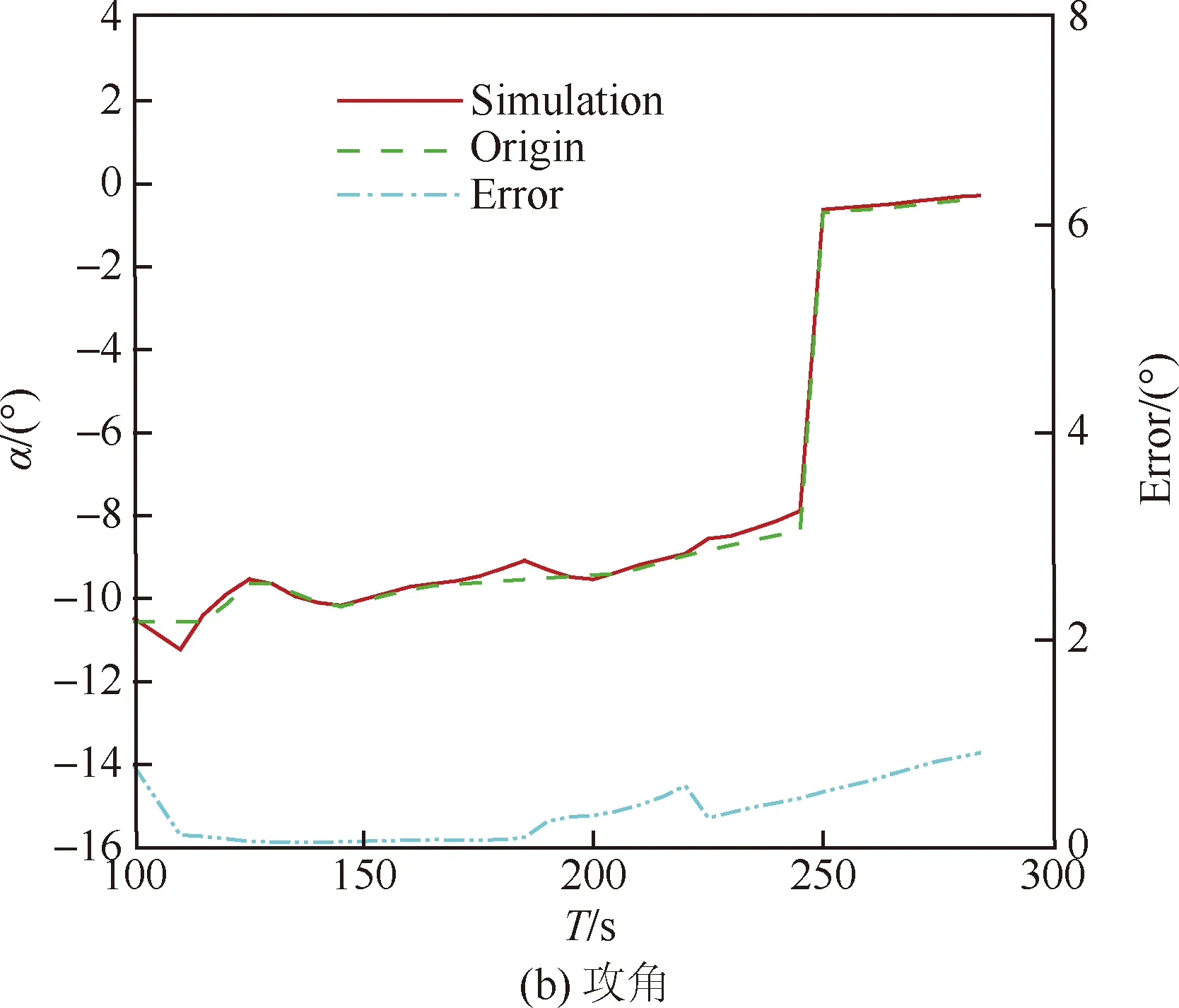
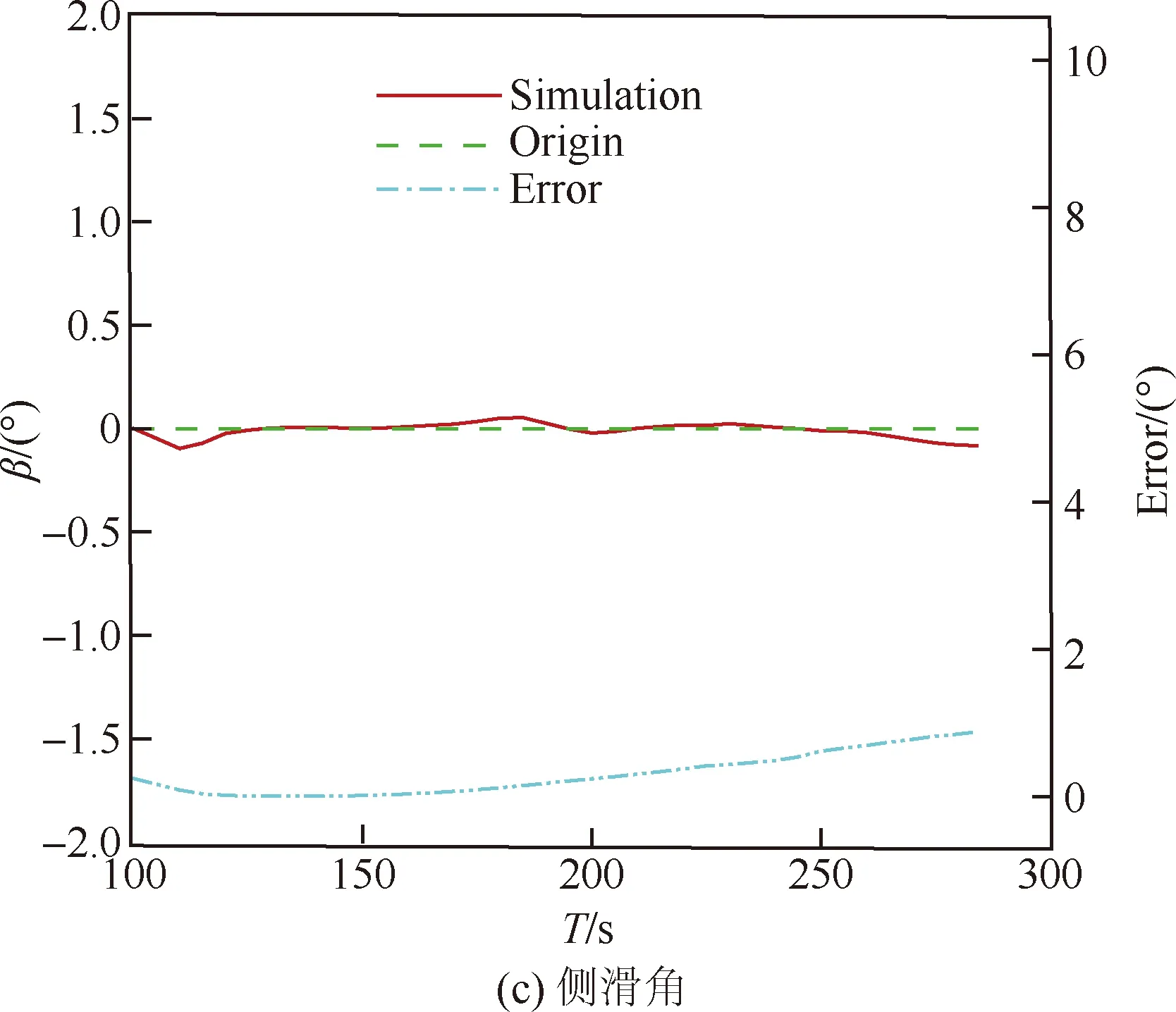
图13 MEADS模型解算和测量误差Fig.13 Results of solving and measurement errors of MEADS models

4.2 MEADS建模测量马赫数和静压结果

随着马赫数的降低马赫数无关性减弱，因此在低马赫数段可以利用MEADS模型直接解算获得马赫数和静压。从570个样本中取部分样本进行建模，分别取马赫数≤4的样本共245个、马赫数≤6的样本共345个、马赫数≤12的样本420个和马赫数≤20的样本共470个进行建模。从图15(a)中可以得出在>12时，马赫数测量误差急剧增大(≥5)，测量误差已经出现发散现象，模型的解算误差也达到1，因此在该段弹道马赫数MEADS建模失效，明显体现高超声速流动的马赫无关性特征。从图15(b)中可以得出在≤12时，马赫数的MEADS模型解算结果误差非常小，测量误差≤0.2。因此在≤12段可以直接建模，测量着陆探测器来流马赫数。图16所示为测压点总误差调整为3=7 Pa以后，马赫数的测量误差结果≤0.1；总误差调整为3=2%和3=3%以后,从图中可以得出测量误差分别为≤0.39和≤0.61，算法还未出现发散现象。图17(a)为静压模型的训练结果(≤12)，图17(b)～图17(d)为静压解算和测量误差结果。从图中可以得出静压解算误差≤10 Pa，测量误差分别为2.5%(3=1%/7 Pa)，5.5%(3=2%)，7.6%(3=3%)，基本上是按照线性增大的趋势。与图14(c)和图14(d)相比，直接建立静压MEADS模型解算获得的测量误差比MEADS/IMU耦合解算获得的静压测量误差明显偏小。

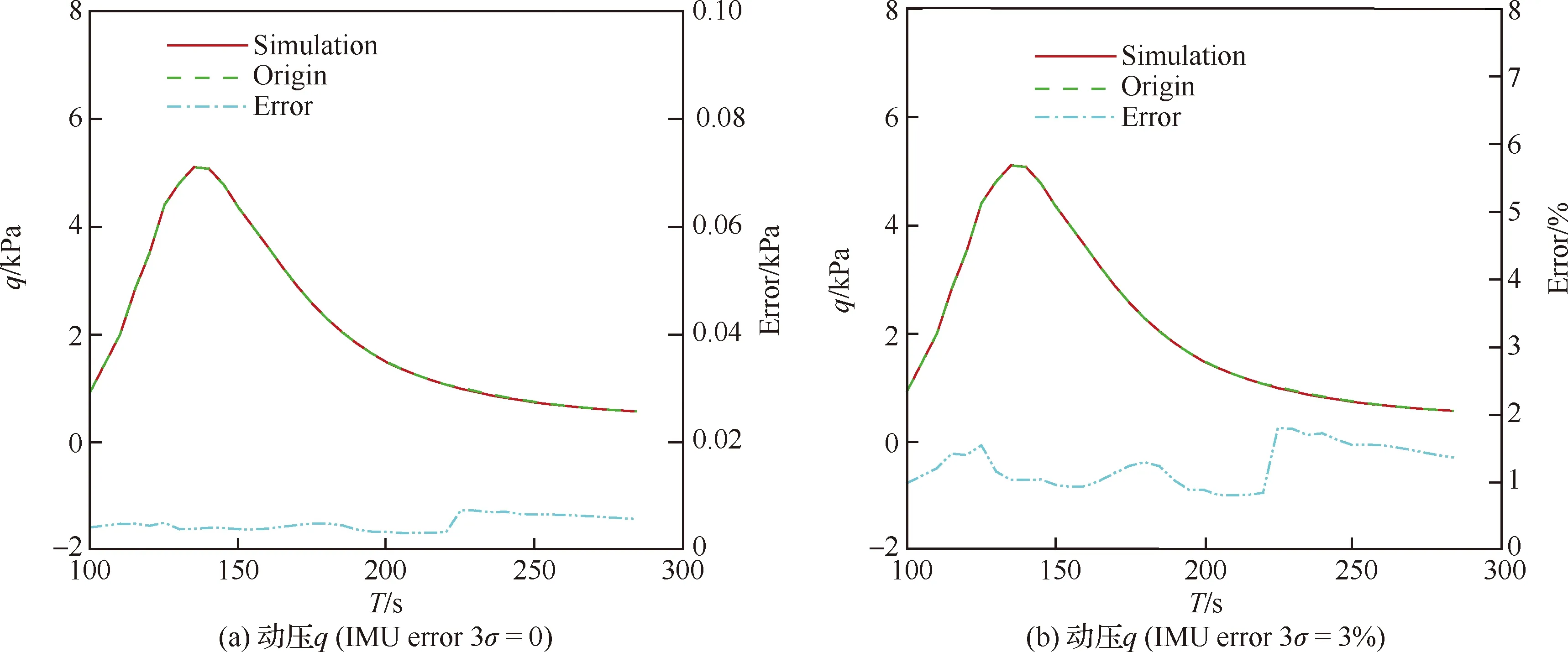
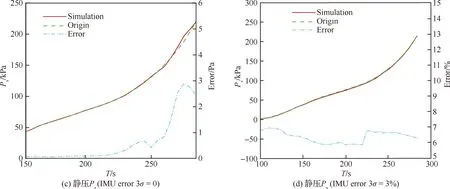
图14 MEADS/IMU耦合的解算结果和测量误差Fig.14 Coupled solving results and measurement errors of MEADS/IMU

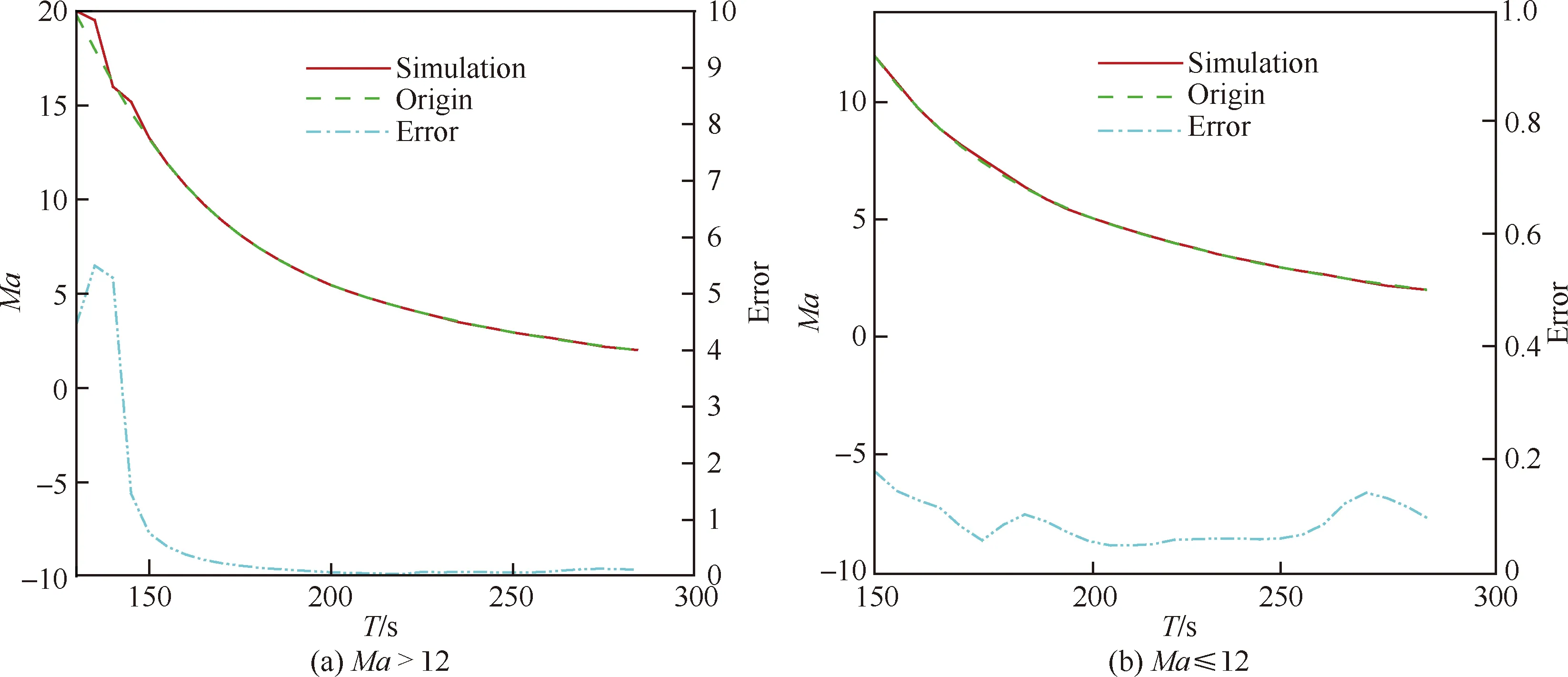
图15 马赫数解算结果和测量误差Fig.15 Solving results and measurement errors of Mach number

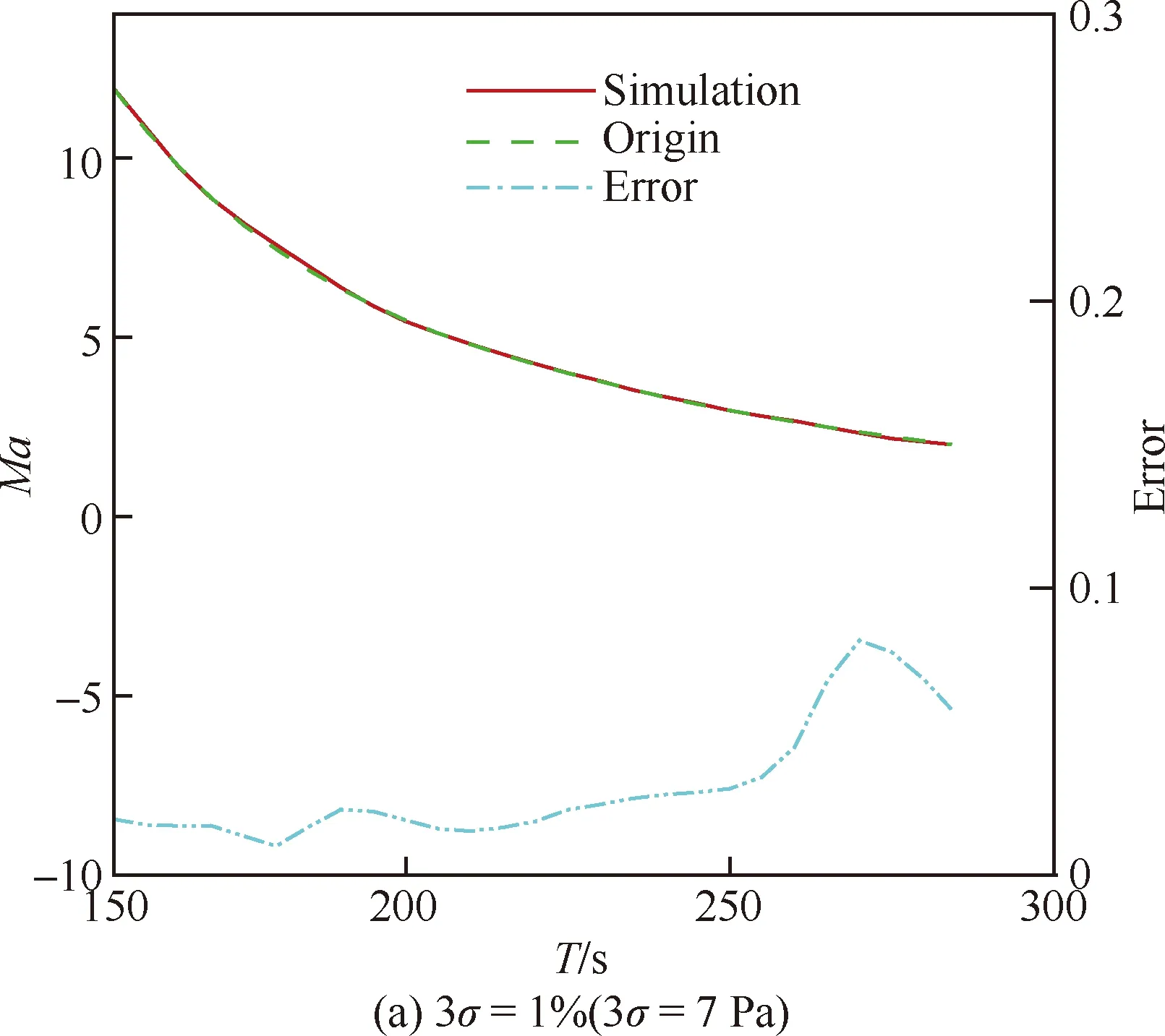
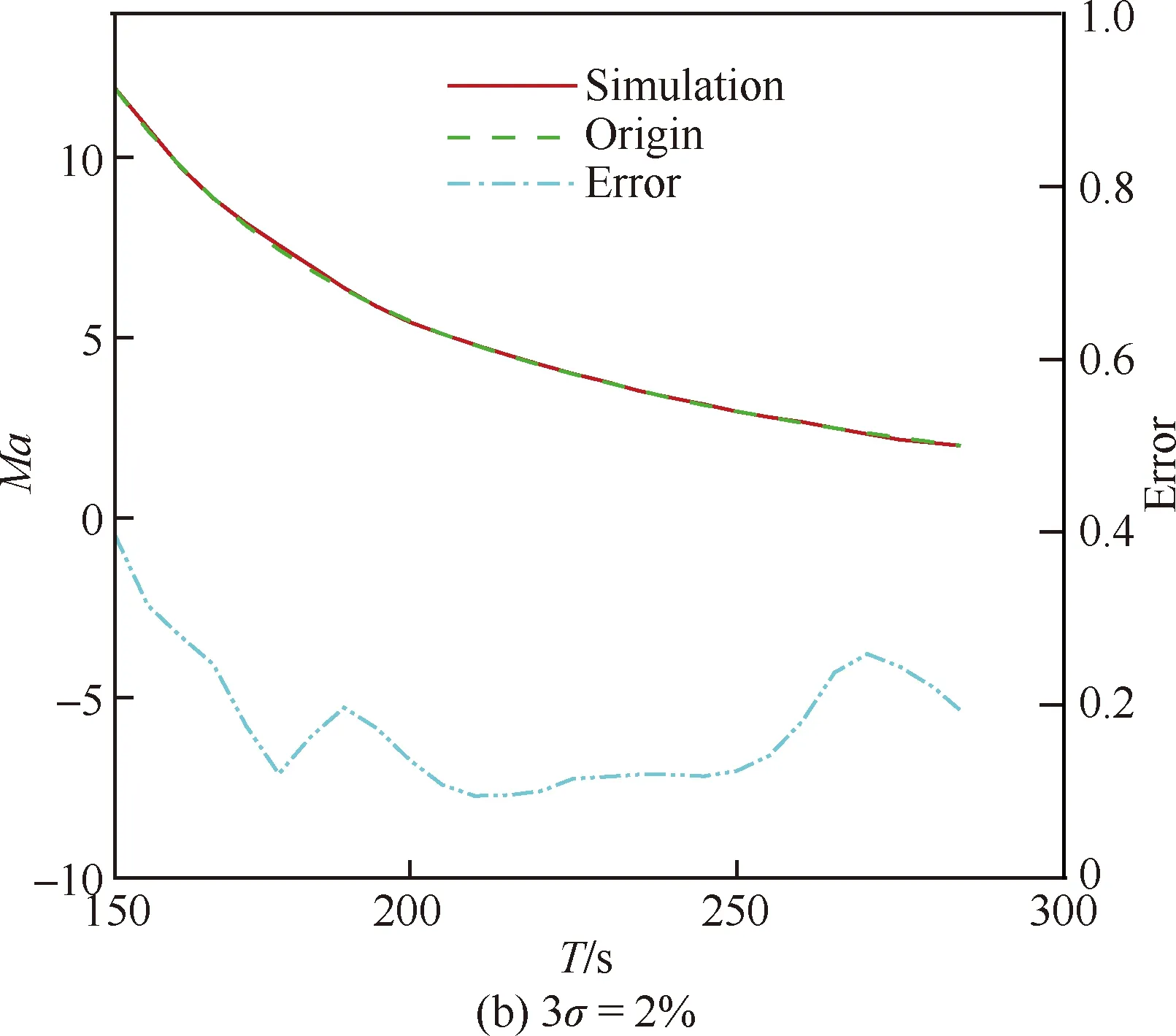
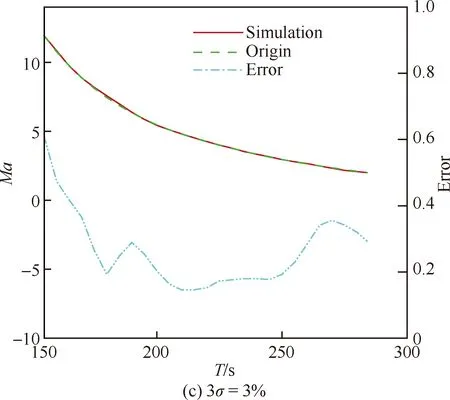
图16 马赫数解算结果和测量误差(Ma≤12)Fig.16 Solving results and measurement errors of Mach number (Ma≤12)

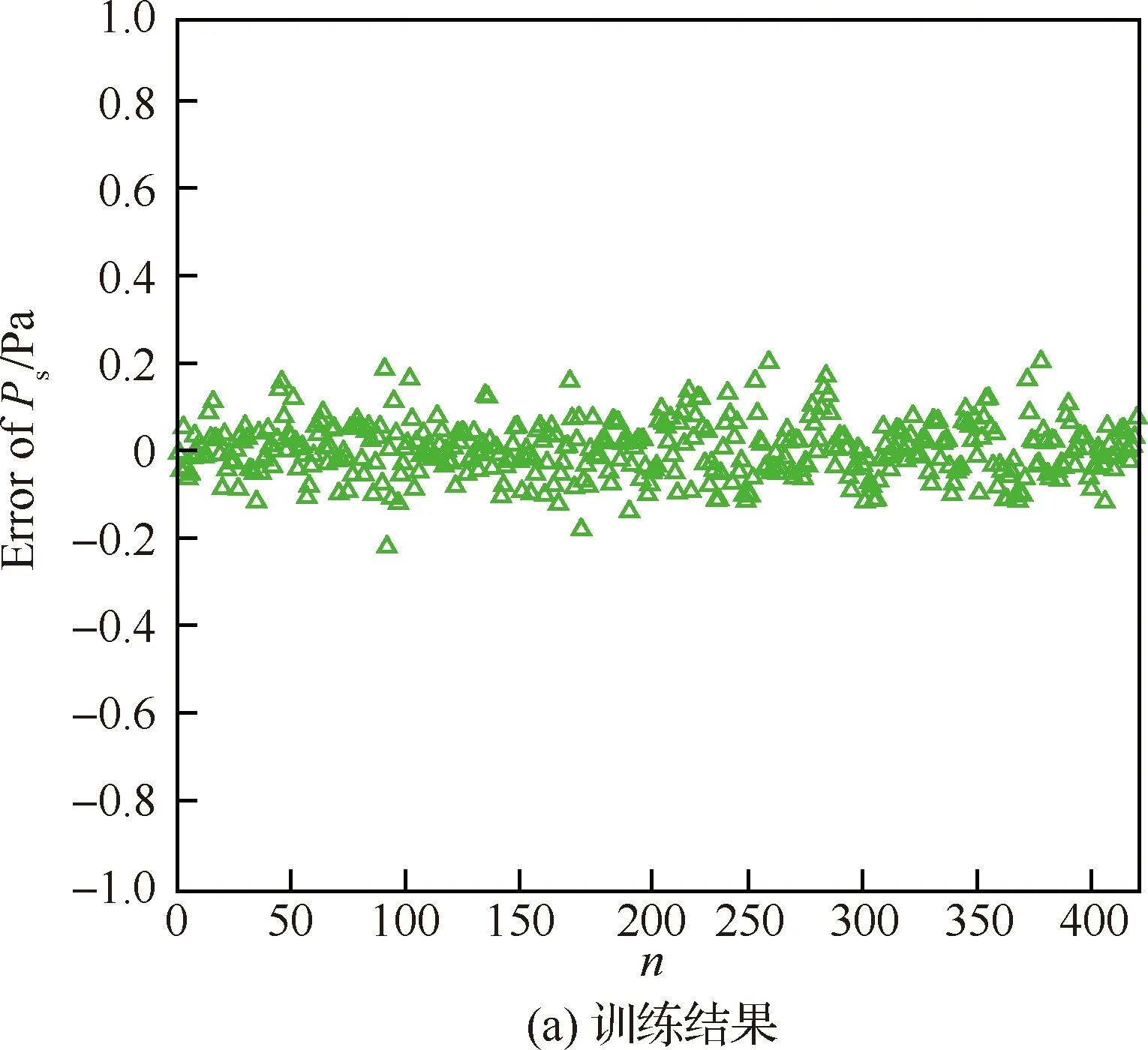
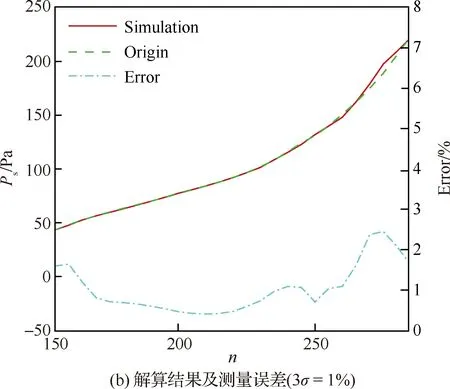
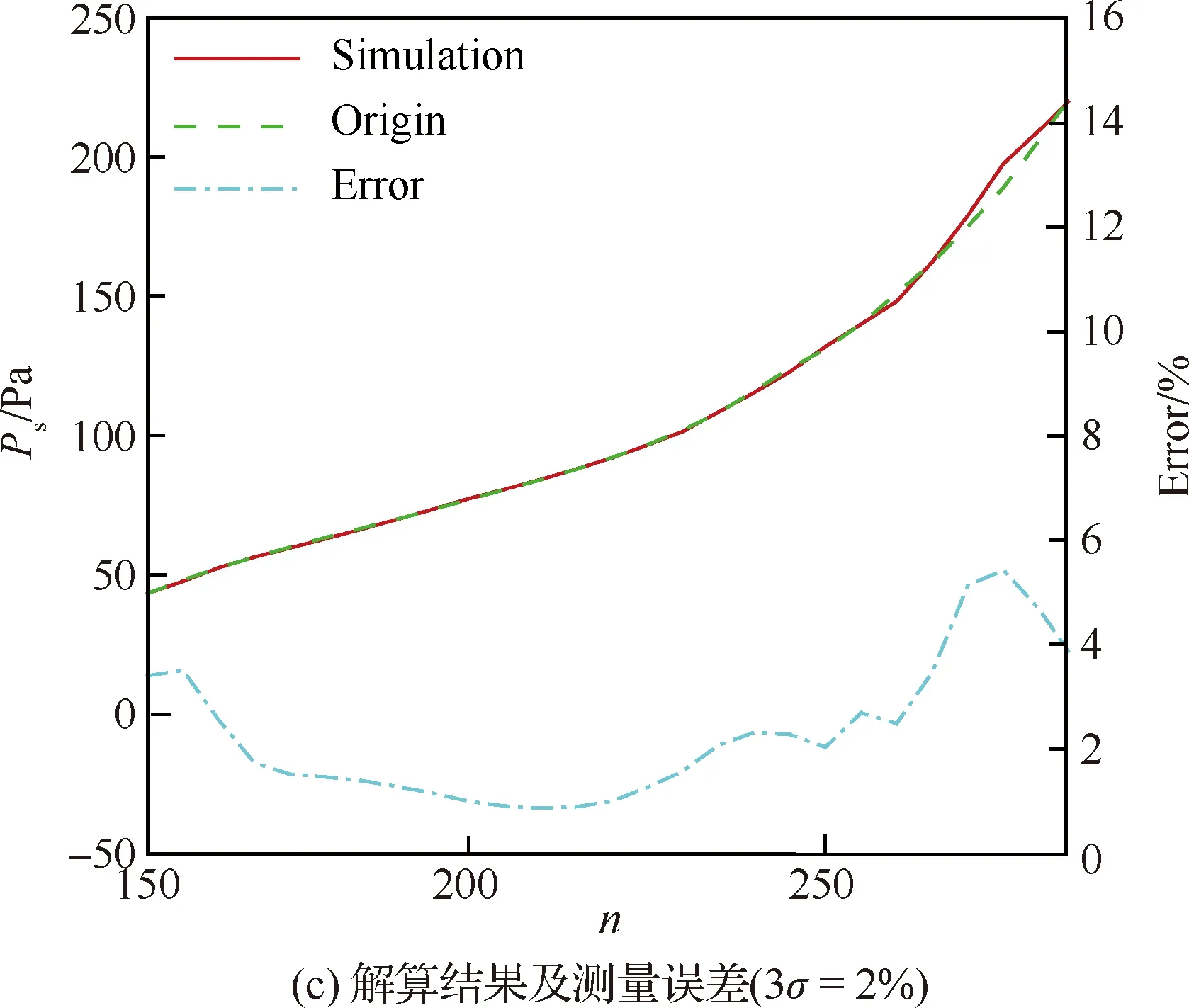
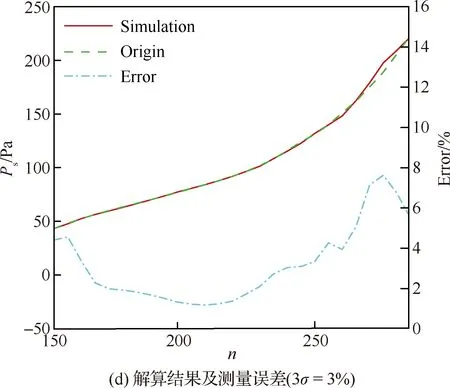
图17 静压模型训练结果和解算结果及测量误差Fig.17 Training and solving results and measurement errors of static pressure

4.3 测点布局优化结果

将～测压点向大底外侧延伸布置。建立MEADS模型分析测量误差的变化，如图18所示。图19为测压点布局B 的MEADS模型训练结果，图20为MEADS模型解算结果和测量误差。从图19(a)得出总压模型训练误差≤30 Pa，比测压点布局A的模型训练误差≤15 Pa略大。从图19(b)得出攻角模型训练误差≤0.1°，明显比测压点布局A的模型训练误差小。从图19(c)得出侧滑角模型训练误差≤0.7°，大部分样本训练误差≤0.2°，与测压点布局A基本接近。图20所示为测压点调整后建模的解算和测量结果。从图20(a)看出，总压解算误差与测压点布局A的接近，而测量误差≤2.2%，比测压点布局A的MEADS模型的测量误差(≤2%)略大。从图20(b)和图20(c)可以得出攻角和侧滑角的解算误差相对于测压点布局A不变，但是测量误差均减小，攻角测量误差≤1.1°，侧滑角测量误差≤1.0°，比测压点布局A的MEADS模型测量误差均降低0.5°。总体来看，测压点～往探测器大底外侧布置，与～的差压增大，有利于降低攻角和侧滑角的测量误差,而对于总压测量影响较小。

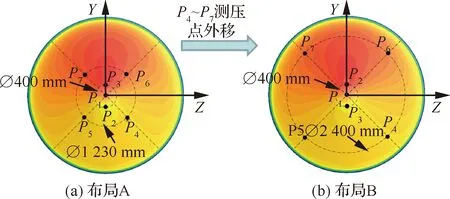
图18 测压点布局优化Fig.18 Configuration optimization for pressure points

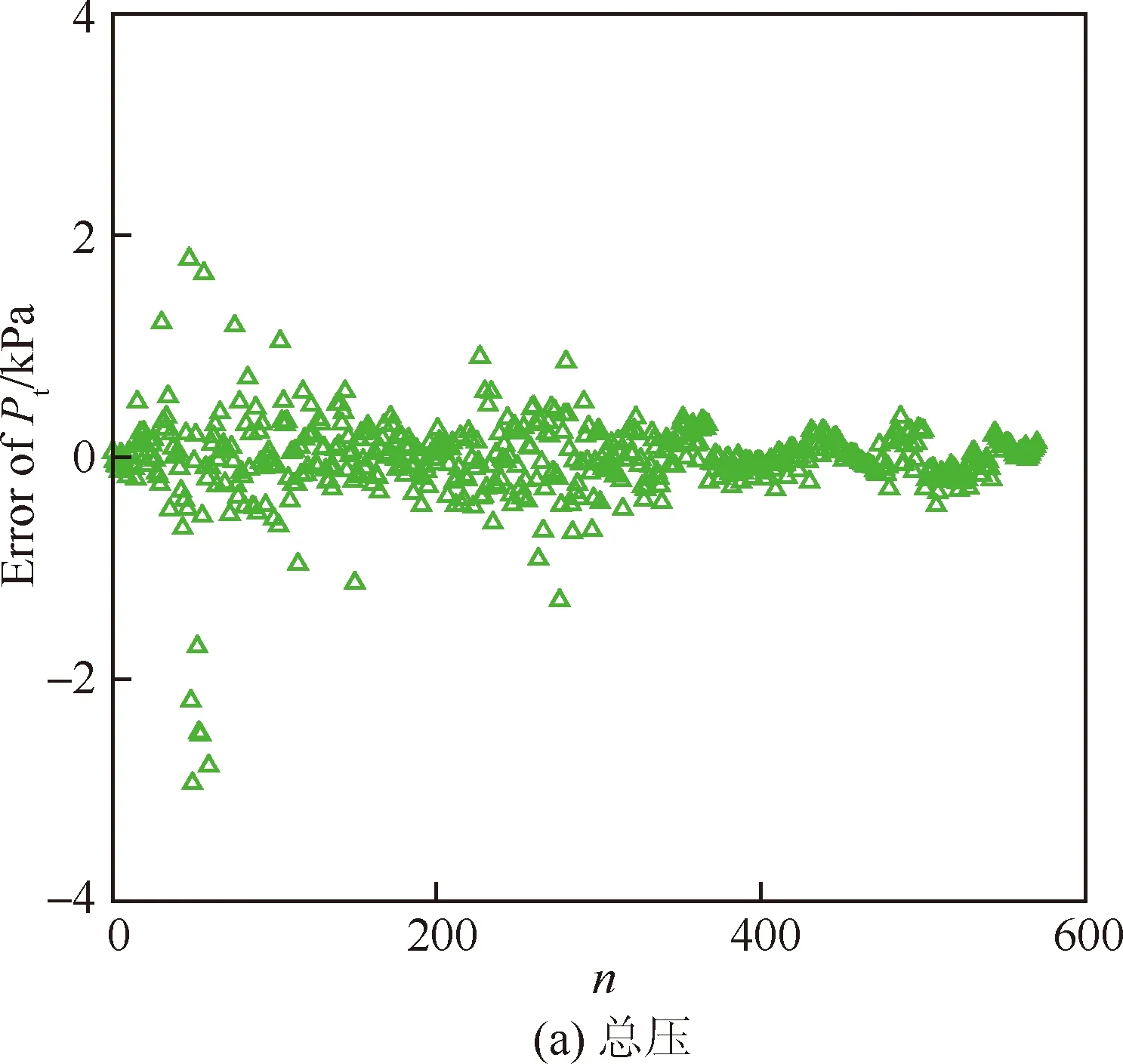
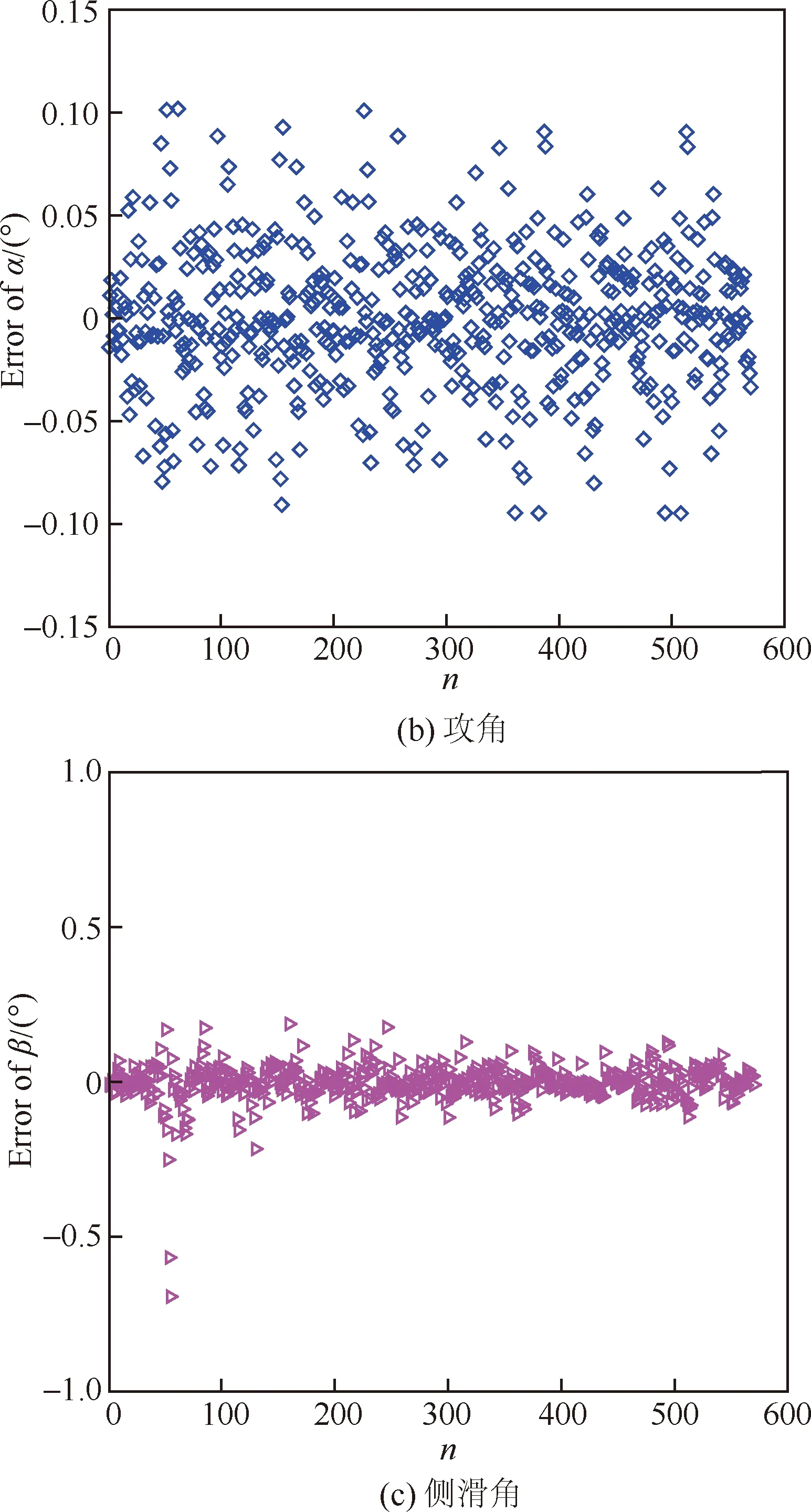
图19 测压布局优化后MEADS模型训练结果Fig.19 Training results of MEADS models after optimization measurement configuration

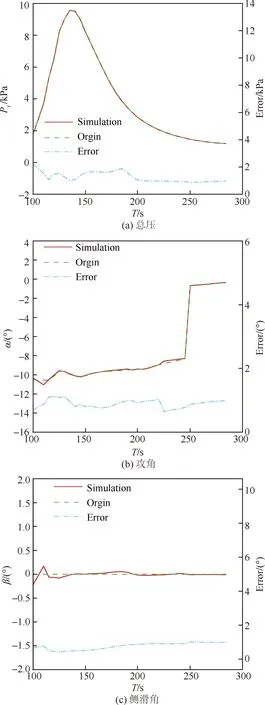
图20 测压布局优化后MEADS模型解算和测量误差结果Fig.20 Solving results and measurement errors of MEADS models after optimization measurement configuration

4.4 飞行试验结果

飞行试验测量结果如图21～图29所示。图21 为7个测压点飞行弹道测量结果。图22为总压和动压测量结果。图23和图24分别为动压和总压测量结果与标称弹道的对比。除了飞行高度出现一定偏差外，动压和总压测量结果与标称弹道变化趋势基本一致；动压最大值分别为5.135 kPa 和5.146 kPa，总压最大值分别为9.801 kPa和9.662 kPa，基本吻合。图25为马赫数测量结果对比。从图25中得出MEADS的马赫数测量结果与IMU测量结果基本吻合，在高超声速段最大偏差约为1，超声速段最大偏差约为0.3。

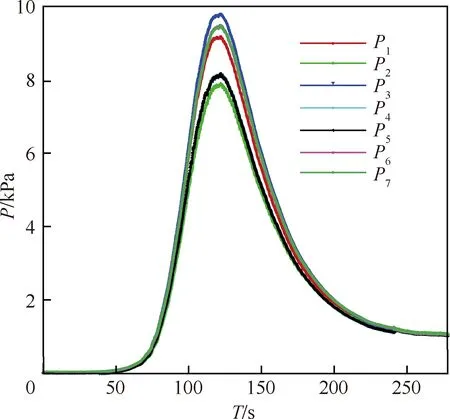
图21 测压结果Fig.21 Pressure measurement results

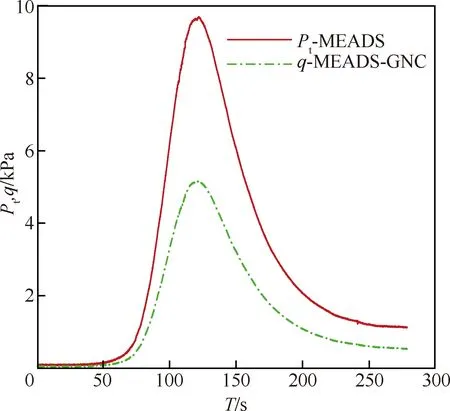
图22 动压和总压的测量结果Fig.22 Measurement results of dynamic pressure and total pressure

图26和图27所示为攻角和侧滑角测量结果对比。从图中可以得出由于弹道两端动压较低，因此测量结果出现严重振荡。取飞行弹道85～200 s段攻角进行对比，可以得出MEADS的攻角和侧滑角测量结果与IMU的测量结果基本一致，最大偏差约为2°。

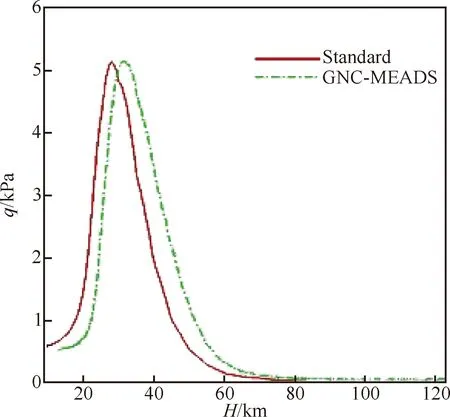
图23 动压测量结果对比Fig.23 Comparison of dynamic pressure

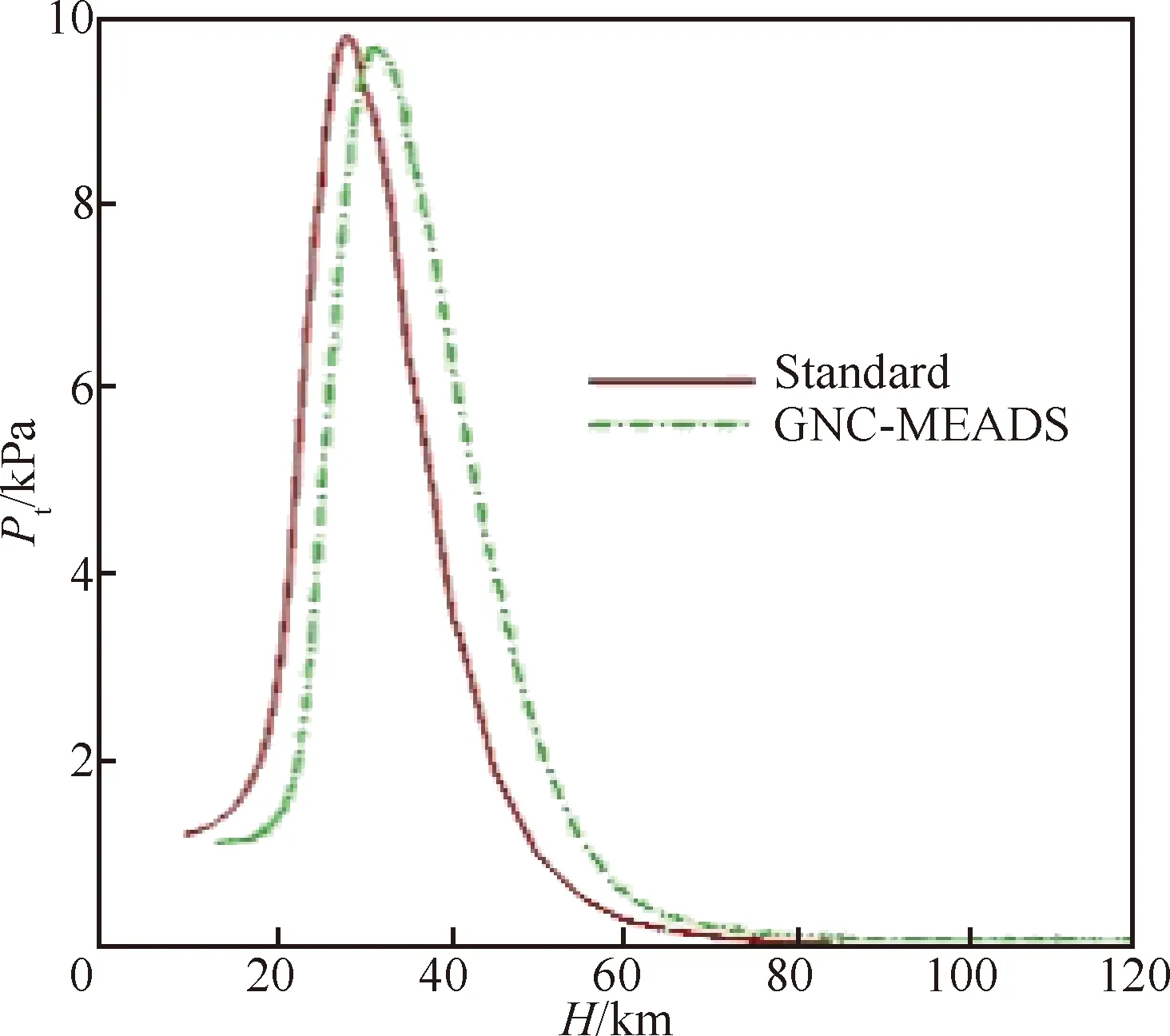
图24 总压测量结果对比Fig.24 Comparison of total pressure

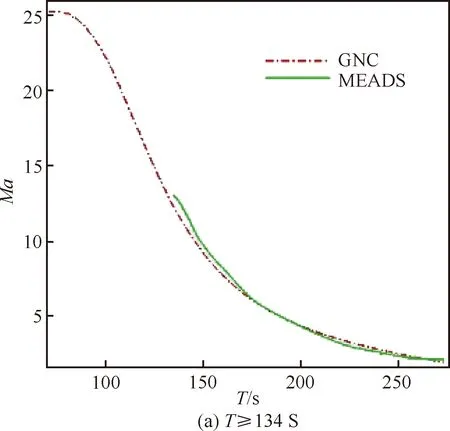
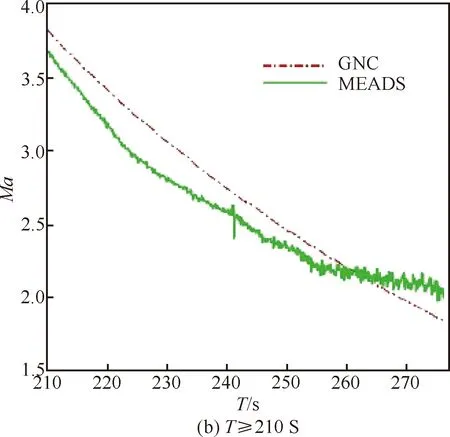
图25 马赫数测量结果对比Fig.25 Comparison of Mach numbers

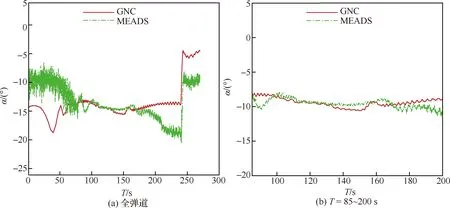
图26 攻角测量结果对比Fig.26 Comparison of angles of attack

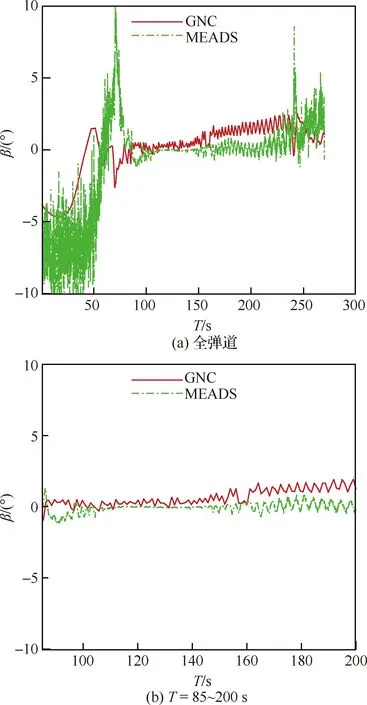
图27 侧滑角测量结果对比Fig.27 Comparison of angles of sideslip

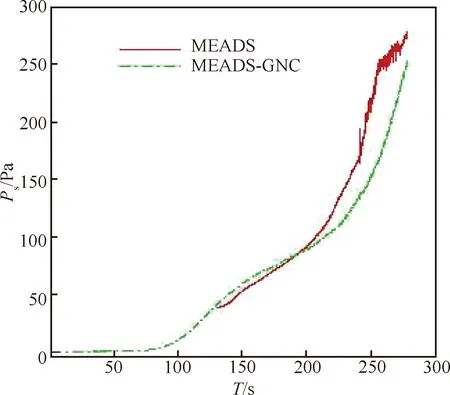
图28 静压测量结果Fig.28 Static pressure

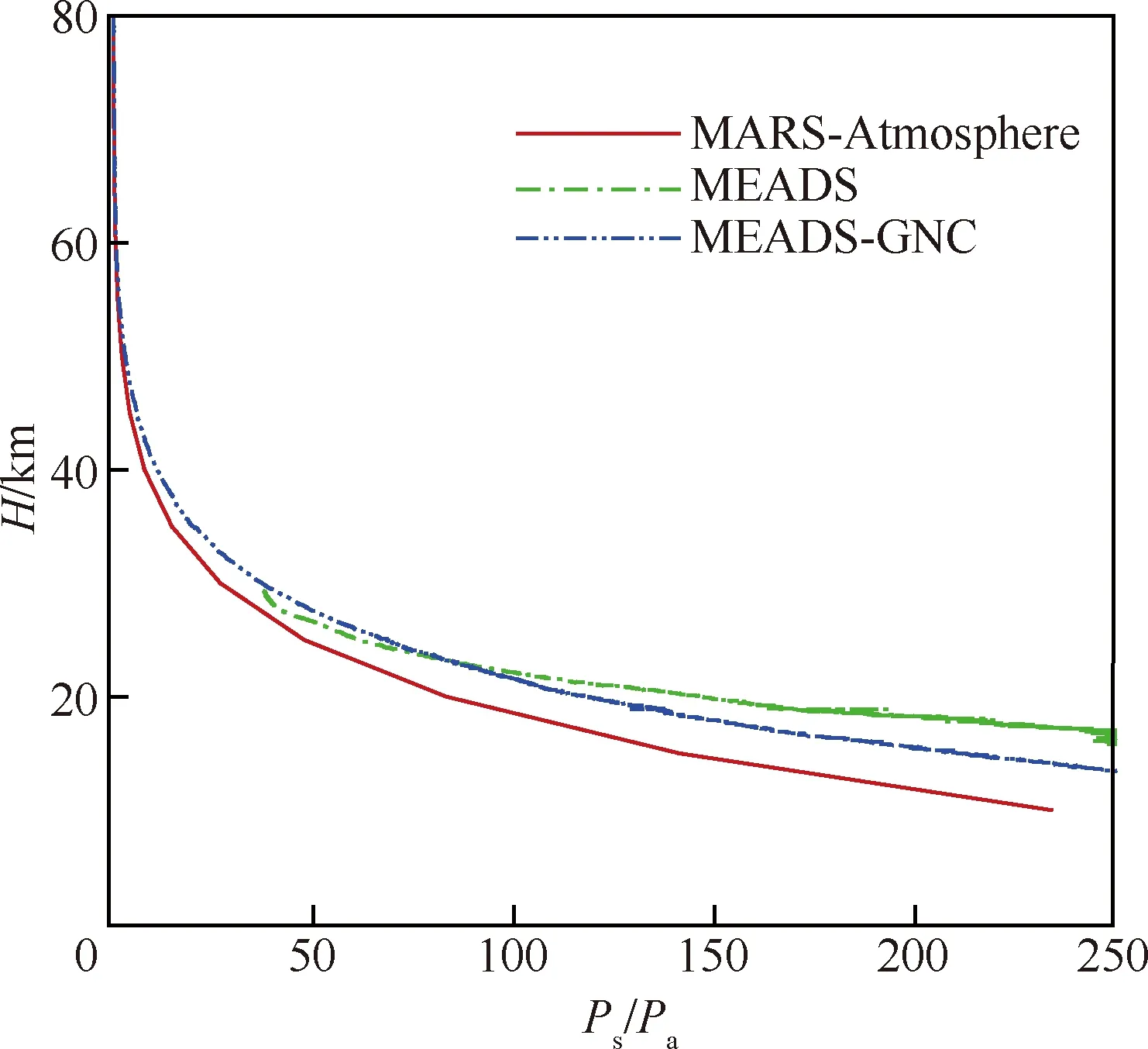
图29 静压测量结果对比Fig.29 Comparison of static measurement results pressure

图28和图29所示为静压测量结果对比。从图28得出，在130～210 s段静压吻合较好，在210 s以后两种方法的静压测量结果偏差最大达到70 Pa。图29所示为静压测量结果与火星大气模型(欧空局提供)对比，从图中可以得出MEADS测量结果与欧空局提供的火星大气模型在偏差较大，特别是在20 km高度以下，静压偏差达到120 Pa，由于篇幅限制,在此暂不做分析。