极限思想在教学中的渐进理解

河北正定师范高等专科学校 杨晓然 贾小玲

在数学 的发展 过程 中，极限 的概 念有着举足轻重的地位。这决定了在数学教学中，极限的教 学必须 要深 入浅出 。极 限是高中数学与大学数学的衔接部分。透彻理解极限，对于 大学微 积分的学习 也起到 了至关重要的作 用。 因此，极 限的 学习与 教学显得尤为重要。

一、极限思想发展与演变

极限的思想早在古代就已萌生。古希腊数学家阿基米 德“穷 解法”求抛 物 弓 形的面 积，构造 了一系列 三角形 ，使 它 们 的面积和不断接近抛物弓形的面积。中国古代数学家刘徽 （公元 3 世纪）“割圆术”利用圆内接正n边形边数n无限增大，则正多边形面积无限接近于圆的面积。这些都是极限最初的形式。

十 九 世纪法 国 数 学家柯 西 从 定 性 的角度比较完 整地说 明 了 极限概 念 及 其理论。之后，德国数学家维尔斯特拉斯给出了极限的定量定义。

了解极限思想的发展史，可以使学生在理解极限 时更有 兴 趣 ，也更 有 数 学根据。只有这样才能使极限更好地融入学生的心理。

二、极限 概念和 高等 数学中 微积 分学的关系

数学是 一门基 础学 科 ，它的 基础性 与应用广泛性是任何学科所无法比拟的。一切的自然科学 ，各个 经济生 活领 域都有 数学留下的足迹 ，因此 可以说 数学 是学科 界的“学科先 驱”。运用 数学 思想，数 学方 法思考和解决问 题，不仅 可以 培养人 们科 学的世界观，而且 可以使 人们 在解决 任何 实际问题时具备严谨的科学态度。如果把整个高等数学 看作 一个人 体，那 么极限 是高等数学中微积分的主动脉。导数与微分可以看到定义 的新 运算，这 种运算 类似 小学所 学 的 加 减 法 和 乘 除 法 中 互 为 逆 运 算 一样。导数和 微分 也应该 有逆 运算，可 以说“ 不 定 积 分 ”与“ 定 积 分 ”是 导 数 的 两 种 不同的逆运算。导 数、微 分、不定 积分 、定积分这四个概 念虽然 各不 相同，但 它们 存在着极其密切 的 关系 ，即它们 的概 念中都 贯穿了极限概念。

三、极限思想的教学演变

在新课程改革 （人教 A 版 2007 与人教 A 版 2017 数学课本） 中都将微积分放在了高中数学课程的重要位置上，并且在内容上都体现出了极限思想这一数学思想，说明了极限思想在高中数学教学中的重要性。本文从极限的概念出发，阐述极限教学中学生的学与教师的教的难点与重点并结合高中数学与大学数学的理解差异，比较两者教学差异，让学生能更好地理解极限的思想。

四、学生学习现状分析

在 2007 年 新课 程改革 中， 之 前 很 多传 统 上 在 高 校 数 学 课 堂 中 讲 解 的 内 容 也成为了高中 数学的 重点 。比如 ：极限 ，导数 ，定 积 分 等 。 实 际 上 ，由 于 高 考 指 挥 棒中，要求学生必须会应用这些知识。但是，是否能够真正 理解 ，这有待 考究 ？由于 高中应试教育背 景下 ，学生对 于应 用导数 来解 决 单 调 性 ，极 值 ，最 值 ，零 点 ，不 等 式 等问题比较熟练 。但是 学生 对于极 限，导 数等的概念的理解却深浅不一。

实际上，这 样的教 学会 使学生 产生 很多误区。学生对于初等数学与高等数学在思维方法，研究 内容的 侧重点 的差 异认识不够。尽管学生们对于极限部分有一定的基 础 ， 但 是 这 种 基 础 能 起 到 什 么 样 的 作用？这些都是 有待对 学生 的了解 和分 析 。倘若学生思维认 识不 到位 ，问 题可 能就会想不明白。如果 没有 清晰和 明确 的认知 ，就不会去直观地 理解 ，更别说 用数学 精确语言去描述极限概念了。

种种问 题与 困惑交 织在 一起，使 得学生对极限的学习比较迷茫。感觉自己好像学过，但是 好像 又 没有 学过 。 学习 中表现出来的是：一方 面，感 觉已经 懂了 ，不屑于听 ；另 一 方 面 ，接 触 高 等 数 学 中 极 限 定 义之后发现 自己又 一无 所知，颠 覆了 之 前对于极限的所 有认 识，感觉 像天 书一样 难以理解。在高 等数 学的教 学实 践中，往 往会发现学生有 上述 两种表 现。 因此，需 要引导学生端正 学习态度，走 出认识 和学 习误区就显得尤其重要了。

五、揭示本质属性，加深理解

对高等数学中微积分的极限概念的理解，从数列极限，函数极限（x→+ ∞,x→x0）的顺序进行教学，并要 对三种 极限 在概念方面进行差异的比较。

1 .数列极限。

（1）直观描述——定性定义。

如果数列{an}的项数n无限增大 时，其一般项{an}无限接近于某个确定的常数a，则称a为数列{an}的极限，或称数列{an}收敛于a，记作

数列{an}的极限为a的几何解释：

数列 {an} 中的项对应数轴上无数个点，点an与a接近的程度可以用它们之间的距离 |an-a|来衡量an无限接近于a，就意味着距离 |an-a|可以任意小.

（2）精确定义——定量定义。

若对任给的正数 ε（不论它多么小），总存在正整数N，使得当n＞N时有 |an-a|＜ε，

则称数列{an}收敛于a，记作

ε-N定义：N+，当n＞N时，有 |an-a|＜ε.

关于 ε-N定义，从以下理解：

①ε 的任意性。尽管 ε 有其任意性，但一经给出，就被暂时确定下来了，以便依靠它来求出N。又 ε 是任意小的正数，因此定义中 ε 的可以用等来代替。

②N的相应性。一般说，定义中的正整数N是一个与 ε 密切相关的项数，与N相对应的项是an。因此，常把N写作N（ε），来强调N是依赖于 ε 的。但是，这种依赖关系，也不意味着N是由 ε 所唯一决定的。这里重要的是N的存在性，而不在于它的值的大小。

从 几 何 意 义 上 看 ，“ 当n＞N时 ，有|an-a|＜ε.”表示点an与a之间的距离可以为任意小的正数 ε，它可以是 0.1 、0.01 、0.001 或更小。但不管多么小，数列{an}与a的距离 |an-a|，当n→∞ 时，总比 ε 还小，因而an与a可以任意接近。也就是说，在U（a；ε）之外，数列{an}中的项至多只有N个（有限个）。

通过直观定义 与精 确定义 ，可以 使得学 生 们 对 于 数 列 极 限 概 念 的 理 解 更 加 深刻。初等数学研究 的是 固定的 ，静态 下量与量之间的数量关 系。 然而，高 等数学 研究 的 是 量 与 量 在 运 动 变 化 过 程 中 的 数 量关系，这是初等 数学 与高等 数学 的根本 差异。因此，学生们由高中到大学的过渡，需要一个过程与时间。如果学生们有清楚与明确地认识到量与量之间的“运动”。在以后的高等数学 的学 习中，可 能相 对会容 易些。这就要求学生们应该从思维认识上要突破从有限过 渡到 无限，学 会并 习惯使 用数学语言描述 问题，使 得学 生的 思 维变 得更加严密。

基 于 以 上 学 生 们 可 能 在 初 入 大 学 时存在的问题，在教学中有哪些应对措施呢？一方面通过有 趣的 例子提 高学 生 认识 ，另一方面还是要帮助学生理清极限概念出现的内在逻辑过程，把握极限概念本质，引导学生能用以上的精确定义来描述极限。

找N可能出现两种情况：

①如果n＞N（ε），则即为所求。

②如果 |xn-a|＜ε 较繁琐时，可适当放大。如 何放大 ？可 以 放 大 为 如 下 形 式 ：|xn-a|＜g（n）。只要有，放大就是适当的！

由此可见，极限 的证 明步骤 几乎是 模板化的格式。以下就是证明的格式模板：

证：对∀ε＞0，要使 |xn-a|＜ε.

……这里是解 |xn-a|＜ε 的过程，得结果n＞ 某个数 （关于 ε 的表达式）；或当|xn-a|＜ε 比较繁琐不易解得，则在这里将|xn-a|作适当的放大，使 |xn-a|＜g（n），然后从g（n）＜ε 中解得n＞ 某个数。

取N= 某个数 （关于 ε 的表达式）或N= max{[某个数（关于 ε 的表达式）]，N0}，

则当n＞N时，有 |xn-a|＜ε 成立，

归纳出数列极 限的 一般证 明方 法，这样学生可能未必能够理解。但是，学生可以先模仿，在做题过程中可以边做边理解。最起码学生能够去做，可以有法可循。这样可以慢慢培养学生的兴趣。先做，再慢慢理解。数学也是一个理解和消化的过程。这样从定性理解，到定量计算。全方位的去理解，可以使得学生能够更好地接受。

“ 好 的 开 始 ，是 成 功 的 一 半 ”，数 列 极限 的 充 分 理 解 可 以 帮 助 学 生 更 好 地 理 解函数极限。

2.函数的极限。

（1）当x→+ ∞ 时，函数f（x）的极限。

①直观描述—定性定义。

当x→+ ∞ 时，函数f（x）的极限：

此种情况与数列类似，不同之处在于n→+ ∞ 是整序变量（n只取 1、2、3、……）等离散的正整数点变到 + ∞。而x→+ ∞时，函数f（x）的极限，自变量x可以沿x轴的正方向，负方向连续地无限增大，正因为如此，此处的N不一定要求必是正整数，仅要求N是正数即可。如（图1）当无限增大时的变化趋势。自然引出：当x→+ ∞ 时，y→0；

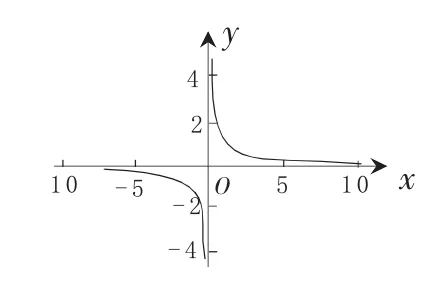
图1

当x→-∞ 时，y→0.

定性定义：设函数f（x）在x＞M（M＞0）处有定义，当x无限增大（x→+ ∞）时，对于f（x）的函数值无限接近于确定数值A，则称A为函数f（x）在x→+ ∞ 时的极限，

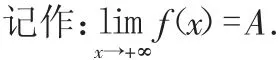
②精确定义—定量定义。

定量定义 ε—M：

设函数f（x）为定义在[a，+ ∞）上的函数，A为定数。若对任给的 ε＞0，存在正数M（≥a），使 得 当x＞M时 有 |f（x）-A|＜ε，则称函数f（x）当x→+ ∞ 时以A为极限，

当x→+∞ 时函数f（x）以A为极限意味着：A的任意小邻域内必含有f（x）在+ ∞ 的某个邻域内的全部函数值。

定义的几何意义如图 2：对任给的ε＞0，在坐标平面上平行于x轴的两条直线y=A+ε 与y=A- ε，围成以直线y=A为中心线、宽为 2ε 的带状区域。

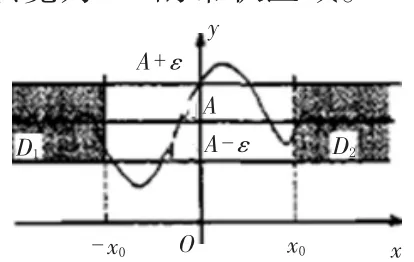
图2

例1证明

证：任给 ε＞0，取

则当x＞M时有

以下就是证明的格式模板：

证：对∀ε＞0，要使 |f（x）-A|＜ε.

……这里是解 |f（x）-A|＜ε 的过程，得结果M＞ 某个数（关于 ε 的表达式）；或当|f（x）-A|＜ε 比较繁琐不易解得，则在这里将 |f（x）-A|作适当的放大，使|f（x）-A|＜g（x），然后从g（x）＜ε 中解得x＞ 某个数。

取x= 某个数 （关于 ε 的表达式），则当x＞M时，有 |f（x）-A|＜ε 成立，

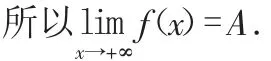
高 中 数学中 给 出 的是函 数 定 性 的 定义，只是有助于理解极限定义就可以。而在大学数学中尤其是微积分中，不仅要求理解定性定义，定量定义也可以说是微积分的“顶梁柱”。只有更加深入地理解极限ε—M，才 能 更 好 地 理 解 导 数 ，微 分 ，级 数等更深入的微积分数学。

（2）当x→x0时，函数f（x）的极限。

对函数极限而言，自变量的变化过程有很多方式。在这里仅以x→x0为例。

①直观描述—定性定义。

设函数f（x）在点x0的某个空心邻域内有定义，A为定数。如果当自变量x→x0时对应的函数值f（x）无限接近于A，则称A为函数f（x）当x→x0时 的 极 限 ，记作：

②精确定义一定量定义。

定量定义 ε- δ：

定义：设函数f（x）在点x0的某个空心邻域U°（x0；δ′）内有定义，A为定数。

若对任给的 ε＞0，存在正数 δ（＜δ′），使得当 0＜|x-x0|＜δ 时有 |f（x）-A|＜ε，

则称函数f（x）当x趋于x0时以A为极限，记作或（fx）→A。

在理解定义中，学生们的疑问有两个方面：

第一方面：定义中“函数f（x）在点x0的某个空心邻域有定义”强调的是函数f（x）在点x0的附近有定义即可，而在点x0是否有定义并不影响考察函数在该点的极限。

例2分别求f（x）=x+2 与f（x）=时的极限。

通过此例，使得学生们能够更加深入地理解“空心邻域”的意义。

第二方面：x→x0函数值f（x）无限接近于A，表示无论x是从x0左侧趋向于x0，还是从x0右侧趋向于x0，f（x），都无限接近于同一个数值A。

3.综合分析函数极限的两种。

函数极限中的 ε—M（图 3）定义中，是寻找M，使得当 |x|＞M时，使得f（x）的值都落在区域D1与D2内。与函数极限的ε- δ（图 4）定义中，是寻找 δ，当 0＜|x-x0|＜δ时，使得f（x）的值都落在某个区域内。

图3

图4

极限的 ε-N与 ε- δ 定义，虽然精确但是并未给出求极限的方法，只能用以证明某数是否为极限。证明极限问题，还是需要逐步引导。即使学生觉得理解起来困难 ，还是要 鼓励学生 ，先 在例题 的 基 础上给出类似的变式，证明过程也是类比的过程。这里也是运用了数学思想方法中的类比思想。给予学生鼓励，随着高等数学学习 的进一步深入，连续函数 、导 数、积分、无穷级数等等概念的引入，在逐步完整的实数理 论体 系 中，引 导 学 生更加 深 入 理解、体会极限思想。