单变量广义系统的能观规范型

李 莹，龚成博

（吉林师范大学 数学学院，长春130000）

0 引言

1960年卡尔曼［1］提出能观性这一控制理论中的基本概念.通常在分析或者综合一个控制系统时，都要判定该系统是否具有能观性.对多变量广义系统能控规范型和能观规范型的问题，众多学者结合控制理论对单输入单输出系统做出研究，例如，王永超等［2］完善了多变量广义系统的能观规范型问题；任夏楠等［3］阐述了非奇异变换矩阵与Luenberger能观规范型的关系，提出了将Luenberger能观规范型按照结构差异划分为广义和狭义两种规范型的观点，并且给出了完全能观线性MIMO 系统的Luenberger能观规范型实现的充要条件；王治铭等［4］对不同的规范型及辨识方法进行了统一的研究，最后得出了结构辨识与采用哪一种规范型是无关的结论；江宁强等［5］证明了在完全能控的情况下，用Luenberger 能控规范型方法进行极点配置有一定的局限性等等.但是在以上的研究中均未考虑单变量广义系统能观规范型问题.因此，本文以单输入单输出的正则广义系统为研究对象，利用受限等价变换的方法将广义系统分为快子系统和慢子系统两部分，然后给出快子系统和慢子系统能观的条件以及两个等价命题，并且得出单变量广义系统的能观规范型.

1 预备知识

对于正则的广义系统

其中：x(t)∈Rn,u(t)∈Rn和y(t)∈Rn分别为状态、输入和输出向量，对状态向量x(t)求导，记为ẋ(t)；E，A∈Rn×n，B∈Rn×m，C∈Rl×n为定常矩阵；E为奇异矩阵，且假定degdet(sE-A)=r.

首先，系统(A,B)能观的充要条件为rank[C/CA/…CAn-1]=n.考虑单输入单输出的正则广义系统（1）且rank(E)=q≤n.

如果

则称式（2）为单变量广义系统（1）的能观规范型，其中a0等于1或0.

其次，对广义系统（1）进行线性非奇异变换xˉ(t)=Q-1x(t)，可以得到

当矩阵对(E,A)正则时，总存在可逆实矩阵P和Q，使得

其中：N∈R(n-r)×(n-r)是幂零矩阵.

进而得到

这种分解通常称为快慢子系统分解，又称为第一种受限等价形式.

引理 对于广义系统（1），下述结论成立：

（3）下面两个命题等价：（a）广义系统（1）是能观的；（b）它的快子系统和慢子系统都是能观的.

2 主要结果

定理 广义系统（1）能观的充要条件是广义系统（1）受限等价于广义能观规范型（2）.

且

由引理知广义系统（1）是能观的.

如果rank(E)=n，则a0= 1，否则a0= 0.则有

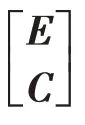
其中：g，p是行向量；g1是常数；A1是(n- 1 )×(n- 1 )阶矩阵［6］.

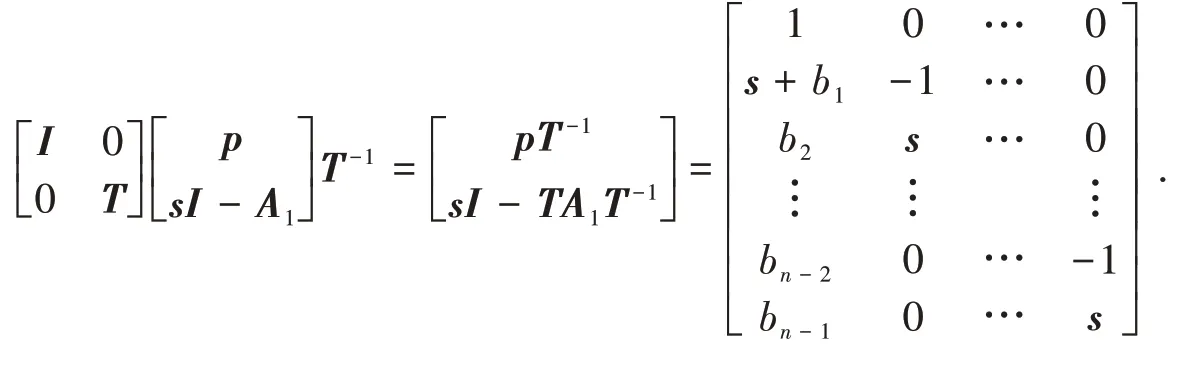
由初等变换可知，存在可逆矩阵P4和Q4，使得

3 结论

本文利用受限等价变换的方法将正则的广义系统分为快子系统和慢子系统两部分，在受限等价变换的基础上，通过引理来判断快子系统和慢子系统的能观性，并对整个系统是否能观加以判断，进而推导出单变量广义系统的能观规范型.