多时滞奇异摄动不确定离散系统的稳定性分析

王红运，张晓晗，王洪里

（吉林师范大学 数学学院，长春130000）

0 引言

20世纪初，控制科学理论的发展逐步开始，离散控制系统作为理论的一个重要分支，受到了广大学者的普遍关注［1-4］.离散控制系统理论的重要基础和基本内容是稳定性理论，即给定系统是在稳定的情况下，系统在容许范围内的不确定参数取任何值时，系统都能达到稳定的状态.为了避免不稳定的事故发生，学者们对离散控制系统的稳定性分析产生了极大的研究热情，也取得了很多的相关理论成果［5-8］.

目前，基于不确定多时滞离散系统展开的稳定性研究在理论和应用上虽然已经获得了大量的重要成果［9-11］，但是，所得结论在保守性上仍有很大的减小空间.因此，本文针对同时具有奇异摄动、不确定性、多时滞的离散控制系统的稳定性进行分析.拟定义一个新的函数，基于改进的交叉项界定方法和矩阵不等式技术，在时滞依赖的情况下，得出摄动参数上界更大的稳定性存在的结论.

1 问题描述和引理

考虑以下含有不确定性结构的奇异摄动多时变时滞离散系统

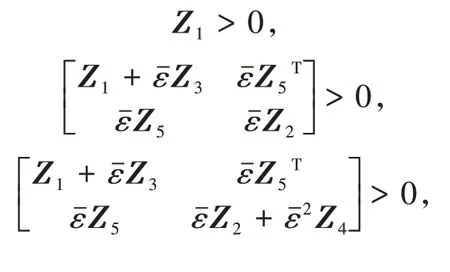
且

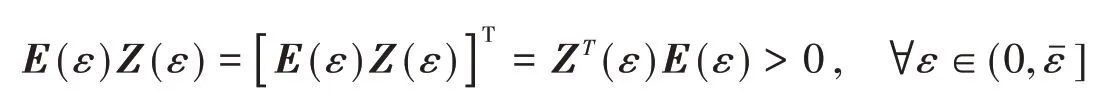
注：引理1说明了对于对称阵Zi，满足以上LMIs，则可以保证构造新的Lyapunov函数中E(ε)Z(ε)是对称正定的矩阵.

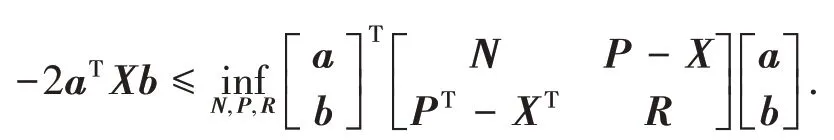
注：引理2主要针对矩阵不等式进行不同程度的放大，从而达到矩阵不等式更加稳定的目的.

2 稳定性分析

下面定理给出非线性条件的稳定性结论.

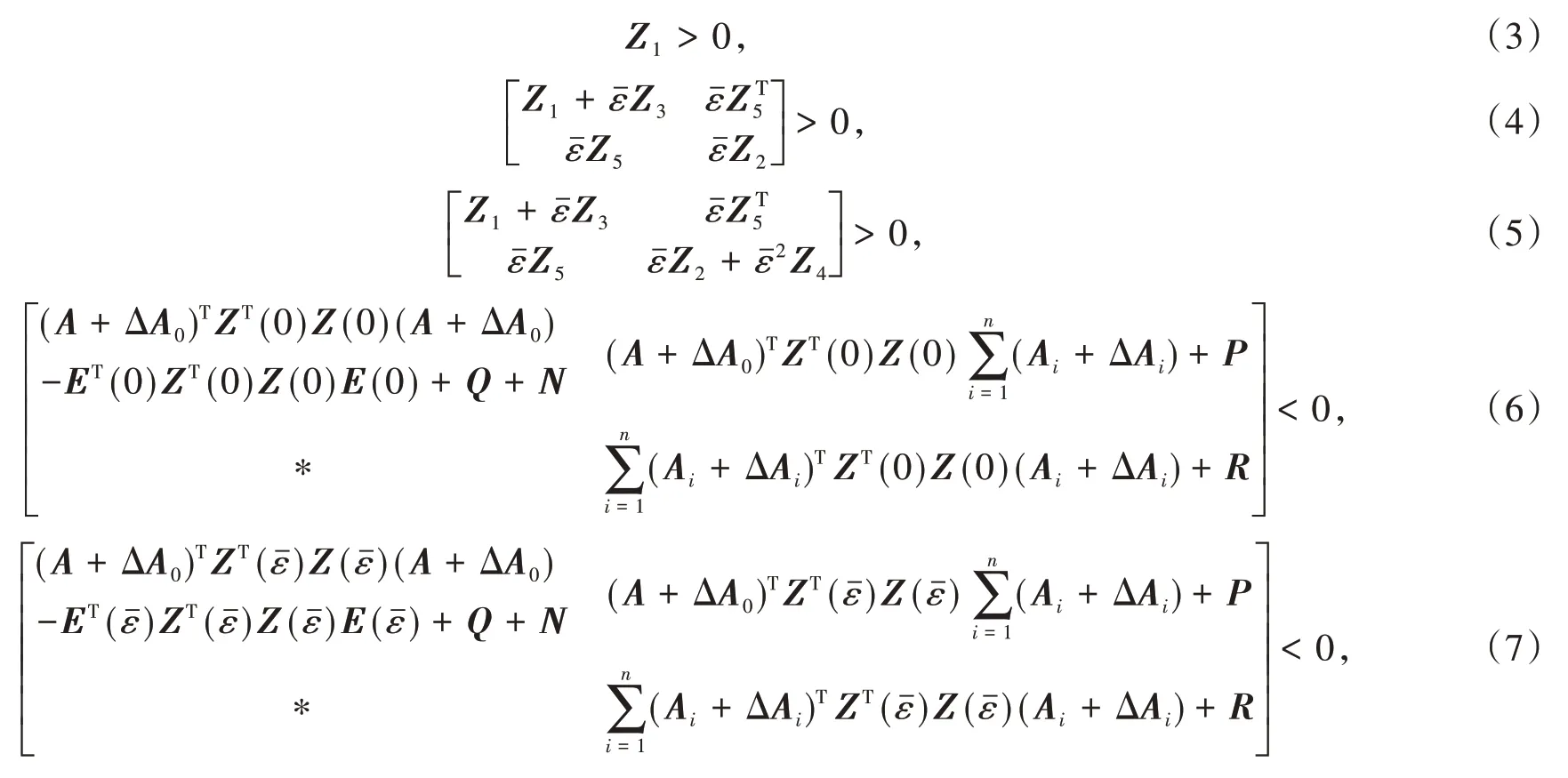
证明 构造新的Lyapunov函数V(k) =V1(k) +V2(k)，

由引理1及线性矩阵不等式（3）～（5），有

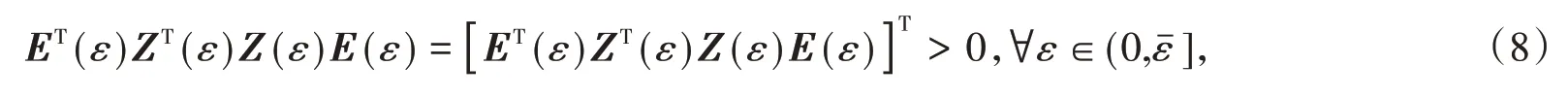
则V(k)为正定的Lyapunov函数.

将V(k)沿着系统（1）向前差分ΔV(k) =V(k+ 1) -V(k)，得

同理V2(k)沿着系统（1）向前差分得

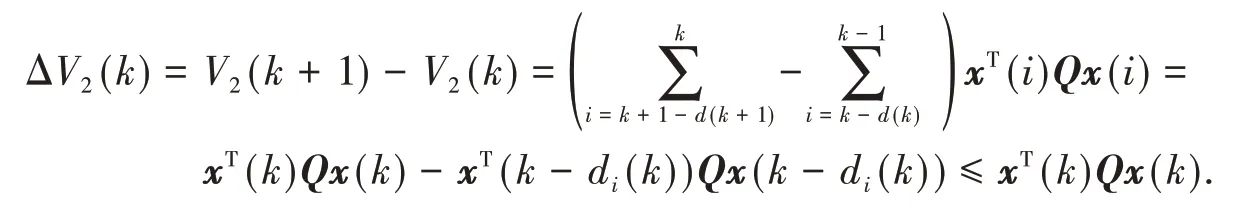
由引理2可知，存在适当维数的矩阵P，对称阵N和R，得

由上式可得

其中：η(k) =[x(k)x(k-di(k))]T；

因此，由式（6）与式（7）得G(0) ＜0，G() ＜0，利用引理1 得G(ε) ＜0,故可知V(k) ＜0,所以系统（1）是渐近稳定的.

3 结论

本文主要研究新的多时滞奇异摄动不确定离散系统的稳定性，通过设计新的Lyapunov 函数，针对时滞依赖情形的稳定性，利用相关引理、Lyapunov 稳定性理论以及新的差分不等式等交叉项界定技术，得出系统保守性更小的稳定性存在条件.