滤波误差摄动动态系统的无记忆状态反馈控制器设计

吴 越

（吉林师范大学 数学学院，长春130000）

0 引言

不确定性时变时滞奇异摄动系统源于工业生产等控制领域中的应用，现在已经成为现代控制科学的一个重要研究领域.关于系统的滤波器设计已有了比较详尽的研究，例如，文献［1］研究了含有不确定结构的时变时滞奇异摄动连续系统的滤波误差动态系统的稳定性分析问题，文献［2］得到了连续系统的时滞依赖和时滞独立两种不同情形下的滤波误差动态系统稳定性的判别条件形式等等.在上述文献中对连续系统的滤波误差动态系统稳定性分析问题的讨论较为详细，众多学者对线性时滞控制系统中的滤波器设计问题展开了研究，取得了许多成果［3-4］，但并未涉及滤波误差动态系统其他层面的研究.

本文运用线性矩阵不等式方法，主要对奇异摄动时滞滤波误差动态系统的控制器设计问题进行研究，对带有控制输入的奇异摄动时滞滤波误差动态系统，设计无记忆状态反馈控制器［5］，借助于Lyapunov稳定性理论和线性矩阵分析，构造一个新的Lyapunov 泛函，利用交叉项界定方法，推出控制器在时滞依赖和时滞独立情况下的充分性判据.

1 问题描述和引理

1.1 奇异摄动时滞滤波误差动态系统概述

首先考虑带有干扰输入的不确定时变时滞奇异摄动控制系统

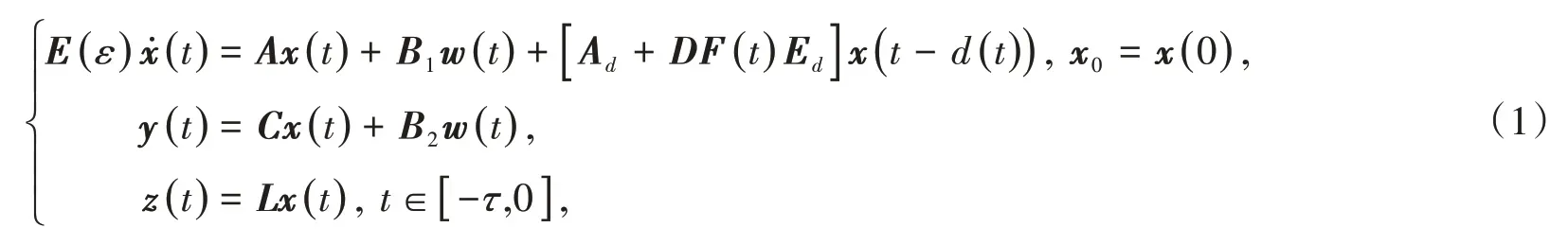
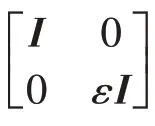
其中：τ，μ是已知实常数；F(t)∈Ri×j是范数有界的不确定系统模型参数矩阵，具有如下范数有界不确定性结构

在如下滤波器

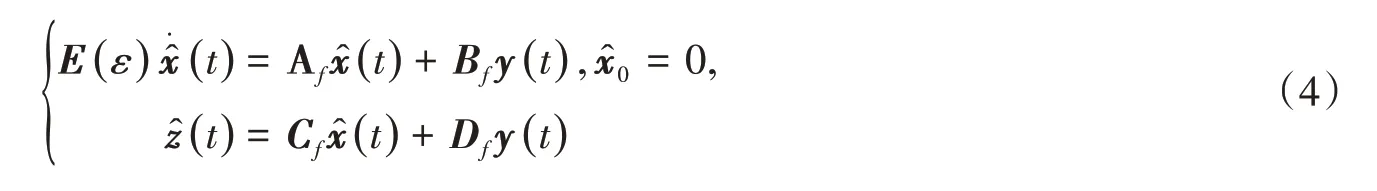
的作用下，形成如下滤波误差动态方程为

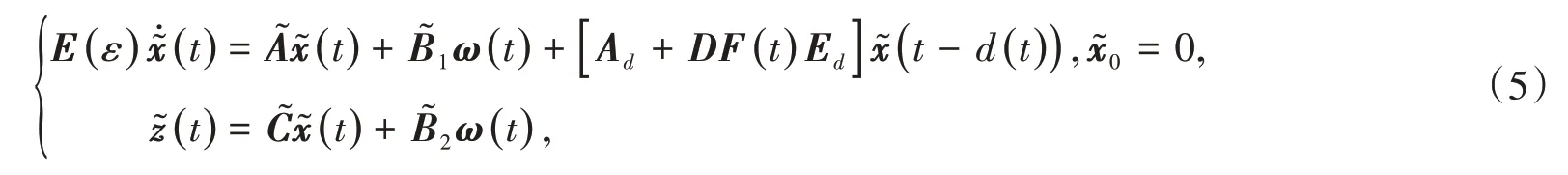
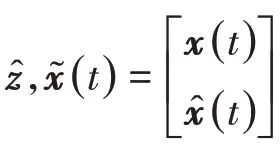
考虑带有控制输入和干扰输入的奇异摄动时滞滤波误差动态系统

其中：u(t)∈Rm是控制输入向量；B是已知的适当维数的实常矩阵.

1.2 线性不等式理论及相关引理

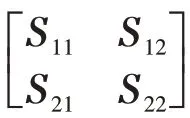
引理2［7］对于适当维数的矩阵E，D和对称矩阵Y，若不确定矩阵F(t)满足FT(t)F(t)≤I，则Y+EF(t)D+DTFT(t)ET＜0的充分必要条件是存在常数η＞0，使得Y+ηEET+η-1DTD＜0.

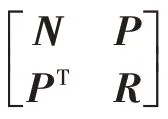
2 控制器设计

设计一个无记忆状态反馈控制器

其中：K为未知的控制器增益矩阵.则闭环系统为

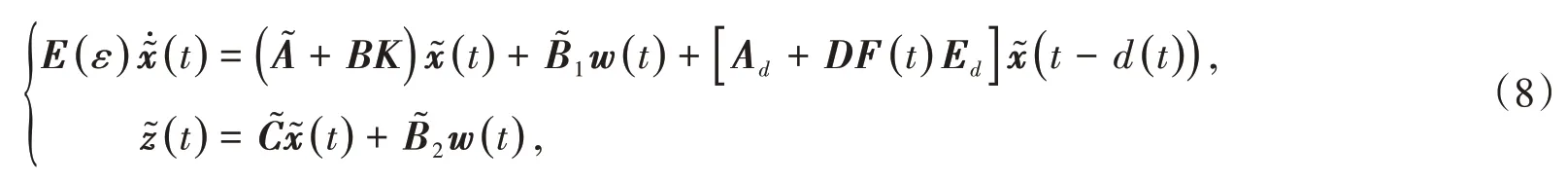
2.1 时滞依赖的控制器设计

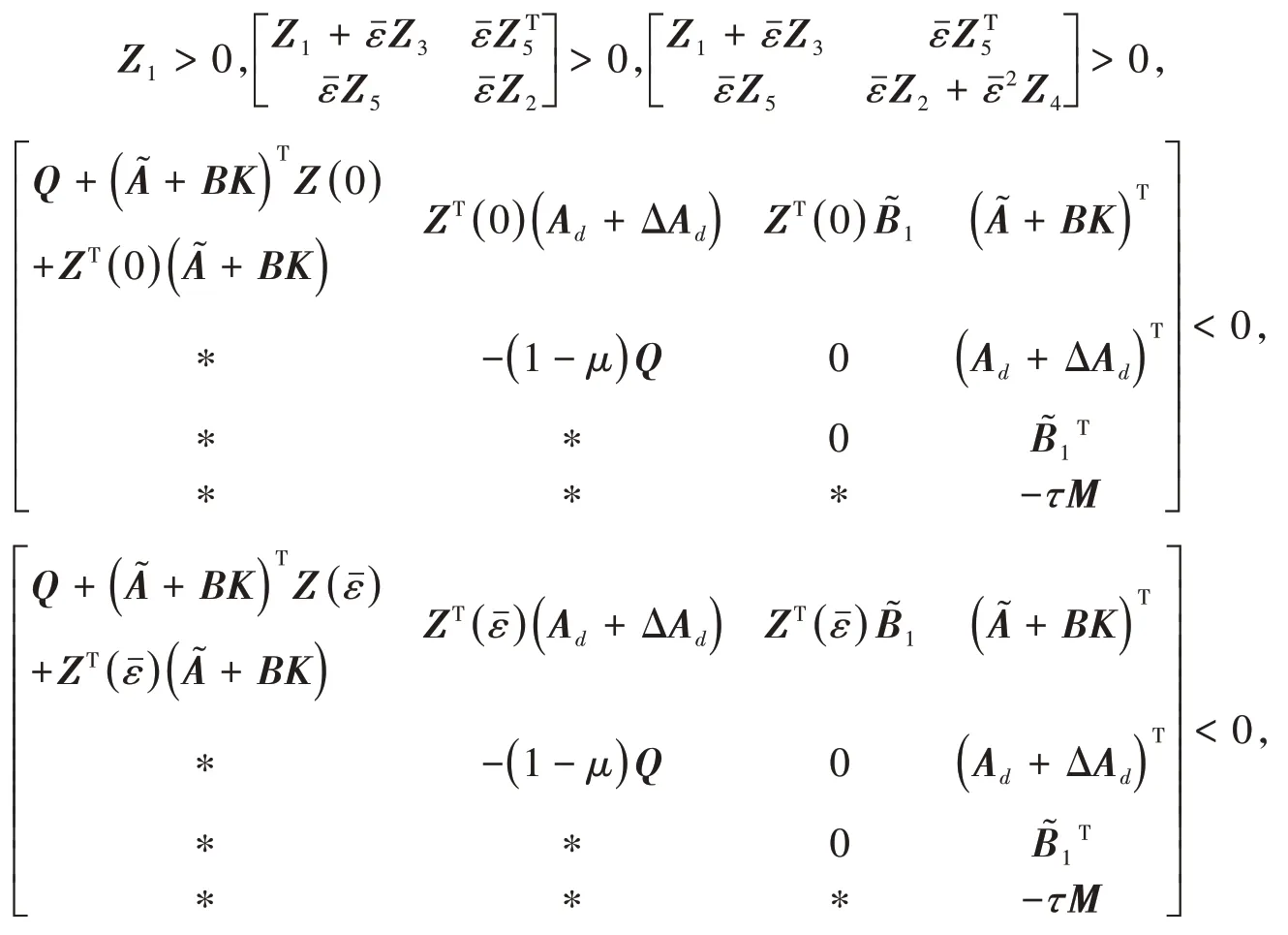
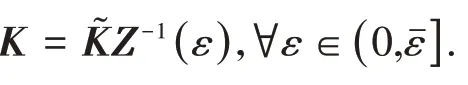
证明 构造函数V(x͂(t))=V1(t)+V2(t)+V3(t)，

其中：

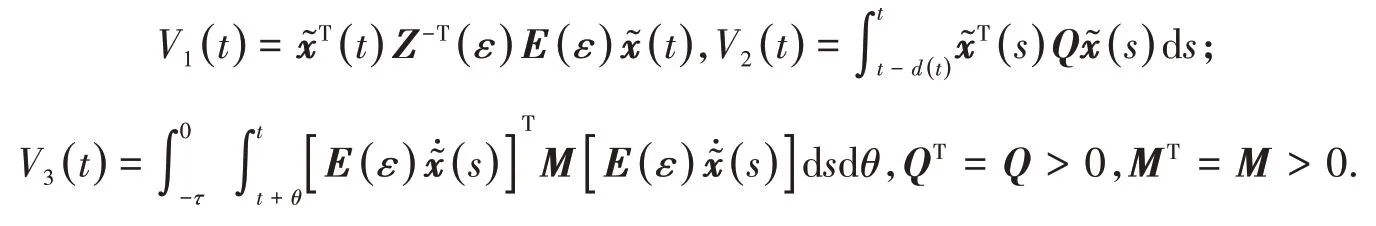
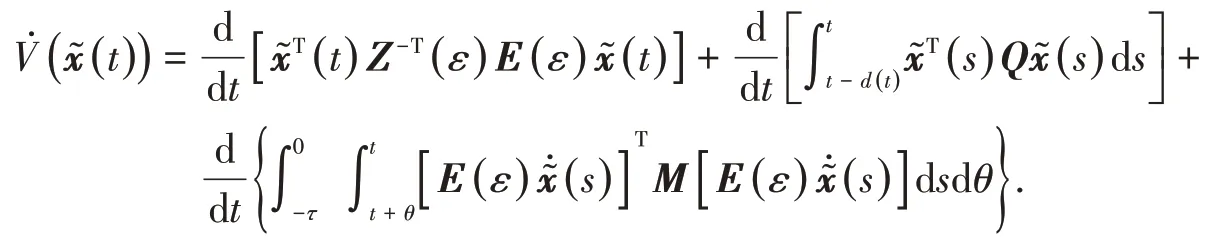
其中：

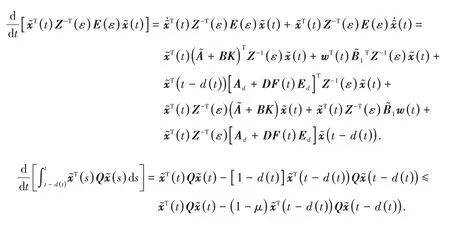
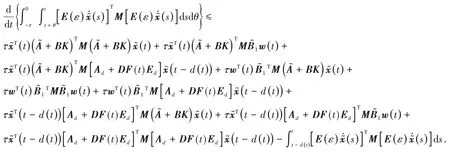
因此

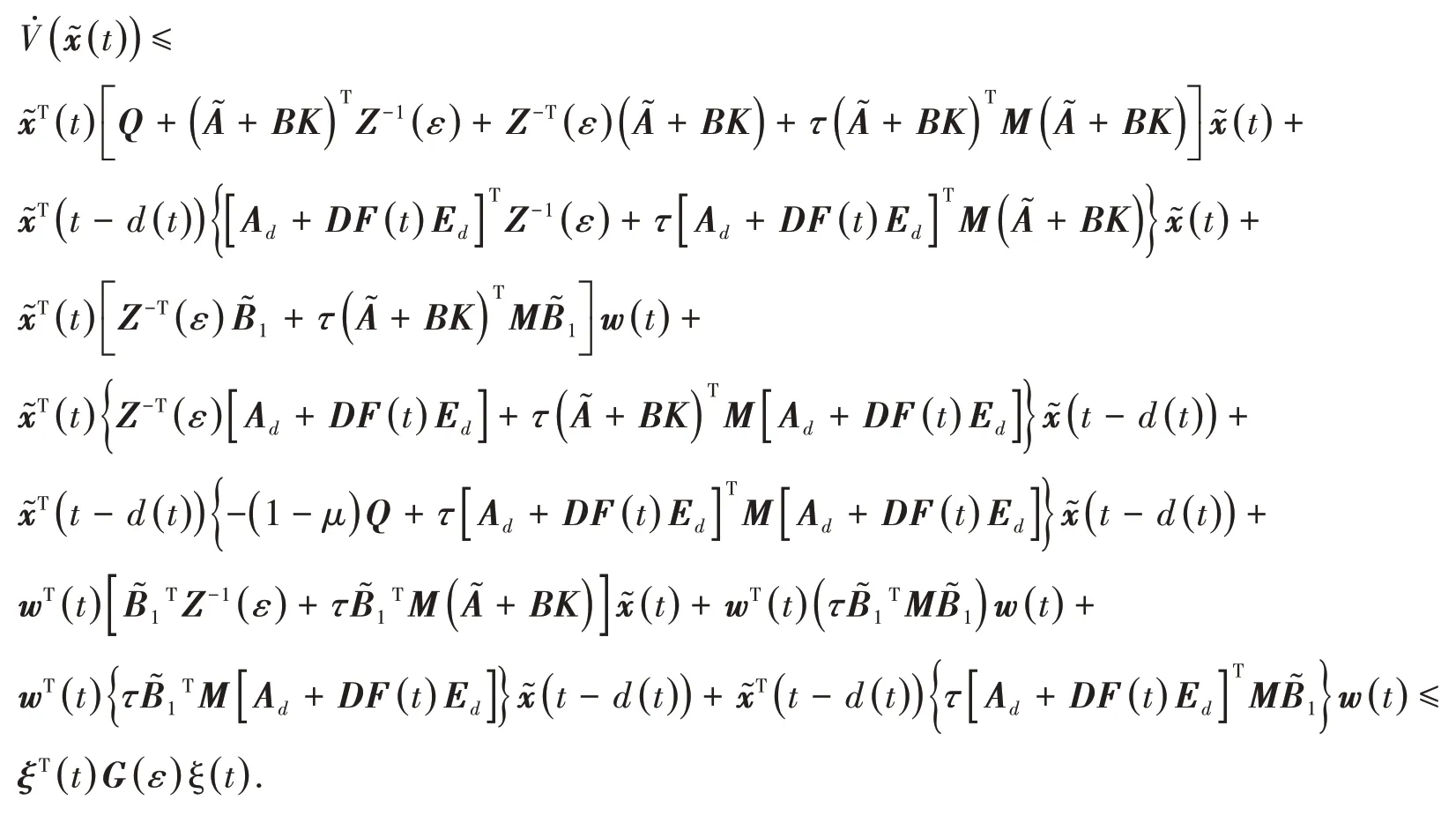
其中：

令ΔAd=DF(t)Ed，则由引理1，G(ε)＜0等价于

由线性矩阵不等式条件知，G( 0 )＜0，G()＜0.根据引理3，得G(ε)＜0，因此̇((t))＜0，根据Lyapunov稳定性理论，系统渐近稳定.

为了求得控制器参数，需要去掉不确定函数F(t)，使得G(ε)＜0.对G(ε)＜0 左乘对角矩阵diag{ZT(ε)ZT(ε)ZT(ε)}，右乘其转置，记KZ(ε)=͂，再由引理1，存在一个常数γ＞0，得

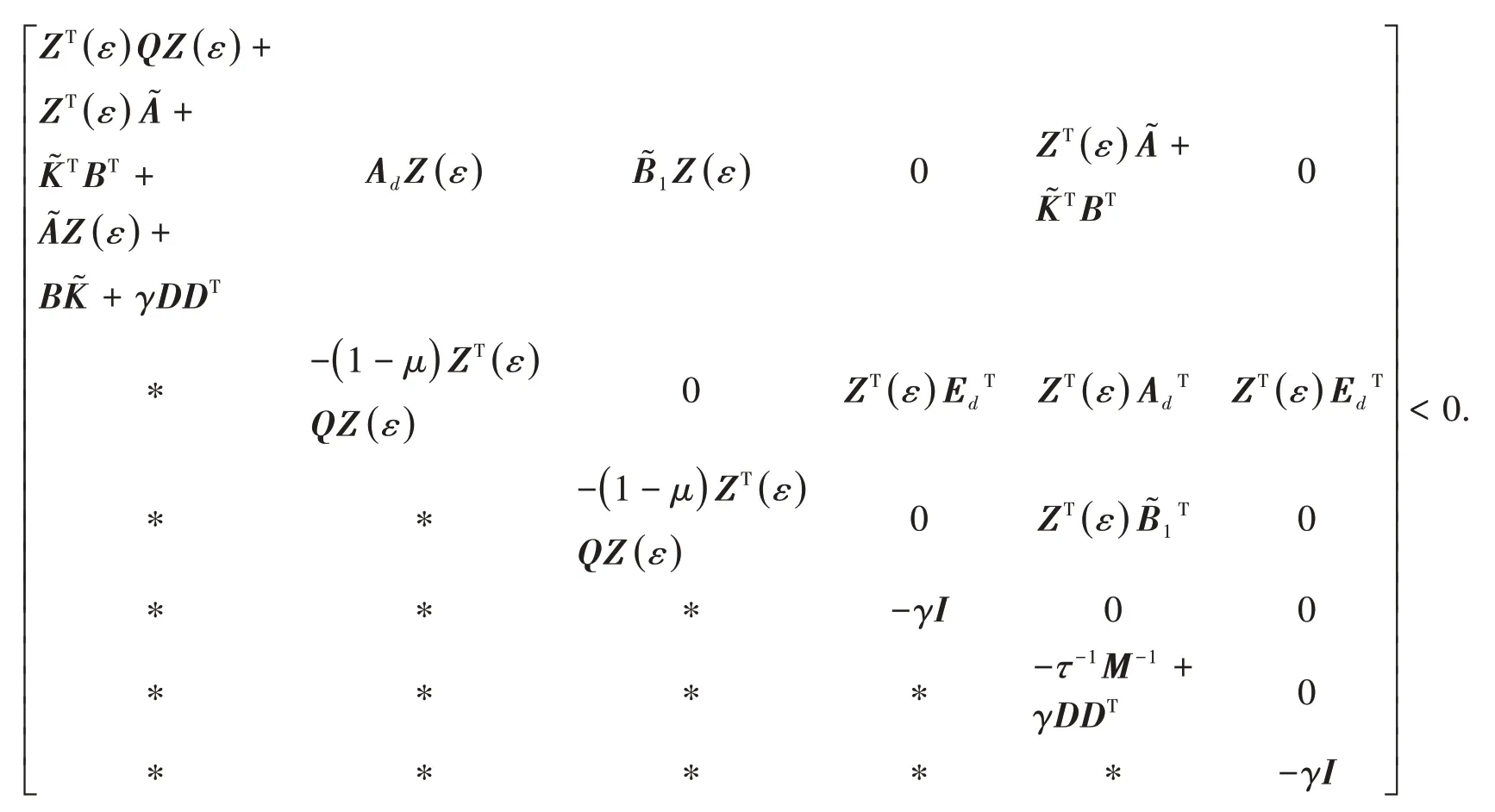
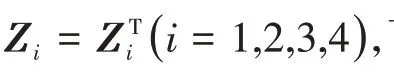
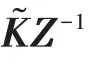
2.2 时滞独立的控制器设计

定理3 给定＞0，滤波误差动态系统对∀ε∈( 0,)是渐近稳定的.若存在对称正定矩阵Q＞0，适当维数的矩阵P，对称阵N，P，以及≥0，矩阵Zi(i= 1,2,3,4,5 )且Zi=(i= 1,2,3,4 )，使得不确定性函数满足条件( 3 )，则下列矩阵不等式条件可行

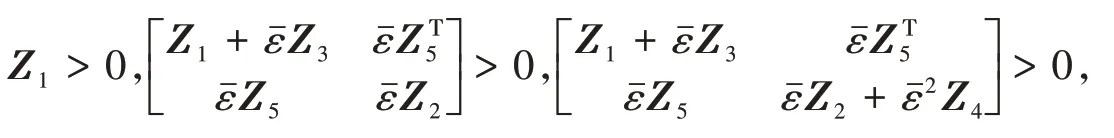
则u(t)=Kx(t)为系统( 6 )的静态状态反馈控制器，其中：K=͂Z-1(ε)，∀ε∈( 0,].

证明 构造函数V(x͂(t))=V1(t)+V2(t)，

将V((t))沿着闭环系统的任意轨迹微分，得

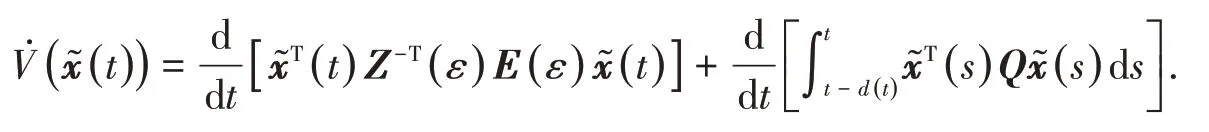
证明方法与定理1类似，故略.

定理4 给定＞0，滤波误差动态系统对∀ε∈( 0,)是渐近稳定的.若存在对称正定矩阵Q＞0，适当维数的矩阵P，对称阵N，R以及≥0，γ＞0，矩阵Zi(i= 1,2,3,4,5 )且则下列矩阵不等式条件可行

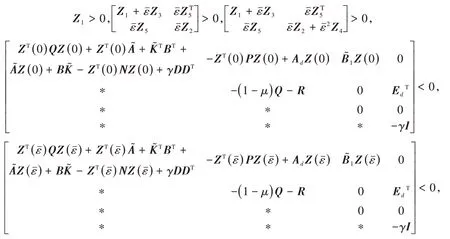
3 结论

本文对奇异摄动时滞滤波误差动态系统进行无记忆状态反馈控制器系统设计研究，构造适当的Lyapunov泛函，使滤波误差动态闭环系统渐近稳定，推出时滞依赖和时滞独立情形下的滤波误差动态系统的控制器设计定理，该系统综合性较高，尽可能减弱了时滞相关结论保守性的问题.