2021年广州中考数学压轴题解法探索及反思

广东省广州市第二中学(510530)代本富

1 题目呈现

(2021年广州中考数学第25 题)如图1,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF,DE相交于点G.

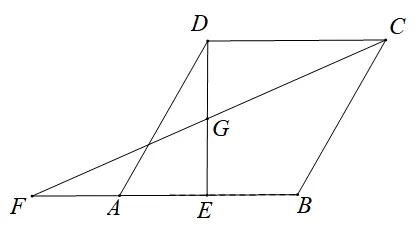
图1

(1)当点E运动到AB中点时,求证: 四边形DFEC是平行四边形;

(2)当CG=2 时,求AE的长;

(3)当点E从点A开始向右运动到点B时,求点G运动路径的长度.

2 立意分析

本题是以60°菱形为背景的中考压轴题,题目简洁,图形简单,要求明晰,内涵丰富.涉及平行四边形的判定、菱形的性质、勾股定理、相似三角形的判定和性质、定角、动点轨迹等核心知识,涉及的知识面广,要求学生积累丰富而有效的数学活动经验,才能明确解题思路,从而进行逻辑推理和运算.问题设置由易到难、层层递进,考查学生独立探究、综合分析问题和解决新问题的能力.

本题表面是学生熟悉的问题,但呈现形式及问法均有所创新,且不同层面的学生都可以尝试求解.本题第(2)问视角众多,解法多样,可以通过勾股定理列方程、“隐圆”割线定理、建立坐标系、余弦定理等方法进行解答,彰显个性.对于最难的第(3)问,大部分同学可以通过“特殊点”作图,进行轨迹猜想,能力强一点的同学可以求得正确结果,而能力更强的同学可以进行严谨的证明和说理.本题即面向全体学生,也适应学生个性发展的需要,符合课程标准所提出的使得不同的人在数学上得到不同的发展,有利于有效评价和引领教学.

完整解答本题学生要具备对数学本质的理解,需经历“操作—猜想—探究—证明”的探究过程,用较强的数学思维能力和方法,才能进行严谨的证明和说理.本题通过简单的图形考察学生数学思维,数学能力和数学方法,有效的把数学知识与数学学科核心素养有机结合、融为一体,具有良好的教学导向功能.

3 解法探究

本题第(1)问利用“一组对边平行且相等的四边形是平行四边形”即可证明,属于比较简单的问题.第(2)问和第(3)问属于较难的问题,需要学生合理添加辅助线,利用勾股定理、相似三角形等知识求解,学生在求解这两问的过程中存在一定的困难,本文主要呈现第(2)问和第(3)问的解法.

3.1 由因导果寻思路,基本图形显神威

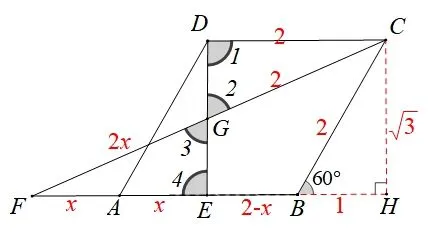
图2

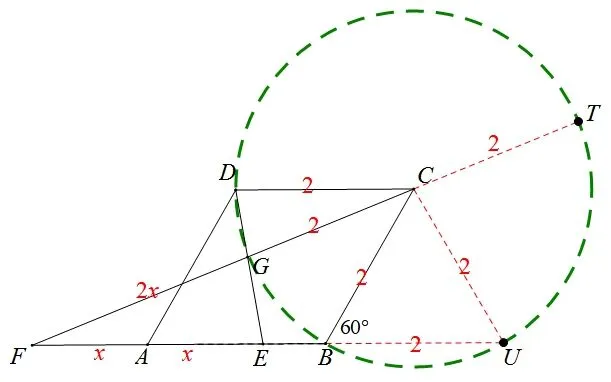
图3

3.2 合情推理觅良策,平行相似出奇招

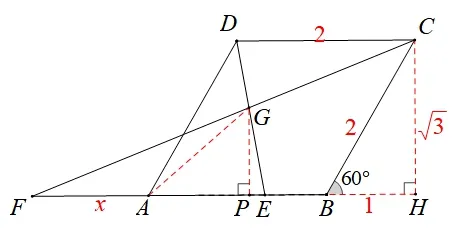
图4

图5

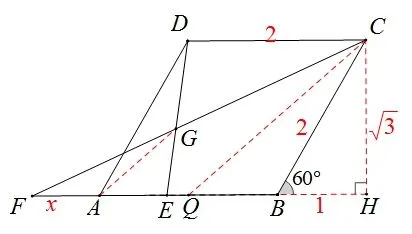
图6

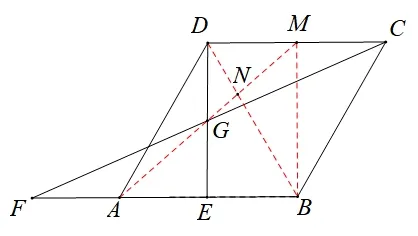
图7

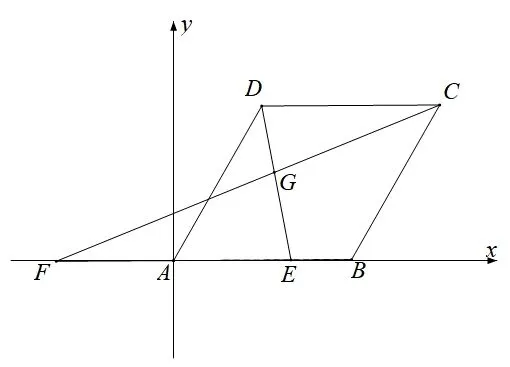
图8

3.3 解几思想细入微,引参消参轨迹现

3.4 平几问题构造难,三角运算助推理

4 解题反思

4.1 落实核心素养

《高中数学课程标准(2017年版)》明确界定“数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学的学习和应用过程中逐步形成和发展的.数学学科的核心素养包括: 数学抽象,逻辑推理,数学建模,直观想象,数学运算和数据分析”[1].

本题内涵丰富,解答本题需要综合运用平行四边形的判定、菱形的性质、勾股定理、相似三角形的判定和性质、动点轨迹等核心知识进行逻辑推理和运算,第(2)问需要学生设元进行简单的边角转化,识别并构造基本图形,进而利用方程思想解决问题;也可以运用几何直观,通过分析图形找到“隐圆”,利用割线定理进行解答; 第(3)问学生需经历“操作——猜想——探究——证明”的探究过程,用较强的数学思维能力和方法,才能进行严谨的证明和说理.本题通过简单的图形考察学生数学思维,数学能力和数学方法,有效的把数学知识与数学学科核心素养有机结合、融为一体,具有良好的教学导向功能.因此教师教学中应该尽可能的让学生理解数学的本质以及数学知识的内在逻辑关系和思想方法,提升学生的能力,发展数学核心素养,学生才能以不变应万变.

4.2 加强数学活动经验的积累

本题从简单的四边形出发,层层递进,考查学生独立探究、综合分析问题和解决新问题的能力.这些能力不是一蹴而就的,需要长期培养和渗透,需要重视知识形成的过程,加强对知识理解的活动经验的积累.《义务教育数学课程标准(2011 版)》指出:“数学活动经验的积累是提高学生数学素养的重要标志.帮助学生积累数学活动经验是数学教学的重要目标,是学生不断经历、体验各种数学活动过程的结果”[2].积累数学活动经验的目的之一是建立数学的感悟、数学的直观.日常教学重视过程教学,不仅有利于促进学生对知识的理解,更能让学生从中学会分析问题的策略、方法,体会抽象、建模、推理的基本数学思想,有利于形成策略性知识,并运用于问题的解决,这是新课标积极倡导和要求的.教师在教学中,不要过于强调解题模式,应以基础知识与基本结论为载体,重视迁移,关注过程方法和思维发展,让学生的学习能够从“方法体验”到“本质理解”再抵达“灵活应用”,为后续的学习积累丰富的数学活动经验.

4.3 重视初高中贯通培养

利用解析几何的思想和三角函数的知识对这道压轴题进行了分析和求解是常用的方法.这和“六年一贯”的培养路径相关,初高一体化管理,确保人才培养的连续性,调动整合初高中贯通培养.在初中教学时,注重挖掘初高中数学知识的衔接点,研究教学上的衔接和思维方法的衔接,积极实践在初中教学中适当融入高中知识及数学思想方法的途径;同时高中教师积极关注高中知识与初中的联系,关注学生最近发展区,在高中起始年级开设了初高衔接课程.实践表明这种初高中贯通培养模式,双向进行初高中衔接教学的路径是有效的,是利于发展学生数学学科核心素养的.