始于直观,终于直观——一道广东省中考题的教学反思

广东省东莞市万江教育管理中心(523053)温河山

1 原题呈现

如图1,边长为1 的正方形ABD中,点E为AD的中点.连接BE,将ΔABE沿BE折叠得到ΔFBE,BF交AC于点G,求CG的长.

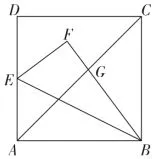
图1

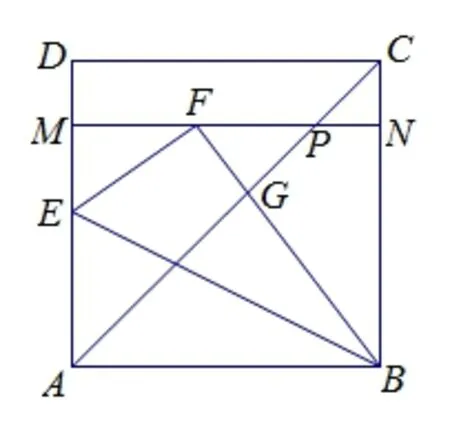
图2

2 解法探究及模型解析

2.1 原题分析

本题以正方形为背景求线段长度,包含中点、轴对称相关知识.题目条件简单,解法丰富,蕴含了丰富的几何模型.几何模型是教师借助实体或者虚拟表现来客观阐述几何形态结构的模件.几何模型作为一种“模件”虽然只是借助图形来开展教学活动,但是它指向直观思维.它根据数量关系在初中阶段常见的表现形式构造成相应图示.“几何模型”就像是符合条件的“模件”,能被快速地安装到各种几何问题中,因此,研究“几何模型”对于提升学生数学素养有很强的现实意义.

2.2 解法及模型分析

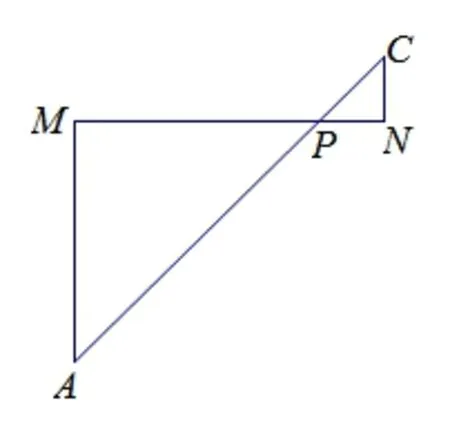
图3

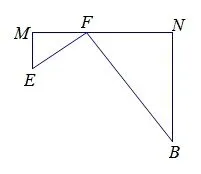
图4

图5

图6

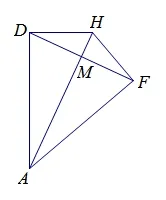
图7

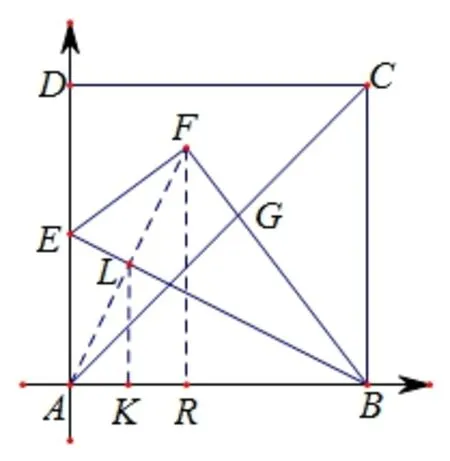
图8

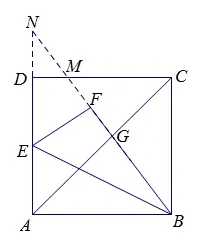
图9

图10

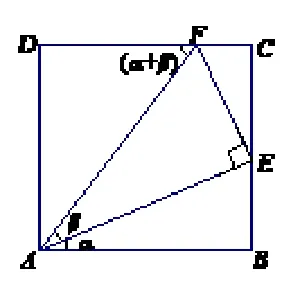
图11

3 教学反思

几何模型本质上属于直观几何的范畴,是一种通过图形所展开的数学想象能力,对看到的图形思考想象,进行合情推理,猜想可能的结论和论证思路.因此要探究几何模型渗透教学的基本路径.

3.1 课堂教学渗透法

在课堂教学中采用分类有机整合、变式、问题导向等方法将基本模型嵌入课堂中的方法称之为课堂教学渗透法.基本模型的教学应坚持课堂渗透为主,可由基本模型主动变式,通过分类等方法,有机整合教材中的例题和课后习题.

比如,学习“勾股定理”时,可渗透一线三等角模型.比如,引导学生利用图12 或者图13 推导勾股定理时,探究“一线三等角”的性质,实现从“赵爽弦图”到“一线三等角”的过渡.

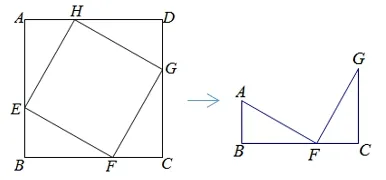
图12

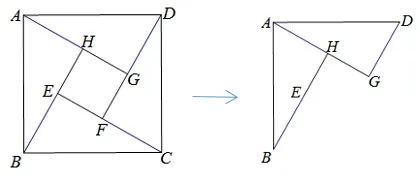
图13

3.2 课后作业渗透法

有些模型难度较大,或者需要学生先行自学,教师后续强化,这时可将基本模型放置到课后作业来完成,称之为课后作业渗透法.

如在“勾股定理”中设计课后作业:

如图14,点A的坐标为(4,3),将其绕原点O逆时针旋转90°,得到的点坐标是什么? 将点O以直线A′A作中心对称变换得到点O′的坐标是什么?

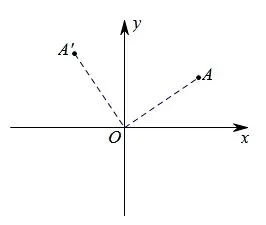
图14

3.3 后续学习伏笔渗透法

有些模型涉及的知识横跨不同年级,这时仅研究本学段相关的条件和结论,从而为后续学习,进一步挖掘相关结论埋下伏笔.

如在“一次函数”中探究:

(1)如图15,正比例函数y=ax与正比例函数相互垂直,求该正比例函数.

图15

(2)若正比例函数y=ax与正比例函数y=mx相互垂直,探究a与m的关系.

(3)过一次函数y=ax+b与正比例函数y=mx+n相互垂直,探究a与m的关系.

又如在“反比例函数”中探究:

如图16,点A在反比例函数上,点B在反比例函数上,OA⊥OB,探究OA和OB的关系.

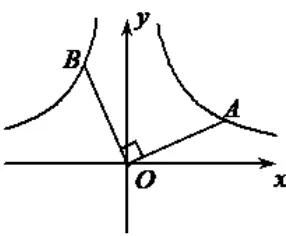
图16

在完成了几何模型的首次学习后,学生便得到了关于该模型的首次印象,包括图形及其中基本关系的猜想,而这种关系是在后续学习中常见或者必要的.在今后的学习中再次遇到该“模件”,便能在已有的基本关系上来推导其他关系,从而使得问题更快求解.正如史宁中教授所说的“思路是看出来的,不是证出来的[1]”,正所谓是“始于直观,终于直观”.