2021年北京中考几何综合题多解及变式分析*

北京亦庄实验中学(100176)章剑

1 原题呈现

(2021 北京中考第27 题)如图1,在ΔABC中,AB=AC,∠BAC=α,M为BC的中点,点D在MC上,以点A为中心,将线段AD顺时针旋转α得到线段AE,连接BE,DE.

图1

(1)比较∠BAE与∠CAD的大小; 用等式表示线段BE,BM,MD之间的数量关系,并证明;

(2)过点M作AB的垂线,交DE于点N,用等式表示线段NE与ND的数量关系,并证明.

2 解法荟萃

(1)该问相对比较常规,根据题意将线段AD顺时针旋转α得到线段AE,则AD=AE,∠DAE=α.因为∠BAC=α,则∠BAE=∠CAD.在ΔBAE和ΔCAD中,得到ΔBAEΔCAD(SAS),所以BE=CD.因为M为BC中点,则BM=CM,经过等量代换得到三条线段的关系为:BM=MD+BE,下面将运用多种方法解答第(2)问.

(2)方法1: 根据角平分线模型,构造“八字型”全等三角形

通过测量大胆假设NE=ND,接下来需要严谨证明,最常用的方法是构造全等三角形.先按照题意作图,如图2所示,由第(1)问ΔBAEΔCAD,得到∠ABE=∠C=∠ABC,结合∠ABE=∠ABC以及MH⊥AB这两个条件,联想到“垂直+ 角平分线”模型,因此延长BE交MN所在直线于点F,过D点作BE的平行线交MN所在直线于点G,辅助线如图3所示.先证明ΔFHBΔMHB,得到BF=BM,∠F=∠1,结合第(1)问的结果BM=MD+BE,则EF=BF-BE=BM-BE=(MD+BE)-BE=MD.由DG//BF,得到∠F=∠G=∠1=∠2,则ΔDMG为等腰三角形,所以MD=DG=EF.在ΔFEN和ΔGDN中,

图2

图3

所以ΔFENΔGDN(AAS),于是得到NE=ND,结论得证.当然构造“八字型”全等三角形的辅助线方法不止一种,但是思路大同小异,在此不再赘述.

方法2: 构造中位线模型

证明M点为DE中点,可以从构造中位线模型入手,如图4,在线段BM上截取BF=BE,连接EF,由方法1 可以得到∠ABE=∠ABC,又因为BF=BE,根据等腰三角形三线合一,得到AB⊥EF,由于AB⊥MH,则EF//MH,因为BM=CM,CD=BE=BF,所以MF=MD,即M为DF中点,且EF//MN,所以N为ED的中点,即NE=ND,结论得证.

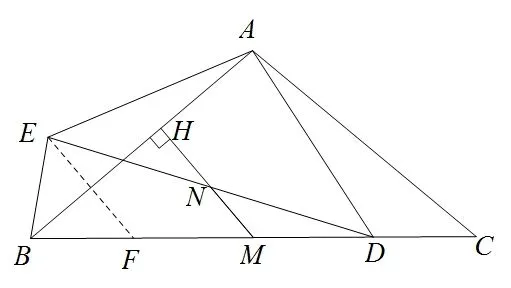
图4

图5

图6

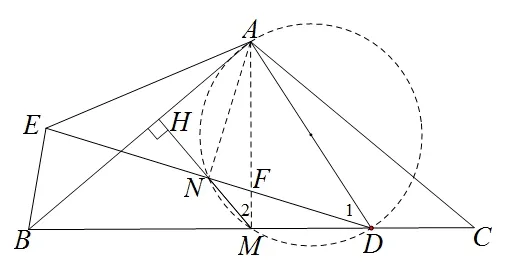
图7

3 题目变式

变式1: 当D点在线段BM上或者BC的延长线上时,结论是否仍成立?

当D点在BM上时,如图8所示,结论仍成立.在此只利用构造中位线的方法证明,其它方法读者可自行证明.在线段BM上截取BF=BE,连接EF,由方法1 可以得到∠ABE=∠ABC,又因为BF=BE,根据等腰三角形三线合一,得到AB⊥EF,由于AB⊥MH,则EF//MH,因为CD=BE=BF,所以BD=FC,又因为BM=CM,则DM=MF,即M为DF中点,且EF//MN,所以N为ED的中点,即NE=ND,结论得证.

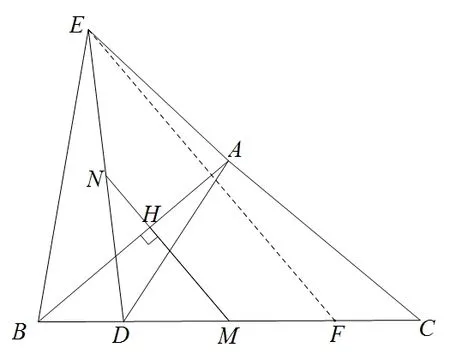
图8

图9

变式2: 交换题目条件和结论,命题是否成立?

如图10,在ΔABC中,AB=AC,∠BAC=α,M为BC的中点,点D在MC上,以点A为中心,将线段AD顺时针旋转得到线段AE,连接BE,DE.N为DE中点,连接MN,并延长MN交AB与H点,求证MH⊥AB.

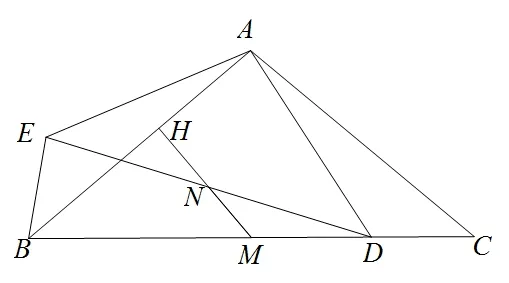
在此只采用四点共圆的方法进行求证.如图11所示,连接AN,AM,因为∠DAE=∠BAC=α,AE=AD,AB=AC,M和N分别为BC和DE的中点,所以所以A、N、M、D四点共圆,则所以∠AHM=即MH⊥AB,结论得证.

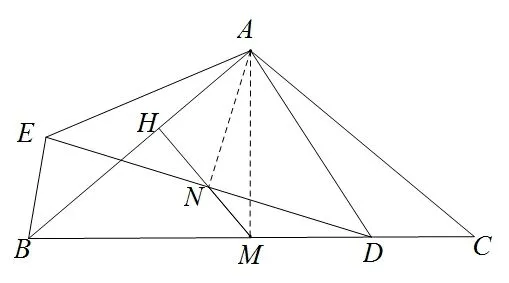
图11

变式3: 由静至动,结合轨迹和最值进行拓展

D在MC上运动时(包括M、C两个端点),当α=120°,AB=AC=2 时,其它条件不变,请指出E点和N点的轨迹,并求出EN的最小值.

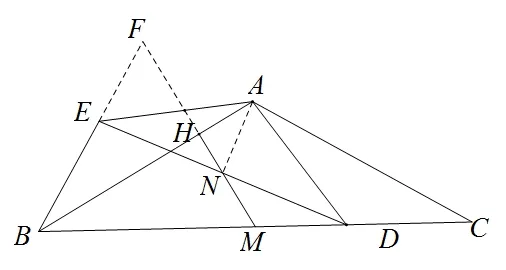
图12

2021年北京中考几何综合第27 题方法灵活多样,但是很多同学在考场仍然不得其法,原因是平时练习没有深入研究题目的本质、没有掌握基本变换的性质以及缺乏基本模型的积累.只有一题多解、一题多变,将题目作出花样,才能促使学生将知识建立内在联系,形成逻辑架构,遇到新题时,才能从旧知中迸发灵感,寻找与之契合的方法.