小波去噪后极端学习机模型在医院感染发病率预测中的应用
2022-04-23王清青范馨月查筑红
王清青,范馨月,查筑红
(1.贵州医科大学附属医院医院感染管理科,贵州 贵阳 550004;2.贵州大学数学与统计学院,贵州 贵阳 550025)
近年来,医院感染(healthcare-associated Infection,HAI)给患者和社会造成的严重经济负担已成为医学界急需解决的重大问题。医院感染不仅会提高患者死亡风险,还会延长患者的住院时间、降低病床周转率,严重影响医疗质量[1-3]。因此,建立预测模型准确预测医院感染发病率,提前采取相应防控措施,对降低医院感染发病率具有重要的现实意义。医院感染发病率常用的预测方法包括自回归移动平均滑动模型(autoregressive integrated moving average model,ARIMA)[4-6]、灰色预测模型(gray forecast model,GM)[7-9]和神经网络模型(neural network model,NNM)[10-13]等。ARIMA 模型和GM 模型使用解析模型对数据进行拟合预测,误差较大。NNM 模型易陷入局部最优解,学习效率和模型精度较低。极端学习机(extreme learning machine,ELM)模型为单隐层前馈神经网络(single-hidden layer feedforward neural networks,SLFNs),具有原理简单、训练速度快的特点[14],但数据的不平衡分布及其冗余信息产生的噪声以及离群点会对ELM的泛化能力产生影响。基于此,本研究构建了一种基于小波去噪后的ELM 模型对医院感染率进行预测分析,以期为医院感染预防与控制提供一定的参考依据。
1 资料与方法
1.1 资料来源 选取贵州省某三甲医院2014 年1 月-2019 年12 月收治的住院时间超过48 h的所有住院患者的月度医院感染发病率资料。本研究经过医院伦理委员会审核通过,患者及家属签署知情同意书。
1.2 医院感染诊断标准 参照中华人民共和国卫生部发布施行的《医院感染诊断标准》[15]。
1.3 方法
1.3.1 小波去噪后极端学习机模型 根据噪声与信号在不同频带上的小波分解系数具有不同强度分布的特点,将各频带上的噪声对应的小波系数去除,保留原始信号的小波分解系数,然后对处理后的系数进行小波重构,得到不含噪声的信号。离散型的小波变换定义为
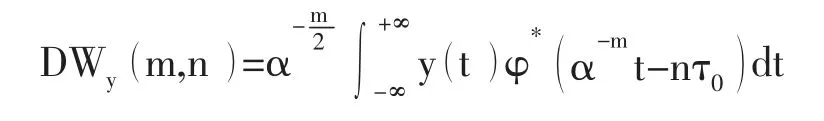
其中,m 为尺度参数,n 为平移常数,φ*为复共轭函数,φ(x)为母小波。小波去噪后的序列消除了序列的噪声对预测结果的影响。
不同的样本数据(Xi,Yi),其中X=[X1,X2,……XN]T∈RN,Y=[Y1,Y2,……YN]T∈Rm网络中含有L 个隐层节点
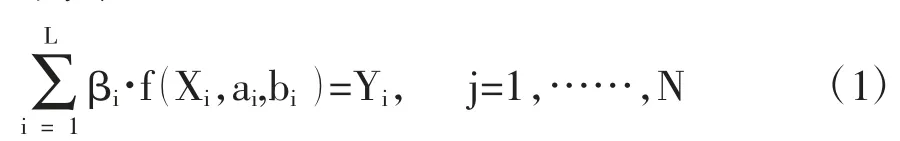
其中,αi=(αi1,αi2,……,αiN)N为连接i 个隐层节点与输入节点的输入权值向量,bi为第i 个隐层结点的偏置。βi=(βi1,βi2,……,βiN)T为连接第i 个隐层结点和输出结点的输出权值向量,f(·)为激活函数。(1)式改写为矩阵形式为:

其中,H 是隐层节点的输出,β 为输出权重,Y为期望输出。

Y=(Y1,Y2,……,YN)T,β=(β1,β2,……,βN)T,ELM的训练过程等价于求解线性方程(2),隐含层和输出层之间的连接权值β 不需要迭代调整,这也是ELM 最大的特点。ELM 输入层和隐含层的连接权值、隐含层的阈值可以随机设定,且设定完后不用再调整,ELM 结构图见图1。

图1 ELM 结构图
1.3.2 参数选择 ELM 模型中的参数有嵌入维数、隐含层神经元数、输入权重αi、神经元偏置bi和输出权值。根据预测误差确定嵌入维数和隐含层神经元数,这里取嵌入维数为2,隐含层神经元数量3。输入权重和神经元偏置在[-1,1]内随机取值,输出权重β通过求解线性方程(2)的矩阵H的Moore-Penrose广义逆得到。以2014 年1 月-2019 年6 月医院感染发病率数据作为训练样本构建小波去噪后极端学习机模型、原极端学习机模型和神经网络模型,分别对2019 年7 月-12 月该医院的医院感染发病率进行预测,并对其预测效果进行比较。用较优的预测模型对2020 年1 月-12 月医院感染发病率进行预测。
左小龙虽然在每拧下一次油门的时候都会把大帅的摩托车和自己的西风做比较,然后唏嘘,但是他依然执着的向着……不知道什么地方开去。他只是在想,他热爱自己的家园,但如果每天能做的只是发射鹅卵石,未免太过英雄气短。但他转念一想,每个人都有自己的报仇方式,有些人报仇为了报仇,有些人报仇为了悦己。况且这些不是仇恨,只是恨。
1.4 统计学分析 应用SPSS 18.0 软件进行统计分析。每年医院感染发病率之间比较采用χ2检验,P<0.05 表示差异有统计学意义。采用Matlab 2017a 软件建立小波去噪后极端学习机模型,模型精度评价采用平均绝对误差百分比(MAPE)、平均相对误差绝对值(MRE)和均方根误差(RSE)。
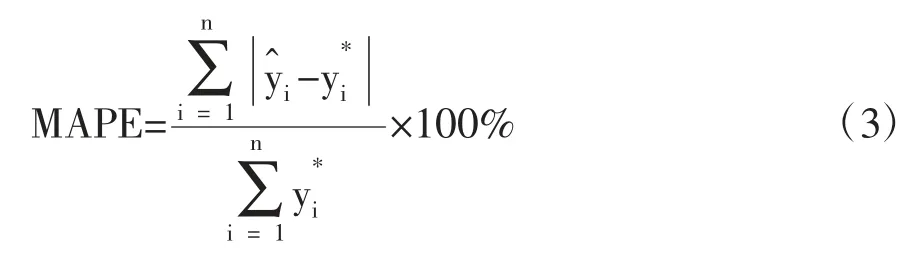
相对误差绝对值的平均值(MRE)为:
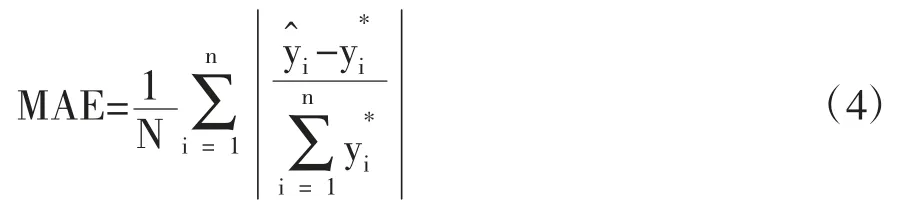
均方根误差(RSE)为:

2 结果
2.1 医院感染情况 该院2014-2019 年医院感染发病率在0.54%~2.69%,各年发病率比较,差异有统计学意义(P<0.05),且存在下降趋势(P<0.05),见图2。
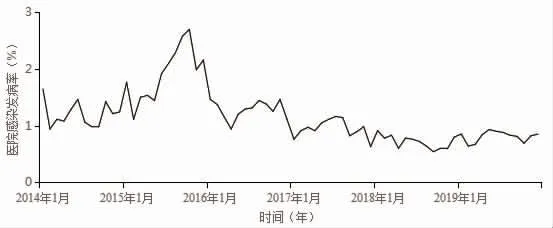
图2 2014-2019 年某院医院感染发病率变化趋势
2.2 模型识别 采用小波去噪后ELM 模型、原ELM模型和NN 模型对2014 年1 月-2019 年6 月该三甲医院医院感染发病率进行训练。小波去噪后ELM模型能较好地拟合2014 年1 月-2019 年6 月该三甲医院医院感染发病率,平均绝对误差为0.11%,均方根误差为0.01,对原始数据的拟合效果优于原ELM 模型和NN 模型,见图3及表1。
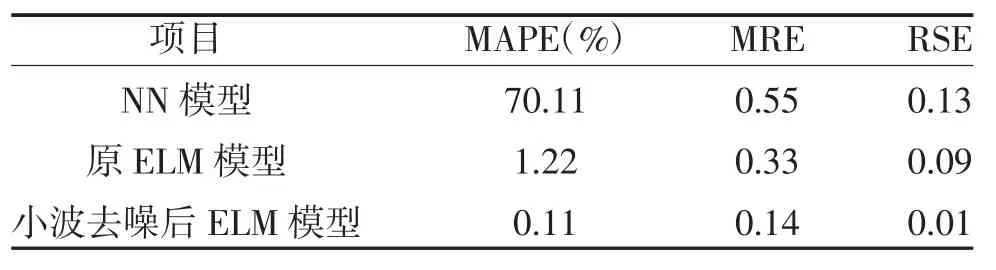
表1 三种预测模型对医院感染率拟合误差情况
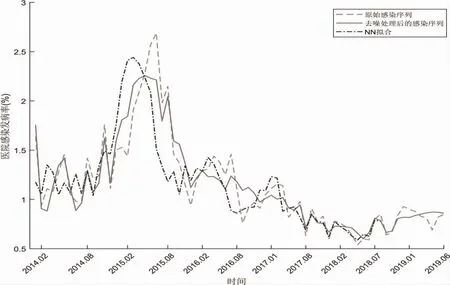
图3 三种预测模型对医院感染发病率的预测拟合效果
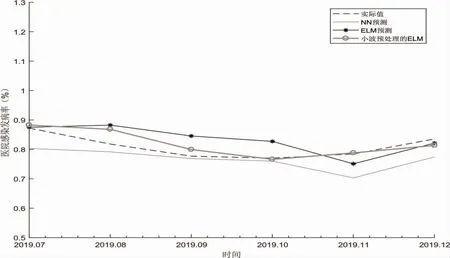
图4 三种预测模型对医院感染发病率的预测效果

表2 三种预测模型对医院感染率的预测误差
2.4 模型预测 选用小波去噪后ELM 模型对2020年1 月-12 月医院感染发病率进行预测,预测值均在95%CI范围内,见图5。

图5 小波去噪后ELM 模型对医院感染发病率的预测情况
3 讨论
医院感染作为特殊的传染性疾病,其发生、发展与医疗活动息息相关。通过医院感染发病率的前瞻性预测,不仅可以对当前采取的医院感染控制措施效果进行评价,同时还对潜在的院感暴发具有一定的预警作用。因此,基于医院感染监测数据建立准确的医院感染预测、预报体系,使医院管理者从整体上把握医院感染的趋势,从而及时调整相应的预防控制措施,已成为医院感染管理工作的重要发展方向[16-18]。
医院感染发病率受到季节、环境等因素的影响,数据变化情况较为复杂,如果作为时间序列进行处理难以用解析函数对其进行逼近,导致传统的ARIMA 模型和GM(1,1)模型拟合精度较低。对NN模型而言,由于隐函数为非线性函数,其导数值也仅仅在中心值附近呈近似线性性质,中心值的差异性导致线性关系范围的大小不同,使得NN 模型难以收敛或仅仅达到局部收敛。ELM 只有网络的隐含层节点数需要人为设定,在训练过程中输入权值及神经元偏置随机生成,具有学习和收敛速率快,拟合能力强等优点。因此,ELM 算法及其改进算法在医疗诊断[19]、疾病预测[20-22]、通信技术[23]方面都有广泛的应用。本研究构建的小波去噪后ELM 模型,有效结合了小波函数的非线性数据处理能力和极端学习机的函数逼近能力。本研究从模型的拟合精度和预测精度进行了对比分析,结果显示,小波去噪后ELM模型的MAPE、MRE 和RSE 分别为0.89%、0.01、0.02,均小于原极端学习机模型和神经网络模型,具有较好的预测效果。但是,预测的结果仍存在一定误差,可能与样本数据较少、资料所限有关。
医院感染的发生受诸多因素的影响,不同的医院环境其医院感染发病率及变化趋势也不尽相同。因此,医院感染发病率预测模型预测效果的优劣要结合医院实际情况而定,需具体研究。其次,预测模型的构建基于平时的监测数据,后续研究中为进一步提高模型预测精度,需要不断积累监测数据,对小波去噪后ELM 模型参数进行调整,从而修正或重新拟合医院感染发病率预测模型。另外,可以考虑将医院感染相关影响因素纳入模型,以便提高结果的准确性。
