由一道以新冠肺炎检测效率为背景的高考真题引发的思考

郑清勇

(山东师范大学附属中学)

分析2021年北京卷的概率试题可以发现,该题以“新冠肺炎”为背景,考查了新冠肺炎检测效率,给出了“k合1检测法”,命题新颖独特,角度较好,下面我们一起赏析这道试题.

1 真题分析

例1(2021年北京卷18)为加快新冠肺炎检测效率,某检测机构采取“k合1检测法”,即将k个人的拭子样本合并检测,若为阴性,则可确定所有样本都是阴性的;若为阳性,则还需要对本组的每个人再做检测.现有100人,已知其中2人感染病毒.

(1)(ⅰ)若采用“10合1检测法”,且两名患者在同一组,求总检测次数;

(ⅱ)已知10人分成一组,分10组,两名感染患者在同一组的概率为,定义随机变量X为总检测次数,求检测次数X的分布列和数学期望E(X);

(2)若采用“5合1检测法”,检测次数Y的期望为E(Y),试比较E(X)和E(Y)的大小(直接写出结果).

本题主要考查了离散型随机变量及其分布列、期望,考查学生的数据处理能力和应用意识、数学运算、逻辑推理.

(1)(ⅰ)若采用“10合1检测法”,每组检测一次,则共检测10次;又两名患者在同一组,需要再检测10次,因此一共需要检测20次.

(ⅱ)由题意可得X的所有可能取值为20,30.故

所以X的分布如表1所示.

表1

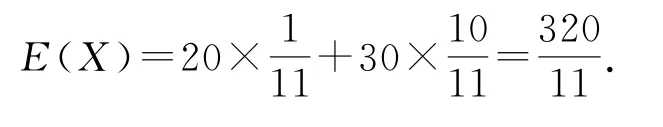
(2)由题意可得Y的所有可能取值为25,30.故

所以Y的分布列如表2所示.

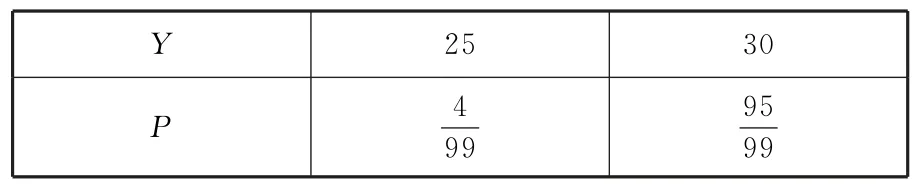
表2

综上,E(X)＜E(Y).

离散型随机变量的期望和方差应用问题的解题策略如下.1)求离散型随机变量的期望与方差的关键是确定随机变量的所有可能取值,写出随机变量的分布列,正确运用期望、方差公式进行计算.2)要注意观察随机变量的概率分布特征,若属于二项分布,则可用二项分布的期望与方差公式计算.3)在实际问题中,若两个随机变量ξ1,ξ2的期望较为接近时,就需要用D(ξ1)与D(ξ2)比较两个随机变量的稳定程度.一般地,将期望最大(或最小)的方案作为最优方案,若各方案的期望相同,则选择方差最小的方案作为最优方案.

2 反思与思考

例1给出了两种检测方法,即“10合1检测法”和“5合1检测法”,那么这里不由地会思考,是否还可以给出其他的检测方案呢?

例2若例1中采用“4合1检测法”,求检测次数Z的分布列和数学期望E(Z).

由题意可得Z的所有可能取值为29,33.故所以Z的分布列如表3所示.

表3

例3已知某医院现有4份疑似新冠肺炎病人的待检血液样本,若采用逐份检验的方式,样本检验的次数记为ζ1,若采用“4合1检测法”,样本检验的次数记为ζ2,如果E(ζ1)＝E(ζ2),求每份血液样本呈阳性的概率p(0＜p＜1).

由题意知E(ζ1)＝4,ζ2的所有可能取值为1,5,P(ζ2＝1)＝(1-p)4,P(ζ2＝5)＝1-(1-p)4,所以

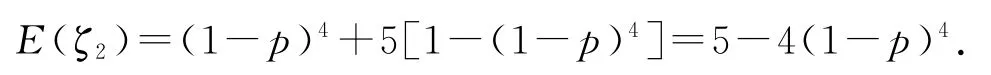
由E(ζ1)＝E(ζ2),得4＝5-4(1-p)4,解得p＝

链接练习

1.(多选题)为排查新型冠状病毒肺炎患者,需要进行核酸检测.现有两种检测方式:(1)逐份检测;(2)混合检测:将其中k份核酸样本分别取样混合在一起检测,若检测结果为阴性,则这k份核酸样本全为阴性,因而这k份核酸样本只要检测1次就够了,如果检测结果为阳性,为了明确这k份核酸样本究竟哪几份为阳性,就需要对这k份核酸样本再逐份检测,此时,这k份核酸样本的检测次数总共为k＋1次.假设在接受检测的核酸样本中,每份样本的检测结果是阴性还是阳性都是独立的,并且每份样本是阳性的概率都为p(0＜p＜1),若k＝10,运用概率统计的知识判断下列哪些p值能使得混合检测方式优于逐份检测方式(参考数据:lg0.794≈-0.1)( ).

A.0.4 B.0.3 C.0.2 D.0.1

2.党中央、国务院高度重视新型冠状病毒核酸检测工作,中央应对新型冠状病毒的感染肺炎疫情工作领导小组会议作出部署,要求尽力扩大核酸检测范围,着力提升检测能力.根据统计发现,疑似病例核酸检测呈阳性的概率为p(0＜p＜1).现有6例疑似病例,分别对其取样、检测,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则化验结果呈阳性,若混合样本呈阳性,则需将该组中备用的样本再逐个化验.若混合样本呈阴性,则判定该组各个样本均为阴性,无需再化验.现有以下三种方案.方案一:6个样本逐个化验;方案二:6个样本混合在一起化验;方案三:6个样本均分为两组,分别混合在一起化验.在新冠肺炎疫情爆发初期,由于检测能力不足,化验次数的期望值越小,则方案越“优”.

(1)若p＝,按方案一,求6例疑似病例中至少有1例呈阳性的概率;

(2)若t＝(1-p)3,现将该6例疑似病例样本进行化验,当方案三比方案二更“优”时,求t的取值范围.

链接练习参考答案

1.CD.

提示:若混合检测方式,样本需要检测总次数Y的可能取值为1,11.因此

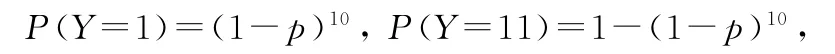
故Y的分布列如表4所示.

表4

若逐份检测方式,样本需要检测总次数X,则E(X)＝10,要使得混合检测方式优于逐份检测方式,需E(Y)＜E(X),即11-10×(1-p)10＜10,即1-p＞10-0.1.

又lg0.794≈-0.1,所以1-p＞10lg0.794＝0.794,p＜1-0.794＝0.206,所以0＜p＜0.206.

2.(1)用X表示6例疑似病例中化验呈阳性的人数,则随机变量X～B(6,),由题意可知P(x≥1)＝1-P(x＝0)＝1-6 例疑似病例中至少有1 例呈阳性的概率为

(2)方案二:混合一起检验,记检验次数为ξ,则ξ的可能取值为1,7,所以P(ξ＝1)＝t2,P(ξ＝7)＝1-t2,则E(ξ)＝t2＋7(1-t2)＝7-6t2.

方案三:每组的三个样本混合在一起化验,记检验次数为η,则η的所有可能取值为2,5,8,所以

(完)