增强六个解题意识,有效备考立体几何

刘海涛

(安徽省芜湖市第一中学)

由于立体几何问题能有效考查学生直观想象、逻辑推理、数学建模、数据分析、数学运算、数学抽象等数学核心素养,它已经成为近些年高考的一大亮点和热点,常考常新.立体几何问题常与其他知识融合、渗透,且常以数学文化或实际问题为背景命题,情境新颖,题干冗长,学生往往不易读懂题意,难以将实际问题抽象成数学问题.纵观近几年的高考题及各级各类模考题,立体几何一般稳定在两小题一大题,分值约占总分的15%,考查态势基本稳定,主要考查空间几何体的结构、表面积、体积,空间中点、线、面位置关系的证明,空间中的角与距离等知识.解决此类问题首先需要读懂题目所叙述的实际情境或文化背景,抽象出空间几何体所属模型,最后利用函数、方程(组)、不等式(组)、平面几何的动点轨迹等知识解答.因此,在立体几何的复习中,必须强化阅读理解意识、模型意识、函数意识、方程(组)意识、不等式意识及动点的轨迹意识.下面通过六道典型例题,浅谈在立体几何的复习备考中,增强以上六个意识的重要性,以供读者参考.

1 阅读理解意识

以数学文化或实际问题为背景命制的立体几何问题,通常题目文字叙述较长、数据较多,需要学生具有良好的阅读理解、数据分析及数学抽象概括能力,审题时要把握好题目的关键条件、注意挖掘隐含信息.

例1我国南北朝时期的著名数学家祖暅提出了祖暅原理:“幂势既同,则积不容异.”意思是,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等.运用祖暅原理计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图1-甲)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图1-乙),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等,即＝πR2·R-·R＝.现将椭圆＝1绕y轴旋转一周后得一橄榄状的几何体(如图1-丙),类比上述方法,运用祖暅原理可求得其体积等于( ).

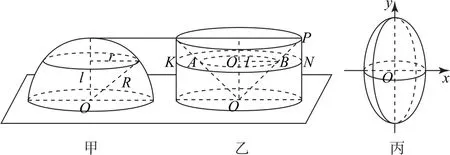
图1

A.32π B.24π

C.18π D.16π

构造一个底面半径为2,高为3的圆柱,在圆柱中挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,设截面与顶点距离为h(0≤h≤3)时,小圆锥的底面半径为r,则即r＝,所以截面面积为4π-

把y＝h代入＝1,解得x2＝,则橄榄球形几何体的截面面积为πx2＝4π-,由祖暅原理可得橄榄球形几何体的体积为

故选D.

解答该题的关键是读懂题意,对于不知道体积公式的几何体,通过构造同高等底半径的圆柱且从内部挖去适当的圆锥的空间几何体,继而计算得到高相等时截面面积相等,根据祖暅原理求得待求几何体的体积.

2 模型意识

在解决立体几何问题时,对于题中给出特殊条件的空间几何体,我们往往可以借助特殊空间几何体予以分析,如求空间几何体的外接球问题,对于满足三条棱两两垂直或三组对棱分别相等的三棱锥,我们可以将其顶点放入符合条件的长方体中,用长方体模型求其外接球.在复习备考中,我们要熟记一些特殊的空间几何体模型,解题时尝试用特殊模型辅助分析往往可简化解题过程,达到事半功倍的效果.

例2在平行四边形ABCD中,AB＝BC＝3,cosA＝,以BD为折痕,将△BDC折起,使点C到达点E处,且满足AE＝AD,则三棱锥E-ABD的外接球的表面积为________.

在△ABD中,由余弦定理得BD2＝AD2＋AB2-2AD·AB·cosA＝9,即BD＝3,则AE＝AD＝BD＝BE＝3,DE＝AB＝,则三棱锥E-ABD的每组对棱长分别相等.又因为长方体的面对角线可构成三组对棱长分别相等的三棱锥,设长方体的长、宽、高分别为a,b,c,不妨设＝3,所以该长方体的外接球即为三棱锥E-ABD的外接球,所以外接球的半径为

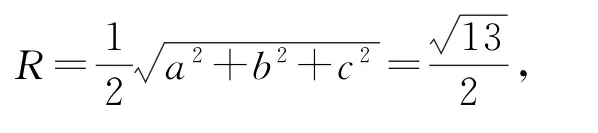
若用几何法找球心,再求半径,过程复杂,运算量大,而根据三棱锥的三组对棱长分别相等的几何特征,将其放入长方体模型中考虑外接球问题,思路自然流畅,解答过程简捷易懂.

3 函数意识

立体几何题中有关求值(最值、范围等)的问题,通常要选取变量(角度、线段长度、线段比值等)构建函数关系式,将问题转化为求函数值(最值、值域等).

例3如图2所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SCD⊥底面ABCD,△SAB是边长为2的等边三角形,点P,Q分别为侧棱SA,SB上的动点,记s＝DP＋PQ＋QC,则s的最小值的取值范围是________.

图2

由底面ABCD为矩形得BC⊥CD,又平面SCD⊥平面ABCD,平面SCD∩平面ABCD＝CD,BC⊂平 面ABCD,所 以BC⊥平 面SCD,又SC⊂平 面SCD,则BC⊥SC.同理可得AD⊥SD,又AD＝BC,SA＝SB,所以△SAD≌△SBC,则SC＝SD.将侧面SAD,SAB,SBC展开后,展开图如图3所示,则s的最小值的取值范围即为CD的取值范围.

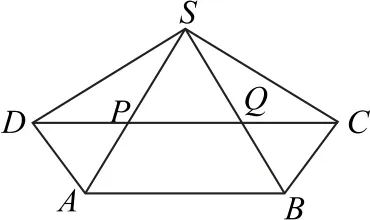
图3

求解侧面上的线段长之和的最小值问题时,利用侧面展开图,根据两点之间线段最短,确定最小值.由于本题中线段长度不定,涉及最小值的取值范围求解,我们需利用某一变量表示出所求的最小值,故考虑将问题转化为求解函数的值域问题.本题因涉及平面几何,故采用三角函数与解三角形的知识来求解相对简单,用三角函数表示出所求线段长后,再利用三角恒等变换知识化简,最终转化为正弦型函数值域的求解问题.

4 方程(组)意识

在立体几何问题中,有些已知线面角或二面角大小,探究点的位置关系或线段长度问题因涉及一个或多个变量,无法建立函数关系,这时可以通过方程(组)建立相应关系,再根据题意进行解答.

例4如图4-甲所示,在梯形ABCD中,AD∥BC,∠ABC＝90°,点M,N分别在边AB,BC上,沿直 线MD,DN,NM分别将△AMD,△CDN,△BMN折起,点A,B,C重合于一点P,得到如图4-乙所示的三棱锥P-MND.

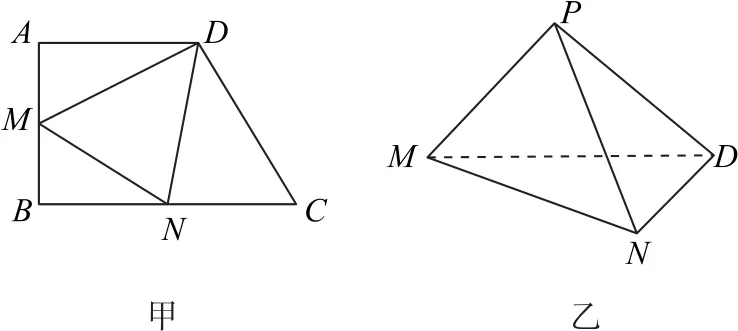
图4

(1)证明:平面PMD⊥平面PND;

(2)若cos ∠DNP＝,DP＝5,求直线DP与平面DMN所成角的正弦值.

(1)略.

(2)由题意得MA＝MB＝MP,NB＝NC＝NP,AD＝DC＝DP.设AM＝a,BN＝b,如图5-甲所示,作DH⊥BC,则

图5

因为该题涉及的线段长度较多,所以考虑设AM＝a,BN＝b,通过几何关系的分析得到方程组,解出a,b的值,从而算出所求线面角,体现了立体几何计算中的方程组意识.

5 不等式意识

立体几何题中遇到求取值范围、最值,比较大小、证明不等关系等问题时,除了构建函数关系式解题,有时借助不等式能更快地解决问题.

例5已知三棱锥P-ABC的顶点P在底面的射影O为△ABC的垂心,若S△ABC·S△OBC＝,且三棱锥P-ABC的外接球半径为3,则S△PAB＋S△PBC＋S△PCA的最大值为_________.

如图6 所示,连接AO并延长交BC于D,由题意知AD⊥BC,又PO⊥平面ABC,BC⊂平面ABC,所以PO⊥BC,PO∩AD＝O,

图6

所以BC⊥平面PAD,所以BC⊥PA,BC⊥PD.同理可证PC⊥AB,PB⊥AC.由S△ABC·S△OBC＝得AD·OD＝PD2,即又∠PDO＝∠PDA,所 以△POD∽△APD,则∠APD＝∠POD＝90°,所 以PA⊥PD,又PA⊥BC,BC∩PD＝D,所以PA⊥平面PBC,PA⊥PB,PA⊥PC.又PC⊥AB,PA∩AB＝A,所以PC⊥平面PAB,所以PC⊥PB,则PA,PB,PC两两互相垂直,所以三棱锥P-ABC的外接球是以PA,PB,PC为棱的长方体的外接球.又三棱锥P-ABC的外接球半径为3,则PA2＋PB2＋PC2＝36,则

本题考查三棱锥的结构特征、空间垂直关系的相互转化、多面体外接球半径的求法,解答该题的关键是得到三棱锥三条侧棱两两垂直,从而利用长方体模型求出外接球半径.

6 动点的轨迹意识

立体几何问题中,对于一些与动点有关的取值范围或最值问题,若能从平面解析几何角度分析,得出动点的轨迹方程,则可以将空间问题平面化.

例6如图7 所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AB∥CD,AB⊥AD,CD＝AD＝＝2,PA＝3,若动点Q在△PAD内及边上运动,使得 ∠CQD＝∠BQA,则三棱锥Q-ABC的体积最大值为_________.

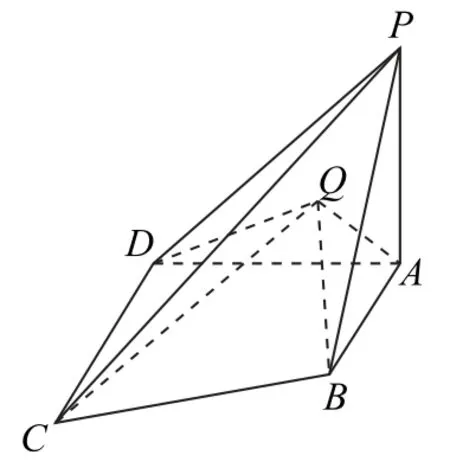
图7

因为PA⊥平面ABCD,PA⊂平面PAD,所以平面PAD⊥平面ABCD,因为AB⊥AD,平面PAD∩平面ABCD＝AD,AB⊂平面ABCD,所以AB⊥平面PAD,又AB∥CD,所以CD⊥平面PAD.因为Q在△PAD内及边上,所以AB⊥QA,CD⊥QD,所以tan∠CQD＝,tan∠BQA＝因为∠CQD＝∠BQA,所以,因 为CD＝,所以QD＝.在平面PAD内,以DA的中点为原点,线段DA的垂直平分线为y轴,建立平面直角坐标系xOy(如图8),则D(-1,0),A(1,0),P(1,3).设Q(x,y),由QD＝,得

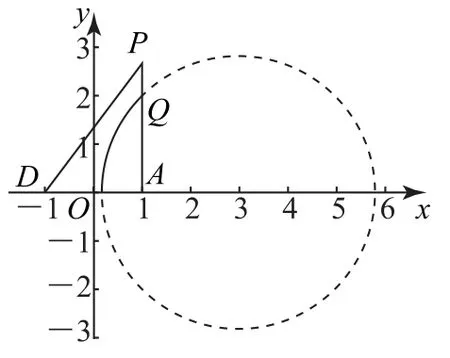
图8

整理得(x-3)2＋y2＝8,所以点Q的轨迹是圆(x-3)2＋y2＝8,在△PAD的边上或内部的圆弧如图8所示.当点Q为圆与线段PA的交点时,点Q到DA的距离最大,令x＝1,解得|y|＝2,则点Q到DA的距离最大值为2,此时Q在PA上.

通过以上六道例题,不难发现,立体几何问题既可能以数学文化或实际问题为背景,也可能以具体的空间几何体为模型命题,且往往与其他知识相融合,使得其既具有基础性和综合性,又具有应用性和创新性.因此,我们在复习备考中,一方面要加强相应的思想方法的训练,如数学建模思想、化归与转化思想等;另一方面要注重解题意识的培养.

(完)