2021年高考全国乙卷理科数学第11题解法探究

陈晓明

(安徽省宁国中学)

解析几何是高中数学重要的内容,解析几何问题一般综合性强,运算量大,如何寻找解析几何问题的本质、优化其运算的路径,具有非常现实的意义.笔者以2021年高考全国乙卷理科数学第11题为例,对其解法进行探究,以期抛砖引玉.高考复习备考中应当多花点精力研究高考题,只有把这些高考题做熟练、分析透彻,才能触类旁通,高考数学复习归根结底还是要落实数学核心素养的提升.

1 真题再现

题目(2021年全国乙卷理11)设B是椭圆C:＝1(a＞b＞0)的上顶点,若C上的任意一点P都满足|PB|≤2b,则C的离心率的取值范围是( ).

2 解法探究

思路1要求椭圆离心率e的取值范围,只需构造关于椭圆的特征量a,b,c的不等式,显然以题目中的条件“C上的任意一点P都满足|PB|≤2b”为突破口,设点,利用两点间的距离公式构造不等式,利用椭圆方程消元,从而将问题转化为二次函数在闭区间的最值问题,这是高考的高频考点.

化简得(c2-b2)2≤0,显然当b2＜c2时该不等式不成立.故这种情况不存在.

综上,椭圆C的离心率的取值范围是,故选C.

图1

图2

其实,由1)可知,当y0＝-b时,|PB|2的值为4b2,而2)中关于y0的二次函数在[-b,]上单调递增,所以条件|PB|≤2b显然不成立,故这种情况肯定不存在.

思路2如果用参数方程表示椭圆上的点,就可以利用三角函数的有界性解决问题,从而避开利用椭圆方程消元的复杂性.

解法2(参数方程)设P(acosθ,bsinθ),θ∈[0,2π),因为B(0,b),且对任意一点P都满足|PB|≤2b,所以(acosθ)2＋(bsinθ-b)2≤4b2对任意θ∈[0,2π)恒成立,即

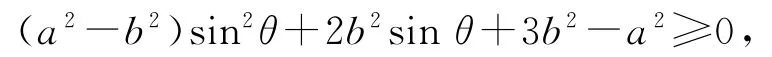
对任意θ∈[0,2π)恒成立.令sinθ＝x(x∈[-1,1]),f(x)＝c2x2＋2b2x＋3b2-a2,则原问题转化为对任意x∈[-1,1],f(x)≥0恒成立.因为抛物线开口向上,且f(-1)＝0,所以只需-≤-1(对称轴在区间左)即可,故b2≥c2,解得e∈,故选C.

由题设“C上的任意一点P都满足|PB|≤2b”知该问题实质上是一个恒成立问题,通常可转化为函数的最值问题.相对于解法1,解法2的计算稍微要简单些,主要是引入参数方程及采用换元法.对比两种解法,不难发现,它们在本质上是完全一致的.二次函数在闭区间的最值问题一直是高考的热点,此类问题主要包括四种情况:轴定区间定(二次函数的对称轴和定义域都不含参数)、轴定区间动(只有定义域区间端点含参数)、轴动区间定(只有二次函数的对称轴含参数)、轴动区间动(二次函数的对称轴和定义域区间端点都含参数).因为第一种情况较简单,第四种情况较复杂,所以考得较少,而中间两种情况考得特别多.轴动区间定的情况只需分三种情况讨论(对称轴在区间左、中、右)即可,本解法即属于这种情况,而且恰有f(-1)＝0,所以要使f(x)≥0恒成立,只可能轴在区间左,这样问题变得简化.

思路3求离心率的取值范围,只需构造关于椭圆的特征量a,b,c的不等式,在设出椭圆参数方程后,可尝试运用分离参数式法,得到关于a,b的不等式.

解法3(分离参数式)由解法2知(acosθ)2＋(bsinθ-b)2≤4b2对任意θ∈[0,2π)恒成立,整理得a2cos2θ≤(3-sin2θ＋2sinθ)b2,易知当θ＝时不等式成立,故只需

这种分离参数式(含有参数的式子)法直接,易懂,对参数式分子、分母分别进行因式分解,化简后得到关于θ的函数,易于求值域.

思路4在设出椭圆参数方程后,对得到的不等式进行化简,可得到关于sinθ的一次函数,利用一次函数的单调性,求出它在闭区间的值域,进一步得到关于a,b的不等式.

解法4(因式分解、函数思想)由解法2 可知(acosθ)2＋(bsinθ-b)2≤4b2对任意θ∈[0,2π)恒成立,整理得(b2-a2)sin2θ-2b2sinθ＋a2-3b2≤0,即[(b2-a2)sinθ＋a2-3b2](sinθ＋1)≤0.因为sinθ＋1≥0,所以(b2-a2)sinθ＋a2-3b2≤0对任意θ∈[0,2π)恒成立.令sinθ＝x(x∈[-1,1]),f(x)＝(b2-a2)x＋a2-3b2,则原问题转化为对任意x∈[-1,1],f(x)≤0恒成立.因为一次函数的一次项系数b2-a2＜0,所以一次函数在定义域[-1,1]上单调递减,故只需fmax(x)＝f(-1)＝2a2-4b2≤0即可,解得e∈,故选C.

通过因式分解将一个二次不等式化为一次不等式,从而将一个二次函数在闭区间的最值问题转化为一次函数在闭区间的最值问题,减少了计算量,优化了运算的路径,精简了运算的过程.

思路5这是一道选择题,能否运用解选择题的方法解决这道题呢? 例如,排除法、特殊值法等.如何抓住题目提供的条件进行排除,验证哪个特殊值最为有效?

解法5(排除法、特殊值法)如图3所示,当e→1时,椭圆不断变得“扁长”,总有一时刻|PB|＞2b,故排除选项A,B.对于C,D,可取特殊值e＝此时椭圆C＝1,点Pθ,bsinθ),又B(0,b),故|PB|2＝2b2cos2θ＋b2sin2θ-2b2sinθ＋b2＝4b2-b2(sinθ＋1)2,当sinθ＝-1,即点P与椭圆下顶点重合时,|PB|2取得最大值4b2,符合题意,进而排除D,故选C.

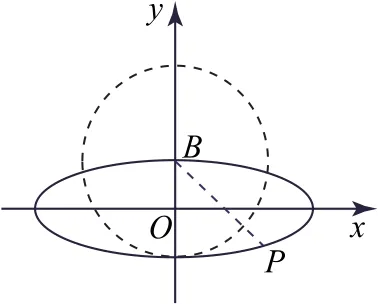
图3

观察上述5种解法,不难发现还是解法5最为高效、简捷.因此,做选择题可以思考用解选择题的特殊方法.当然,有时有些解选择题的特殊方法不能奏效,还需要进一步用直接法进行求解,要具体问题具体分析.

3 问题拓展

离心率是圆锥曲线中的一个重要元素,它的变化会直接导致曲线形状甚至类型发生变化.近年来,涉及离心率的问题频频出现在高考试题和各省市联考试题中,且题型不断翻新,显示出旺盛的生命力.解决有关离心率的问题,除了要求对离心率的概念、几何意义深刻领会外,还常常要用到其他有关知识,所以涉及离心率的问题不但具有很强的综合性,而且其解法极富灵活性.因此,对求离心率方法及策略进行研究具有重要的意义.

与离心率有关的题型有求离心率的值、求离心率的取值范围、探寻有关离心率的最值等.相对而言,求离心率取值范围的试题往往难度更大,解法更为灵活,涉及的知识面更广.

为了进一步掌握求离心率范围的方法,我们再看一个求椭圆离心率的取值范围的问题.

题目已知椭圆＝1(a＞b＞0)上一点A关于原点的对称点为B,F为其右焦点,若AF⊥BF,设∠ABF＝α,且α∈,则该椭圆的离心率e的取值范围是( ).

如图4 所示,设椭圆的左焦点为M,连接MA,MB,则|OA|＝|OB|,|OM|＝|OF|,又AF⊥BF,所以四边形AFBM为矩形.因为矩形的对角线相等且相互平分,所以|OA|＝|OM|,故∠AMF＝∠OAM＝∠ABF＝α.在Rt△AMF中,|AF|＝2csinα,|AM|＝2ccosα,根据椭圆的定义得2csinα＋2ccosα＝2a,故e＝.因为α∈所以e∈,故选D.

图4

本题是求离心率的取值范围问题,求解的通法是构造离心率关于一个变量的函数,将求离心率取值范围的问题转化为求函数值域的问题.很显然这里构造离心率e关于角α的函数关系较为合适.如何构造?难点就在这里.在圆锥曲线中出现焦半径可考虑定义法(定义法是解题的灵魂),而这里出现了焦半径|AF|,于是想到找到另一个焦点M,得到另一条焦半径|AM|,从而定义法应运而生,于是想到构造矩形得到等角,因此由椭圆定义就可得到等式2csinα＋2ccosα＝2a,进一步建立函数关系(运用辅助角公式).本题考查了学生的逻辑推理、直观想象、数学运算等核心素养,是一道好题.

4 小结

在高三的解析几何复习中,遇到稍微难一点的解析几何题目,我们应舍得花时间分析题目,寻找题目的各种解法,探讨各种解法的运算量、每种解法的运算路径如何设置、运算的节点如何把控、运算的过程如何监控等,阐明每一步运算的算理,注意每一步运算的细节和关键点,掌握常见的代数变换方法和必要的运算技巧,明确为什么这样算,这样算的优点和缺点分别是什么,运算的繁简度又如何,体会运算思路的形成过程,享受运算出结果带来的成就感,从而提升我们的数学运算素养.

对于一道题目不同的解法,应在思考中比较各个解法的优劣、运算的成本,各个解法的切入点、突破点、关键点、易错点,长此以往,我们的运算素养就会在比较、操作、优化、反思中得到提升.

在平时的解题训练中,要注重对题型的归纳和总结,在看到个性的同时找到共性,寻求规律性的东西,这样才能提高解题效率.例如,对于求离心率问题,通过上述例题不难看出,关键还是要掌握一些常见的思想方法(就是平时我们常说的通性通法)、记住一些常用结论、熟悉一些常用知识点,如方程思想、函数思想、消元法思想、等量代换、定义法、平面几何知识等.掌握这些方法及策略,求离心率问题便能迎刃而解.

(完)