多角度求解2020年新高考全国Ⅰ卷21题

陈熙春

(宁夏六盘山高级中学)

利用导数研究不等式恒成立问题或求解参数问题是导数的一个非常重要的应用,由于其形式多变、方法灵活,成为了近几年高考的热点与难点.本文以2020年新高考全国Ⅰ卷中的导数题第(2)问为例,探究了九种解法通过一题多思、一题多解,总结了利用导数解决不等式问题的常见方法,呈现了多种解题思路,展示了常见的转化技巧.多角度探究求解有利于学生系统掌握方法、启迪思维和全面提升解题能力.

1 真题在线

例(2020年新高考Ⅰ卷21)已知函数f(x)＝aex-1-lnx＋lna.

(1)当a＝e时,求曲线y＝f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

本题以基本初等函数为载体,考查利用导数研究不等式恒成立求参数的取值范围问题.解法的切入点具有多样性,是考查学生思维灵活性、拓展性的一道经典试题,具有极高的探究价值.这道题可以利用隐零点代换法进行求解,也可以对不等式进行放缩,将超越函数化为幂函数解决.

2 一题多解

(1)略.

(2)解法1常规解法(虚设零点——隐零点代换法)

对f(x)求导,得f′(x)＝(a＞0).设g(x)＝f′(x),则g′(x)＝aex-1＋＞0,所以g(x)在(0,＋∞)上单调递增,即f′(x)在(0,＋∞)上单调递增.

当a＝1时,f′(1)＝0,所以f(x)在(0,1)上单调递减,在(1,＋∞)上单调递增,所以fmin(x)＝f(1)＝1,即f(x)≥1成立.

即f(x)≥1恒成立.

当0＜a＜1 时,f(1)＝a＋lna＜a＜1,所以f(1)＜1,故f(x)≥1不是恒成立.

综上,实数a的取值范围是[1,＋∞).

解题关键是当a＞1时,找到f′(1)＜0,故f′(x)存在零点x0＞0,使得f′(x0)＝aex0-1-＝0,得到aex0-1＝,作整体代换,将超越式换成普通式,起到了“架桥铺路”的作用.研究函数的单调性、极值和最值时,都离不开导函数的零点这个基本问题.解题时经常会遇到导函数有零点但求解相对比较复杂或无法求解的情况,此时不必正面强求,只需设出零点,借助f′(x0)＝0进行整体代换和过渡,再结合其他条件就可以达到“柳暗花明又一村”的新境界.这种在形式上虚设,将超越不等式转化为普通代数式的方法称为“虚设零点——隐零点代换法”.

解法2常规解法(虚设零点＋构造函数)

又因为lna＝1-x0-lnx0,设h(x)＝1-xlnx,x∈(0,1),则h′(x)＝-1-＜0恒成立,所以h(x)在(0,1]上单调递减,所以h(x)≥h(1)＝0.当x→0时,h(x)→＋∞,所以lna≥0,即a∈[1,＋∞).

本题通过“隐零点代换”、构造函数解决问题,当然也可以用下面的方法解题.由f(x)≥1,得aex-1-lnx＋lna-1≥0,令g(x)＝aex-1-lnx＋lna-1,则gmin(x)≥0.后面和上述解法一样,通过求导利用隐零点代换法求解,两种方法殊途同归,体现了解法的灵活性.

f(x)＝aex-1-lnx＋lna＝elna＋x-1-lnx＋lna≥1等价于elna＋x-1＋lna-1≥lnx等价于

令g(x)＝ex＋x(x＞0),上述不等式等价于g(lna＋x-1)≥g(lnx).显然g(x)为增函数,故上式又等价于lna＋x-1≥lnx,即

令h(x)＝lnx-x＋1(x＞0),则h′(x)＝当x∈(0,1)时,h′(x)＞0,h(x)单调递增;当x∈(1,＋∞)时,h′(x)＜0,h(x)单调递减.

所以hmax(x)＝h(1)＝0,所以lna≥0,即a≥1,所以a的取值范围是[1,＋∞).

解题关键是在变形的基础上连续进行五次等价转化.第一次不等式等价转化为elna＋x-1＋lna＋x-1≥elnx＋lnx.第二次不等式等价转化为g(lna＋x-1)≥g(lnx).根据g(x)的单调性,第三次不等式等价转化为lna≥lnx-x＋1.令h(x)＝lnx-x＋1,第四次问题等价转化为求h(x)的最大值.第五次问题可转化为求解关于a的对数不等式lna≥0.解题关键是根据不等式的结构特点,构造恰当的辅助函数.

解法4放缩法

由题意可得x＞0,a＞0.因为f′(x)＝aex-1-,设h(x)＝f′(x),则h′(x)＝aex-1＋＞0,所以h(x)在(0,＋∞)上单调递增,即f′(x)在(0,＋∞)上单调递增.

吃茶品茗是自我反思，熏陶心志，修炼品格和参禅悟道的历程。《诗经·国风》中提及：“谁谓荼苦，其甘如荠。”饮茶是一个啜苦咽甘的轮回，茶水从淡到浓，从浓到淡，正如我们的人生。黄庭坚堪称饮茶修身的践行者，人生得意时，茶为诗人去掉心头的浮躁，忘却小我的个人得失，洞悉茶中真味和人生真谛，正确面对成功；人生低谷时，茶给诗人以温暖，能抑制生活中的清苦，物质上的简陋，使诗人平和心情，消除烦恼，让他鼓起奋起前程的勇气，随缘进取，因缘具足，成就圆满。

当0＜a＜1时,f′(1)＝a-1,且

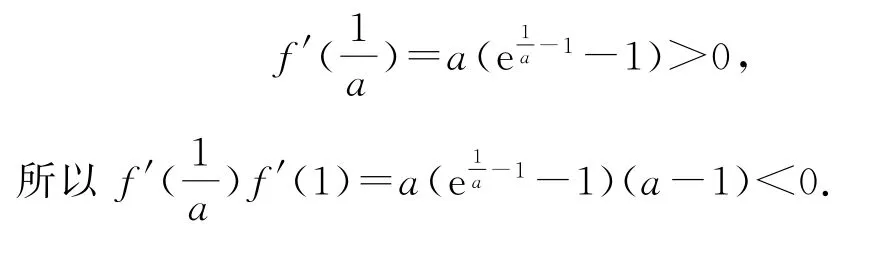
由零点存在定理可知存在x0∈(1,),使得f′(x0)＝0,当x∈(1,x0)时,f′(x0)＜0,函数f(x)单调递减,所以f(x)＜f(1)＝a＋lna＜a＜1,不满足题意.

当a≥1时,因为ex-1＞0,lna≥0,所以

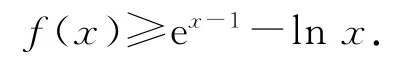
令g(x)＝ex-1-lnx,则g′(x)＝ex-1-,易知g′(x)在(0,＋∞)上单调递增,因为g′(1)＝0,所以当x∈(0,1)时,g′(x)＜0,函数g(x)单调递减;当x∈(1,＋∞)时,g′(x)＞0,函数g(x)单调递增,即g(x)≥g(1)＝1,所以f(x)≥1.

综上,a的取值范围是a∈[1,＋∞).

通过两次求导得到f′(x)在(0,＋∞)上单调递增,再对a进行分类讨论.当a≥1时,利用放缩法得到f(x)≥ex-1-lnx,再构造函数g(x)＝ex-1-lnx,用导数求出g(x)的最值,从而得到a的取值范围,充分体现了分类讨论和化归与转化的思想.

解法5指、对数不等式切线放缩法

因为aex-1-lnx＋lna≥1,所以

由指数不等式ex≥x＋1(证明略),得ex-1≥x,所以aex-1≥ax,当且仅当x＝1时取等号.又由对数不等式lnx＋1≤x,当且仅当x＝1时取等号(证明略),则式①可化为ax≥x-lna,即只需要证(a-1)x≥-lna(x＞0).

当a≥1 时,(a-1)x＞0,而-lna≤0,故(a-1)x≥-lna恒成立.

当0＜a＜1 时,(a-1)x＜0,而-lna＞0,故(a-1)x＜-lna不成立.

综上,a的取值范围是[1,＋∞).

由于题目中涉及超越不等式,难度较大,对不等式进行放缩,将超越函数化为幂函数.本题利用ex≥x＋1进行放缩.试题取材于人教A 版教材《选修2-2》中第32 页习题1.3B 组第1 题:对∀x∈R,证明:ex≥x＋1.题目中有ex,lnx,x,联想到重要的不等式ex≥x＋1,变形得ex-1≥x,lnx＋1≤x,当且仅当x＝1时取等号.熟练掌握不等式的推导和变形,回归教材,拓展例习题的条件和结论,实现知识迁移,找到试题的“源”与“流”.

由ex≥x＋1引出的常用的指数切线放缩公式有ex-1≥x(用x-1 替换x,切点的横坐标是x＝1),ex＋a≥x＋a＋1(用x＋a替换x,切点的横坐标是x＝-a),xex≥x＋lnx＋1(用x＋lnx替换x,切点的横坐标满足x＋lnx＝0).

同理,由对数切线不等式lnx≤x-1,切点为(1,0)引起的对数切线放缩公式有lnx≤(用替换x,切点的横坐标是x＝e),lnx≥1-(用替换x,切点的横坐标x＝1),或记为xlnx≥x-1,lnx≤x2-x(由lnx≤x-1及x-1≤x2-x,切点的横坐标是x＝1)或记为≤x-1.

放缩法是解决函数不等式问题的一把利器,关键是如何合理放缩.常见的一种放缩法是切线放缩法,曲线的切线为一次函数,除切点外,函数的图像在切线的上方或下方.利用这一特性,可以将超越函数放缩成一次函数,这种方法富有创意.

解法6“改头换面”切线放缩法

由f(x)≥1,即aex-1-lnx＋lna≥1,等价于

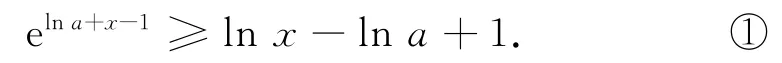
由ex≥x＋1放缩,得到

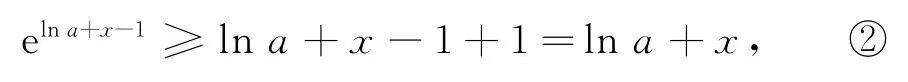
又由x≥1＋lnx(证明略),所以

结合式②得

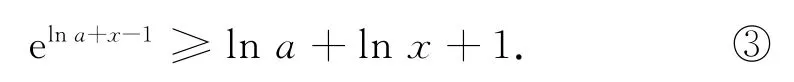
由①③得lna＋lnx＋1≥lnx-lna＋1,即2lna≥0,所以lna≥0,故a≥1.

利用ex≥x＋1,x≥1＋lnx将ex和lnx同时放缩成直线,这种方法称为“改头换面”.如ex-ln(x＋m)≥x＋1-(x＋m-1)＝2-m.

解法7构造“形似”函数法

所以当x∈(0,1)时,h′(x)＞0,h(x)单调递增;当x∈(1,＋∞)时,h′(x)＜0,h(x)单调递减,故hmax(x)＝h(1)＝1,故a≥1.

本题先将原不等式等价变形,使其左右两边具有相同“形似”结构,再构造“形似”辅助函数g(x)＝xex,将不等式转化为含待求参数的最值问题.本题在得到x≥ln时,即x≥1＋lnx-lna,也可以利用分离参数的方法,即lna≥1＋lnx-x,再利用构造函数的方法进行解决.令φ(x)＝lnx-x＋1,通过求导易得φmax(x)＝φ(1)＝0,所以lna≥0,即a≥1.也可以利用放缩法,由lnx＋1≤x,当且仅当x＝1时取等号,得到lnx-x＋1≤0,即φmax(x)＝φ(1)＝0,所以lna≥0,即a≥1.几种方法殊途同归体现了思维的灵活性.

解法8“一分为二”,构造两个函数

关于f(x)≥g(x)恒成立问题,通常方法是构造差函数h(x)＝f(x)-g(x),求出h(x)的最小值,证明其大于零,但很多问题最小值很难求出,属于“隐零点”问题,因此转化为两个函数的最值问题,即fmin(x)≥gmax(x),此类方法称为“一分为二”.根据不等式①的特殊性,“一分为二”分别构造函数h(x),g(x),因为两个函数的凸性相反,转化为两个熟悉的函数图像,再构建不等式求解.研究函数h(x)和g(x)的最值,求出a的范围.这种方法思维层次高,很有新意,让人赏心悦目.

解法9必要性探路法

因为f(x)＝aex-1-lnx＋lna,所以由必要性得f(1)＝a＋lna≥1.令g(x)＝x＋lnx(x＞0),易知函数g(x)在(0,＋∞)上单调递增.因为g(a)＝a＋lna≥g(1)＝1,所以a≥1.下证充分性.

当a≥1时,有

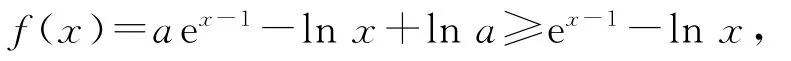
所以只需证ex-1-lnx≥1.令h(x)＝ex-1-lnx,则h′(x)＝ex-1-,易知h′(x)为增函数,且h′(1)＝0.故当x∈(0,1)时,h′(x)＜0,h(x)单调递减;当x∈(1,＋∞)时,h′(x)＞0,h(x)单调递增.所以h(x)≥h(1)＝1,此时f(x)≥h(x)≥1.

综上,a的取值范围是[1,＋∞).

采用必要性探路法证明,先得到a的取值范围,之后再证明充分性,大大降低了解题的难度.

3 小结

这道经典的高考题,体现了低起点、多层次的特点,再次明确释放出要重视课本的信号.树高千尺也忘不了根,课本就是高考复习的“根”.知识源于课本,思想方法源于课本,高考试题源于课本.因此,复习中需要认真研究课本知识,高考总复习的秘诀就是抓落实,而用好教材就是最好的落实.

高考试题具有深刻的背景和内涵,具有极高的研究价值,通过研究高考试题,可以更好地揭示解题规律,掌握高考试题的特点,把握高考复习方向.

在高考复习过程中,教师要带领学生研究高考试题,充分挖掘其承载的思想方法.通过一题多思、一题多解,在展示各种解法的形成过程中深入研究,从而比较各种解法的思维量和运算量,更好地揭示解题规律,在分析和比较中培养学生的发散思维能力和探究能力.本文中的九种解题方法各有千秋,从多方位、多角度、多层次看问题,展示了各种解法的形成过程,凸显了思维的灵活性.

(完)