针对机动目标的改进型交互多模型跟踪算法研究*

杨冬英，贺江鹏

(1.山西大学商务学院,山西 太原 030031；2.山西北方机械制造有限责任公司，山西 太原 030009 )

1 引言

早在20世纪中叶，针对机动目标定位与跟踪的思想就引起了各国的重视[1]。机动目标的跟踪最早主要应用于军事领域，常使用声纳、雷达等对飞机、舰船和导弹等实施定位与跟踪[2]。由于其复杂程度高和随机性大，机动目标的跟踪也成为了目前精确打击与反打击的研究热点。

传统跟踪方法主要从2个方面考虑：(1)提高目标模型的鲁棒性；(2)提高目标滤波精度。目标模型的测试精度取决于其描述机制，而跟踪算法的优劣主要体现在其算法的实时性上。对滤波算法的改进主要通过优化求解方式实现，调节目标跟踪过程中不同的参数可以实现突出目标特征的效果，从而提高滤波精度。目前主流的机动目标跟踪算法是基于交互多模型IMM(Interacting Multiple Model)[3,4]技术实现的。常见的滤波器有卡尔曼滤波KF(Kalman Filtering)[5]、高斯滤波(Gaussian Filtering)[6]和一些结合型滤波方法，如扩展型卡尔曼滤波EKF(Extended-KF)[7]、不敏型卡尔曼滤波(Unscented-KF)[8]等。

Ehrman等[9]研究了近距离目标的跟踪识别，提出了针对目标散射面积变化的目标跟踪算法。Mertens等[10]利用施威林模型对目标散射面分布进行特征分析，从而提升了目标识别精度，并在近距离目标跟踪实验中得到了验证。Zhou等[11]利用多普勒效应求解目标径向速度，将静态融合与卡尔曼滤波器相结合，提升了跟踪性能。Brekke等[12,13]设计了一种基于目标幅度信息的快速信息关联算法，使跟踪过程不易丢失目标，鲁棒性较好。Bi等[14]利用奇异值分解法对高分辨率距离像进行三维重建，使测试数据可用于目标识别。靳标等[15]利用多特征滤波的方式实现了对高分辨率距离像中多目标的同时求解，提高了跟踪精度。高颖等[16]将EKF与IMM相结合，提出了一种机动目标的IMM扩展卡尔曼滤波时间配准算法，对低维机动目标具有较好的跟踪效果。

综上所述，本文提出了一种改进型交互多模型跟踪算法，利用对状态估计中协方差的参数调节，实现与目标特征的数据关联，从而提高目标识别精度。

2 数学模型的构建

当机动目标在图像采集区域运动时，可以将其在图像中投影获得的偏转角作为整个跟踪轨迹的关联变量，该偏转角如图1所示。

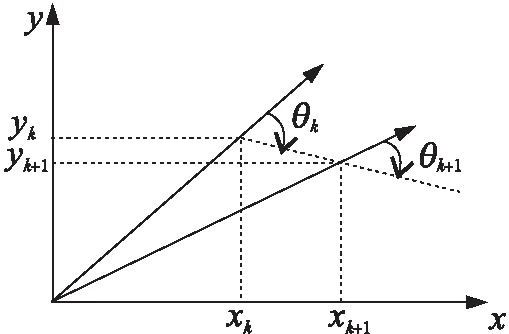
Figure 1 Deflection angles of associated variables

由图1的角度关系可推导得到目标在图像中的夹角，如式(1)所示:

(1)

其中，θk表示k时刻的偏转角度，如图1中所示；(vx,vy)表示目标在x轴向和y轴向上的速度。在此基础上，目标的状态可以由状态方程表示，如式(2)所示:

(2)

其中，Xk表示k时刻目标的状态;T表示转置；(xk,yk,zk) 为k时刻3个轴向上的位置量；(vxk,vyk,vzk) 为k时刻在3个轴向上的速度；Fk|k-1为目标转移矩阵；wk-1为白噪声。

3 改进型交互多模型跟踪算法设计

改进型交互多模型跟踪算法是在IMM的基础上实现的，为了解决非线性滤波问题，本文引入了与目标特征具有关联性的协方差参数调节项，从而使非线性滤波过程具有目标特征参考因素，进而提高目标识别精度。

3.1 改进型IMM模型

图2是改进型IMM模型结构图。由图2可知，首先是数据输入层的信息交互，在第k-1时刻，交互产生的第n个滤波器的输入数据可表示为式(3):

(3)

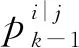
(4)

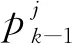
在k-1时刻滤波输入的基础上，可得到k时刻的滤波输出，其概率更新如式(5)所示:

(5)

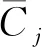
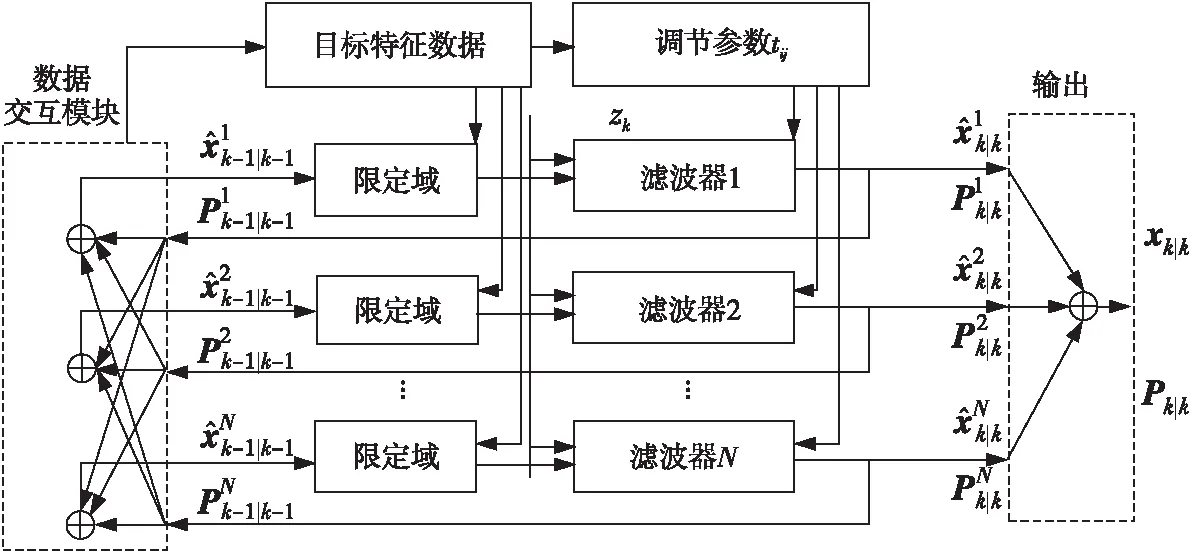
Figure 2 Improved IMM model

3.2 目标特征关联参量滤波

传统方法是在IMM模型的基础上将对应类型的滤波器模块加载到图2中滤波器N的位置，从而实现对目标的滤波识别。本文算法的核心思想是在输入端将目标特征信息作为边界条件与输入数据进行相关运算，然后再通过在滤波器中设置调节参数的方式来实现对目标特征的精确筛选，进而提高识别精度。引入具有目标特征关联性的参量步骤如下所示：

步骤1测量数据与目标特征数据交互计算，则在k-1时刻时，任意2个参量之间的交互概率可表示为式(6):

(6)

其中，tij为目标特征数据组调节参数，其它各参数定义与前文一致。

由此在n个运动模型中，可得引入调节参数的状态估计和交互协方差如式(7)所示:

(7)

步骤2对测量数据和状态数据进行更新，将引入目标特征的数据作为滤波器输入数据，即在zk位置将原数据进行特征化更新，则交互协方差如式(8)所示:

(8)

由式(8)可知，原有测量数据与特征数据匹配后得到的新数据是计算交互协方差的依据。与之对应的模型i条件下的状态增益矩阵和协方差矩阵可表示为式(9):

(9)

步骤3将在模型i条件下的状态估计与协方差计算遍历到所有测量数据中，得到最终的状态估计与估计协方差，如式(10)所示:

(10)

步骤4以式(10)的最终结果作为输出，完成测量数据目标识别的分类计算。由于在输入数据端测量数据是预先与目标特征模型进行匹配的，所以当进入滤波算法时，只要对特定目标的特征信息进行迭代对比，目标的可识别性就会大大增加，从而显著提升系统识别精度。

改进算法将具有目标特征的限定域以滤波函数的方式引入到数据计算中，可以等效成在原有数据运算过程中增加了一个与限定域求交集的过程，这个交集运算能大幅降低原有数据的维度，故对总体数据运算量的降低具有很好的作用。传统算法与改进算法的运算量之比为限定域系数平均值的反比，可知改进算法的运算量被大幅减小，加快了算法运行速度。

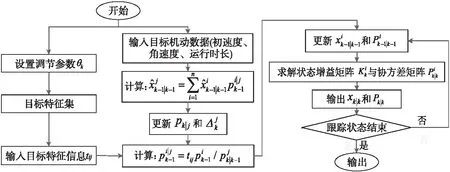
Figure 3 Flow chart of interactive multi-model tracking algorithm

3.3 算法实现流程

根据模型结构和可调参量对模型改进的关系可知，本文算法将目标特征信息作为先验条件对初始数据进行匹配，实现预处理数据选择的指向性；然后再在滤波算法中以目标特征作为边界约束条件提高目标识别精度，算法流程如图3所示。因为在实际环境中无法预知的环境噪声是使测试系统测试精度突然出现错误的重要因素，故分析随机噪声背景比某类型系统噪声更有意义。为了更好地模拟目标跟踪过程，在仿真分析过程中添加了随机噪声。

4 实验与结果分析

为了验证本文算法的可行性，采用对相同数据组进行识别分析的方法，分别用本文算法和传统IMM算法对仿真数据进行目标识别与跟踪。

4.1 仿真过程参数设置

机动目标模拟仿真过程为先完成一段均速飞行，时速150 m/s，运动40 s(匀速模式，CV，Constant Velocity)；再以角速度0.03 rad/s的速度完成转弯，运动20 s(匀速转弯模式，CT，Constant Turn)；最后以10 m/s2的加速度，运动40 s(匀加速模式，CA，Constant Accelerate)。实验对整个运动轨迹过程进行跟踪计算,并对比2种算法的跟踪精度。仿真过程中，为了同时考察运动实时性对跟踪效果的影响，给出了不同偏转角条件下的算法求解差异。

4.2 评价标准

算法的最终目的是完成目标的定位与跟踪，所以目标的位置与速度求解精度是重要的评价标准。设采样时刻k时，测量目标的位置是(xk,yk)，x轴和y轴的表达方式相同。则其位置的均方根误差(Error|xk)和速度的均方根误差(Error|vk)可表示为式(11):

(11)

其中，N表示算法迭代总次数，i表示第i次实验，x表示位置，v表示速度。由此完成对不同算法跟踪结果的评价。

4.3 测试结果分析

分别采用传统IMM算法和本文算法对相同的模拟航迹数据进行跟踪计算，同时,本文算法分别采用偏转角计算精度为1°,2°和4°的不同阈值档位。仿真结果如图4所示。

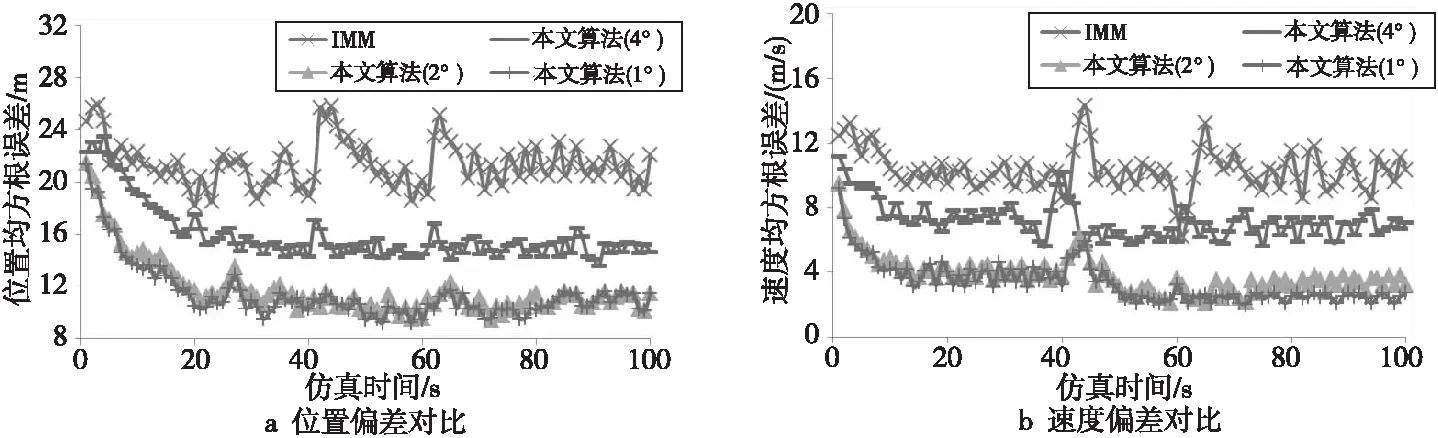
Figure 4 Comparison of tracking error results under different parameter conditions

在整个机动目标跟踪过程中，位置均方根误差变化由图4a所示，传统IMM算法的位置均方根误差均值为21.39 m，而在本文算法中偏转角分别为4°,2°和1°时，均方根误差均值分别为15.91 m,11.79 m和11.39 m。仿真结果显示,不同的偏转角对算法计算获得的精度是有影响的，当偏转角为1°和2°时，精度基本一致，但当偏转角设置为4°时，精度明显下降，故在实际测试应用中要求采样速度满足偏转角变化小于2°，以保证计算精度。由此可知采用本文算法的位置跟踪精度优于采用传统IMM算法的，同时，随着本文算法中调节参数偏转角的引入，算法精度可以进一步提高，当其小于2°时，均值优于12 m。同时，可以看出偏转角为1°时，误差的降低幅度相比于2°时下降不明显，但其运算量却要增加一倍，故在本文优化过程中，为了保证算法的实时性，最终选择2°作为算法偏转角参数的最优值。在40 s与60 s处出现了2处误差峰值，分析起源在于该时刻目标机动的类型突然转变，对位置和速度的预估均有一定影响，但随着时间的推移，该误差会逐渐恢复到正常水平。此误差波动现象在传统算法中比较明显，而采用偏转角参数校正的本文算法中，该现象会随着偏转角设置精度的提高而受到抑制。由此可见，通过调节参数设置的方法对传统算法进行改进确实可以实现位置及速度跟踪精度的提升。

5 结束语

本文提出了一种改进型交互多模型跟踪算法，通过引入包含目标特征信息的调节参数偏转角作为算法反馈调节量，完成对初始数据的匹配，并以对应的匹配滤波器实现有效数据的保留。该算法相比传统IMM算法而言，位置和速度的跟踪精度均有所提高，并对运动状态改变导致的误差激增有较好的抑制效果。总之，该算法在提高机动目标跟踪精度方面具有一定的应用价值。