面向硬件实现的64进制LDPC译码算法研究与性能评估
2022-04-21树玉泉章林锋胡志蕊刘轶龙贡冀鑫
树玉泉,章林锋,胡志蕊,刘轶龙,贡冀鑫
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.中国人民解放军32021部队,北京 100094)
0 引言
北斗三号全球卫星导航系统于2020年7月正式开通投入运行,向全球用户提供位置服务、应急搜救和精密单点定位等多种特色服务。根据北斗系统空间信号接口控制文件B1C,B2b和B2a,北斗系统下行信号电文使用了(200,100)(162,81)(96,48)(88,44)四种长度的六十四进制低密度奇偶校验码(Low Density Parity Check,LDPC)作为主要信道编码形式。与二进制LDPC相比,多进制LDPC具有更低的误码平层和更高的增益[1-2],但是由于其译码复杂度较高,对硬件资源较为紧张的接收机设计带来了挑战[3]。
Gallager[4]于1963年提出了二进制LDPC,并得到了广泛应用[5-7]。1998年,Davey和Mackay[8]研究了基于有限域的多进制LDPC,并给出了多进制LDPC的和积译码算法(Q-ary Sum-Product Algorithm,QSPA),多进制LDPC的性能要优于二进制LDPC码,但这是以更大的编译码复杂度换取的。对于定义在GF(q)域的LDPC码,其中q=2p,标准的和积译码算法复杂度会随着p的增加而迅速增加。而另一方面,随着进制数的提升,其抗突发错误能力越强。因此,对于多进制LDPC的研究集中在如何降低译码算法复杂度。
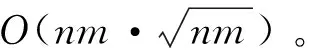
本文面向接收机硬件实现,将基于FB算法的BC方案应用到校验节点更新中,并通过优化变量存储机制,减少不必要过程变量的存储,进一步优化了资源消耗。在此基础上,基于Xilinx的XC7K325T FPGA开发了(200,100)(162,81)(96,48)(88,44)四合一译码模块,开展了性能验证和分析,在性能、译码时延等方面找到了适应北斗三号全球卫星导航系统接收机的参数配置方案。
1 传统译码算法
T-EMS算法虽然译码速率快,但需要存储较多路径,不利于资源优化,且该算法性能相比于EMS算法略有降低。由于北斗三号全球卫星导航系统下行电文速率较低,对于地面接收来说译码速率不是第一诉求。而且一般的导航接收机硬件资源有限,极大限度地压缩译码模块的资源占用是更有意义的。因此,本文选择EMS系列算法进行研究,分析其复杂度的核心因素,并面向硬件实现,从资源优化、流水线处理等方面进行了针对性的设计。
1.1 EMS算法
对于GF(q),q=2p域上的多进制LDPC,假设其码长为n,信息长度为m,校验矩阵为H,行重为dc,EMS译码算法描述如下:
① 初始化数据
将接收到的数据进行处理,获得每个符号位取值的概率信息:
j=0,1,…,n-1,ak=0,1,…,q-1,
(1)
式中,Lj(ak)表示第j个符号位取值为ak的概率信息;zj为相对于yj而言通过信道信息估算出来的最有可能的符号,因此,有Lj(ak)≥0,且Lj(ak)的取值越小代表该符号位取值为ak的概率越大。
利用初始信息Lj(ak)建立变量节点更新矩阵:
Lqij(0)(ak)=Lj(ak)
i,j∈{N(i),C(j)}={Hi,j≠0},
(2)
式中,Lqij(0)(ak)为变量节点的初始化矩阵;N(i)为校验矩阵H的行重集合;C(j)为H矩阵的列重集合。
② 校验节点的运算(水平运算)
第l次迭代,校验节点更新如下:
(3)
Ψ(i|aj=ak)={(aj′)j′∈N(i){j}|Hijak+
(4)
式中,Lr(l)ij为第l次迭代时的校验节点矩阵;Ψ(i|aj=ak)为变量节点参与更新运算的集合。
③ 变量节点的运算(垂直运算)
第l次迭代变量节点更新如下:
(5)
式中,Lqij(l)为第l次迭代时的变量节点矩阵。
④ 判决输出
(6)
yj=argmin(Lqj(l)(ak)),
(7)
式中,yj为最终判决输出的译码结果。
1.2 复杂度分析
可以看出,校验节点的更新是制约多进制LDPC译码复杂度的核心因素。式(4)是校验节点更新时用到的集合,该集合的大小随q和dc的变大而急剧增加。对于北斗三号全球卫星导航系统使用的六十四进制LDPC而言,q=64,dc=4,每次迭代更新1个有效位置需要计算643次,共有m×dc个有效位置。如此高的运算量对于硬件实现来说是不可承受的。
为了降低译码算法的运算量,将从算法层面的资源优化方案和实现层面的流水线处理方案两方面入手,降低硬件实现的复杂度。
2 面向硬件实现的译码方案
2.1 资源优化
资源优化将从两方面入手。引入置信长度的概念主要为降低运算量,变量存储机制主要优化运算过程中变量所需的存储资源。
2.1.1 置信长度
因为最终判决是选择每个符号位取值最小的概率信息对应的域元素,在进行校验节点更新运算时,可以将取值较大的概率信息舍去,每个符号位只传递概率信息值最小的nm个变量及其对应的域元素。nm即置信长度。可将式(4)改写为:
sort(Lqij′(l-1))
aj′∈conf(Lqij′(l-1),nm)
(8)
首先对Lqij′(l-1)进行从小到大排序,域元素也对应调整,conf(Lqij′(l-1),nm)为前nm个概率信息对应的域元素的集合。可以看出,通过运算复杂度与nm呈正相关,但是nm取值过小会影响译码增益。一般来说,nm≥0.5×q时,将不会对译码增益产生明显影响。下面将对nm的取值做进一步的仿真分析。
2.1.2 变量存储机制
传统的EMS算法中,核心的处理为校验节点Lr(l)ij(ak)的更新运算和变量节点Lq(l)ij(ak)的更新运算,需要存储Lr(l)ij(ak)和Lq(l)ij(ak)。2个变量均为三维矩阵,大小为m×dc×q。由式(5)和式(6)可以看出,最终译码结果的判决只和Lr(l)ij(ak)有关,Lq(l)ij(ak)仅作为中间变量参与存储。因此,可以考虑将第2步校验节点的运算和第3步变量节点的运算进行整合。
第1步:初始化数据
Lrij(0)(ak)=0,
(9)
Lqj(0)(ak)=Lj(ak)。
(10)
第2步:迭代更新
第l次迭代:
For:i=1:m
Lqij(l)(ak)=Lqj(l-1)(ak)-Lrij(l-1)(ak),
(11)
(12)
(13)
End
第3步:判决输出
yj=argmin(Lqj(l)(ak))。
(14)
可以看出,整个译码过程精简为3步,整合后的运算过程将变量节点更新和校验节点更新耦合在一起,使得整个译码过程更为紧凑。Lqij(l)(ak)的维度由m×dc×q减小为dc×q,且仅需临时存储。通过上述设计,可以进一步节省存储资源并降低时延。
2.2 FB-BC流水线处理
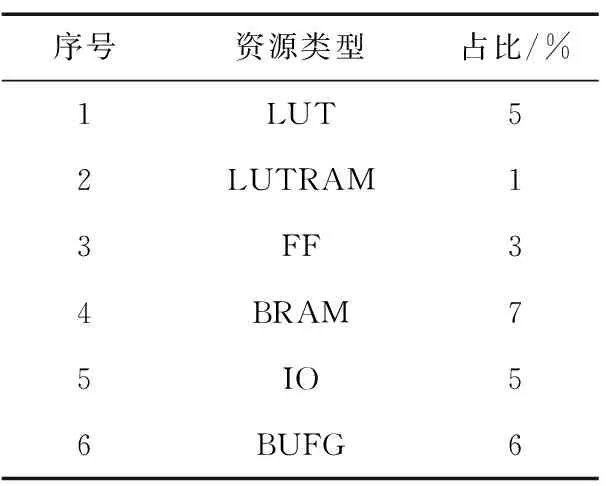
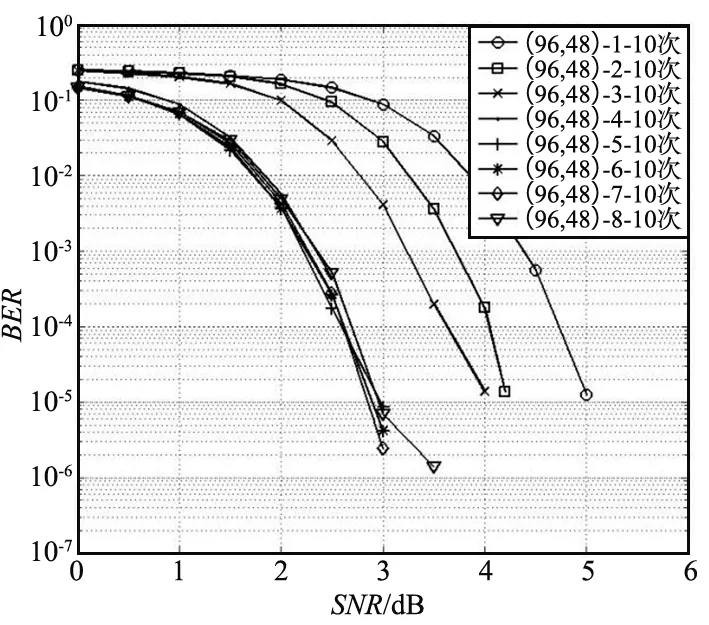
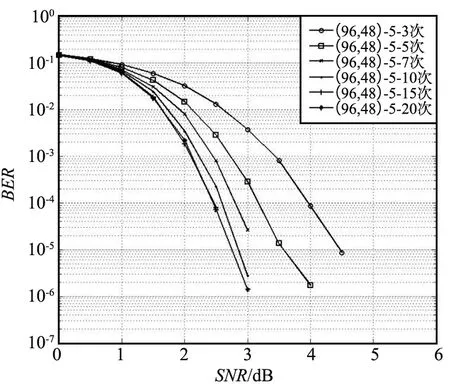
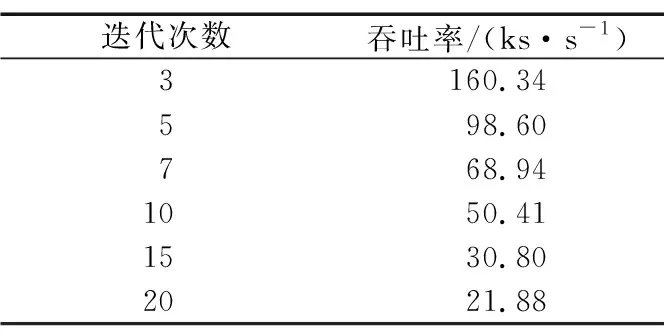
将校验节点的运算拆解成两两运算。以校验节点第m行为例,行度为dc,ni表示第m行第i个有效位置,0≤i 前向计算: (15) 后向计算: (16) 校验节点信息更新: (17) 可以看出,上述操作中均有一步相同的运算,命名为基本运算(2个输入、1个输出)。建立基本运算模块,校验节点更新重复调用该模块,可流水线操作并减小资源占用。 关于基本运算模块有如下简单算法: 该模块设置有2个输入和1个输出,输入为V和I以及对应的索引Vq和Iq,输出为U和Uq。V和I均是按从小到大排序好的序列。建立一个虚拟矩阵M(该矩阵在实际实现时无需存储,仅仅是便于理解)和排序器S,S的作用是找最小值。 M中的元素为V和I的对应操作: M(i,j)=max(V(i),I(j)),i,j∈[0,nm]。 (18) 步骤如下: ① 将M的第1列及其对应的域元素送入排序器S; ② S找出最小值,并将结果输出至U,如果该结果对应的域元素已经存在于U中,则不做操作;否则将结果放入U,对应域元素放入Uq; ③ 将该结果在虚拟矩阵中的右邻居放入S; ④ 返回步骤②。 基于第2章的资源优化方案和FB-BC流水线处理方案,开发了四合一仿真译码模块,并对译码模块的量化位数、迭代次数和置信长度等参数配置进行仿真分析,得到了推荐的参数配置。最终对北斗三号全球卫星导航系统应用的4种六十四进制LDPC进行了综合性能分析。 为了验证算法的可实现性,对北斗三号全球卫星导航系统六十四进制LDPC性能在量化位数、迭代次数和置信长度等方面进行了较为全面的仿真分析,基于Xilinx的XC7K325T FPGA开发了(200,100)(162,81)(96,48)(88,44)四合一译码模块,译码模块的资源占用如表1所示。 表1 四合一译码模块FPGA资源占用 由表1可以看出,该译码模块的硬件资源占用XC7K325T芯片资源较少,可满足工程的使用需求。 此外,还开发了测试评估软件,与四合一译码模块构成了半实物仿真系统。测试评估软件产生电文并进行编码、加噪声和量化处理,并传输至四合一译码模块,译码模块完成译码后,将译码后的电文传输至上位机软件,上位机软件完成译码时延和误码率的统计,并借助Matlab的绘图功能绘制误码率曲线。该译码模块的迭代次数、量化位数和置信长度等均可配置。 不同的译码模块参数配置会对资源占用、译码时延和译码增益等产生影响,对于接收机设计,应根据需求选取合适的参数配置,不应一味地求全,进而造成不必要的资源浪费。本节主要基于(96,48)六十四进制LDPC对译码模块的量化位数、迭代次数和置信长度等参数配置进行仿真分析,并得到推荐的参数配置。 由于3个参数相互独立,因此仿真过程采用控制变量法,即在进行某一项参数仿真时固定另2个仿真参数。基本仿真参数设置如下: ① 噪声添加方式:加性高斯白噪声(Additive White Gaussian Noise,AWGN)。 ② 调制方式:二进制相移键控(Binary Phase Shift Keying,BPSK)调制。 ③ 电文:随机产生0,1。 ④ 硬件模块运行的时钟为60 MHz。 ⑤ 在误码率为10-5时计算译码增益。 其中,运行时钟是影响硬件模块运行速率的主要因素之一,本文对于译码模块吞吐率的结论是在60 MHz时钟频率下得到的。 3.2.1 量化位数仿真 量化位数仿真中,迭代次数设置为10次,置信长度nm为32。量化位数遍历了1~8,并绘制了误码率曲线,如图1所示。 图1 量化位数仿真 由仿真结果可以看出,随着量化位数在1~4增加,译码增益提升明显,4 bit量化比1 bit量化译码增益增加了2 dB。但是继续增加量化位数译码增益几乎不再发生变化。因此,可以看出,在4 bit及以上量化时,由量化引起的信道信息已不明显。 量化位数是直接影响译码模块资源消耗的因素之一,为了避免不必要的资源开销,可选择4~5 bit量化。 3.2.2 迭代次数仿真 迭代次数仿真中,量化位数设置为5 bit,置信长度nm为32。分别对3,5,7,10,15和20次迭代进行了仿真,并绘制了误码率曲线,如图2所示。 图2 迭代次数仿真 由仿真结果可以看出,迭代次数3,5,7,10之间译码增益差异明显,10次迭代比3次迭代增加了1.5 dB。但10次迭代与15次迭代之间仅相差0.1 dB,15次迭代和20次迭代几乎重合,增益不再增加。10次迭代时获得6.7 dB的增益,即可充分发挥多进制LDPC的优势。 不同迭代次数的吞吐率对比结果如表2所示。 表2 不同迭代次数的吞吐率对比 由表2可以看出,迭代次数是直接影响译码模块吞吐率的因素,随着迭代次数增加,吞吐率呈等比例下降趋势。北斗下行电文速率最快不超过1 ks/s,相比之下,在10次迭代时可获得50.41 ks/s的吞吐率,可满足接收机的使用需求。考虑到迭代次数的变化并不涉及译码模块内部的调整,可灵活进行配置,因此建议迭代次数可设置为5次和10次两档,根据实际接收信号的载噪比进行动态调整。 3.2.3 置信长度仿真 置信长度仿真中,量化位数设置为5 bit,迭代次数设置为10次,置信长度nm分别取值为8,16,32和64,并绘制了误码率曲线,如图3所示。 图3 置信长度仿真 由仿真结果可以看出,nm=16时译码增益比nm=8时增加约0.6 dB,nm=32时译码增益比nm=16时增加约0.1 dB,nm取值为32,64时增益变化不再明显。 置信长度可直接影响译码时延,建议选择32。 3.2.4 小结 从量化位数、迭代次数和置信长度仿真可以看出,为了保障接收机获得高可靠的电文信息,可选择如下参数资源配置: ① 量化位数5,迭代次数5,置信长度32。 ② 量化位数5,迭代次数10,置信长度32。 配置①可用于接收载噪比较高的通道,配置②可用于接收载噪比较低的通道。 选择上节推荐的2种参数组合对(200,100)(162,81)(96,48)(88,44)四种长度的六十四进制LDPC性能进行综合仿真分析,并与同等长度的二进制LDPC进行了对比分析。二进制LDPC使用NMSA算法,5 bit量化,10次迭代,如图4所示。 图4 性能综合分析 根据仿真图,可以得到北斗三号全球卫星导航系统使用的4种六十四进制LDPC的增益,以及和二进制LDPC的增益对比,如表3所示。 表3 译码增益对比 由表3可以看出,基于本文的译码硬件实现方案,同等长度下北斗三号全球卫星导航系统六十四进制LDPC比二进制LDPC约有0.2~0.3 dB的性能增益。同等长度下,10次迭代比5次迭代性能可提升0.7~0.8 dB。 对传统的EMS算法进行了描述和复杂度分析,得出了制约北斗三号全球卫星导航系统六十四进制LDPC译码实现的主要因素。从译码过程和资源存储两方面进行了针对性设计,提出了校验节点和变量节点深度耦合的实现方案,优化了译码过程和存储资源占用。并引入FB-BC流水线处理机制,最终形成了面向硬件实现的译码方案。基于该方案开发了四合一译码模块,并开展了参数仿真分析和综合仿真分析。参数仿真分析表明,量化位数5、迭代次数5或10、置信长度32时是资源、时延和增益三方面综合最优的搭配,其中10次迭代即可基本发挥出多进制LDPC的译码增益优势。综合仿真分析表明,基于本文提出的方案,可获得6.7~7.1 dB的译码增益,并比同等长度的二进制LDPC获得约0.2~0.3 dB的性能增益。本文的研究成果可为北斗三号全球卫星导航系统接收机的设计提供参考。3 硬件实现及仿真分析
3.1 四合一译码模块
3.2 参数仿真分析
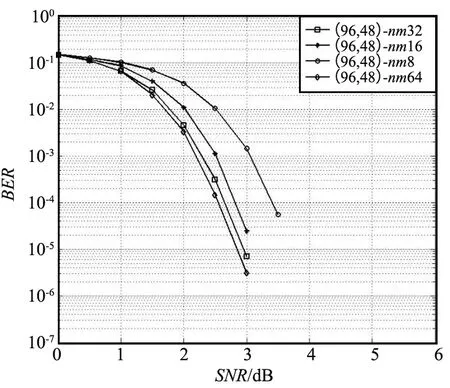
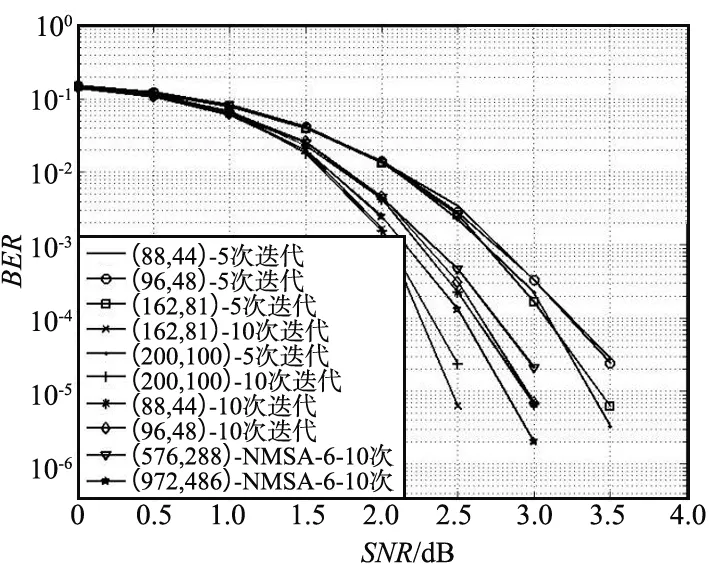
3.3 综合仿真分析

4 结束语
