基于Nyström的一种新颖的DOA估计算法

马 腾，杜 江*，乔理扬，黄天赐

(1.成都信息工程大学 通信工程学院，四川 成都 610225;2.气象信息与信号处理四川省高校重点实验室，四川 成都 610225;3.四川大学 电气工程学院，四川 成都 610065)

0 引言

波达方向(Direction of Arrival,DOA)估计在雷达及通信等领域有着广泛的应用且是阵列信号处理的重要研究分支及组成部分[1-2]。经典的基于子空间的多重信号分类算法(MUSIC)[3]开创了超分辨空间谱参数估计的先河，该算法测向精度高且理论推导不复杂，但运算量较大，在有些场合不太适合信号的实时处理。其运算量主要集中在阵列输出的协方差矩阵的计算、协方差特征分解得到信号和噪声子空间及谱峰搜索，且谱峰搜索随着搜索精度的提升，运算量急剧增加。为了避免或减少谱峰搜索从而降低运算量，有学者提出了经典的求根MUSIC(MUSIC-root)[3]、旋转不变子空间算法(ESPRIT)[4]，以及闫锋刚等[5-8]提出的一整套压缩谱理论，但仍需计算阵列输出的协方差及对其特征分解。此外，为了减少整体算法中复矩阵间的运算量，酉变换被引入并衍生了一系列算法[9-10]，其使复矩阵间运算变为实矩阵间运算，大大降低了计算复杂度。

为了避免直接对所有阵列输出计算协方差及对其特征分解得到信号或噪声子空间，降低运算复杂度，一些快速参数估计算法被提出。如传播算子算法(PM)[4]及其衍生算法[11],通过线性运算代替协方差矩阵的特征分解，间接得出信号及噪声子空间。应用多级维纳滤波(MSWF)[11-12]技术进行快速DOA估计,通过多级维纳滤波前向递推间接获得信号子空间和噪声子空间，避免了直接对阵列输出的协方差矩阵的特征分解。但基于多级维纳滤波技术的方法需要知道原始信号作为参考，实际应用性不强。近些年，一种Nyström方法被用于DOA估计中[13-15]。其最初应用于机器学习中的核机器学习领域[16]。该方法在离散空间中也可以用来逼近对应数据的特征矢量，即Nyström方法的矩阵表示形式。目前Nyström方法是一种较流行的“低秩矩阵逼近算法”之一。在DOA估计中应用该方法，无需计算所有阵列输出数据的协方差矩阵及对其直接进行特征值分解得到信号子空间，而是通过阵列输出的部分块矩阵直接得到一种等效的逼近信号子空间，极大地减少了计算复杂度。

本文将结合Nyström方法提出一种新颖的DOA估计算法，在得到逼近的信号子空间后，无需像大多数现有的DOA估计算法通过矩阵间的运算或谱峰搜索得到DOA估计，而是通过逼近的信号子空间构建低阶的特征多项式方程，此多项式方程的阶数仅与信号源数目相同(信号源数通常远少于阵列阵元数)，不同于现有的DOA估计求根类算法所建立的多项式，其阶数大约为2倍的阵列阵元数[11，17-18]，对此低阶多项式求根相比高阶多项式方程求根得到DOA估计更加提升了计算效率。通过理论分析及仿真实验对比其他算法说明了所提算法的性能。

1 阵列信号数学模型

天线阵列模型如图1所示，假设有K个远场非相干窄带信号入射到共有M个天线阵元的一均匀线性阵列(ULA)，各阵元之间间距d为传播波长λ的一半。

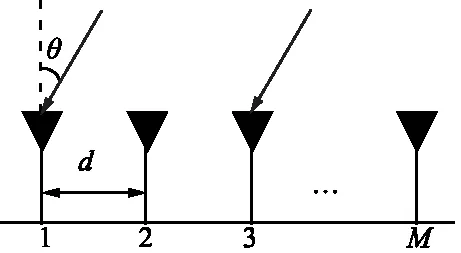
图1 天线阵列模型

阵列在t时刻对应第m个阵元的输出可表示为：

(1)

式中，sk(t)为第k个入射信号；nm(t)为第m个阵元受到的高斯白噪声干扰；θk为第k个信号的DOA。定义θk方向向量为：

(2)

阵列流型矩阵A定义为A=[a(θ1),a(θ2),…,a(θk)]，所有M个阵元的输出为x(t)=[x1(t),x2(t),…,xM(t)]T。当快拍数为L时，阵列输出可写成如下形式：

X(t)=[x(t1),x(t2),…,x(tL)]=AS(t)+N(t)，

(3)

式中，X(t)为M×L维阵列输出数据；S(t)=[s(t1),s(t2),…,s(tL)]为K×L维入射到阵列的信号；N(t)=[n(t1),n(t2),…,n(tL)]为M×L维加性高斯白噪声。则可定义阵列输出的协方差矩阵为：

R=E[X(t)XH(t)]=ARSAH+σ2IM，

(4)

式中，RS=E[S(t)SH(t)]为信号源S(t)的信号协方差矩阵；IM为M×M维单位矩阵。通常在实际应用中，式(4)的协方差矩阵R通过下式估计得到：

(5)

在得到阵列输出的协方差矩阵R后，其特征分解可表示为：

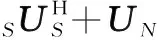
(6)

式中，US为信号子空间，由与信号源数目相同的K个较大特征值所对应的特征向量构成；UN为其余的M-K个特征向量组成的噪声子空间。得到信号及噪声子空间后，可通过MUSIC,ESPRIT等算法及其衍生算法进行DOA估计。下一节将对提出的新颖的DOA估计算法进行阐述。

本文中右上标“*”表示复共轭，“T”表示转置，“H”表示共轭转置，“†”表示矩阵的求逆运算。

2 所提算法

2.1 通过Nyström方法得到逼近的信号子空间

首先通过Nyström方法得到等效逼近的信号子空间，Nyström方法的本质是一种快速的“低秩矩阵逼近”算法之一，只用计算部分阵列输出数据所构成的协方差矩阵及对其特征分解就可间接获得逼近的信号子空间，避免了直接计算所有阵列输出数据所构成的协方差矩阵及对其直接进行特征分解，从而减少了运算量。由文献[13-15]可知，逼近的信号子空间可通过如下的Nyström方法得到。

将阵列输出X(t)=[x(t1),x(t2),…,x(tL)]分割成2个子矩阵：

(7)

式中，X1为由X的前q行组成的q×L维矩阵；X2为由X的后M-q行组成的(M-q)×L维矩阵。这里的q为一个定义的参数，需满足q∈{1,2,…,M}。2个子矩阵各自的协方差矩阵为：

(8)

(9)

式中，A1为由阵列流型矩阵A的前q行组成的矩阵；A2为其后M-q行组成的矩阵；RS为信号源的协方差矩阵。为了确保R11必须是一个满秩矩阵，则q应该大于信源数K且小于min(M,L)。通常，q的值无需随着阵元数M的增加而增加，当阵元数增加到较大时，依然可以选择一个较小的q值来分割矩阵，足以确保较准确的DOA估计以及同时减少计算量。在实际应用中，式(8)与式(9)的协方差矩阵R11，R21由下式估计得到：

(10)

(11)

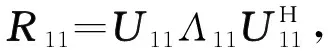
R21U11=U21Λ11，

(12)

(13)

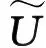
(14)

很容易证明上式特征向量矩阵U满足列矢量的相互正交特性，即UHU=I。且由协方差矩阵R特征分解得到的信号子空间US和近似特征向量矩阵U的前K列组成的矩阵张成同一空间，即span{US}=span{U(:,1:K)}[13]。

2.2 构建低阶特征方程进行DOA估计

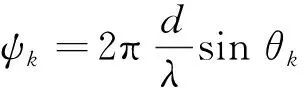
(15)

定义系数向量b=[b0,b1,…,bK-1]T及其构建的移位循环矩阵为：

(16)

对式(15)两边同时乘以ejJψk，可以得到如下齐次线性方程组：

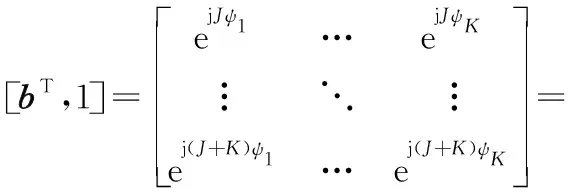
(17)

结合式(16)、式(17)及阵列流型A,有如下关系式成立：

BA=0(M-K)×1。

(18)

因为阵列流型A与信号子空间US张成同一空间，所以可以用信号子空间代替阵列流型，而本文用Nyström方法得到逼近的信号子空间UNS=U(:,1:K)，则用UNS代替阵列流型可得BUNS=0(M-K)×1。

同理，对式(15)两边同时乘以e-j(J+K)ψk,可以得到关于式(17)、式(18)的另一种共轭颠倒的齐次线性方程组及关系式：

(19)

(20)

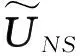
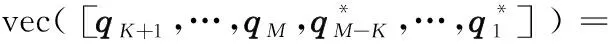
(21)

式中，vec表示矩阵的拉直运算，即把矩阵按照列的顺序，一列接一列地组成一个长向量。为了方便表示，用Ψ表示关于系数b的所有拼接组成的长向量构成的矩阵,即：

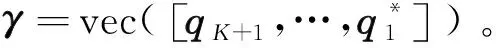
b=-Ψ†γ。

(22)

得到系数b后再代入式(15),通过求解此特征多项式的K个根αk(k=1,2，…,K)得到DOA估计如下：

(23)

式中，angle表示复数取相位角运算。可以看出，所提的新颖的DOA估计算法不同于现有的大多数DOA估计算法及求根DOA估计算法。现有的求根DOA估计算法利用了Pisarenko分解，利用MUSIC算法的噪声子空间与阵列方向向量正交的思想构建2(M-1)阶的多项式求根[17-18]，即：

(24)

式中，p(z)=[1,z,…,zM-1]T，z为信号传播到相邻两阵元时的相移，即z=ejψ。上式需要求解2(M-1)个关于单位圆呈镜像对称的根并最后选取K个在单位圆内离单位圆最近的根的相位给出DOA估计。而本文所提算法直接通过逼近的信号子空间构建一个阶数为K的低阶特征多项式方程并直接对求解得到的K个根提取其相位，得到DOA估计。相较于高阶多项式方程求解其计算效率更高。

3 计算复杂度分析

计算复杂度的衡量一般通过矩阵间的复乘次数来衡量。通过分析可知，MUSIC及ESPRIT算法需对所有阵列输出进行协方差的计算及对其特征分解得到信号或噪声子空间，所需的计算复杂度分别为O(M2L)及O(M3)。当MUSIC算法进行谱峰搜索得到DOA时，计算复杂度会随着搜索精度的提升而急剧增加，其谱峰搜索的计算复杂度为O(MKJ)，其中J代表搜索精度。而用求根MUSIC代替谱峰搜索时，相比谱峰搜索其计算量会大大下降，求根进行DOA估计时的计算复杂度为O((2(M-1))3)(若采用常规的多项式伴随矩阵特征值分解的方法来求解多项式的根[17])。而PM算法也需进行所有阵列输出的协方差计算O(M2L)，通过线性运算求得信号子空间的计算复杂度为O(M2K+MK2+K3)。本文所提算法无需对所有阵列输出计算协方差矩阵及特征值分解，经分析得知通过Nyström方法得到的逼近信号子空间的计算复杂度主要集中在块矩阵R11及R12的协方差矩阵计算上，其计算复杂度分别为O(Lq2)及O(MLq-Lq2)(q为定义的参数)。然后用基于Nyström方法构建信号子空间的计算复杂度为O(Mq2)[13]。可见，通过Nyström方法得到逼近的信号子空间总共的计算复杂度为O(MLq+Mq2)。通常有M，L≫K，则获取信号子空间这一步的计算复杂度就远小于上述算法。而获取低阶特征方程系数b所需的计算复杂度为O(2K(K+1)(M-K)+K3)[19]，最后求根进行DOA估计的计算复杂度为O(K3)，相较于求根MUSIC，其计算复杂度在求根环节要更低。若M≫K，则所提算法的整体计算复杂度主要集中在含有M的高阶项，即O(MLq)，而需计算阵列输出协方差及其特征分解算法的计算复杂度则主要为O(M3+M2L)。综上，所提算法具有较低的计算复杂度。几种算法的计算复杂度对比如表1所示。

表1 不同算法的计算复杂度分析

4 仿真实验及分析

这一节进行Matlab数值仿真实验来说明所提算法的有效性及进行性能对比分析。首先，说明验证了所提算法(Nyström-LD-root)对DOA估计的有效性。而后，与文献[11，19]所提的2种由PM算法衍生的快速估计算法PRM算法及PM-LD-rMUSIC算法进行了不同信噪比(SNR)及不同快拍数L下对算法估计性能影响的对比讨论分析。

4.1 DOA估计有效性验证

假设仿真实验中为一阵元数M=16的均匀线阵，阵元间距λ为半波长，SNR=10 dB，快拍数L=100，并设置参数q=8，有3个远场窄带非相干信号分别以波达角度θ为-30°,10°,20°入射到此阵列。进行50次独立实验得到的DOA估计如图2所示，可见在此仿真参数设置下所提算法能稳定地估计出DOA且每个角度的估计基本呈一条直线，则所提算法具有一定的有效性、可行性以及稳定性。

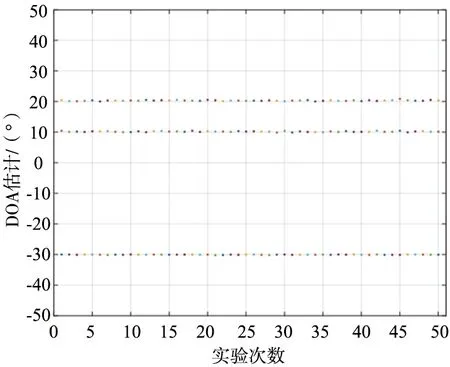
图2 DOA估计

4.2 信噪比变化对估计性能的影响

用均方根误差(RMSE)来衡量不同算法的估计性能，并做对比讨论。定义RMSE如下：

(25)

假设仿真实验中为一阵元数为M=12的均匀线阵，阵元间距d为半波长，快拍数L=500，设置所提算法的参数q取值8,10。有4个远场窄带非相干信号分别以波达角度θ为5°,15°,25°，40°入射到此阵列。SNR从5 dB以1 dB为步长增加至25 dB，对每一SNR进行500次蒙特卡罗仿真实验，在此仿真参数设置下对每一算法进行仿真并统计所得不同SNR下的RMSE对比如图3所示。

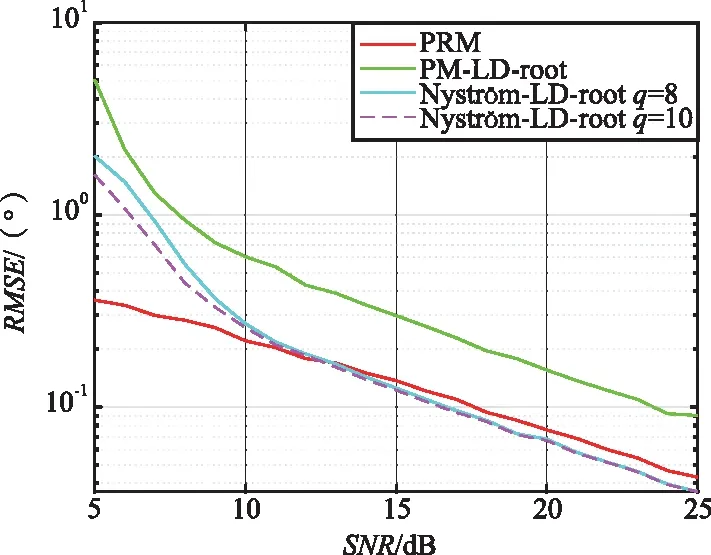
图3 SNR-RMSE对比

由图3可以看出，所有算法均随着SNR的升高其RMSE逐渐降低，但所提算法的RMSE要始终低于PM-LD-rMUSIC算法的RMSE，说明所提算法的估计误差要始终低于PM-LD-rMUSIC算法，估计精度较好。在较低SNR(10 dB以下)时，略逊于PRM算法的估计精度，因PRM算法结合了PM算法的快速估计信号子空间以及MUSIC-root算法的DOA估计精度高的特点，所以在低SNR时PRM算法的DOA估计误差要稍低一些。但在高SNR(13 dB以上)时所提算法的估计精度要好于其他2种算法。在高SNR时，对所提算法的Nyström方法中的q参数选取不是很敏感，在q取8或10时，其RMSE在高SNR时基本一致。因此，由上节计算复杂度分析可知，当阵元数M及快拍数L固定后在高SNR情况下，可选取一个适当较小的参数q来降低算法的计算复杂度。当在较低的SNR(10 dB以下)时，较大的q值可以提升一点估计性能。

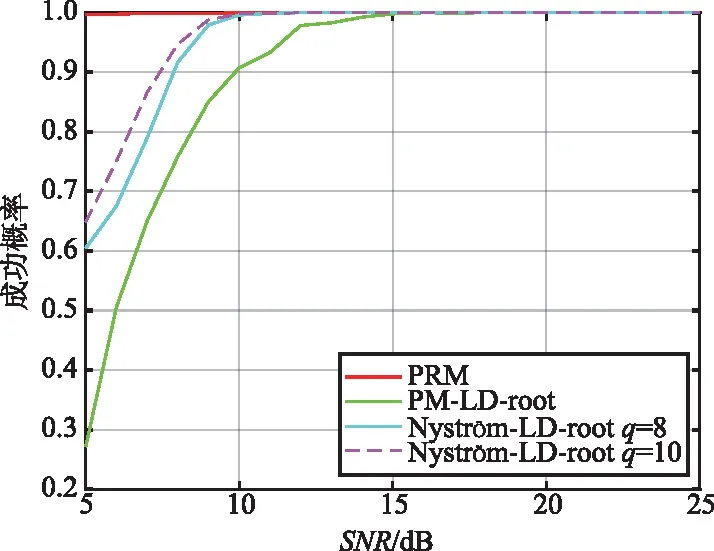
图4 不同SNR下的估计成功概率

4.3 快拍数变化对估计性能的影响

假设仿真实验中的阵元数M、阵元间距d、所提算法的参数q以及入射到阵列的信号波达角度θ依然与上一小节保持一致。快拍数L从100以100为步长增加至1 000，对每一快拍数L进行500次蒙特卡罗仿真实验，在此仿真参数设置下对每一算法进行仿真并统计所得分别在SNR=10 dB以及SNR=15 dB时的不同快拍数L的RMSE曲线如图5和图6所示，估计成功概率如图7和图8所示。

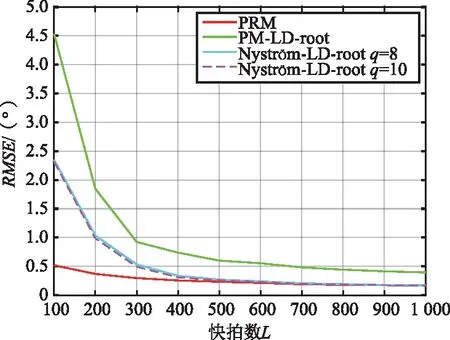
图5 信噪比为10 dB时不同快拍数的RMSE

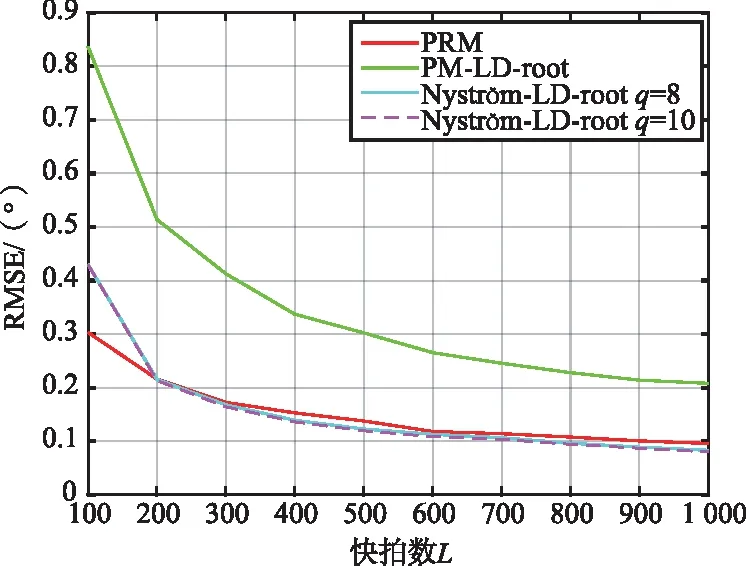
图6 信噪比为15 dB时不同快拍数的RMSE

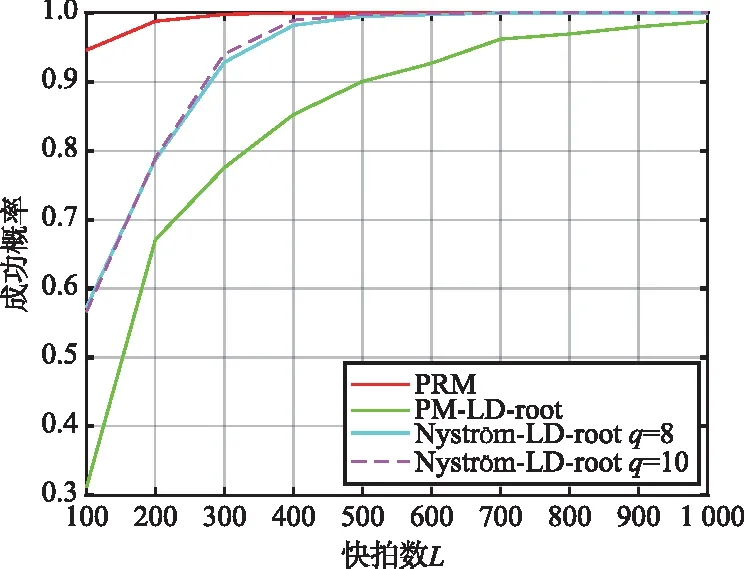
图7 信噪比为10 dB时的估计成功概率

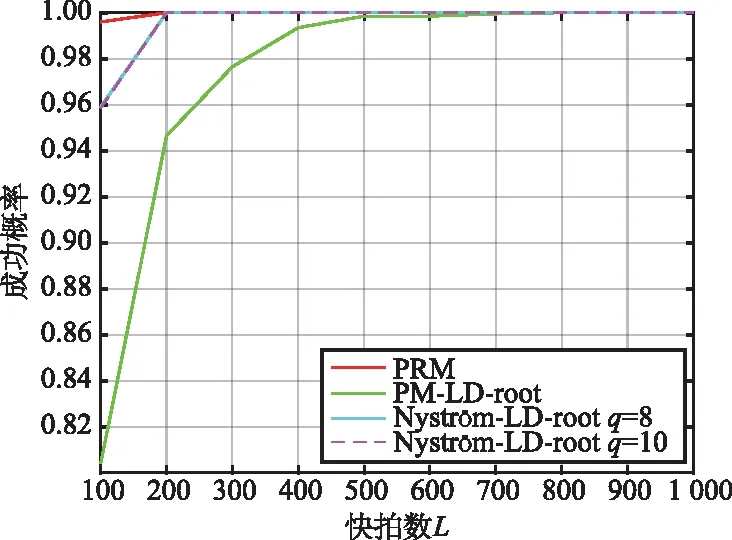
图8 信噪比为15 dB时的估计成功概率

由图5和图6可以看出，无论SNR如何变化，PM-LD-rMUSIC算法的估计误差随着快拍数的递增始终要大于所提算法。在较低SNR(10 dB)时，所提算法在快拍数400以上时与PRM算法的RMSE基本保持一致。而随着SNR升高到15 dB,所提算法在快拍数200以上其RMSE最低，估计误差要小于其余2种算法。说明在高SNR时只需较少的快拍数就可达到较好的估计精度。从图7和图8的估计成功概率图也可看出，所提算法在较低SNR(10 dB)时，在快拍数400多就可达到完全成功估计，而PM-LD-rMUSIC在快拍数1 000时还未达到完全估计成功。随着SNR升高到15 dB,所提算法只需200快拍数就可达到完全估计成功。从图5～图8也可看出，所提算法基本对参数q值的选取不敏感，在q为8，10的情况下，其RMSE曲线和估计成功概率曲线基本一致，估计性能渐进一致。

5 结束语

本文提出了一种低计算复杂度的新颖的DOA估计算法。首先通过Nyström方法得到逼近的信号子空间，无需计算所有阵列输出的协方差矩阵及对其特征分解，降低了计算复杂度。而后通过逼近的信号子空间直接构建关于DOA的低阶特征多项式方程，此低阶多项式方程的阶数仅与信号源数目相同，只需求解此方程的K个根就可得到DOA估计，提升了计算效率。仿真结果及理论分析表明，所提算法可对DOA进行有效估计且计算复杂度较低，在较高SNR时只需较少的快拍数就有较低的估计误差。