多径信道下基于CMA算法的SOQPSK-TG盲均衡

廖红姣，赖鹏辉*，董 蕤,王世练，张 炜，马艳敏

(1.国防科技大学 电子科学学院，湖南 长沙 410073；2.北京交通大学 电子信息工程学院，北京 100044；3.中国人民解放军31006部队，北京 100089)

0 引言

部分响应成形偏移正交相移键控(Shaped Offset QPSK，version TG，SOQPSK-TG)以其相位连续、包络恒定和频谱利用率高等优良特性，广泛应用于航空遥测领域中[1-3]，且被列入遥测IRIG 106标准[4]。

在“低仰角”场景下，遥测信号的传输会受到多径的影响[5]，信道均衡技术是一种常见的克服多径衰落的方法。由于航空遥测的信道特性复杂、线性均衡的效果不好，为了提高均衡有效性，Lucky[6]提出了自适应均衡技术。常用的自适应均衡算法可分为有训练序列的均衡和盲均衡算法。有训练序列的均衡算法包括最小均方(Least Mean Squares，LMS)[7]和递归最小二乘(Recursive Least Squares，RLS)[8-9]算法等，其收敛速度快、实时性好，但是需要人为插入训练序列。为解决上述问题需要占用额外频带资源，研究人员提出了盲均衡技术。

恒模算法(Constant Modulus Algorithm，CMA)[10]因其具有计算量小、良好的全局收敛性等特点，被广泛应用于通信系统中，文献[11]在理想同步下，对遥测多径信道使用CMA均衡进行了研究。本文针对遥测领域的3个典型“低仰角”场景，即滑行场景、起飞场景和远航场景，在非理想同步下，在同步和检测之前使用CMA完成盲均衡，评估SOQPSK-TG接收机中使用CMA抑制多径衰落的效能。

1 SOQPSK-TG信号

SOQPSK-TG信号的表达式为：

s(t)=ejφ(t;α)，

(1)

式中，φ(t)为相位；α为受限的伪三进制序列。当nT≤t≤(n+1)T时，φ(t)可以表示为：

(2)

式中，N表示符号间的关联长度，关联长度越长，主瓣越窄，复杂度越高。对于SOQPSK-TG信号，N=8。αk可以进一步表示为：

αk=(-1)k+1(2bk-1-1)(bk-bk-2)，

(3)

式中，bk表示输入的二进制比特流。

相位脉冲响应q(t)为：

(4)

式中，f(t)为频率脉冲，可以表示为：

(5)

式中，A为使脉冲积分为1/2的常数；B=1.25；ρ=0.7；ω(t)为窗函数，可以表示为：

(6)

式中，T1=1.5；T2=0.5。

2 基于CMA盲均衡的SOQPSK接收

2.1 CMA

CMA又称为Sato算法[12]，具有对接收信号载波频偏和相偏不敏感等特性[13]，被广泛应用于数字通信系统中[14]，算法的结构框图如图1所示。

图1 CMA系统框图

图1中，s(n)表示输入信号，z(n)表示加性高斯白噪声，e(n)表示误差信号，h(n)表示多径信道的信道冲击响应，可以表示为：

(7)

式中，L为传播的路径数；Γk为第K条路径相对于直射路径的反射强度，其值决定了各路径分量的相对功率大小；τk为第K条路径的时延。

CMA的代价函数JCMA表示为：

JCMA=E{|e(n)|2}=E{(|yn|2-R2)2}，

(8)

此代价函数是通过考虑均衡器输出信号与期望信号CMA圆的距离来执行均衡[15]，其中，R2为接收信号x(n)所在的CMA圆半径的平方，对于SOQPSK-TG信号，由于其具有连续相位的性质，可以表示为：s(n)=exp{jφ(n)}，所以，CMA圆的半径值为1，R2=1。y(n)表示均衡器的输出信号，可以表示为：

(9)

式中，W(n)为均衡器的抽头系数；XH(n)为接收信号的共轭转置。采用随机梯度下降法，迭代算法可以表示为：

wn+1(m)=wn(m)-μe(n)x*(n-m)，

(10)

式中，μ为迭代步长；x*(n)为接收信号x(n)的共轭；误差信号e(n)可以表示为：

e(n)=(|y(n)|2-1)y(n)。

(11)

2.2 SOQPSK-TG接收系统

SOQPSK-TG接收结构如图2所示，经采样、数字下变频后的基带数字接收信号x(n)直接进行CMA均衡，之后经过载波、定时同步和检测，同步、检测的具体细节参考文献[16]。

图2 SOQPSK-TG接收结构

3 信道模型和仿真结果

Rice等[17]在爱德华空军基地(AFB)描述了遥测多径信道模型。滑行场景、起飞场景和远航场景的多径信道统计数据被提出和应用在PCM/FM信号传输中[18]。本小节将发送信号分别通过3种信道，分析CMA均衡效能。

参考目前遥测链路实际情况，将SOQPSK-TG信号的速率设定为4 Mb/s，同时为了提升CMA均衡的有效性和收敛速度，CMA的参数选择为：步长0.000 2，滤波器抽头数121，滤波器中心抽头初始值0.8。

3.1 滑行场景

遥测飞行器降落在跑道上滑行时，地面障碍物多，发送端和接收端之间传输路径数较多；由于发送端和接收端相对位置变化较快，会产生多普勒频移。假定滑行场景的信道统计数据如表1所示。

表1 滑行场景信道模型

滑行场景中误差收敛曲线如图3所示。图中显示了滑行场景中均衡后在Eb/N0=30 dB的误差收敛曲线，其在迭代1 000次左右收敛，剩余误差为0.1。

图3 滑行场景中误差收敛曲线

滑行场景中误码率曲线如图4所示，显示了有均衡和无均衡2种情况下的误码率曲线对比。从误码率曲线可以看出，使用CMA均衡后，检测性能可以提升3～3.1 dB(BER=10-5)。

图4 滑行场景中误码率曲线

3.2 起飞场景

在起飞过程中，飞机飞行高度逐渐远离地面，多径环境参数如表2所示，与滑行场景相比时延更大、幅度衰减更大。

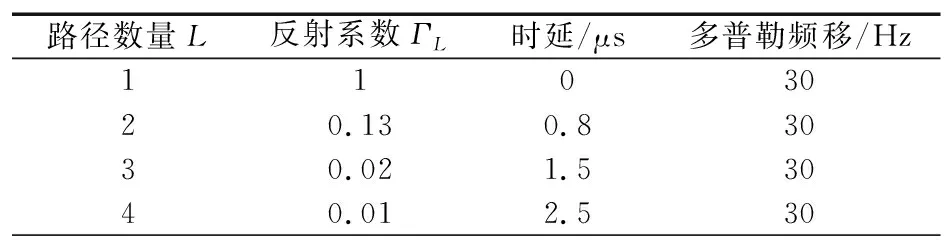
表2 起飞场景信道模型

起飞场景中均衡后的误差收敛曲线如图5所示，其收敛速度快，剩余误差小而稳定。

图5 起飞场景中误差收敛曲线

起飞场景中误码率曲线如图6所示。显示了CMA能提升0.9～1 dB(BER=10-5)的性能增益。

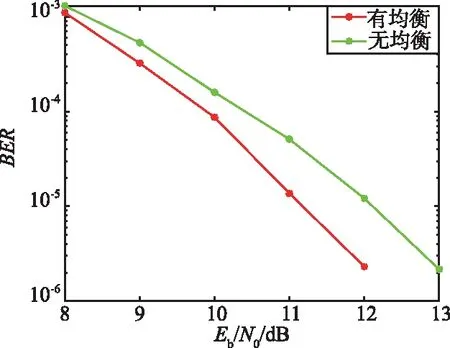
图6 起飞场景中误码率曲线

3.3 远航场景

远航场景中飞行器与地面距离较远，遥测链路可建模为双径模型，即一条直射路径和一条地面反射路径[5,18]，由于接收端和发射端的距离较远，地面反射路径与直射路径相比延迟较大，假定多径信道模型如表3所示。

表3 远航场景信道模型

当时延为4 μs时，相当于16个符号周期的延迟，此种场景下的多径干扰是3个场景中最严重的，当第2条路径的发射系数较大(Γ2=0.79)时，误差收敛曲线如图7所示。由图7可以看出，在此场景使用CMA均衡，其剩余误差较大。

图7 远航场景中误差收敛曲线(Γ2=0.79)

远航场景中误差收敛曲线(Γ2=0.40)如图8所示。由图8可以看出，如果不对信道进行均衡，即使Eb/N0达到20 dB，解调的误码率大于0.5，说明此时同步和检测进程无法正常工作，而对其进行均衡后，随着信噪比的增长，误码率呈现下降的趋势，Eb/N0=23.5 dB时，BER在10-5左右。当第2条路径的反射系数较小(Γ2=0.4)时，其剩余误差小而稳定，均衡可以提升10.8～11 dB的信噪比增益(BER=10-5)。远航场景中误码率曲线如图9所示。

图8 远航场景中误差收敛曲线(Γ2=0.40)

图9 远航场景中误码率曲线

4 结束语

在遥测领域中，滑行场景、起飞场景和远航场景的通信链路通常会受到多径干扰，CMA均衡应用于SOQPSK-TG接收可以在不占用多余频带基础上，有效地缓解多径干扰带来的码间串扰，从而提升解调性能。在滑行场景中，均衡可以带来3～3.1 dB的性能增益；在起飞场景中，均衡给接收机带来0.9～1 dB的性能增益；而在远航场景中，当第2条路径衰减较小时Γ2=0.79，无均衡时接收机无法正常工作，而对其进行均衡后，同步和检测才能正常工作，当第2条路径衰减较大时Γ2=0.4，其剩余误差收敛较慢，但均衡可以给接收机带来10.8～11 dB的性能增益。