复杂环境下基于序列Hough变换和逻辑法的航迹起始方法

薛俊杰，陈 剑，徐 恒，孟凡利

(上海航天电子技术研究所，上海 201109)

0 引言

Hough变换具有对局部缺损的不敏感、在随机噪声中鲁棒性等优点，因而在航迹起始中有广泛的应用[1-3]。基于Hough变换的航迹起始法采用阈值法对航迹进行检测，将探测到的点迹投影到参数空间中并进行积累，如若某个单元的积累值大于设定的阈值，就起始一条航迹，具有批量起始航迹的效果[4-5]。由于设定阈值要考虑杂波、噪声以及参数空间中参数选取的量化误差等因素的影响，因此阈值的选择存在两难的情况：① 阈值过低则参数空间中满足阈值条件的点就会变多，不仅会产生同一目标的多条航迹，而且会生成很多虚假航迹，加大了后续航迹还原的难度；② 阈值过高则可能出现目标在参数空间中积累达不到阈值的情况，特别是在低信噪比的环境下往往会发生漏检。因此为了尽量避免目标漏检，常用的方法是将阈值设置偏低[6]，但是查阅相关文献发现,在设置阈值时没有给出具体依据，因此方法的适用性不可知。另外，在目标对参数空间进行投票时没有考虑投票累加的有效性，常规Hough变换把多次扫描探测到的点都投影到参数空间中进行累加而没有考虑这些点在时间维上的差别，因此会出现一次扫描中的探测点在参数空间中累加次数超过1，明显与实际情况不符，且此时的累加显然没有任何物理上的意义。阈值过低同时也会导致在还原航迹时因为要回溯先前所有点迹并进行筛选，由于过阈值点数目太多导致运算量太大。特别在杂波密度大的情况下更为困难。因此，常规Hough变换在复杂环境下难以应用。

基于Hough变换和逻辑的航迹起始方法常运用于复杂环境下的航迹起始，但是由于其Hough变换结果为所有点迹(含杂波点)变换后的叠加，因此在目标航迹信噪比低的情况下其投票积累幅值受杂波分布的影响较大，从而很难在不同环境下选取合适、统一的阈值。一般情况下选用较低阈值会导致后续航迹还原的工作量变大。文献[7]采用多尺度Mean Shift聚类[8-9]与Hough变换相结合解决了航迹簇拥问题，但算法复杂度高且计算量大。文献[10]通过将点迹分类，高密度网格聚类低密度网格剔除减少杂波运算量，但是没有考虑密集杂波下雷达目标探测回波不连续，从而可能导致目标点剔除。本文提出的复杂环境下基于序列Hough变换和逻辑法的航迹起始方法可以有效减少复杂环境下无关杂波点在参数空间中的积累，同时文章的阈值设置方法避免了在回波不连续的情况下导致目标被杂波淹没的问题，采用的聚类[11-12]处理和点迹提取方法减少了复杂环境中航迹还原的计算量，最后通过构造复杂环境仿真场景验证了方法的有效性。

1 Hough变换原理

Hough变换法是通过式(1)将笛卡尔坐标系中的观测数据(x,y)变换到参数空间中的坐标(ρ,θ)：

ρ=xcosθ+ysinθ，

(1)

式中，θ∈[0,180°]。对于一条直线上的点(xi,yi)，则肯定存在2个唯一的参数(ρ0,θ0)满足：

ρ0=xicosθ0+yisinθ0。

(2)

在笛卡尔空间中的一条直线如图1所示，可以通过从原点到这条直线的距离ρ0以及ρ0与x轴的夹角θ0来定义。

将图1中直线上的几个点通过式(1)转换为参数空间的曲线，如图2所示。从图2中可以看出，图1中直线上的点转换到参数空间中的曲线后，这些曲线共同交于一公共点。这同时说明了，在参数空间中交于公共点的曲线所对应的笛卡尔坐标系中的坐标点一定是在一条直线上。

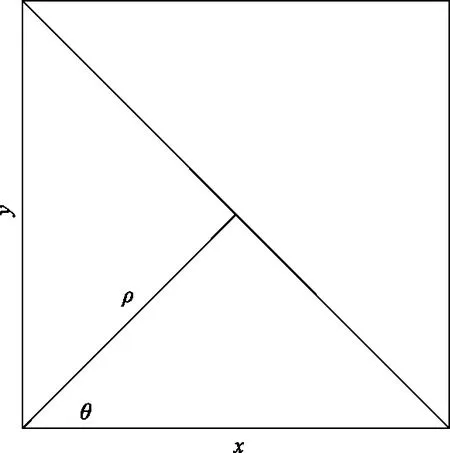
图1 笛卡尔坐标系中的一条直线

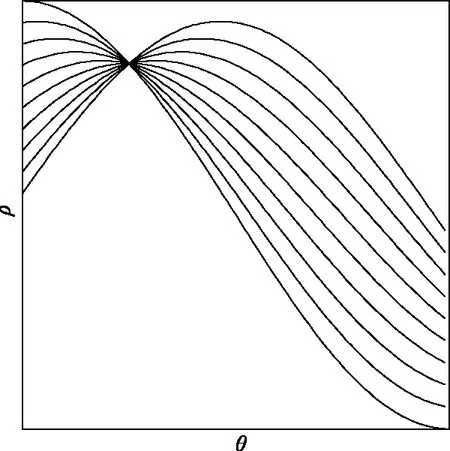
图2 Hough变换示意

(3)

(4)

式中，Δθ=π/Nθ，Nθ为参数θ的分割段数；Δρ=L/Nρ,Nρ为参数ρ的分割段数；L为雷达最大测量范围的2倍。当x-y平面上存在可连成直线的若干点时，这些点就会聚集在ρ-θ平面对应的区域内。对于直线运动的目标，在经过多次扫描之后，在参数空间特定单元中点的数量就会得到积累。然后通过设置门限阈值就可以从中检测航迹[13]。

2 基于序列Hough变换和逻辑法的航迹起始方法

基于Hough变换的航迹起始,在杂波多、目标信噪比低的环境下,航迹起始效果并不好,基本不能使用。因此大量文献都是对Hough变换进行修改后才使用，本文基于序列Hough变换和逻辑法的航迹起始方法能很好地在复杂环境下对航迹进行起始。算法示意如图3所示。

图3 算法示意

2.1 参数空间积累投票准则改进及阈值选取

Hough变换最早应用于图像处理中，图像中各个像素点没有时间先后顺序，所有像素点都变换到参数空间中的每个区域中并进行投票。设区域的投票数为K，则意味着有K-1个点共线。但是雷达扫描是有时间先后顺序之分，在一次扫描中目标只会出现一次且与该次扫描的其余点无关，因此不应与本次的其他点在参数空间上有累加。

基于上述考虑，本文每次扫描都定义一个参数空间的投票矩阵Ai(ρ,θ)，这次扫描的所有点都在这个矩阵上投票，但是对这个矩阵的任一区域应满足：

Ai(ρm,θn)≤1;m∈[1,Nρ],n∈[1,Nθ]。

(5)

设扫描次数为N，则最终的Hough变换投票矩阵为：

(6)

分别用标准Hough变换和本文采用的Hough投票方法对复杂环境下雷达5次扫描后产生的点迹进行变换，从图4标准Hough变换的投票结果可以看出，目标只出现5次的情况投票的峰值可达到20次之多，说明杂波严重地影响到了投票结果，最终导致无法准确设置阈值，因为显然设置不宜偏高，但是总共只扫描5次，若阈值设置为5，则可以看到不仅有相当多的点满足条件，后续进行航迹还原运算量巨大，无法进行，而且由于在复杂环境下目标回拨不连续，很有可能目标的积累值甚至达不到5，而阈值继续降低，无疑又增加了满足条件的投票点，导致后续运算更为恶化。

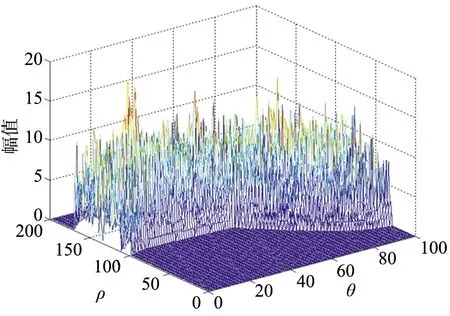
图4 标准Hough变换投票结果

图5为本文采用的Hough变换投票方法结果。可以看出，投票的峰值为5，结合M/N逻辑法准则，将M设置为投票的阈值，代表在N次扫描过程中至少有M次有点。一般来说M=N-1，即代表5次扫描中若有4次有点，则该处有航迹存在。同时可以看出，此时满足条件的投票点数仍然较多(少于标准Hough变换的投票结果)，但是在下面通过投票点聚类可以大幅度减少。

Q陈老师，您好！我儿子6岁3个月，今年9月份上小学，由于比较好动，专注力差，上课坐不住，而且零基础上学，经常挨老师批评，作业基本上都得回来我们手把手辅导，每天做作业得2个多小时。这样每天他的睡眠时间只有8个多小时。请问像现在这种情况我们该怎么办呢？孩子也有点厌学，我们也很焦虑。

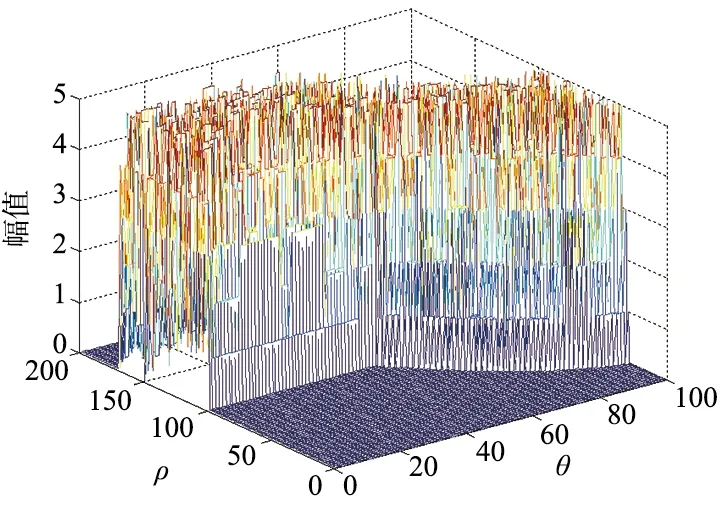
图5 本文Hough变换投票结果

2.2 有效点迹及投票点预提取

2.3 投票点聚类

在对一条直线上的多个点做Hough变换时，在理论的峰值(ρ,θ)点附近也会有较大的峰值出现，且峰值点呈蝶形分布[14]。速度1 000 m/s的Hough变换投票分布如图6所示。可以看到在交点附近，当目标速度与目标位置相比小很多时，蝶形分布退化为直线分布，如图7所示(目标位置与图6相当)。雷达目标运动速度与位置相比小很多，因此基本呈直线分布。

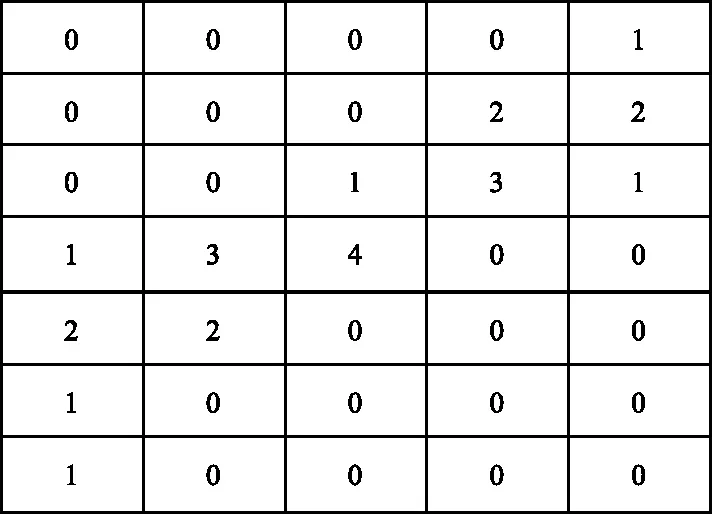
图6 速度1 000 m/s的Hough变换投票分布

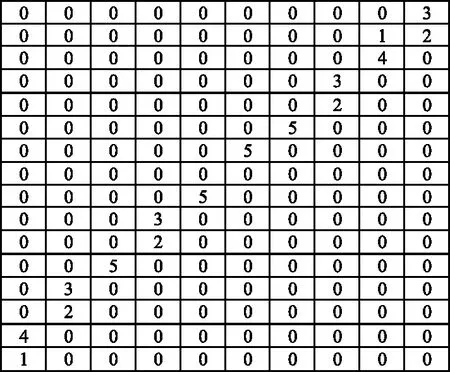
图7 速度200 m/s的Hough变换投票分布

因此通过2.2节，获得有效点迹及投票点队列后进行聚类处理，图8为经过2.2节提取出的点迹的(ρ,θ)分布情况，可以看到基本呈线分布，且许多点分布相近，而且这些点是顺序获得的，即队列中的θ值为递增的。

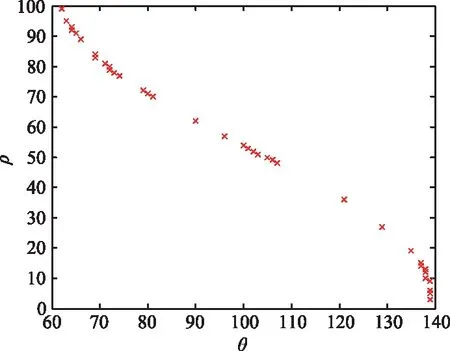
图8 目标点在杂波环境下的Hough变换投票分布

首先设置聚类相关的距离门限，由队列的第一个点开始遍历，将该点加入待聚类的队列中，若下一个点和该点距离小于门限，则将其也加入待聚类队列，直至遍历到超过距离门限的点。然后将待聚类队列中的所有点进行聚类处理，新的点位置取坐标均值并清空待聚类队列。将不满足聚类条件的点重新加入队列接着继续遍历，重复上述步骤直至结束。图9为聚类后的结果。可以看到，满足条件的点数量大大减少。

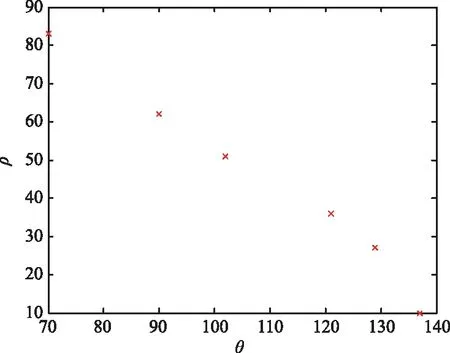
图9 聚类后Hough变换投票分布

2.4 航迹还原

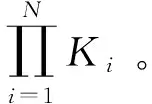
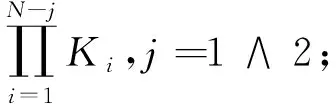
3 仿真结果及分析

3.1 目标数据

假定4个目标做匀速直线运动,使用2D 雷达对目标进行跟踪,4个目标的初始位置为(5 000,4 000)，(3 000,2 000)，(1 000,4 000)和(5 000,7 000),4个目标的速度为(200,200)，(100,-200)，(100,-200)和(300,0)。雷达的扫描周期为T=1 s,雷达的测向误差σx=σy=50 m,该雷达允许目标速度范围为50 m/s～3倍音速。

3.2 杂波产生

由文献[15]可知,在每个周期内的杂波个数可认为服从泊松分布[16]。因此,可以给定参数λ。首先在(0,1)区间上生成均匀分布的随机数γ,然后计算出J：

(7)

则J就是要产生的杂波个数。在确定J后,每个扫描周期内的J个杂波按均匀分布随机地分布在雷达视域范围内。

3.3 仿真结果及分析

仿真目标点迹示意图如图10所示。图10中，“+”代表第1次扫描时的点，“○”代表第2次扫描时的点，“*”代表第3 次扫描时的点,“□”代表第4次扫描时的点，“×”代表第5次扫描时的点。周期扫描数为5,参数空间的阈值为4，Nθ=100，Nρ=100，为模拟复杂环境下目标信噪比低的特点，将所有目标的随机一次扫描设置为丢失，即雷达的检测概率为0.8。为模拟复杂环境下杂波密度大的特点，参考文献[17-18]，将杂波数λ设为70。值得注意的是，本文仿真的范围为10 km以内，考虑到相关文献,仿真基本在100 km以内，因此在相同的杂波数下，本文仿真所设置的杂波密度要远大于参考文献。

图10所示的每条航迹都随机设置为扫描丢失一次。图11为雷达5次扫描点迹分布图，可以看出，目标航迹杂波十分密集，目标淹没在杂波中很难分辨出来。图12为点迹分布图上通过本文Hough变换后形成的航迹起始图(蓝色划线为形成的航迹)，表明本文采用的方法能够在密集杂波和回波不连续的情况下，排除杂波干扰的影响，成功起始出目标航迹。

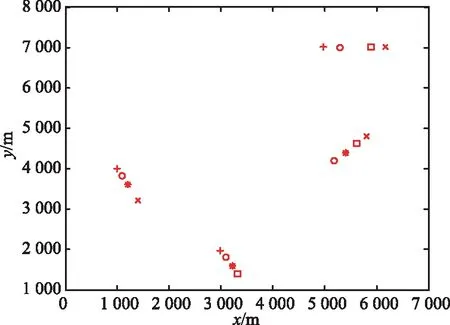
图10 仿真目标点迹示意

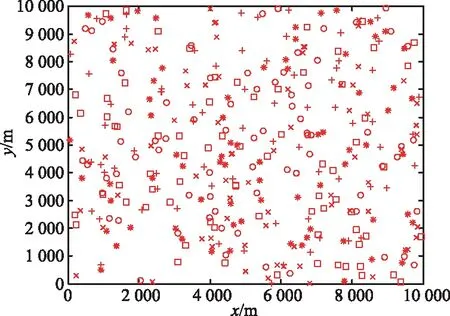
图11 雷达5次扫描点迹分布

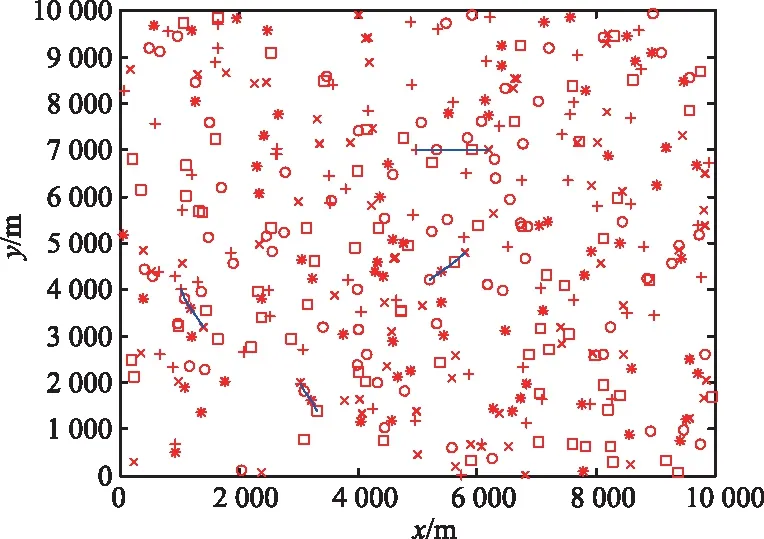
图12 航迹起始

4 结束语

针对复杂环境下航迹起始困难的问题，本文提出的基于序列Hough变换和逻辑法的航迹起始方法可以有效地在密集杂波大、雷达探测回波不连续的情况下起始航迹，仿真结果也验证了本文方法的有效性。展望下一步，算法仍有可以提高的空间，在算法的基础上对雷达探测到的点迹进行分区Hough处理，可以在更强杂波环境下进行航迹起始。