不同入射波对管束结构受力特性的影响
2022-04-21张志豪涂佳黄黄林茜吕海宇邓旭辉
张志豪,涂佳黄,2,黄林茜,吕海宇,邓旭辉,2
(1.湘潭大学土木工程与力学学院,湖南 湘潭 411105;2.岩土力学与工程安全湖南省重点实验室,湖南 湘潭 411105)
0 引 言
波浪与海岸结构的相互作用形式普遍可见,可以分为三种:波浪反射、波浪传播与越浪、波浪破碎。波浪与海上结构的相互作用现象也较为普遍,例如波浪与海洋管道、平台立柱等结构的相互作用,该类研究可以为以后实际工程应用提供一定的实用价值。在海洋工程中,海洋输油气管道并非仅由单圆柱型立管组成,其通常随注射液管道、电缆管道与单圆柱型立管一起安装形成三圆柱管束结构(triple-pipe bundle,TPB)。
目前,相关学者对波浪与结构相互作用的研究已取得一些进展,这些研究主要是针对波浪与单圆柱结构和其他结构的相互作用,而对波浪与TPB 结构相互作用的研究还需进一步深入[1-10]。Szmidt 与Hedzielski[1]使用光滑粒子流体动力学(smooth particle hydrodynamics,SPH)方法模拟了波浪作用下圆柱绕流的二维特性,主要对圆柱周围的流体流动进行离散化处理并计算沿圆柱圆周的压力分布与其所受波浪作用的合力;Wen 等[2-3]采用了SPH-LES 模型对三维波浪与海岸结构相互作用进行了研究,研究表明SPH 方法能够模拟大尺度的数值波浪水池并能较好模拟波浪与海岸结构的相互作用;Crespo 等[4]采用DualSPHysics 无网格化程序模拟了海面波浪与海洋立管相互作用,并将SPH 模型与实验结果进行了对比;Altomare 等[5]采用SPH 微可压缩模型研究了二阶长峰波与随机波的产生以及反射波吸收系统(被动粘性消波与主动消波)工作性能,同时还研究了波浪与结构的相互作用,将结构物所受的波浪力时程变化与实验结果进行了对比;随后,Altomare 等[6]与曾冬[7]基于SPH 方法对波浪与结构相互作用力进行了研究,并与Sanflous、Goda、Takahashi 等理论计算公式[8]结果进行了对比验证,研究发现模拟结果与理论计算结果以及已有实验数据基本吻合。除了SPH 方法以外,Hu 等[9]基于开源程序OpenFOAM 分别对数值波浪与主动吸收波系统及波浪与柱体结构相互作用进行了研究;Zhang 等[10]采用包含单元均值和点值(volume-average/point-value method,VPM)的有限体积法求解Navier-Stokes 方程和具有二次曲面性质和高斯积分的双曲正切函数(THINC method with quadratic surface representation and Gaussian quadrature,THINC/QQ)方法对黏性数值波浪水池进行了模拟,研究表明在相同的网格大小或时间步长条件下,VPM-THINC/QQ 模型在波浪数值耗散方面控制较好且无相位差。
基于SPH算法,本文对三维数值水池模型及波浪与垂直圆柱相互作用两个问题进行验证对比,以验证本方法对波浪运动特性模拟的精确性与可靠性。然后运用该方法对波浪与垂直TPB结构相互作用问题进行探究,并重点分析了不同旋转角度(α)与不同波参数对结构所受波浪力的影响,并引入单圆柱体结果进行对比分析。
1 SPH数值方法
1.1 SPH理论
SPH 是一种拉格朗日无网格计算方法,其通过一系列任意分布的粒子来表示问题域[11]。在SPH方法中,用积分近似场函数,即核近似法(kernel approximation),近似函数F(r)可写为
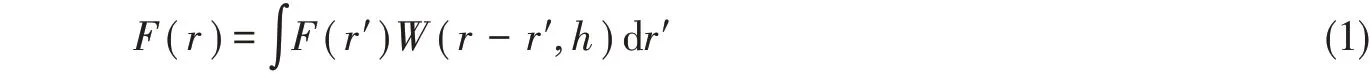
式中,W为光滑核函数,h为光滑长度,r是粒子矢量位移。式(1)可以进一步离散化,其中函数的近似值可在给定位置(或粒子a)处内插得到,并且对内核紧支域内的所有粒子进行叠加求和:
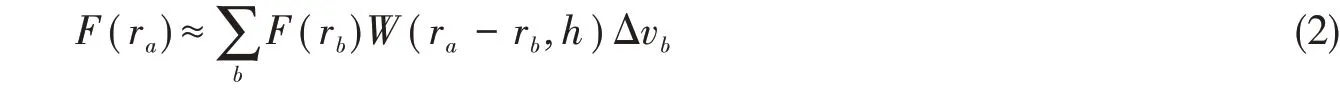
式中,a表示一个孤立的粒子,Δvb表示临近粒子b的体积,且光滑核函数满足

SPH 的模型对光滑内核函数的选择较为严格,内核可以表达为粒子之间的无量纲距离,即q=r/h,其中r是任何两个给定粒子a和b之间的距离,h控制粒子a周围的区域尺寸,该区域要考虑相邻粒子。在尺寸大小为2h的影响域内采用Wendland四次插值光滑核函数:
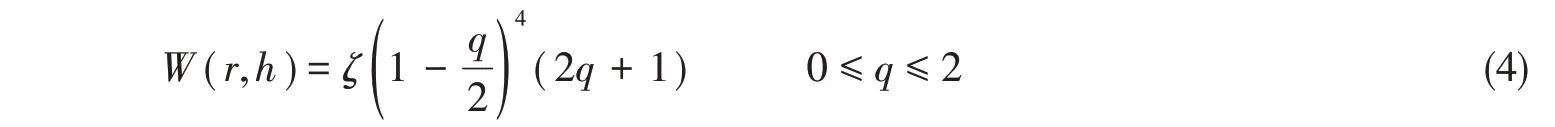
式中,ζ为修正系数,取值分别为7/(4πh2)(二维模型)与21/(16πh3)(三维模型)。
1.2 控制方程
SPH方法中的动量方程可以写为
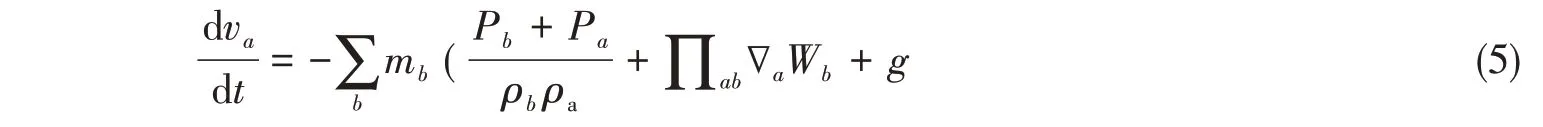
式中,Pa与Pb分别表示粒子a、b的压强,ρa与ρb分别表示粒子a、b的密度,其中g为重力加速度。粘度项∏ab可以进一步表示为
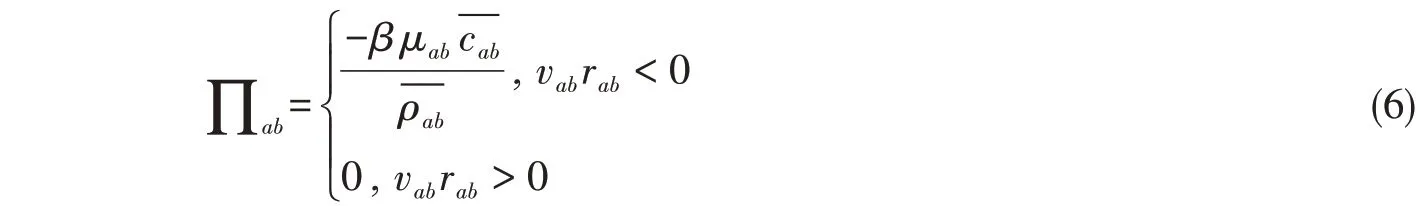
式中,rab=ra-rb,vab=va-vb以及vk、rk分别表示粒子k的速度与位移;μab是平均声速,β是确保正常粘性扩散而引入的修正系数。
SPH方法中,用于计算相应密度变化的连续性方程为

由于SPH 方法中的流体被视为弱可压缩的,可用状态方程确立粒子密度之间联系进而求得流体压力为

式中,ρ0=1000 kg/m3是流体表面的相对密度;γ是几何常量,取值范围为1~7;参数B=c2ρ0/γ与流体的压缩性相关,其中c为相对密度下的声速。时间步Δt的取值由克朗数条件(Counrant-Freidrich-Levy condition)、压力项以及粘性扩散项决定,本文所有的计算模型克朗数设定为0.2。
1.3 边界条件
SPH 方法中,边界由一组独立的流体粒子所组成。Crespo 等[12]提出动态边界条件,该边界的粒子不仅能满足与流体粒子相同的运动方程,还能保持固定位置或者根据预先定义的运动函数进行运动。当流体粒子接近边界粒子时(即两者之间的距离小于2倍光滑半径h),受到影响的边界粒子的密度将增大,导致边界粒子压力增大。同时,由于动量方程中的压力项存在,边界粒子会对流体粒子产生排斥力。数值水池上游边界处采用动态边界条件,下游设置粘性消波区。同时,侧边边界条件采用周期性边界条件进而消除边界粒子附近的数值耗散问题[13]。
2 造波理论
由于Madsen 的二阶造波理论计算可靠、简单易实现,且有足够的精度[14],因此本文采用该理论模型。为了消除波浪在传播过程中反射波的影响,在本文所有数值模型中采用了被动消波处理,即在下游处设置固定尺寸的人工粘性消波区。
对于二阶Stokes波,其造波板运动振幅S0与波高H之间关系为

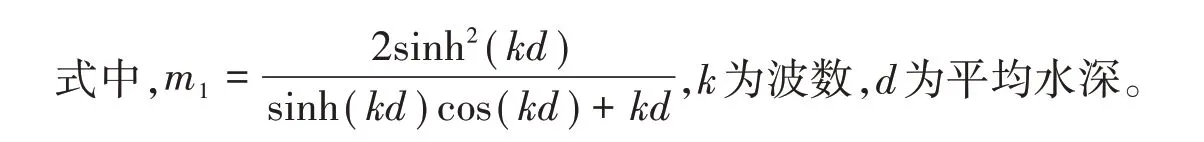
根据Madsen理论,二阶规则Stokes波造波板位移运动函数e(t)的表达式如下:
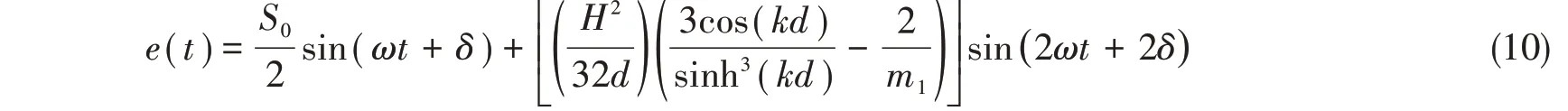
式中,δ为初始相位,ω为圆频率,第一项为一阶线性波的位移运动函数,第二项为二阶位移运动函数外加项。
3 算例验证
3.1 波浪运动特性验证
本节对三维数值水池模型进行了计算并验证了SPH方法数值造波的可靠性。三维波浪水池模型尺寸为12 m×2 m×1 m(长×宽×高),初始静水位为0.5 m,造波板距离上游边界0.2 m,在距上游边界9 m处设置了3 m长的粘性消波区,如图1(a)所示。入射波采用了Stokes二阶规则波,其波高与波周期分别为kH=0.367与T=1.2 s。图1(b)给出了t/T=10时刻的三维波面图,由图可知该入射波的二维特性较为强烈以及粘性消波区消波效果较为理想,同时发现波面沿程耗散性较小。另外,图2给出了不同粒子间距下,特定位置处自由液面与速度值的时程曲线,由图可知三种不同粒子间距对其结果的影响较小。考虑到计算资源的消耗性与求解模型的可靠性,设置初始粒子间距为dp=0.02 m以及光滑长度取1.5dp,总粒子数约为160 万。图3 分别给出了x=5 m 处的自由液面高度时程曲线及x=6 m 处波速分布与Stokes 二阶理论解的对比结果。从图3(a)可知,SPH 模拟的自由液面高度值变化与理论结果较为吻合,两者无明显的相位差且其脉动性相差较小。另外,从图3(b)可知,SPH模型所得的波速时程分布与理论值结果基本一致,这进一步说明了本方法的可靠性与适用性,能够较好地模拟波浪运动特性。
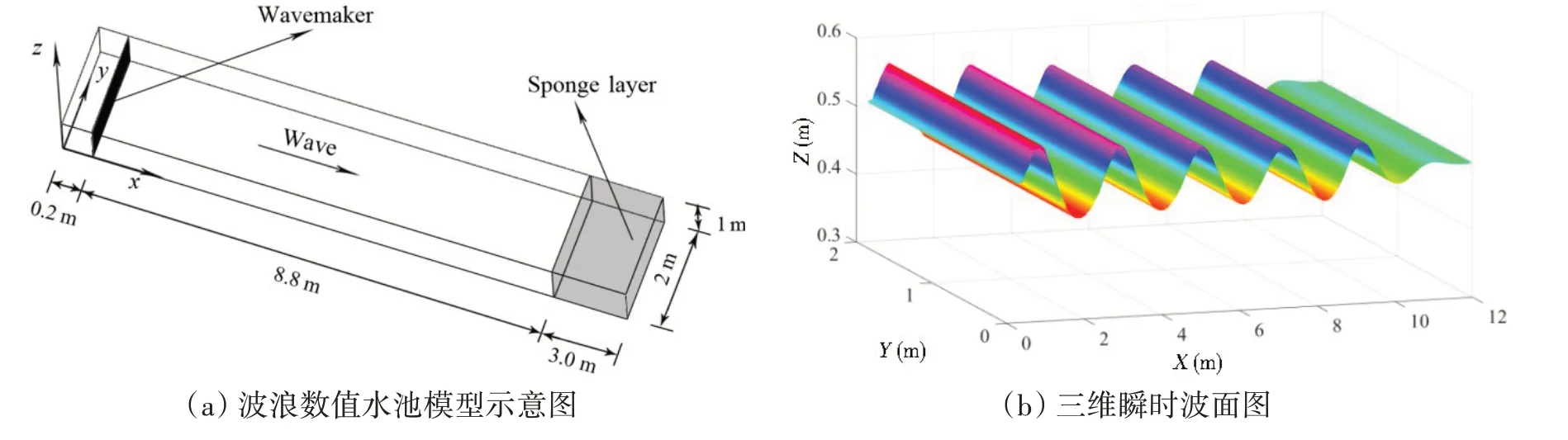
图1 波浪水池模型尺寸大小与三维波面图Fig.1 Numerical wave basin and instantaneous 3-D wave
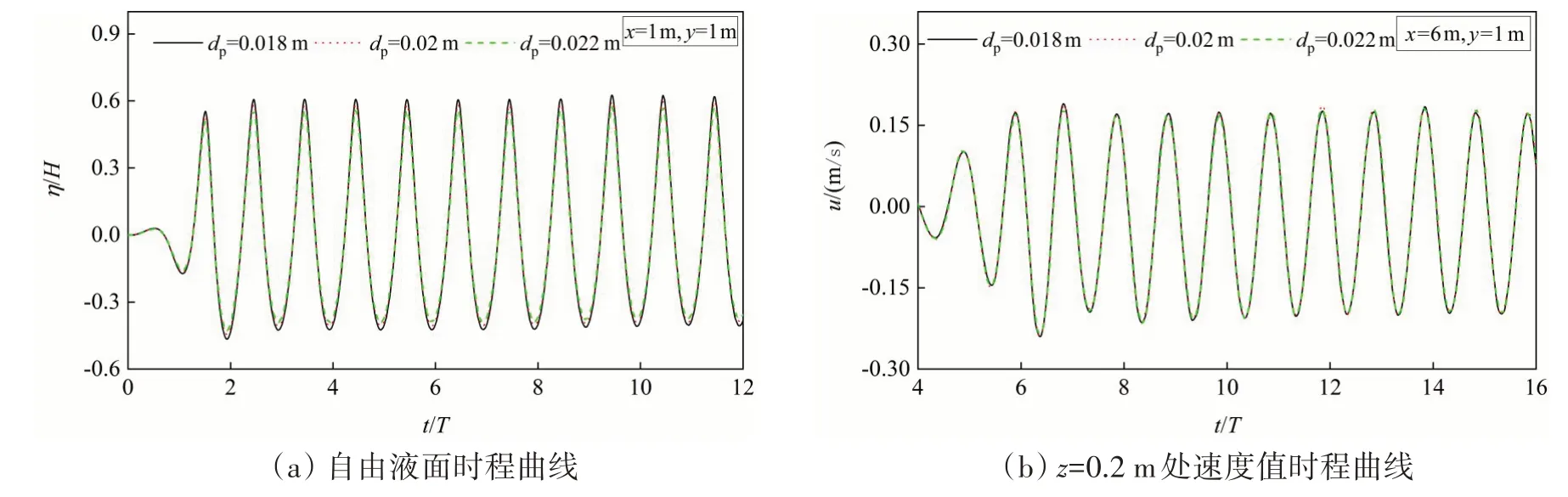
图2 不同粒子间距下,自由液面与速度时程曲线Fig.2 Time history of the water surface profiles and wave velocity with different particle spacings
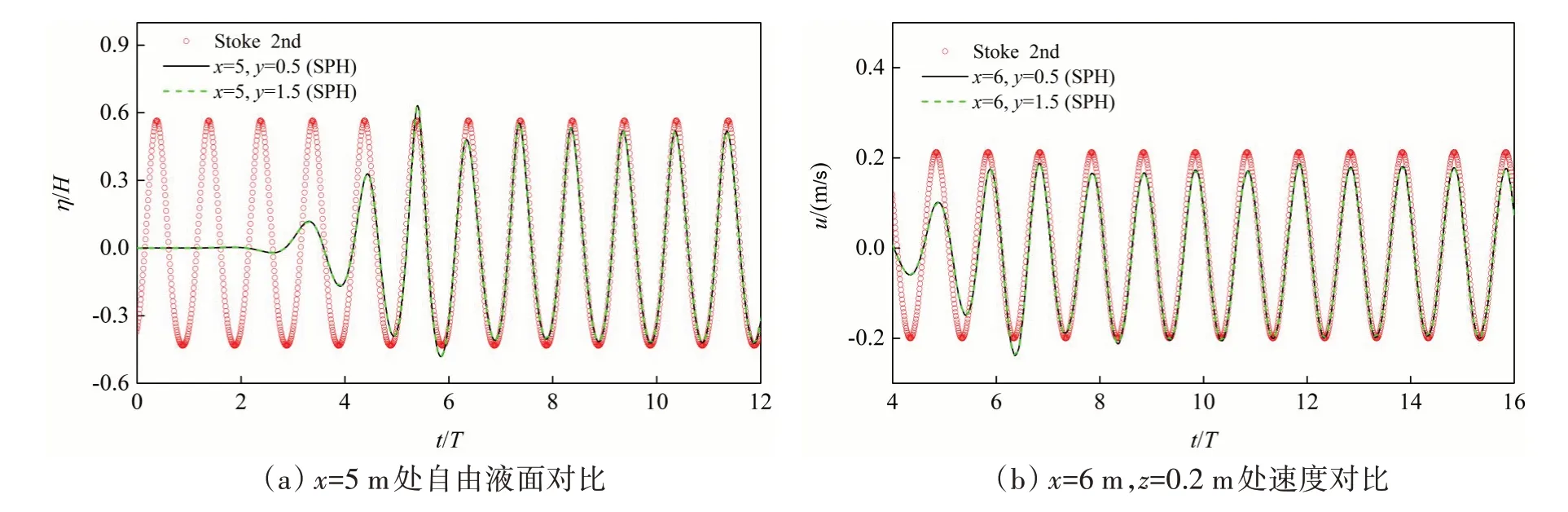
图3 不同位置处的自由液面高度与速度变化曲线与理论解的对比Fig.3 Comparison of the computed and analytical water surface profiles and velocities at different measuring points
3.2 波浪力验证
对单圆柱体所受波浪力进行了数值计算并与相关文献结果[9,15]做了对比分析。该验证模型关于波浪与单圆柱体的主要参数可见表1,其中数值水池的尺寸为12 m×1.2 m×0.9 m,圆柱体直径为D=0.325 m。柱体中心的位置与造波板距离约为一个波长,在数值水池的下游处设置3 m 长的粘性消波区,见图4。对波浪力进行了无量纲化处理,即Fx/F0,其中F0=0.5ρgDHd[tanh(kd)/d],参数D为圆柱体的直径,ρ为水体密度以及g为重力加速度。

表1 验证算例模型相关参数Tab.1 Validation parameters of the model
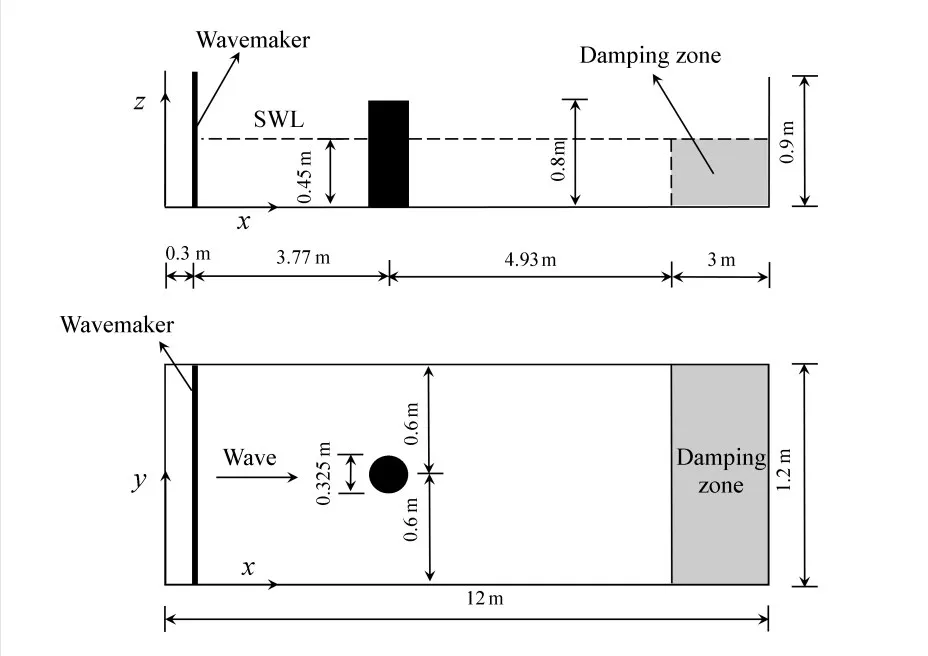
图4 波浪对单圆柱体作用计算模型Fig.4 Numerical model setup of the wave and cylinder interaction
图5分别给出了SPH 模型单圆柱体所受波浪力时程变化与一个周期内波浪力的时程变化与二阶理论解、模拟结果与实验结果的对比。从图5(b)可知,本文的数值结果与二阶理论值以及OpenFoam求解结果较为吻合,其中与实验结果的对比在数值上存在细微误差,但两者的变化趋势基本一致。因此,这进一步论证了SPH 方法对波浪与结构相互作用模型求解的可靠性与正确性。另外,SPH 求解模型中共设置了三种不同粒子间距工况(dp=0.018 m、dp=0.02 m 与dp=0.022 m),可知三种不同粒子间距的模拟结果相差较小,变化趋势基本一致。
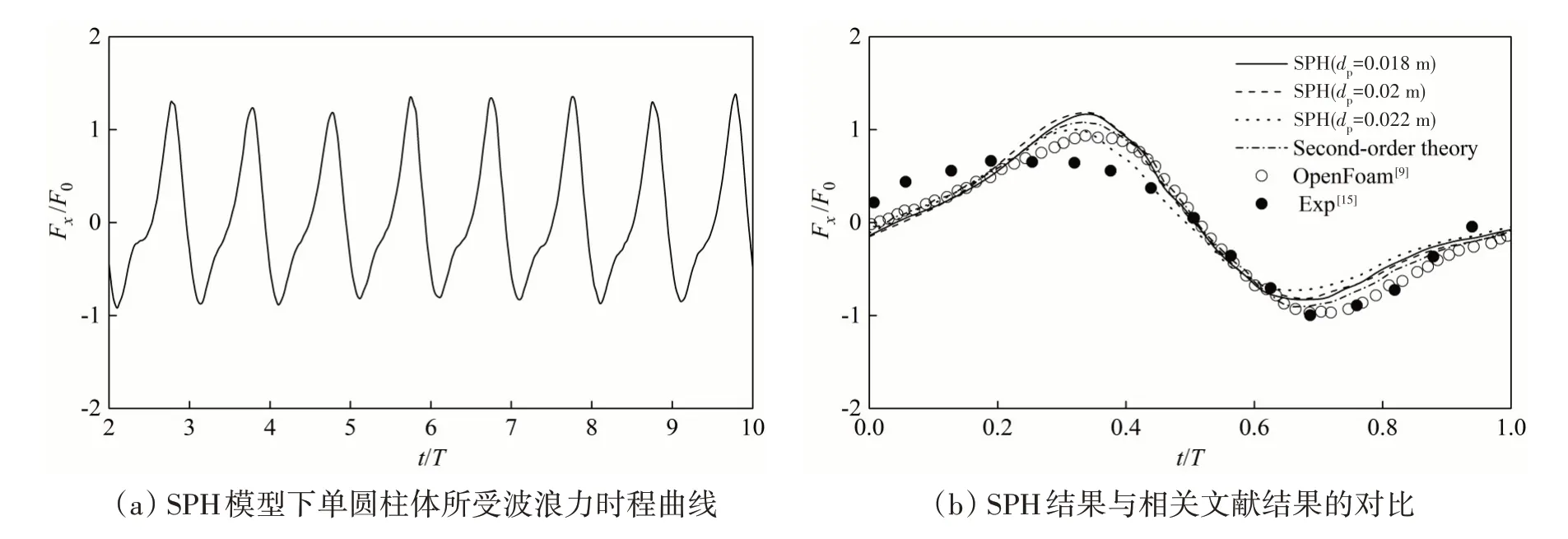
图5 单圆柱体所受波浪力时程曲线及其与现有文献结果的对比Fig.5 Time history of the wave force and comparison of the normalized horizontal force on circular cylinder with literature results at one wave period
4 问题描述
运用SPH 方法对Stokes 二阶规则波与圆柱体的相互作用进行了计算,对数值水池不同计算域宽度(y/D=7.5~15)对波浪力的影响进行了比较分析,如图6 所示。在进行分析前,对波浪力与最大波浪力先进行无量纲处理,具体形式分别为F/(ρgHD2/8)与Fmax/(ρgHD2/8)。从图6(a)可知,不同计算域宽度的波浪力时程曲线并未出现显著的相位差,但是对波浪力的脉动性有一定影响。图6(b)给出了不同计算域宽度对最大波浪力的影响,其中计算域宽度y/D=7.5的最大波浪力与y/D=12.5工况的结果最大相差16.7%,而计算域宽度y/D=10 的最大波浪力与其仅相差3%。因此,本文所有计算工况的计算域宽度可选为y/D=10。
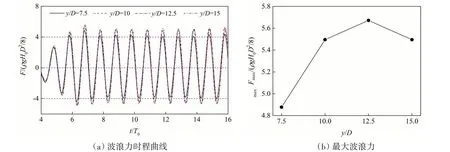
图6 不同计算域宽度对圆柱体所受波浪力大小的影响Fig.6 Effect of different calculation domain widths on the wave force on circular cylinder
因此,本文所采用的数值水池尺寸为12 m×4 m×1 m,单圆柱体与TPB 结构主圆柱体直径均为D=D0=0.4 m。圆柱体与TPB结构主体中心位于距离造波板位置6.3 m 处,且该距离大于3倍的波长,以减少结构表面产生的反射波对造波板干扰作用[16]。在下游边界处设置了3 m长的粘性消波区,静水位高度为d=0.5 m,柱体高度为0.8 m。造波板位于距上游边界0.3 m处,其厚度固定为5倍的粒子间距。另外,本章数值水池与单圆柱体、三圆柱管束结构相互作用示意图与3.2节中的图4一致,其中TPB 结构尺寸示意图与不同旋转角度示意图见图7。表2列出了TPB 结构具体的尺寸参数值,其中主圆柱体直径为0.4 m,中间圆柱体直径为0.2 m,小圆柱体直径为0.1 m。

表2 三圆柱管束结构几何尺寸Tab.2 Geometry of triple-pipe bundle
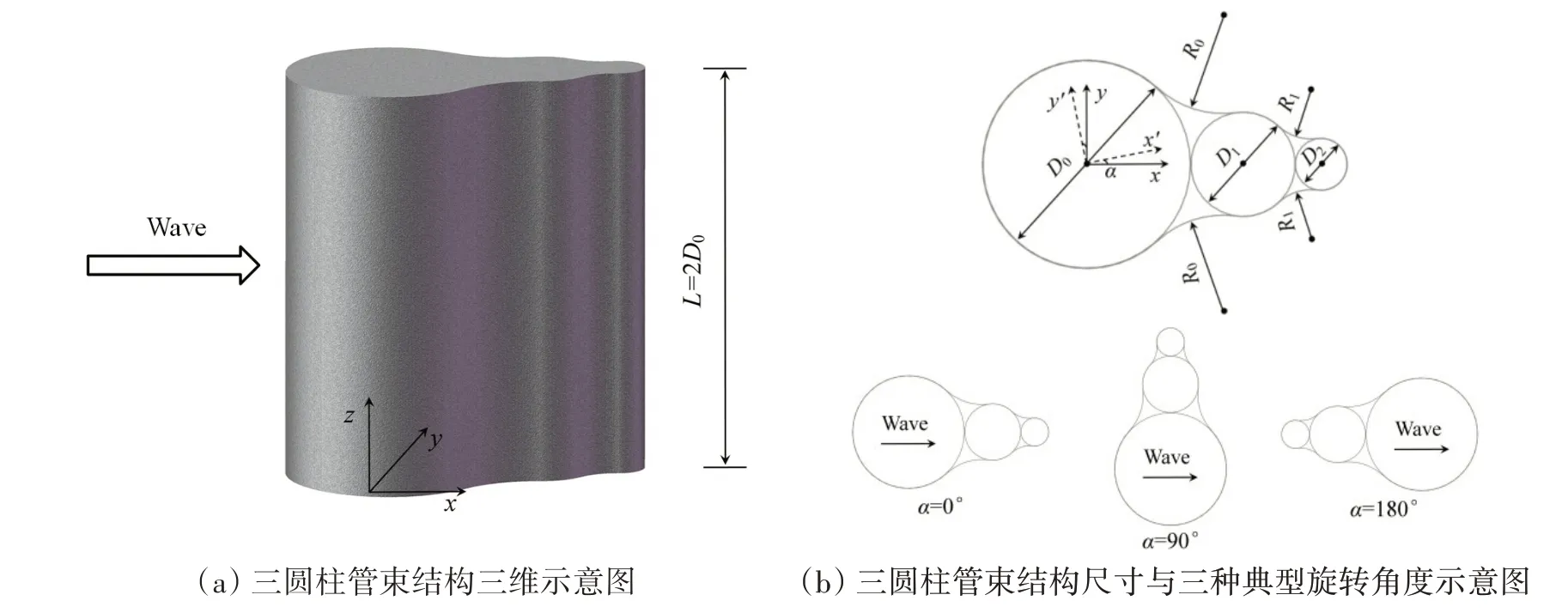
图7 三圆柱管束结构示意图Fig.7 Schematic diagram of the arrangement of the triple-pipe bundle
另外,为方便描述相关工况的计算结果,定义一个基本波况Wave0,基于Wave0 分别分析了五组不同波周期(T=1.0~1.8 s)与五组不同波高值(kH=0.122~0.367)的入射波对单圆柱体受力特性的影响,同时对不同水深(kd=1.224~1.836)的影响也进行了分析。表3 给出了Wave0 的具体波形参数,其中Wave0 工况的周期以T0表示,波高以H0表示,本文所有的数据无量纲结果均基于T0与H0,所有工况的总模拟无量纲时间为t/T0=16。

表3 基本波况参数Tab.3 Parameters of basic wave
5 结果分析
5.1 不同旋转角度对管束结构受力特性分析
基于基本波况Wave0条件下,对9组不同旋转角度(α=0°~180°)的TPB结构受力特性进行了研究,同时引入单圆柱的计算结果作为对比,如图8~9 所示。图8 给出了单圆柱与TPB(α=0°)所受波浪力时程曲线对比结果,可知两者波浪力脉动性几乎一致,但存在较小的相位差现象。这主要是由于TPB 结构在α=0°工况下,波浪对其迎流面处的冲击作用大小与单圆柱相接近。两者之间较小的相位差主要由两者的结构物与波浪接触面积的差异性所致。
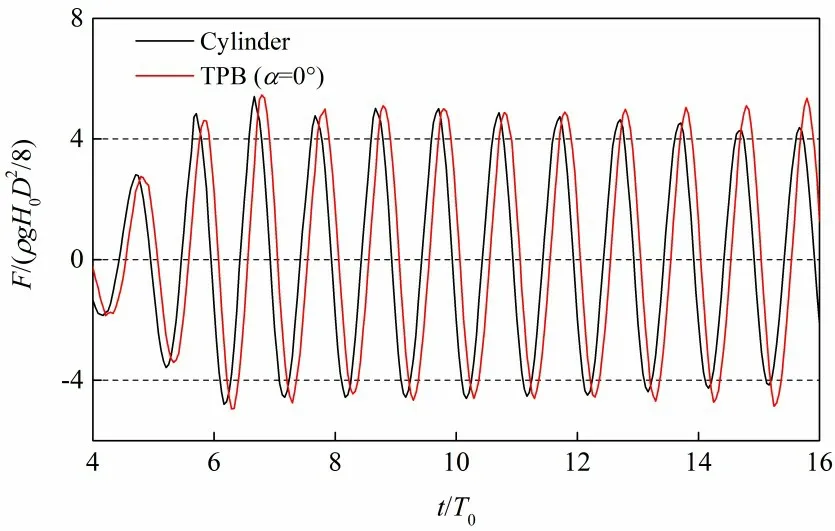
图8 圆柱体与TPB结构所受波浪力时程曲线变化Fig.8 Comparison of wave force time history on cylinder and TPB
从图9(a)可知,不同旋转角度下TPB结构所受波浪力的变化有较大差异,各角度工况的波浪力时程曲线并未出现明显的相位差。值得注意的是,TPB结构在旋转角度为90°时所受波浪力脉动性最大,在180°转角时所受波浪力脉动性最小,其最大波浪力随α增加呈现出相同的变化趋势,如图9(b)所示。事实上,这主要是由于TPB结构在90°工况时,迎流面受入射波冲击作用区域增大进而导致其受力较大。同样地,TPB结构在180°时迎流面与入射波浪的接触面较小导致其受力较小。另外,最大波浪力随TPB结构旋转角度变化,先呈现逐渐增大的趋势,在90°达到最大值,随后又迅速地减少,如图9(b)所示。
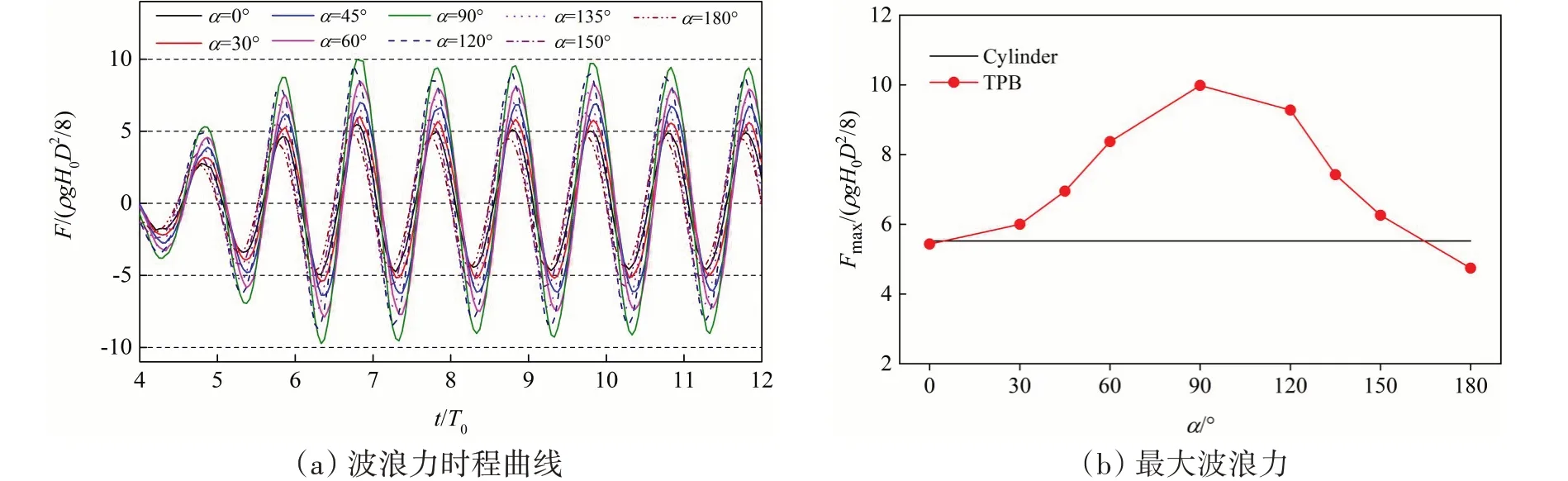
图9 不同旋转角度TPB结构的波浪力变化特性Fig.9 Wave force change of TPB structure at different rotation angles
5.2 管束结构附近流场速度分析
本节以TPB 结构旋转角度为90°工况为例,探究波浪与TPB 结构相互作用的水动力特性。图10给出了不同时刻三维波浪与TPB 结构相互作用流场示意图,并用波速值的大小对波面进行了渲染处理。为方便分析,特此给定了波峰即将运动到TPB迎流面处时刻(t/T0=7.71)、波峰正穿过TPB时刻(t/T0=7.92)、波峰即将穿过TPB 时刻(t/T0=8.13)与波峰刚好穿过TPB 时刻(t/T0=8.33)的波浪与结构相互作用示意图。从图10可知,TPB结构对波浪的运动具有一定的阻碍作用,同时波浪运动经过结构时会发生绕射现象,此时波能将沿着波峰线从高能流域传递至低能流域。在t/T0=7.92与t/T0=8.13时刻(见图10(b)、(c)),结构周围发生明显绕射现象,且其上下两侧附近处的速度值较大,表明此时TPB 结构两侧受到波浪较为强烈的冲刷作用。特别地,如图10(a)所示,可观察到TPB 结构迎流面处产生与波浪传播方向相反的反射波,并且该反射波会影响下一个波峰的运动特性。除此之外,图10 中也可明显观察到数值水池下游粘性消波区速度值大小几乎接近于0,这进一步说明了该数值水池的粘性消波区具有较好的消波效果。
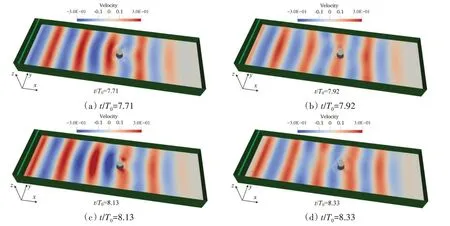
图10 Wave0工况下,不同时刻三维波浪对圆柱体作用流场速度分布图Fig.10 Distribution of flow field velocities of the interaction between wave and cylinder with Wave0 at different times
5.3 管束结构周围涡量分布
从5.1 节分析中可知,TPB 结构在α=90°时所受最大波浪力最大,在α=180°时所受最大波浪力最小,在α=0°时所受最大波浪力与单圆柱体工况接近。为了进一步分析其中所受波浪力的水动力特性原因,图11 给出了俯瞰视角下,不同时刻三种不同旋转角度工况下的TPB 结构周围表面流体粒子涡量(ωx)分布,并且与单圆柱体结果进行对比。同样,为方便分析,特此给定了三种不同时刻(t/T0=7.67、8.0、8.33)的结构周围涡量分布图。从图可知,单圆柱体周围的涡量沿着柱体表面两侧呈现对称分布,且两侧涡运动方向相反。另外,随着波浪运动单柱体两侧的涡量分布区域基本保持稳定状态,表明柱体两侧受到波浪冲刷作用较为强烈。对于TPB结构,除了在结构壁面处具有显著涡量分布外,离壁面不远处的周围区域也存在一些紊乱分布的涡,这与单圆柱结果有较大差异。
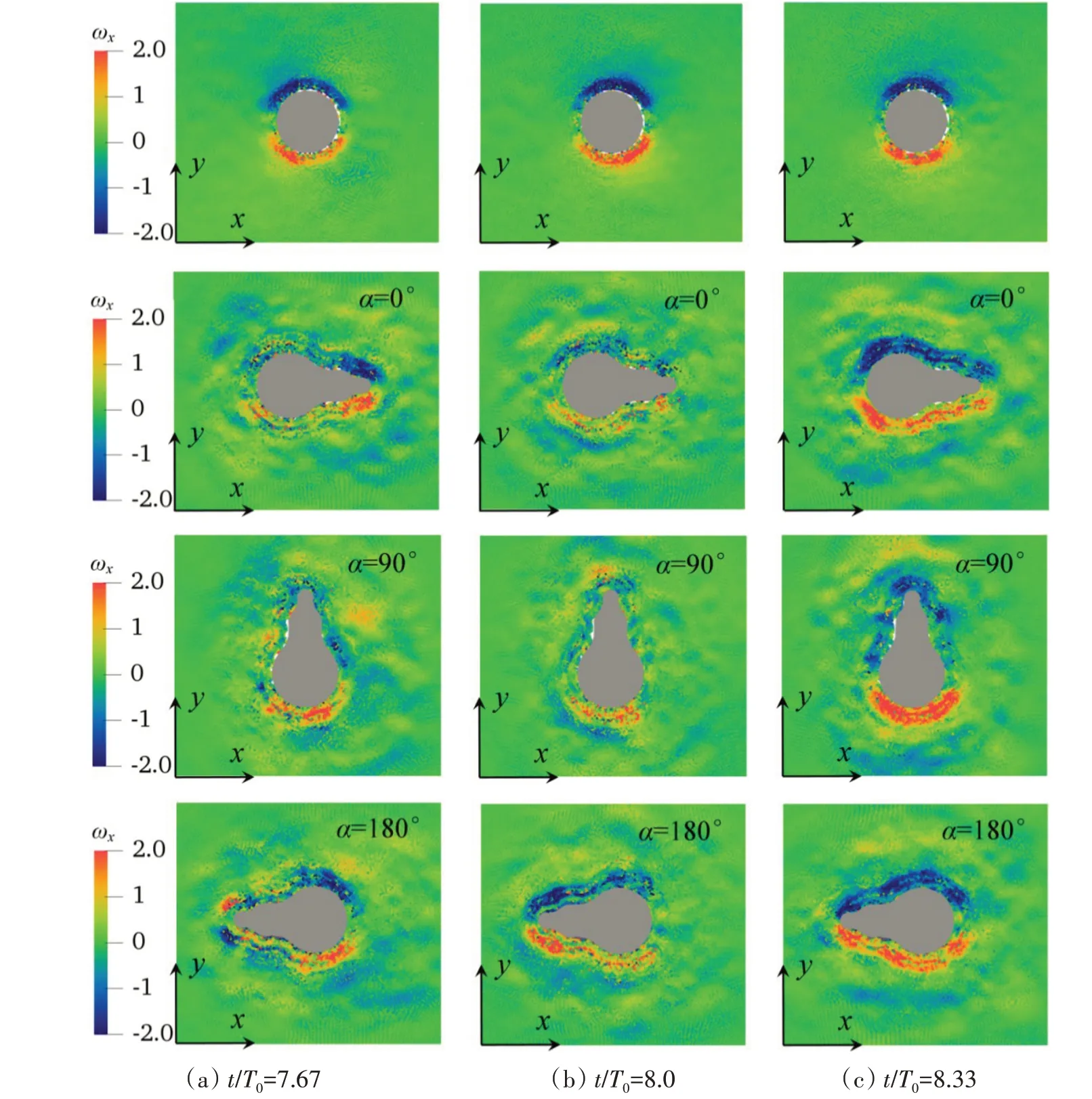
图11 不同旋转角度圆柱体与TPB结构在不同时刻的涡量分布Fig.11 Distribution of ωx for circular cylinder and TPB structure with different rotation angles at different times
在α=0°工况时,涡量分布区域随着波浪运动而逐渐变化,在波峰离开结构时(t/T0=8.33)涡量区域达到显著增大状态,如图11(c)所示。在波峰来临之前(t/T0=7.67),涡量的分布主要集中在结构壁面下游处,当波峰冲击时(t/T0=8.0),结构壁面周围涡量分布较弱。当旋转角度α=90°时,涡量主要集中在结构的横流向上下侧面附近,此时波浪对其的冲刷作用与α=0°工况结果相比较弱。这主要由于在α=90°工况时,波浪对结构冲击作用增大造成该区域的波能耗散较大,随后波浪沿着TPB 结构上下两侧传播并产生一定绕射现象从而促使此时的冲刷作用发生在固定区域,这与其流场波面速度分布特性相一致(见图10(d))。当旋转角度增加至α=180°时,波浪对其冲击作用的迎流面区域减少,此时其所受冲击作用减弱。值得注意的是,α=180°工况下TPB受波浪的冲刷作用显著地增强,因为其不同时刻上下两侧面附近处的涡量分布均较为强烈。事实上,结构壁面附近处较强的涡量分布会引起较大的吸力,这导致波浪对其造成较大的冲刷作用。
5.4 结构周围速度矢量分布
由于TPB结构的存在,波浪运动响应特性与水动力学特性发生变化,从而对TPB的受力特性造成影响。为了进一步揭示TPB 与波浪耦合作用机理,了解结构周围的速度分布是十分重要的。图12给出了三个不同时刻(t/T0=7.67、8.0、8.33)下在z=0.05 m 处TPB 结构周围的三维速度矢量分布并引入单圆柱体结果进行对比分析。从图中可以明显观察到单圆柱与TPB 结构周围存在强烈的三维流动效应。由于单圆柱体与TPB 结构在迎流面的阻挡作用以及在背流面的屏蔽效应,导致其迎流面和背流面处流体粒子的速度小于侧面处的速度,详细可见图12(c)。因此,在结构的侧面更可能发生波浪冲刷作用,相关文献[2]中也有类似的记载。值得注意的是,在t/T0=7.67 时刻(图12(a)),流体粒子以较大的顺流向速度冲击结构体迎流面;而在t/T0=7.67 时刻(图12(b)),具有较大速度的顺流向流体粒子在结构体的背流面中心线处汇集。

图12 圆柱体和TPB在z=0.05 m处不同时刻三维速度矢量分布Fig.12 3-D velocity vector distribution around the cylinder and TPB at different times at z=0.05 m
另外,TPB 结构在0°工况的速度矢量分布与单圆柱工况结果相类似,这与上一节中涡量的分析相类似,这直接导致两者所受波浪力的特性相近。而对于90°工况,由于其自身受波浪冲击作用的接触面积显著增大,造成其受波浪力脉动性显著增大,同时也可观察到波浪的冲刷作用主要发生在其上下侧边,这与流场图分布结果一致。当TPB结构旋转角度增加至180°时,受波浪冲击作用的迎流面接触面积显著减少,导致其受波浪力作用也大幅地减弱,而此时冲刷作用接触面显著增大进而导致其受冲刷作用显著增加。
综上可知,当TPB 结构旋转角度为0°时,波浪的冲击作用与冲刷作用均较强;当TPB 结构旋转角度为90°时,波浪对其的冲击作用较强而冲刷作用减弱;当旋转角度为180°时,波浪对其冲击作用较弱而冲刷作用显著增强。
5.5 不同数值水池参数对结构受力特性分析
本节主要分析针对旋转角度α=0°、90°、180°三个特殊工况下TPB 结构所受最大波浪力受相关参数的影响特性。图13 对不同数值水池波浪参数(波周期T、波高kH、水深kd)对TPB 结构所受最大波浪力的影响进行了统计分析,同样与单圆柱体相关结果进行了对比分析。最大波浪力随着波周期的增加而逐渐增大并在T=1.6 s 时达到峰值,随后逐渐缓慢地减少,如图13(a)所示。值得注意的是,单圆柱、TPB(α=0°)与TPB(α=180°)工况的最大波浪力在T=1.4~1.8 s 区间变化较为平缓,此区间被称为最大波浪力区间。另外,可以发现单圆柱体最大波浪力的变化趋势与TPB(α=0°)工况的结果基本一致,这种现象同样可在图12中观察到。而TPB(α=180°)工况的分布曲线基本位于其他工况结果下方,这与前面的流场涡量与速度矢量分析相一致。
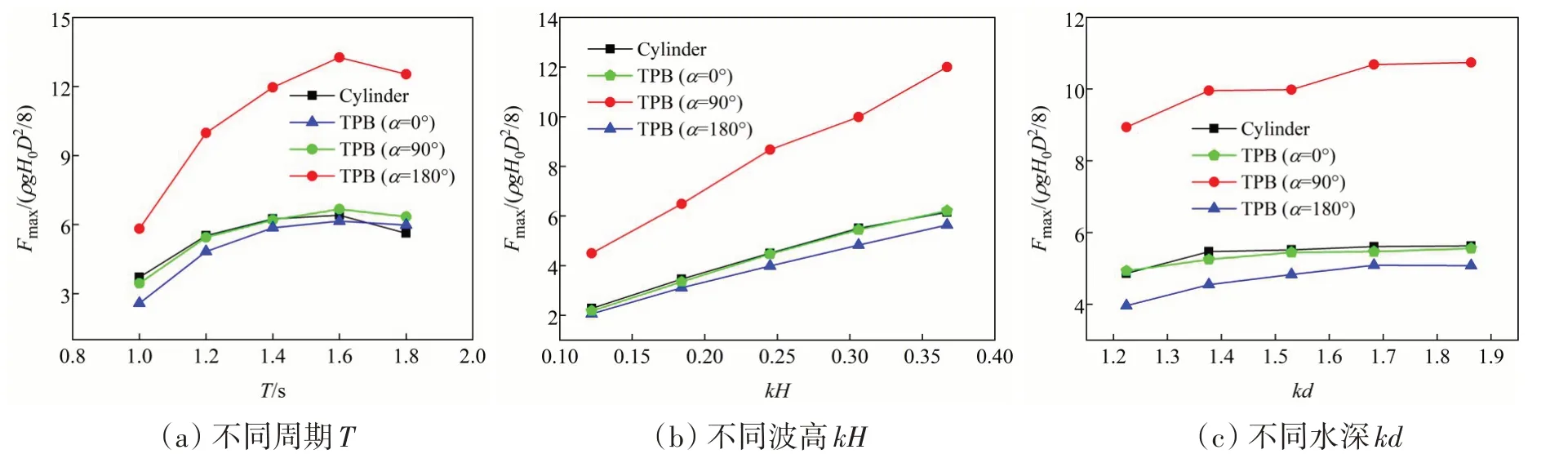
图13 不同参数对结构所受最大波浪力的影响Fig.13 Influence of different parameters on the maximum wave force on the TPB structure
从图13(b)可知,最大波浪力随波高变化基本呈现线性增大的趋势,因为入射波的波高越大波浪所具有的能量越大,对结构造成的冲击作用亦越强。值得注意的是,旋转角度为0°的TPB结构最大波浪力变化曲线与单圆柱相对应的曲线基本重合,这进一步说明了结构所受最大波浪力大小与其所受波浪冲击作用强弱直接相关,而结构所受冲刷作用对最大波浪力的影响较小。另外,最大波浪力随着水深的增加其变化趋势较为平缓,基本上在kd=1.38~1.84区间稳定,表明这种最大波浪力区间更为显著,如图13(c)所示。
为了更进一步分析不同波周期对结构受力特性的影响,图14 对不同工况的TPB 结构所受波浪力随波周期变化的时程曲线进行了对比分析。不同周期的波浪力时程曲线存在明显的相位差,且波周期为1.0 s工况的曲线脉动性明显小于其他工况结果。值得注意的是,波浪力时程变化曲线第一次出现峰值的时刻(t/T0≈5)在不同波周期工况下有较大的差别,且波周期越大的工况出现峰值的数值越大,峰值出现的位置也越延迟。事实上,T=1.6 s工况的波浪力时程曲线在t/T0=4.96处出现较大的峰值点,随后随模拟时间的增加,峰值点的位置最大下降了22%。这主要是由于柱体上游表面对波浪的运动具有阻碍作用以及柱体表面处的波浪传播方向发生改变形成反射波,进而耗散部分入射波能量。

图14 不同波周期下结构所受波浪力时程分布Fig.14 Distribution of time-history of wave force with different wave periods
对于TPB 结构,随着波周期的增大,在无量时间间隔4~12内,峰值点出现的频率却逐渐减少。在相同时间间隔内,T=1.0~1.8 s 工况的峰值点出现的次数从9 次减少至5 次。这表明在波周期T=1.0~1.8 s范围内,柱体所受波浪力的振荡频率随波周期的增加而减弱,从而可减少柱体的疲劳损耗。值得注意的是,单圆柱工况在T=1.8 s时的波浪力时程曲线的振荡频率及变化趋势与T=1.2 s工况结果相一致,如图14(a)所示。不同旋转角度下,TPB结构波浪力时程曲线变化趋势基本一致,但是在脉动性变化上存在一定差异,这与最大波浪力变化特性相一致。
6 结 论
本文基于SPH 方法建立了波浪数值水池,采用了活塞式运动造波板对Stokes 二阶规则波进行了模拟,并采用粘性消波方法实现了消波功能。对SPH 模拟结果与理论值、实验值的对比分析,发现结果吻合较好。然后,分析不同旋转角度(α)与不同波参数的波浪对TPB 结构受力特性的影响,得到的主要结论如下:
(1)SPH 方法能够准确地模拟三维Stokes二阶规则波的运动,通过对波浪数值水池的自由液面高度与Stokes理论解及实验结果的对比验证、波浪与结构相互作用力的验证,发现两者的吻合度较好。
(2)从结构周围的速度场分布特性可知,TPB结构的迎流面对流体粒子的运动具有一定的阻碍作用与屏蔽效应,同时在波浪与结构迎流面交界面处产生与入射波运动方向相反的反射波并对后续入射波产生一定影响。
(3)涡量主要沿着结构上下两侧对称分布,与单圆柱体结果相比,TPB 结构壁面周围涡量分布呈现一定的紊乱性。当旋转角度为0°与90°时,在相同时间内TPB结构壁面附近处涡量出现显著的增强趋势。当旋转角度为180°时,TPB 结构壁面附近处的涡量分布较为强烈。涡量分布较强的区域吸力较大,进而导致流体向结构表面处运动并发生冲刷作用。
(4)最大波浪力随着不同波参数呈现较大的差异性,其中,随着波周期与水深的增加,最大波浪力分布出现最大波浪力区间。随着波周期的增大,TPB 结构波浪力时程曲线的振荡频率逐渐增强,导致结构出现疲劳破坏。
