设计导向下的结构拓扑优化研究
2022-04-21周嘉侃夏利娟黄开艺
周嘉侃,夏利娟,黄开艺
(上海交通大学a.海洋工程国家重点实验室高新船舶与深海开发装备协同创新中心;b.电力传输与功率变换控制教育部重点实验室,上海 200240)
0 引 言
结构拓扑优化是工程结构设计的重要组成部分,具有效率高、灵活性高等特点。1988年,Bendsoe与Kikuchi 等[1]以引入微结构单元的理念首次提出了均匀化拓扑优化方法。在均匀化方法的基础上,Mlejnek等[2]提出了变密度方法,将设计变量转变为人为定义的伪密度参数,并通过伪密度的取值决定单元的删除或保留。变密度法常用的插值函数模型有SIMP 模型[3]与RAMP 模型[4],其中SIMP 模型基于各向同性微结构,以幂函数的形式建立伪密度与体积、刚度的关系。在拓扑优化的研究过程中,一些学者针对变密度法的材料插值函数进行改进[5-8],并对优化过程中存在的棋盘格效应、灰度单元等问题给出了解决方案[9-10]。结构拓扑优化在船舶设计中具有广泛的应用,刘宏亮等[11]使用生长进化拓扑优化算法进行了船舶中剖面横撑结构的优化;程远胜等[12]对肘板的拓扑形式进行了优化,降低了应力集中现象;张会新等[13]对船舶上层建筑板架进行拓扑优化,提高了板架的固有频率。
在实际生产中,对于结构的拓扑构型存在具体的设计需求,如船舶结构中因维护需要而设立的人孔,因装载与搬运便利而设立的大开孔,客机机舱地板梁预留铺设电缆与管道的空洞,因阻隔需要而设置的外突结构等。这些设计需求对结构力学属性的影响不可忽略,丁运来等[14]对船体结构中不同的开孔结构进行了研究,计算了孔边缘的应力分布。而拓扑优化的最终构型因不可控制而难以应用于实践,目前关于改善拓扑构型的相关研究主要集中于解决工程制造性、棋盘格效应等问题,如李伯豪等[15]提出了一种基于参数化水平集的后处理方法,提高了拓扑构型的可制造性;Boutdin 与Borrvall等[16-17]提出了密度过滤法,通过修正伪密度改善拓扑构型,处理棋盘格效应。尽管结构的设计需求十分重要,但以既定设计需求构型为导向的拓扑优化方法仍有待进一步研究。
基于此,本文通过构造基于单元灵敏度的修正函数,改进SIMP变密度法,建立设计导向下的结构拓扑优化模型。之后通过Python语言编程加以实现,使用短悬臂梁经典算例对模型进行可行性分析,最后对某油船货油舱板架结构进行设计导向下的拓扑优化。
1 SIMP法拓扑优化模型
1.1 优化算法思想
本文主要选取以体积为约束条件,结构刚度最大化的拓扑优化问题。首先使用有限元软件对连续体进行单元离散,赋予单元伪密度。选取最优准则法作为优化算法,通过库恩塔克条件建立优化准则并生成迭代格式,对单元伪密度进行迭代。迭代完成后,保留伪密度较大的单元,剔除伪密度较小的单元。
1.2 灵敏度计算与迭代公式
本文选取的SIMP拓扑优化模型可表述为

式中,V*为给定的体积约束,U为位移向量,K与Ki分别为总体刚度矩阵与单元刚度矩阵,Ki0为初始单元刚度矩阵,t为设计变量向量,p为权系数。根据文献[18],构造拉格朗日函数L(t):
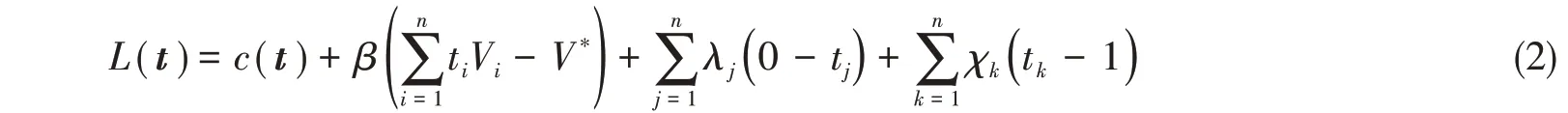
式中,β、λj、χk为拉格朗日乘子。由于迭代作用的伪密度介于上下界之间,可得λj=χk= 0,根据库恩塔克条件,

式中目标函数对设计变量的灵敏度可通过对有限元方程K(t)U(t)=F与式(1)中目标函数求导,并联立化简得到
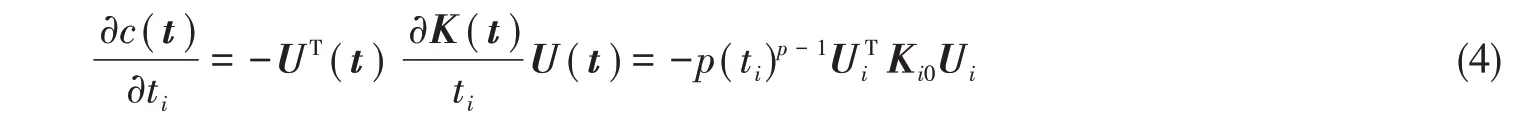
结合式(3)库恩塔克条件,可构造迭代因子:

式中拉格朗日乘子β可根据文献[19]的二分法计算,迭代公式如下所示:
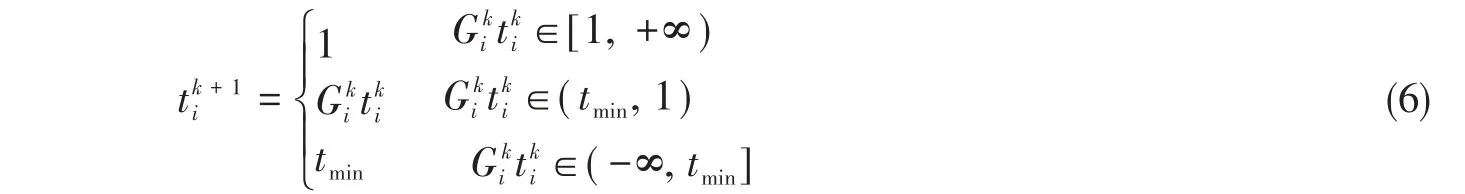
式中,tmin为避免刚度矩阵奇异而设置的最小伪密度。为保持迭代过程的稳定,引入移动极限常数δ和阻尼因子η,SIMP法迭代公式为

式中迭代参数的选取如表1所示:

表1 SIMP法迭代参数Tab.1 Iterative parameters of SIMP
1.3 灵敏度过滤与收敛准则
采用灵敏度过滤法处理棋盘格效应,对式(4)的灵敏度进行过滤:
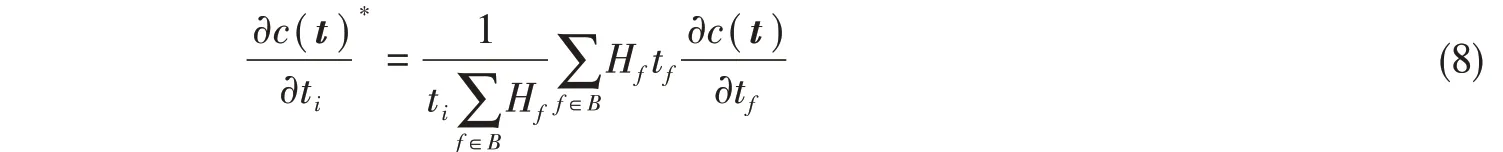
式中:∂c(t)*/∂ti为修正后单元i的灵敏度;∂c(t)/∂tf为修正前单元f的灵敏度;Hf=rmin-d(i,f),rmin为过滤半径,取为1.5倍的单元最小直径,d(i,f)表示单元i中心至单元f中心的距离;集合B表示所有与单元i距离小于rmin的单元集合,即{f|1 ≤f≤n,Hf>0} 。
采用两次迭代设计变量最大分量的相对误差作为收敛准则,同时加入最大迭代次数以保证优化迭代的终止:
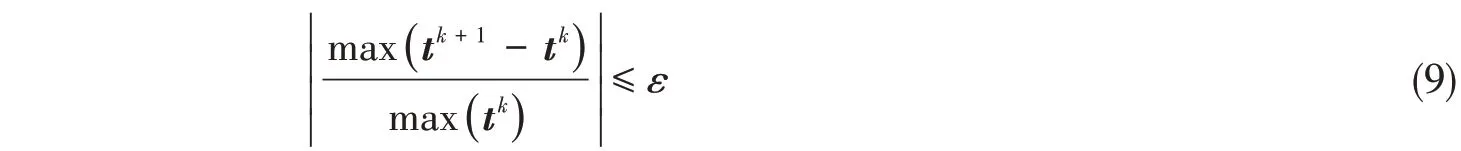
式中,ε取0.01,最大迭代次数取50,当迭代终止时,以0.5作为单元增删的临界密度。
2 设计导向下的拓扑优化模型
2.1 设计导向算法思想
对拓扑构型的需求可转化为控制设计区域内某些子域中单元的存在性,可通过修改迭代过程中对应单元的伪密度实现。如需子域A中的单元在拓扑优化的结果中存在,则在每一次迭代中,不断增加A中单元的伪密度,提升单元被保留的概率,反之亦然,最终达成拓扑优化迭代与设计导向之间的平衡点。
2.2 设计导向修正函数
本文使用设计导向修正函数Di控制迭代中单元密度的调整,使拓扑迭代向设计需求构型转变,修正方式如下:

式中,t为调整后的单元密度,tD为修正幅值,用于控制导向幅度的大小。设计需求导向修正函数Di需满足式(11),保证调整前后结构总体积的恒定:

当单元被均匀离散时,不同单元之间的体积差异可被忽略,可近似为= 0。
设需要调整的子域为M,作如下定义:若设计构型要求子域M中的单元存在,则称子域M为存在域,反之则称其为剔除域。表2列出了本文构造的设计导向修正函数的表达式。

表2 设计导向修正函数Tab.2 Design-oriented correction functions
表2 中,常数P用于满足式(11);Si为单元i的灵敏度;Sinc_max、Sinc_min、Sexc_max、Sexc_min分别为子域M内外的单元灵敏度最大与最小值,用于灵敏度归一化处理;正数q为形状因子,用于控制修正函数的形状,q越大表示修正函数对灵敏度的变化越敏感。
修正函数根据单元的灵敏度确定单次迭代中对单元伪密度修正的量。以剔除域M为例,为降低子域M中单元的伪密度,同时应尽可能减少因改变密度而导致的目标函数增加,修正函数采用如下策略进行单元伪密度调整:
(1)对于剔除域M内的单元,降低处于存在状态的单元密度,且单元灵敏度越低,调整幅度越大,反之亦然。
(2)对于剔除域M外的单元,增加处于删除状态的单元密度,且单元灵敏度越高,调整幅度越大,反之亦然。
2.3 设计导向下的拓扑优化流程及程序实现
通过上节构造的设计导向修正函数,在每一次迭代中,单元的伪密度将会被修正。具体的优化流程如图1所示,优化求解步骤如下:
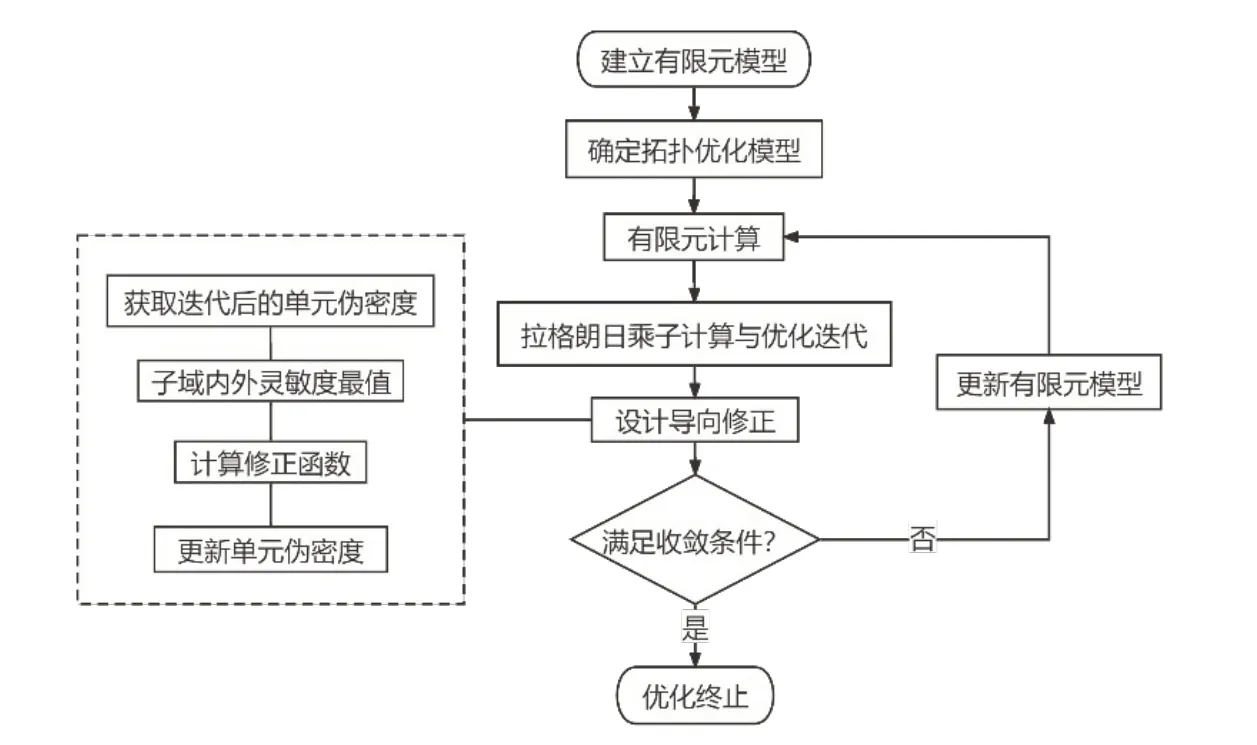
图1 设计导向下的拓扑优化流程Fig.1 Design-oriented topology optimization process
(1)建立有限元模型,定义设计区域、设计导向的子域等,施加边界条件与载荷。
(2)进行有限元分析计算,提取结果文件中各单元的刚度矩阵与位移向量。
(3)计算设计变量灵敏度,进行灵敏度过滤,计算迭代因子、拉格朗日乘子,代入迭代公式计算得到新的设计变量值。
2.5.2.2 农业防治首先进行合理轮作,不能和瓜类、向日葵、茄科等作物轮作,可以和禾本科、大豆、甜菜等轮作。其次是进行深耕秋翻,将种子翻入20cm以下土壤深处,可以减轻食葵列当种子的萌发。最后就是及时铲除列当,在列当开花结籽前,结合除草将列当铲除。
(4)统计子域内外的设计变量灵敏度最值,计算设计导向修正函数,再次更新设计变量。
(5)判别是否满足收敛条件,如未满足,则修改模型,返回步骤(2);如满足,则迭代结束,根据单元删除的临界密度获得对应拓扑构型。
本文使用Hypermesh建立有限元模型,并输入Nastran进行有限元计算,从计算结果文件中提取各个单元的刚度矩阵与位移向量,通过Python编程实现设计变量的更新,再根据所得的结果修改有限元模型,实现设计导向下的拓扑优化迭代过程。
3 算例及分析
3.1 短悬臂梁算例
如图2所示,悬臂梁左端固支约束,右边缘中点受竖直向下方向的集中载荷作用,梁的长度为200 mm,宽度为100 mm,集中载荷大小为1000 N。划分网格为40×20,材料弹性模量为206 000 MPa,泊松比为0.3,优化体积分数为0.5。
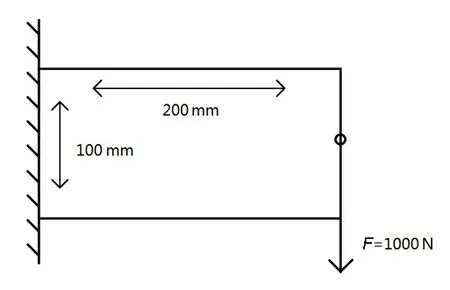
图2 短悬臂梁Fig.2 Short cantilever beam
图3 为无设计导向下的拓扑优化结果,优化后柔顺度为333.745 N·m,将优化构型的桁架根部设置为剔除域。选取“导向比”评价设计导向的效果,其定义为设计子域内达成导向的单元数与子域单元总数之比,如图3的导向比为3/16;选取“柔顺比”评价优化后的力学性能,定义为设计导向介入与不介入的柔顺度之比。导向比越高,柔顺比越低,表示设计导向效果越好。选取不同参数对短悬臂梁进行设计导向下的拓扑优化,得到表3与表4所示的结果。
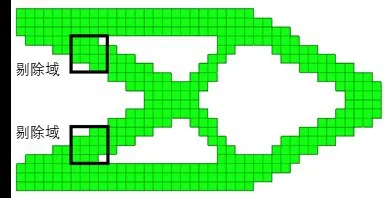
图3 无设计导向下的拓扑优化结果Fig.3 Topology optimization result without design guidance

表3 不同设计导向参数下短悬臂梁优化结果构型Tab.3 Optimal configurations of short cantilever beam with different parameters
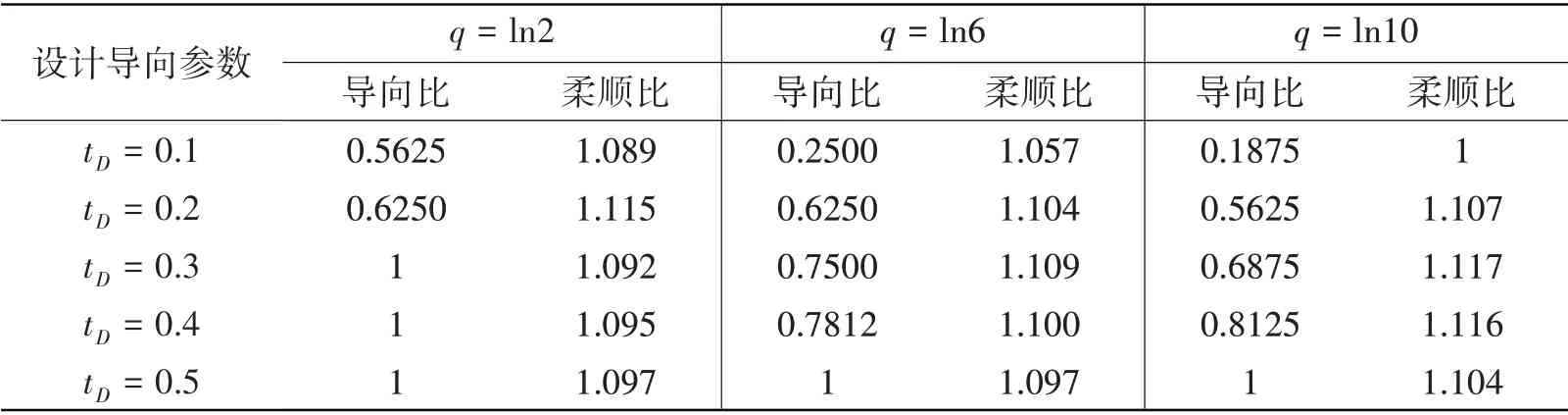
表4 不同设计导向参数下短悬臂梁优化数据Tab.4 Optimization data of short cantilever beam with different parameters
3.2 油船板架算例
图4(a)为一艘320 000 DWT 油船中部货油舱有限元舱段计算模型。如图4(b)所示,优化区域位于横舱壁相邻肋位,包含船底肋板与舭肘板。由于肋板靠近横舱壁,因此仅考虑图5 所示的4 种横向极限载荷工况,各工况的权重系数根据单工况下结构应变能大小确定。图6(a)为无设计导向下的拓扑优化构型,在横向载荷工况下,船底肋板由于承载来自海水与货物的压力,应力分布集中,单元倾向于被保留。在船底肋板处设置剔除域,使用设计导向下的拓扑优化算法进行优化。根据短悬臂梁算例结果,形状因子选取ln6,修正幅值选取0.4,得到优化后的构型如图6(b)所示,优化数据如表5所示。
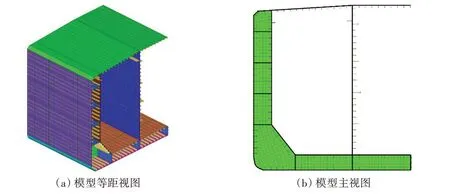
图4 油船有限元舱段模型Fig.4 Finite element model of oil tanker cabin

图5 油船舱段载荷工况Fig.5 Load conditions of oil tanker cabin
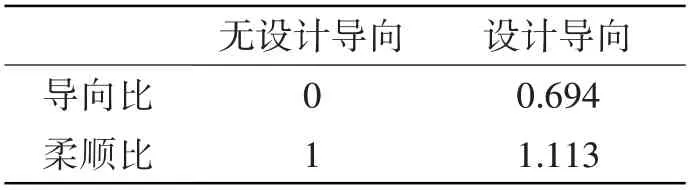
表5 油船板架优化数据Tab.5 Optimization data of oil tanker frames
图6(a)中,无设计导向的拓扑优化构型中船底肋板采用全封闭式,未考虑因检修或维护需要而设置的人孔。图6(b)中,随着设计导向的介入,船底肋板出现开孔,而舭肘板处开孔减小,可说明在船底肋板开孔的同时需要加固舭肘板。算例导向后的柔顺比小于1.2,表明设计导向下的拓扑优化模型能够结合开孔的设计需求,得到更加合理的拓扑构型以指导设计,进一步体现模型的可行性与稳定性。通过对比不同拓扑优化结果,综合考虑柔顺度、结构重量、导向比等指标,进行重新设计,得到新的结构拓扑形式如图6(c)所示。
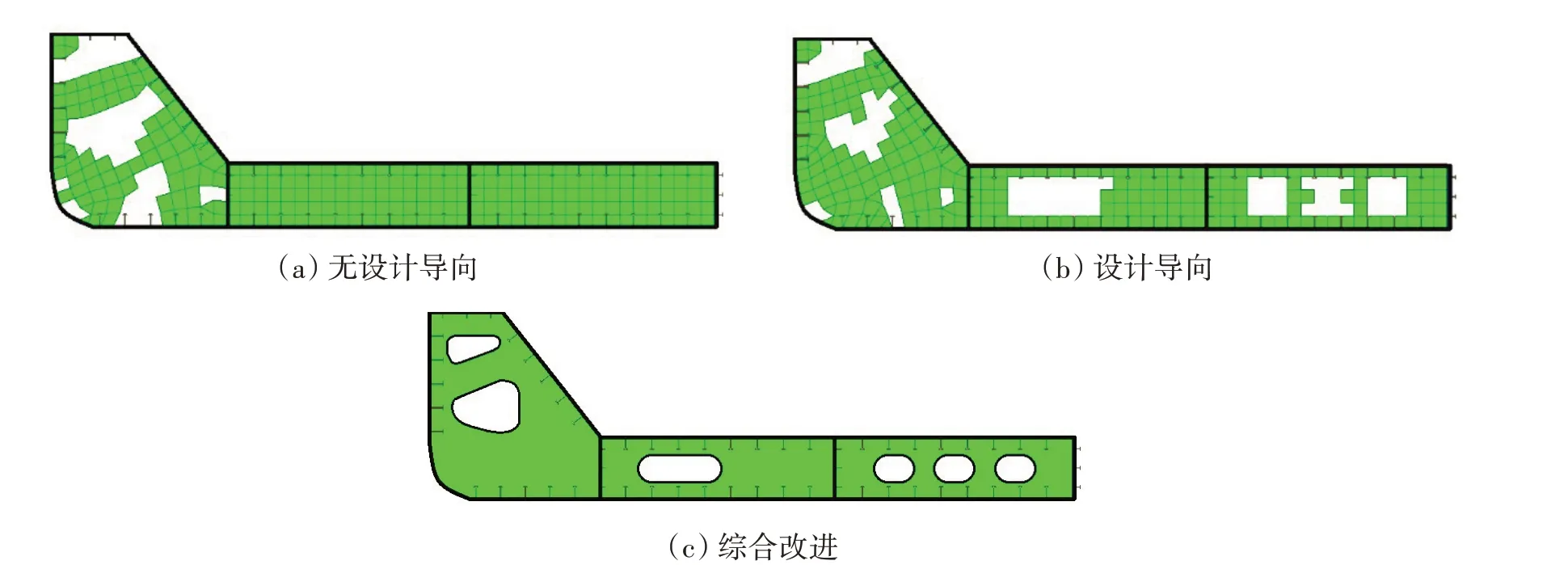
图6 油船板架优化结果构型Fig.6 Optimal configurations of oil tanker frames
4 结 论
本文通过构造修正函数,将其引入SIMP 变密度拓扑优化算法,建立了设计导向下的结构拓扑优化模型。采用以单元灵敏度为依据的修正函数,尽可能保留结构的力学性能,实现了拓扑构型向设计需求方向引导,并通过算例验证了模型的可行性和稳定性。数值计算可以得到如下结论:
(1)在拓扑优化程序中引入设计导向流程能够在维持一定柔顺比的情况下,获得较高导向比的拓扑构型,因此采用单元伪密度修正方法是可行的。
(2)模型参数的选取十分重要,过大的形状因子会导致柔顺比上升。对于本文算例,修正幅值选取介于0.3至0.4,形状因子选取介于ln2至ln6可获得稳定、导向合理的构型。
(3)设计导向下的拓扑优化模型在求解过程中能够自发地进行材料优化配置,可为实际工程结构的优化设计提供参考方案。
