极限海况下动力定位船舶推力分配推进器饱和协议

刘大辉，赵 亮，徐胜文，陈 昱

（1.浙江大学建筑工程学院，杭州310058；2.中集海洋工程研究院有限公司，山东 烟台 264670；3.上海交通大学海洋工程国家重点实验室，上海 200240）

0 引 言

随着海洋勘探和开发逐步进入深海，动力定位系统已越来越多地应用于海上作业，例如电缆和管道铺设、海上油气钻探和潜水支持等[1]。由于深远海海况复杂，加之近年来全球气候变化，各种极端天气时常发生，如何保障生产与作业安全，这是以动力定位船舶为基础的海洋油气工业、海底管道铺设和潜水支持等领域亟需解决的问题。面对较高且变化剧烈的海况，传统的动力定位船舶推力分配策略较难完全满足安全作业的要求。

动力定位系统旨在通过自身的推进系统来调节船舶的水平位置和航向[2]。推力分配策略作为动力定位船舶控制指令的具体执行方法，其职责是产生合适的推力及力矩以抵抗环境载荷干扰，使船舶达到给定平衡位置与艏向。若推进系统由于自身限制或发生故障不能正常工作，致使推进效果不及预期，将直接影响船舶的定位能力。为尽可能减小这种影响，动力定位船舶配备的推进器一般多于3个，形成过驱动推进系统以保证自身长期工作的安全性与可靠性[3]。过驱动推进系统有助于船舶获得更高的操纵性和可靠性，但同时推进器数量的增加也给推力分配带来了不少挑战。

对于动力定位控制器给定的要求推力，过驱动推进系统存在多个不同推力大小和方向的组合与之匹配，但实际只需要一个组合推力。此时推力分配问题可以看作是一个以满足给定控制力为前提，以推进器本身推力范围及变化率、转角范围及变化率以及水动力干扰等条件为约束，寻找达到推进器能量消耗最小或其它目标的一个组合优化问题[4-6]。Harkegard[7]提出了实时求解约束优化问题的方法；Xu等[8]提出了一种动态的禁止角跨越策略，可以为全回转推进器提供一个更可行的转角区域；Fossen等[9-10]对现有的推力分配策略进行了详细的分类和分析；Ruth[11]总结了有关动力定位系统推力分配方面的现有文献。

文献中对于极限海况下动力定位船舶推力分配策略的研究极少。Arditti 等[12]提出了一种推进器饱和协议，处理出现多个推进器推力饱和的情形，允许推进器分配的推力与控制系统所需的控制力存在适当的偏差，当推进器无法产生所需的推力时，可以使推进器逐个饱和，但是这种方法不能保证分配结果的全局最优化。

本文提出一个推进器饱和协议使各推进器的性能充分发挥，以更准确地提供控制器要求的推力。推力分配算法采用具有高鲁棒性的二次规划方法[13]。环境载荷的估算基于经验公式、水动力计算或模型试验[14]。最后以某半潜式平台为研究对象，在传统和优化后的推力分配策略下分别进行时域仿真验证提出的饱和协议的有效性和优越性。

1 推力分配逻辑

1.1 坐标系

动力定位船舶的随船坐标系坐标原点取在平台的重心O，X轴正向沿船长指向船艏；Y轴正向沿船宽指向左舷；Z轴与XOY平面垂直，方向竖直向上。由于计算时需要考虑平台三个自由度上的运动，也即考虑平台的纵荡、横荡和艏摇运动。规定平动状态沿坐标轴的正向为正，转动状态满足右手定则以绕Z轴逆时针为正，环境力的角度从船尾起逆时针为正。船舶坐标系的选取如图1所示。

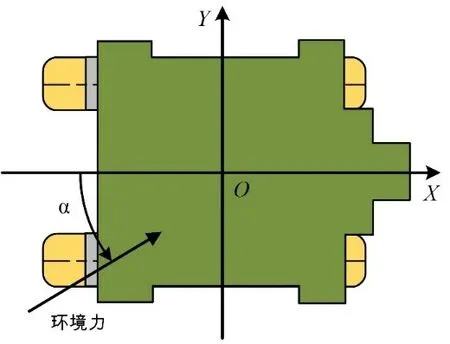
图1 动力定位船舶坐标系Fig.1 Coordinates of the DP vessel

1.2 推力分配数学模型

推力分配的目标是使推进系统以最小的能量消耗提供控制器要求的推力，约束条件为推进器的自身物理限制[15-16]。推力分配问题可视为在约束条件下寻找满足目标分配组合的最优化问题。通过最优化方法，可以在多个目标组合中寻找最优组合。但是在极限海况下，由于环境载荷较大且变化较为剧烈，所以对推力分配算法要求能够快速地分配出可靠的结果。文献中有很多关于最优化的方法，其中二次规划方法被证明是相对有效和鲁棒的。因此，本文中采用二次规划方法来求解推力分配问题。

若一个船舶装备有m个推进器，推力系统产生的推力向量τ∈R可以表述为

式中，τX是纵荡力，τY是横荡力，τN是艏摇力矩。向量u∈Rm包含每个推进器沿船艏和左舷方向产生的推力。推进器配置矩阵B∈R3×m的i列可以表示为

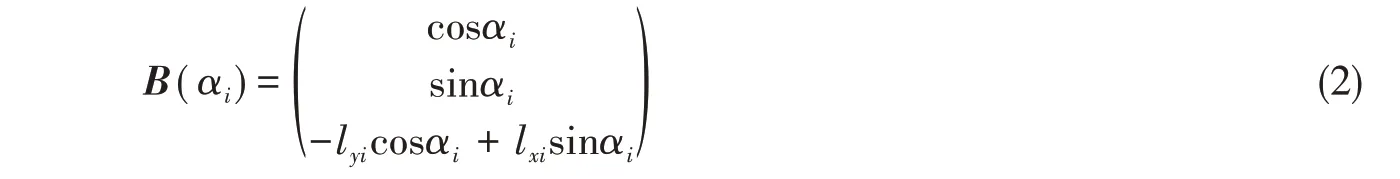
第i个推进器在水平面的位置用(lxi,lyi)表示。

Johansen等[15]针对带有全回转推进器的推力分配问题，提出了准动态最优化模型，为了便于求解，将其进行线性化处理。

目标函数：

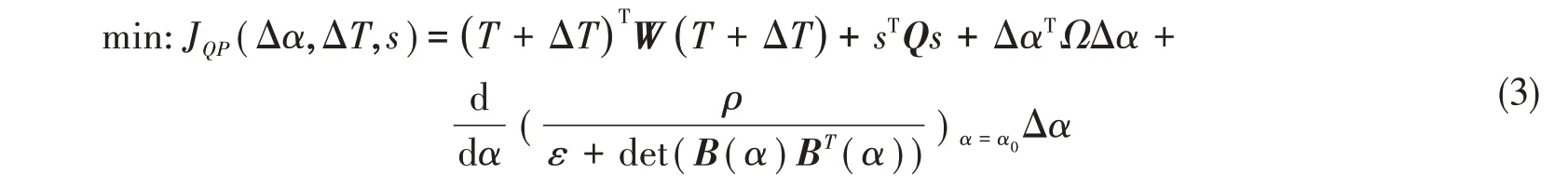
约束条件：

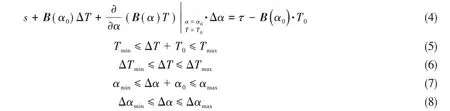
该优化问题使用凸二次规划方法进行求解。目标函数第一项表示总推力消耗，W是一个正定对角矩阵，表示各推进器的权重系数。第二项为要求推力与分配力的误差，Q为误差权重矩阵。第三项要求推进器的转角变化率尽可能小，以减小磨损。最后一项是奇异避免项，在目标函数中加入奇异结构惩罚项以避免奇异性的产生，其中( )ε,ρ＞0。等式约束（4）表示各推进器产生的推力应等于所需推力。不等式约束（5）～（8）代表每一时间步长内对推进器推力变化和转角变化的物理限制。

2 推进器饱和协议

由于全回转推进器受限于上述不等式的约束，导致推进器在一定的时间内所能旋转的角度、推力大小的变化都在一个范围内，如图2 所示。图中ΔT+、ΔT-表示T0在下一时刻所允许增量的最大值和最小值，表示为

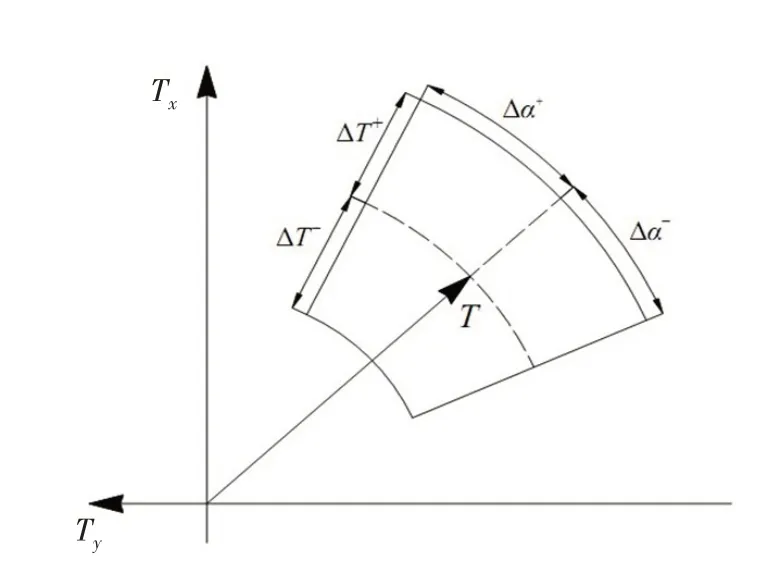
图2 全回转推进器推力动态变化区间Fig.2 Thrust dynamic range of the azimuth thruster

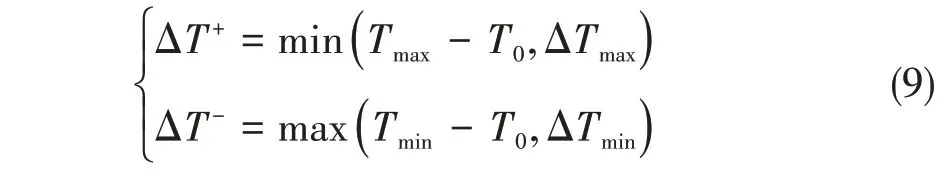
式中，ΔT+、ΔT-受到Tmax、Tmin、ΔTmax、ΔTmin的共同限制。其中ΔTmax、ΔTmin的选定兼顾桨叶、轴承磨损以及电机功率，通常在进行动力定位作业前预设为定值。

当推进系统的工作海况由正常海况剧烈变化到极限工作海况，即所需推力剧烈增加时，可根据推力分配模型及二次规划求解得到分配结果，观察到某个推进器推力最先达到推力最大值，处于饱和状态即ΔT+=0，而其余推进器仍有推力余量。倘若海况持续增加，则到达饱和状态的推进器逐渐增多。如果推进系统没能快速达到最终的“平衡状态”将致使定位效果变差，并对后续定位产生影响。

在极限工作海况下，由于推进器推力最大值Tmax为实际物理值，为了能快速合理地分配出推力解，到达“平衡状态”，需要对推力分配结果进行监督，并对Δα、ΔT进行动态调整，尽量发挥推进系统性能。而本文对Tmax、Δα、ΔT在上述基础上再进行二次调整，为此设计了极限工作海况下的推进器饱和协议，实施流程如图3所示。

图3中，α0、T0为上个时刻推力分配的转角、推力，τ为t时刻待分配的控制力，通过二次规划求解，得到t时刻的α0、T0，然后进入下一时刻的推力分配，这是正常工作海况下的推力分配策略。在极限工作海况下，如果两个及以上的推进器出现饱和状态，对原始的变化量Δα0、ΔT0进行放松，可以得到新的变化量Δα1=η1Δα0，ΔT1=γ1ΔT0，其中η1(η1＞1)，γ1(γ1＞1)根据推进器的额定功率确定。然后在新的约束条件下再次执行推力分配，以上是传统的推力分配策略。在极限工作海况下，为了更充分地考虑推进器的饱和，本文提出一个饱和协议。

图3 极限海况下使用饱和协议优化的推力分配策略Fig.3 Thrust distribution strategy optimized using saturation protocol under extreme sea conditions

饱和协议中第一步要进行饱和判定，即若存在第j个推力值T(j)=Tmax0，且个数大于或等于2个，则执行饱和协议。第二步将ΔT0、Δα0进一步放大，得到ΔT=γ1γ2ΔT0，Δα=η1η2Δα0，其中η2(η2＞1)，γ2(γ2＞1)根据经验设定，不宜取得过大。同时为得到推力分配的最优解以及后续饱和判定，对Tmax0同步进行放大，得到Tmax=β·Tmax0。β的初始值选为β1，且1 ＜β＜β1。对以上约束条件进行更新完毕后，进行再次推力分配求解。第二步对求解的推力进行再次饱和判定，如果仍有两个或以上的推进器饱和，则直接跳出循环。若饱和推进器个数减少，则只对β进行更新以减小β取值，获得新的Tmax，参与下个循环的推力分配求解。以此类推，直到出现分配的推进器有两个达到饱和状态，此时保存上一步的推力分配结果作为最终解并跳出循环。最后为了符合推进器推力的实际物理限制，将最终解的T和α按照ΔT1、Δα1为边界进行截断，得到饱和协议下的最终解。执行此饱和协议的关键是使推进器的约束条件放宽，得到全局最优化的推力组合解，然后将超出最大推力物理限制的推进器产生的推力缩减到其实际约束条件的边界上，最大化地利用了各个推进器的性能。

3 算例和结果

3.1 算例概览

对于提出的极限工作海况下的推力分配策略采用自主开发的程序[16-17]进行时域仿真。选用一艘装备8 台全回转推进器的半潜式平台作为研究对象。半潜式平台的关键参数如表1 所示。所有全回转推进器具有相同的参数，其物理特性参数见表2。推进器的布置如图4 所示，推进器位置坐标见表3。推进器间的水动力干扰忽略不计，即不作禁止角处理。推进器工况为全部正常工作，风、流载荷在此忽略不计，只考虑波浪载荷。表2 中推力增量ΔT0= 30 kN/s，Tmax0= 800 kN，Δα0= 2°/s，考虑推进器电机的额定功率，取η1= 1.5，η2= 1.2，γ1= 1.5，γ2= 1.2，β1= 1.5，即Δα1= 3°/s，Δα2= 3.6°/s，ΔT1= 45 kN/s，ΔT2=54 kN/s。

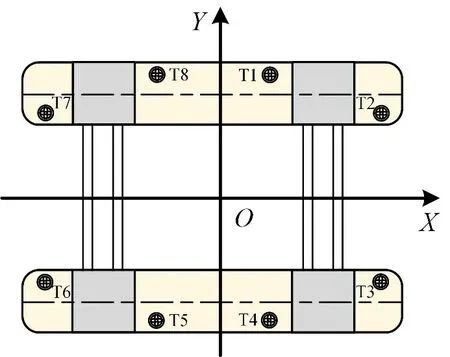
图4 推进器布置示意图Fig.4 Diagram of thruster configuration

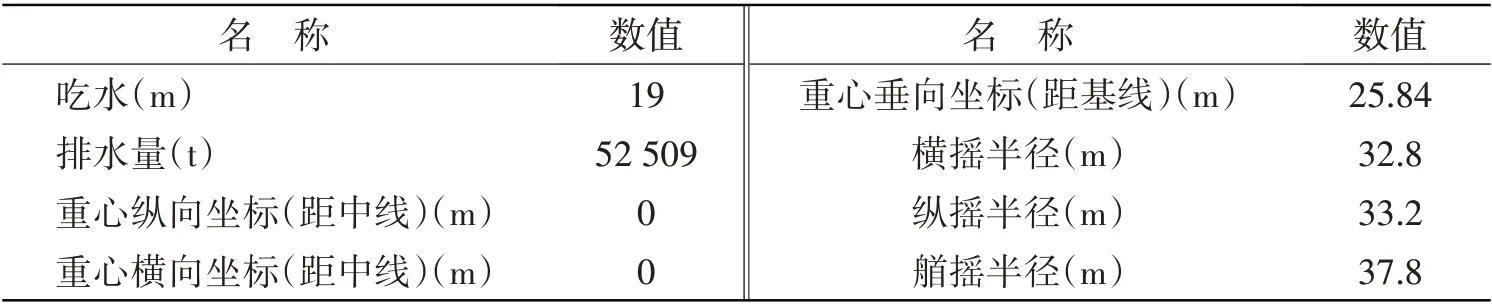
表1 半潜式平台关键参数Tab.1 Main parameters of semi-submersible platform

表2 推进器物理特性参数Tab.2 Physical characteristics of propeller

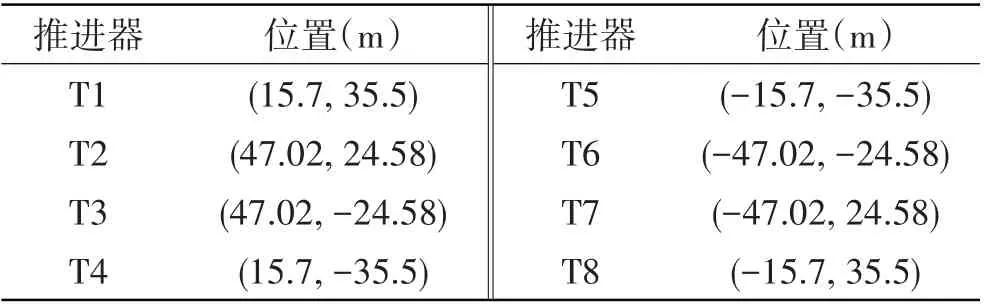
表3 推进器的位置Tab.3 Thruster locations

3.2 时域模拟仿真结果

从图5可以观察到，对剧烈变化的待分配控制力，采用提出的饱和协议的推力分配算法相较于传统推力分配算法能够更准确地给出分配结果。极限工作海况开始于红色区域。红色区域内，待分配的推力急剧增加，采用饱和协议优化的推力分配结果得到的纵荡、横荡方向上的推力明显大于传统推力分配策略的相应推力，而艏摇方向上的力矩略小于传统推力分配结果，但仍能满足平台艏摇方向的定位要求。红色区域之后两种策略虽均能较好地满足待分配控制力，但在某些时刻采用提出的饱和协议的推力分配结果明显优于传统策略结果，这表明执行了饱和协议的推力分配策略使推进系统更准确地满足所需的控制推力。

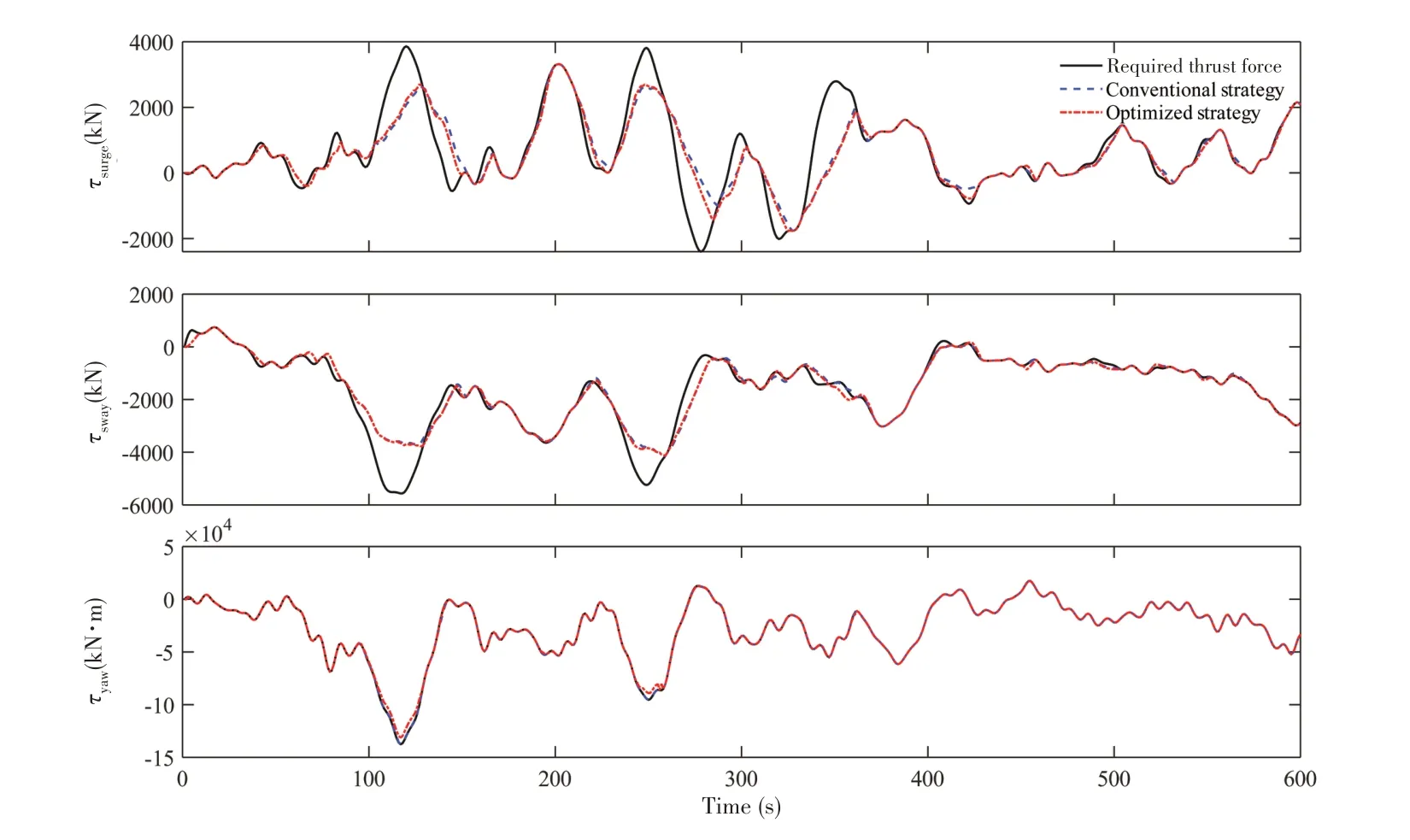
图5 使用优化与传统推力分配策略的推力时程Fig.5 Time series of thrust using optimized and traditional thrust allocation strategies

在图6～7 中，观察各推进器转角的时程变化，红色区域之前两种策略的转角几乎完全相同，此时并未激活饱和协议。在红色区域内，一旦执行饱和协议，一些推进器的转角出现略微变化，由于饱和协议并未更改对转角的约束，说明执行饱和协议时，推力变化也影响着转角。红色区域之后个别推进器转角发生变化，但转角变化趋势并未发生较大改变。因此，红色区域后优化后策略与传统策略的分配结果在转角上的差异可能是由于红色区域执行饱和协议带来的影响。

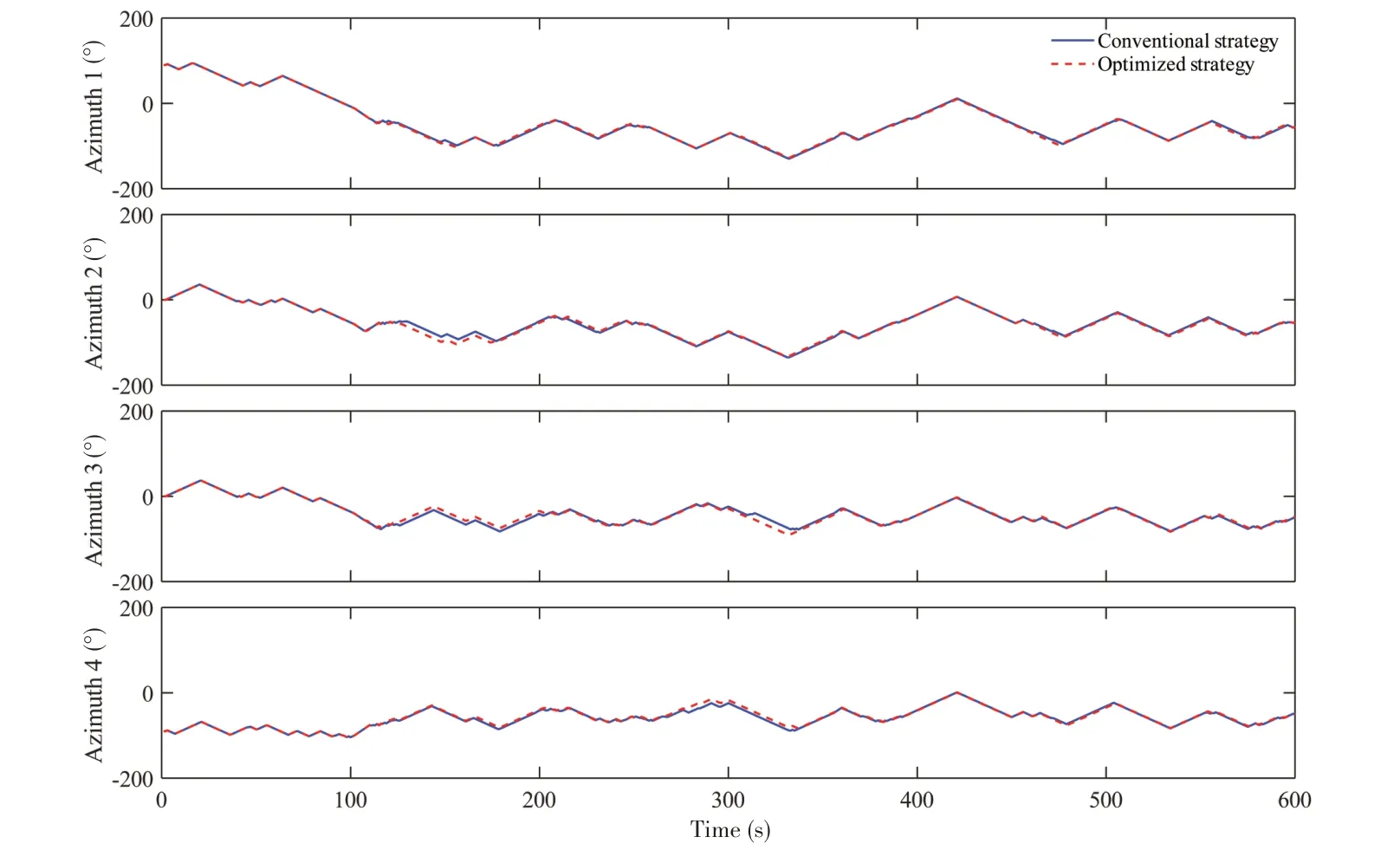
图6 使用优化与传统推力分配策略的推进器1～4转角时程Fig.6 Time series of Thruster Nos.1-4 rotation angle using optimized and traditional thrust allocation strategies

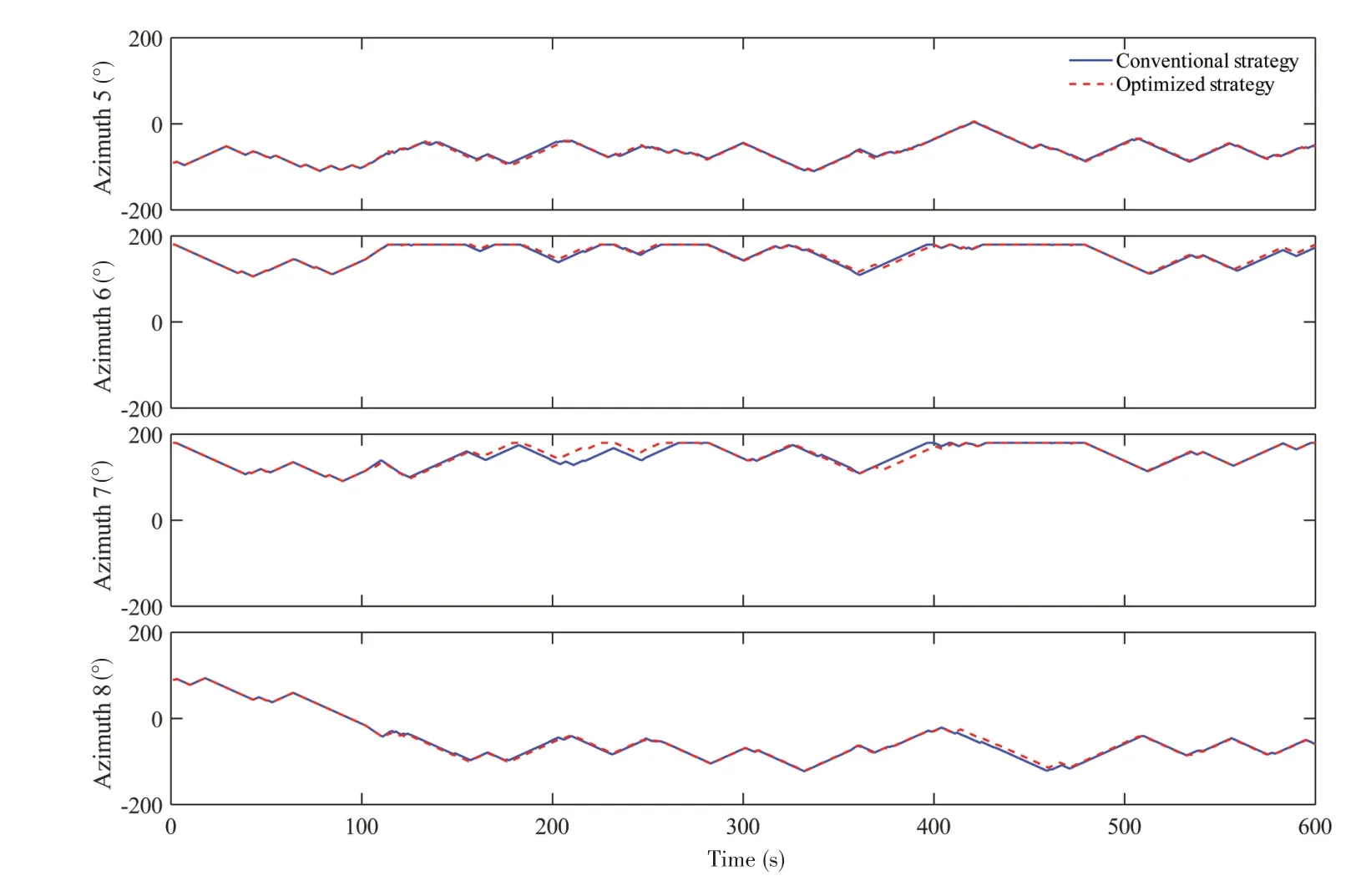
图7 使用优化与传统推力分配策略的推进器5～8转角时程Fig.7 Time series of Thruster Nos.5-8 rotation angle using optimized and traditional thrust allocation strategies

在图8～9 中，观察各推进器推力的时程变化，在红色区域内，由于推进器4、5 的推力达到饱和状态，以此激活饱和协议，在此期间有多个推进器的推力变化量呈增加趋势，相对于传统分配策略更早更快地达到了饱和状态，由图5红色区域的分配效果可见是有益的。红色区域之后，采用饱和协议推力分配的推力变化与传统策略结果相比仍有较大差异。

图8 使用优化与传统推力分配策略的推进器1～4推力时程Fig.8 Time series of Thruster Nos.1-4 thrust using optimized and traditional thrust allocation strategies

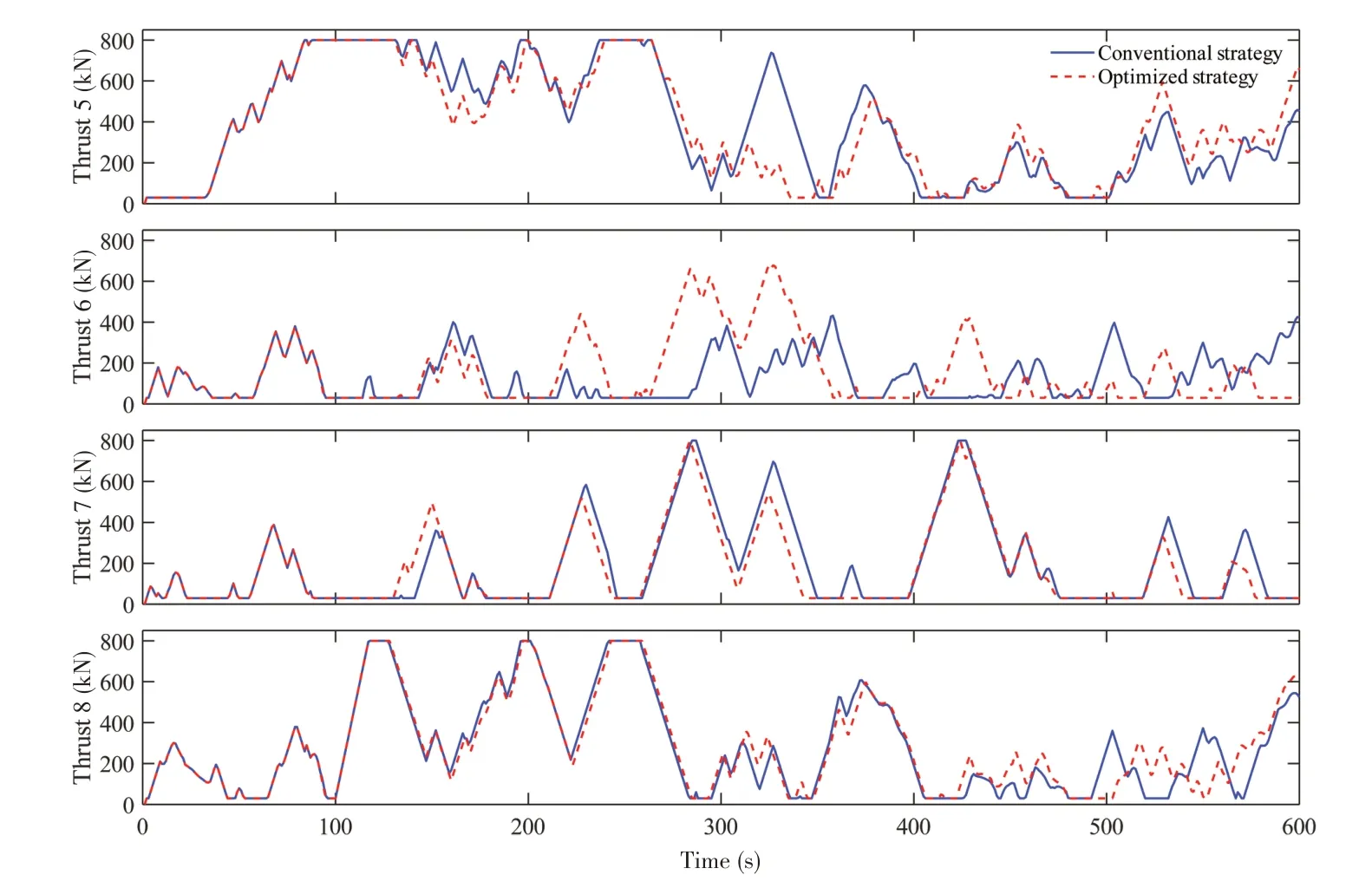
图9 使用优化与传统推力分配策略的各推进器5～8推力时程Fig.9 Time series of Thruster Nos.5-8 thrust using optimized and traditional thrust allocation strategies

从图10可以看出，采用优化与传统推力分配策略的动力定位系统功率消耗差别不大。在红色区域内，开始执行饱和协议，两种策略下的功率消耗差别并不明显。红色区域后一段时间内出现优化策略下的功率消耗大于或小于传统策略下的功率消耗情形，这是由于受到前面红色区域优化策略的影响，使得后续序列二次规划的初始条件发生改变，导致优化策略与传统策略分配的推力产生差别，进而造成了功率消耗的差异，但总体功率消耗差别并不明显。

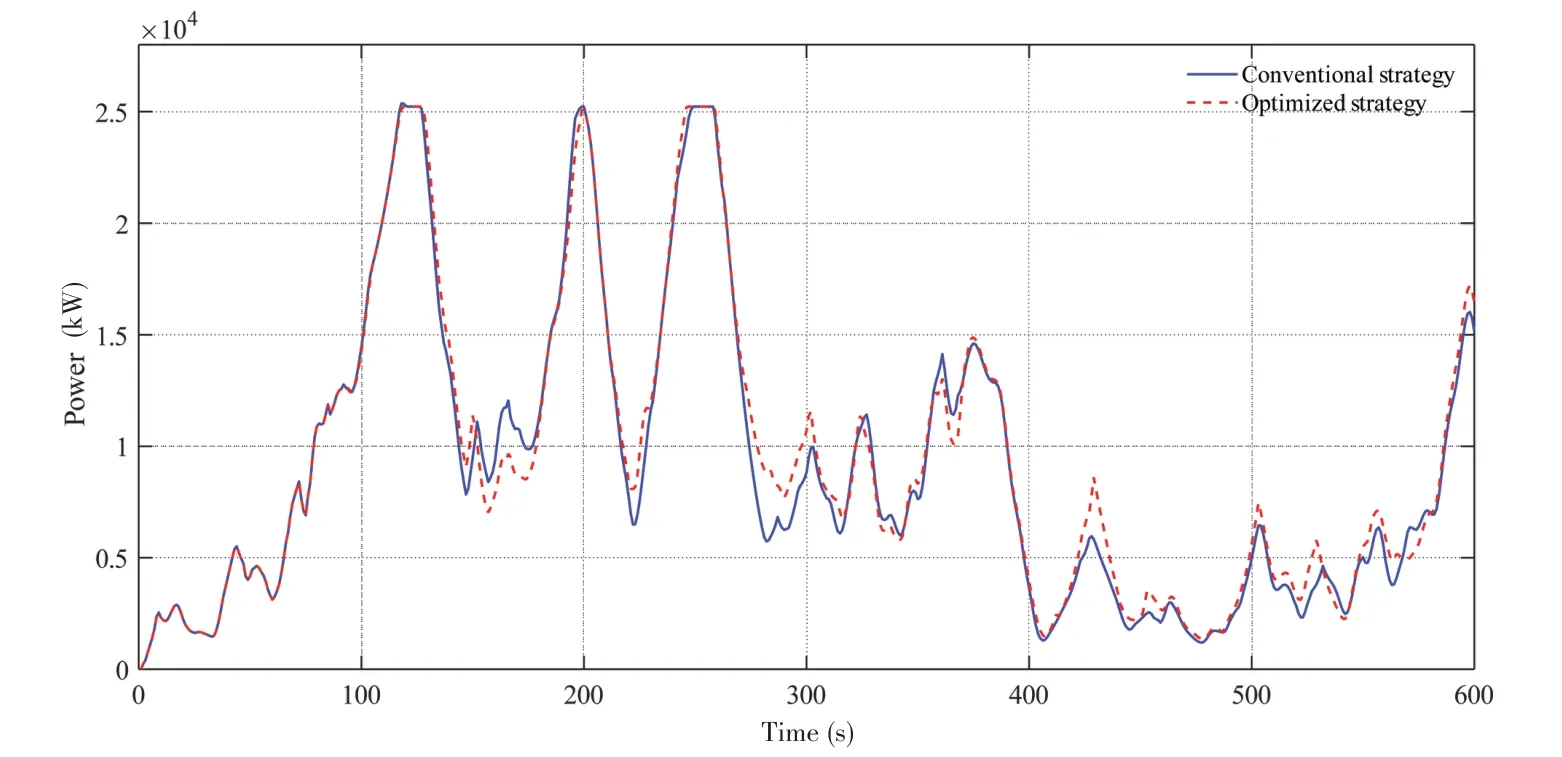
图10 使用优化与传统推力分配策略的总功率消耗时程Fig.10 Time series of total consumed thruster power using optimized and traditional thrust allocation strategies

4 结 语

针对极限海况下动力定位船舶可能面临多个推进器同时出现饱和的情形，本文提出了一个饱和协议用于推力分配策略。通过自主开发的动力定位时域程序对一艘装备有8台全回转推进器的半潜式平台进行了仿真模拟，对比了优化策略与传统策略下的推力分配结果，验证了优化策略的有效性和优越性。本文提出的极限海况下动力定位船舶的推力分配策略，在执行饱和协议时适当放松推力最大值限制，并进行二次推力分配求解，使其他未饱和推进器推力发挥更大作用，提高了推进系统应对剧烈变化控制力的反应速度，并分配出了更接近所需控制力的结果，对提高动力定位船舶在恶劣海况下的定位性能具有重要意义。