基于多重得分函数的知识嵌入模型

陈新元,谢晟祎,陈庆强,刘 羽

(1.福州工商学院工学院，福建 福州 350715；2.福建农业职业技术学院实验实训中心，福建 福州 350181；3.福建工程学院信息科学与工程学院，福建 福州 350118；4.福州墨尔本理工职业学院现代教育技术中心，福建 福州 350121)

0 引言

知识库(knowledge base, KB)是结构化的事实集合，常常以三元组的形式编码事实，三元组由头/尾实体和关系组成。主流知识库如NELL[1]，YAGO[2]和Freebase[3]等，在搜索引擎[4]、问题解答[5-6]和社交网络分析等领域[7]得到广泛应用。

KB中存在大量缺失事实，即三元组不完整，知识图谱补全(knowledge graph completion)[8-9]旨在解决该问题。链路/关系预测是知识补全的重要手段，通过提取潜在特征[10]或路径语义[11-12]，用已知信息生成新的有效事实；嵌入方法可以有效降低参数规模，经典模型如TransE[13]和DistMult[14]等，其中TransE将实体和关系映射为潜在特征的向量表达和向量间的距离/平移。此外也有研究尝试集成逻辑规则[15]，或利用卷积神经网络(CNN)辅助实体/关系的表示学习[16]，或使用循环神经网络(RNN)及其改进框架如LSTM，借助实体对的不同关系路径所携带的语义信息判定三元组的有效性[17-19]，或集成时序信息建模三元组[20]，或设计评分函数自由度更高的模型ConvKB[21]等。

然而，主流的嵌入模型大多使用单一得分函数学习多种关系模式，存在局限性，如TransE在处理对称关系模式时表现欠佳，嵌入表示在学习过程中趋近零向量；也有模型在处理反对称模式、组合模式或自反模式时发生性能下降。

因此本文在前人研究基础上，设计基于平移/旋转的MSF嵌入模型(embedding model with multiple scoring functions)，解决单一函数难以映射多种关系模式的问题。论文主要工作如下：1)设计基于多重得分函数的神经网络嵌入模型，实现多种关系模式信息的集成，在统一的训练框架下为不同的得分函数训练多组独立的嵌入向量表达；2)理论推导MSF可学习对称、反对称、反向、组合、自反等多种关系模式；3)使用基于阈值限制的损失函数(limit based loss function, LBLF)改善模型的泛化能力；4)在4个主流数据集WN18、WN18RR、FB15k和FB15k-237上，比较MSF模型和其他主流模型的性能表现，以及不同得分函数对整体模型的影响。

本文后续结构如下，第1节介绍相关工作，引出第2节的MSF模型，第3节汇总实验结果并分析，第4节总结并提出未来的工作方向。

1 相关工作

嵌入模型的基本思路是学习KB中节点和关系的低维矢量表示，保留原有结构信息和知识约束[22]。目前可大致分为基于平移和基于张量/矩阵分解两类。

基于平移的方法将关系平移后的实体距离作为评分依据，如TransE将三元组的头尾实体和关系映射为低维向量h,t和r，相异度得分函数如公式1所示：

score1=‖h+t-r‖p，

(1)

其中，p为L1或L2范数，但由于对称关系的向量映射趋向于零，TransE在对称模式上的学习能力不足，在处理复杂关系类型时表现欠佳；TransH为解决上述问题，将头/尾实体向量映射到不同的关系超平面，体现相同实体对应不同关系时的角色差异[23]；TransR[24]进一步使用矩阵M代替超平面，将得分函数设定为‖Mrh+r-Mrt‖p；类似模型如STransE[25]等在提升表达能力的同时，往往伴随着复杂度的增加；TransD和TranSparse等则尝试降低计算开销[26-27]。该类模型多使用基于间隔排序标准(margin-based ranking criterion)的损失函数。RotatE将平移和旋转结合，使用Hadamard积将头/尾实体距离定义为复数空间中的旋转向量关系[28]。

张量分解方法往往在初始化嵌入表示的基础上进行乘法/点积运算，如DistMult将关系表示为对角矩阵，将嵌入向量的Hadamard积作为三元组得分，但由于计算不受参数顺序影响，DistMult无法识别头/尾实体调换的情况，难以学习反对称模式；ComplEx[29]使用共轭复数解决该问题，将实体嵌入到复数空间中，但在学习组合模式映射时效率较低，且存在冗余计算；DistMult和ComplEx可视作RESCAL[30]的关系矩阵降维版本；另一双线性模型SimplE[31]在传统Canonical Polyadic (CP)模型的基础上改进，引入反向模式解决表示学习孤立的问题，为关系也学习2种向量表达，引入权重系数调整三元组得分比例，但没有建模双射映射，在处理组合模式时同样存在性能瓶颈。

本文在平移/旋转嵌入的基础上，尝试为多种关系模式引入不同的得分函数，通过训练实体的多种嵌入表达并在整体得分函数中集成，提高潜在特征的提取能力，同时将计算开销限制在线性增长的范围内；此外本文采用了基于阈值限制的损失函数以提高知识表达和推理性能。

2 MSF模型

将三元组表示为(h,r,t)，h和t分别对应头、尾实体，实体间关系r表示为节点间的边，h,t∈，r∈。嵌入的本质是将实体或关系依据其潜在特征映射为低维表示，依据选取的模型，其表示可能是向量e/r(如es,et分别表示头、尾实体)、矩阵M或张量。知识表达和推理通过三元组嵌入表示和预测评分实现，即将三元组映射为r(es,et)，并通过评分判断其是否成立。

本文的主要特色和设计思路在于：1)为多种关系模式使用不同的得分函数，集成方法确保背景知识映射到嵌入表示的同时增强模型稳定性；2)使用基于阈值限制的损失函数。关系模式的相关定义和得分函数的映射能力推导如下：

Definition 1(Symmetric Mode, 对称模式):ris symmetric when

ifr(h,t) holds, thenr(t,h) holds for ∀h,t；

Definition 2(Anti-Symmetric Mode, 反对称模式):ris anti-symmetric when

ifr(h,t) holds, thenr(t,h) doesn’t hold for ∀h,t；

Definition 3(Inverse Mode, 反向模式):r1,r2are inverse when

ifr1(h,t) holds, thenr2(t,h) holds for ∀h,t；

Definition 4(Composition Mode, 组合模式):r3is composed ofr1andr2when

ifr1(h,t)&r2(t,j) holds, thenr3(h,j) holds for ∀h,t,j；

Definition 5(Reflexive Mode, 自反模式):ris reflexive when

ifr(h,h) holds for ∀h；

反向关系模式如isParentOf和isChildOf，若isParentOf(a,b)成立，即a为b的父母，则isChildOf(b,a)也成立，即b为a的子女。该模式使用与TransE相同的score1评分函数；反对称模式和组合模式也一样。

对称关系模式如marriedTo，若marriedTo(a,b)成立，即a、b为婚姻关系，则marriedTo(b,a)也成立。对于该模式，若采用与TransE相同的评分函数，则r在学习过程中将向零向量趋近，进而对实体的嵌入表示造成影响，因此使用score2，如式(2)所示：

score2=‖h+t-r‖p

(2)

TransE系列模型难以学习自反关系模式，或无法识别对称性和迁移性；理论上具备完整表达能力的模型如ComplEx复杂度较高且实际结果难以预料。本文使用与RotatE类似的得分函数score3，但定义在实数空间中，同样采用Hadamard积，如公式3所示：

score3=‖h○r-t‖p

(3)

3种得分函数及其处理的关系模式的几何表示如图1所示。

图1 关系模式的几何表示Fig.1 Geometric illustration of various relational modes

引理1score1函数可用于建模反对称、反向和组成模式，证明如下

反对称模式：

ifr1(ei,ej)&r1(ej,ei) ，

(ei+r1=ej)∧(ej+r1≠ei)⟹ei+2r1≠ei。

反向模式：

ifr1(ei,ej)&r2(ej,ei) ，

(ei+r1=ej)∧(ej+r2=ei)⟹r1=-r2。

组合模式：

ifr1(ei,ej)&r2(ej,ek)&r3(ei,ek) ，

(ei+r1=ej)∧(ej+r2=ek)∧(ei+r3=ek)⟹r1+r2=r3。

引理2score2函数可学习对称模式嵌入，证明如下

ifr1(ei,ej)&r1(ej,ei) ，

(ei+ej-r1=0)∧(ej+ei-r1=0)⟹ei+ej=r1。

同理可证，该函数难以学习反对称关系模式。

引理3使用score3函数学习自反模式的映射，一定是对称且可迁移的，证明如下

对称性：

ifr1(ei,ei)&r1(ej,ej) ，

(eir1=ei)∧(ejr1=ej)⟹r1=U⟹eir1≠ej。

迁移性：

ifr1(ei,ej)&r2(ej,ek),r1(ej,ei)&r2(ek,ej) ，

(eir1=ej)∧(ejr2=ek)⟹(eir1r2=ek)∧(r1,r2=U)⟹ei=ek。

score3理论上具备自反模式的学习能力，但可能也适用于其他关系模式，因为类似的RotatE模型[28]在Countries数据集的多个组合模式上都取得了突出结果。实验验证该假设。

MSF模型使用多目标函数进行联合优化训练；在SimplE基础上，对相同的实体/关系训练不同的向量表示以契合其所在三元组的关系模式，在整体得分函数中进行关联集成。本文使用3个嵌入向量e1,e2,e3∈d表示每个实体h,t，r1,r2,r3∈d表示每个关系r。

整体得分函数定义为得分函数的加权，如式(4)所示，使用TanhShrink非线性激活函数处理累加得分(实验中效果优于tanh)，思路是某个得分函数识别出某种模式并判定三元组成立，整体得分也会相应变化；w1,w2,w3分别对应3种函数的权重，与φ一同随机初始化，并在神经网络的训练过程中与嵌入向量学习一同优化。

f=TanhShrink(‖w1score1‖p+‖w2score2‖p+‖w3score3‖p+φ)

(4)

本文使用了基于阈值限制的损失函数以确保有效三元组的得分低于阈值，同时使无效三元组的得分高于另一阈值，阈值通过训练生成，函数设计如式(5)所示：

(5)

其中，α1,α2>0，表示有效/无效样本对应的权重系数；T+,T-分别表示有效/无效样本集；[.]+=max(., 0)；γ1,γ2∈+，训练中调整并选定设置轮数epochs内的最优值，TanhShrink函数可扩大γ1,γ2的取值区间；多次迭代可确保梯度下降的结果中有效样本的得分低于γ1，而无效样本得分高于γ2。

RESCAL、NTN模型的时间复杂度较高。TransE、DistMult、ComplEx、ConvE和RotatE等模型都将复杂度控制在O(d)级别上，d为嵌入维度。本文使用的多组向量表示对应复杂度为线性增长，同样为O(||d+||d)。

3 实验结果与分析

链路预测从已知信息中推理新的事实，用于知识补全，方法是计算给定头/尾实体与特定关系构成三元组的得分，用于判定三元组是否有效。实验使用MR(平均排名)、MRR(平均倒数排名)和Hits@10(排名在前10位的正确实体的比例)作为评估指标(均为filtered)。MR排序越低越好；MRR和Hits@10得分越高越好。本文所用的数据集统计信息如表1所示；除了FB15k和WN18外，进一步使用FB15k-237和WN18RR以防止算法高分漏洞[32]。各模型的训练策略如表2所示。

表1 数据集统计信息

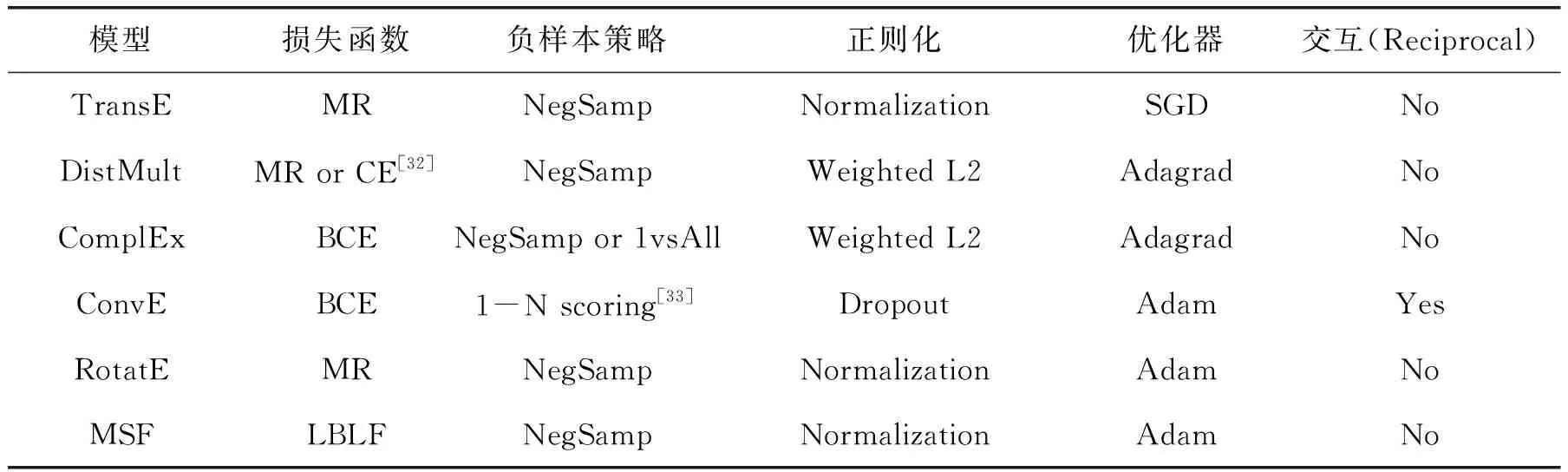
表2 各模型的训练策略

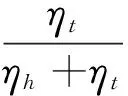
其他模型使用原研究的实现和超参池设置。使用PyTorch实现MSF模型，使用Adam优化器[34]，初始超参数池设置如下：batch size∈[512, 1 024, 2 048]，learning ratelr∈[1e-5, 1e-4, 5e-4] (Adam其他参数默认)，d∈[50, 100, 200]。所有模型使用Ax框架(https://ax.dev)进行随机参数组合并根据验证集上的性能表现选择最佳参数，若最后10轮对应MRR提升<10-2则停止训练。MSF在WN18上取得最佳性能表现时，[d,α1,α2,γ1,γ2]分别为[100, 2, 1, 2, 2]；FB15k上为[200, 1, 1, 10, 12]；WN18RR上为[50, 4, 1, 2, 2]；FB15k上为[100, 1, 1, 9, 9]。使用L2范数，习得的[w1,w2,w3,φ]分别为[0.31, 0.22, 0.47, 1]。

实验结果如表3、表4所示。TransE在WN18和WN18RR上与其他模型存在明显差异，验证了平移模型在稠密数据集上存在学习能力不足的问题(相似实体的嵌入表示趋近)。双线性模型DistMult和ComplEx擅长提取实体相似性特征，在WN18和WN18RR上表现较好，但在FB15k和FB15k-237上则难以提取足够的信息以优化嵌入表示，性能下滑。ConvE的整体结果优于ComplEx，但有一定波动，说明尽管对实体/关系向量的拼接和二维转化有助于CNN提取局部模式和关系特征，但有可能丢失全局特征。在WN18和FB15k上，MSF和ConvE、RotatE模型的性能接近；但在更符合现实应用场景的WN18RR和FB15k-237数据集上，MSF的整体结果具备明显优势。在所有4个数据集上，MSF的MR排序得分均为最优，说明其单次排序的结果较稳定。在WN18RR和FB15k-237复杂数据集的MR得分上，RotatE和ComplEx、ConvE的差异可能是来自不同的无效样本生成策略：RotatE使用大量无效三元组辅助训练，有助于提升其得分。MSF的无效三元组比例低于RotatE，维度d也远小于ComplEx和ConvE，在降低计算开销的同时保证了模型性能，验证了多重得分函数集成的可行性。

表3 WN18和FB15k上的实验结果

表4 WN18RR和FB15k-237上的实验结果

各模型在不同数据集上的训练和预测用时与预期接近，MSF时间开销与主流模型在同一量级上，结果略。WN18RR和FB15k-237数据集上不同参数选择对模型性能的影响如图2、图3所示，除TransE受训练策略和损失函数约束，仅使用40种随机参数组合外，其他模型的参数配置数约150种。可见模型性能受参数设定影响大，且以中位数为性能量度时，MSF模型较稳定。

图2 WN18RR上MRR分布受参数选择的影响Fig.2 MRR distribution over hyperparameter configuration on WN18RR

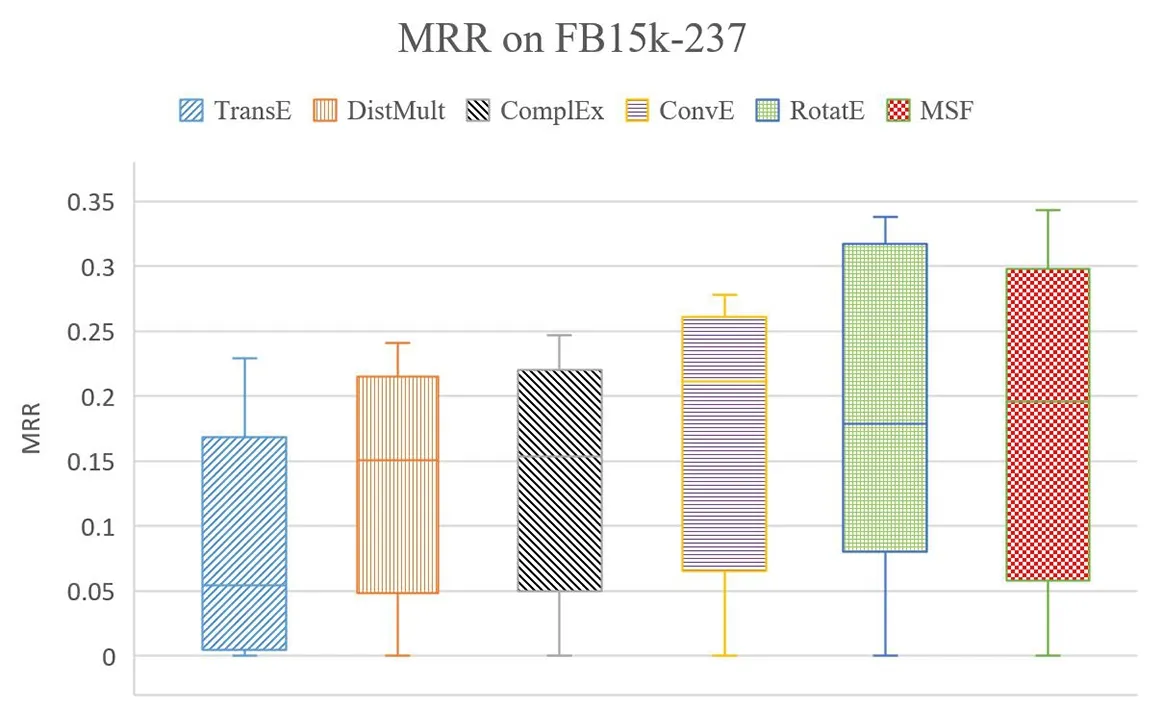
图3 FB15k-237上MRR分布受参数选择的影响Fig.3 MRR distribution over hyperparameter configuration on FB15k-237

WN18RR和FB15k-237数据集上各模型MRR得分随Epoch变化的情况如图4、图5所示，可见MSF相比其他模型，取得稳定MRR得分的速度无明显劣势。

图4 WN18RR上MRR得分随轮数的变化情况Fig.4 MRR over various epochs on WN18RR

图5 FB15k-237上MRR得分随轮数的变化情况Fig.5 MRR over various epochs on FB15k-237

在Sun等定性分析各数据集关系模式组成的基础上[28]，本文进一步量化计算了各模式比例，并根据各模型的理论特性重点研究其在对称/反对称/自反关系模式上的性能表现[28]。WN18和WN18RR数据集中无自反模式关系，而对称模式比例较高，故在这两个数据集上比较对称和反对称模式的表现，在FB15k和FB15k-237数据集上比较自反模式的表现，结果如表5所示，可见TransE模型在学习对称模式时确实存在困难；DistMult在处理反对称模式时表现略差；各模型在自反模式上的性能仍有待提高，尤其是TransE和ComplEx模型，而集成多重得分函数的MSF模型保持了整体的稳定性。

表5 不同关系模式下的MRR得分比较

为进一步评估不同得分函数对模型性能的影响，表6、表7分别展示了WN18RR和FB15k-237数据集上单一得分函数，以及去掉单个得分函数后MSF模型的性能表现；轮数均为300。可见score3函数对模型性能的影响最大，具备多种关系模式的学习能力；score1、score2对整体模型的影响较小，score2可能仅适用于对称模式的表示学习。

表6 WN18RR和FB15k-237上单一得分函数的模型性能

表7 WN18RR和FB15k-237上不含特定得分函数的模型性能

4 结语

针对单一得分函数难以学习多种关系模式的问题，本文设计了基于平移/旋转嵌入的MSF表示模型，使用神经网络为不同评分函数训练独立的向量表示，同时使用基于阈值限制的损失函数提高知识表示和推理能力。理论推导和实验结果表明MSF模型可学习对称、反对称、反向、组合、自反等多种关系模式的嵌入映射。后续工作考虑评估与提升模型在复杂关系类型(如非交换组合模式)上的处理能力；优化无效样本生成策略[28]；借鉴其他关系学习模型[35]的优点；以及在更大规模的数据集如FC17[36]上进一步比较、验证和优化方案性能等。