基于模糊自适应改进的四旋翼串级控制器的研究

林宗炮，郑祥盘

(1.福州职业技术学院机器人学院，福建 福州 350108；2.闽江学院物理与电子信息工程学院，福建 福州 350108)

0 引言

近年来，四旋翼无人飞行器由于其能够实现垂直起降和空中定点悬停以及原理简单、便于维修等优点，目前已被广泛应用于航拍摄影、城市管理、农林植保、电力巡检等领域[1]。但同时，它是通过4个螺旋桨产生的升力和转矩实现六自由度(位置和姿态)飞行的，水平位置与滚转和俯仰角动态耦合，是一种典型的四输入六输出的多变量、欠驱动、强耦合的非线性系统[2-4]，这些特点使得控制器的设计变得尤为关键。

针对四旋翼无人机的上述特点，国内外学者已经进行了大量的研究。文[5-6]应用单回路PID控制器实现四旋翼无人机的高度和姿态控制的方法。仿真结果表明，PID控制器具有一定的自适应能力和鲁棒性。但是单回路PID控制器无法实现对四旋翼另两个自由度即水平方向的控制。文[7]应用反馈线性化方法将四旋翼飞行器的非线性姿态模型转化为线性模型，然后利用误差反馈控制律设计了线性控制器。但是结果显示其对系统建模不确定性和传感器测量噪声鲁棒性较差。文[8]提出了一种基于李亚普诺夫稳定性理论的滑模控制器，结果表明滑模控制器在有噪声的情况下具有良好的轨迹跟踪和良好的鲁棒性。针对四旋翼无人飞行器欠驱动特性的问题，文[9]提出了位置和姿态级联控制结构，即位置控制器生成了期望的滚转和俯仰角提供给姿态控制器使用，解决了四旋翼无人飞行器四输入六输出欠驱动的问题。斯坦福大学的 STARMAC 项目采用强化学习法作为四旋翼无人飞行器的控制算法，实现了与其他类型的小型无人飞行器协同作业[10]。

本文考虑了方波脉冲跳变轨迹跟踪的控制问题，引入具有模糊自适应的智能控制技术和结构简单的传统PID控制技术双重优点的模糊自适应控制方法，提出了一种基于模糊自适应改进的内外环串级的分布式控制系统对四旋翼飞行器的运动状态进行控制。本文的主要贡献如下：

1)基于目前研究很少考虑四旋翼飞行器油门的控制分配和执行机构的现状，建立了包含四旋翼飞行器的非线性特征、位置和姿态控制器、油门的控制分配以及电机模型的仿真控制系统。

2)提出了一种基于模糊自适应改进的内外环串级的分布式控制方法对四旋翼飞行器的运动状态进行控制，实现了对四输入六输出欠驱动系统的位置和姿态的快速跟踪，保持了传统PID控制器和模糊自适应智能控制技术的优点。

3)在轨迹跟踪过程中，对比了两种控制算法在不同轨迹情况下的表现，从位置和姿态标准差角度入手，验证了所提出的控制方法的先进性，包括更好的鲁棒性和节能性。

1 四旋翼飞行器控制模型

如图1所示，为了平衡螺旋桨旋转产生的反扭转矩，规定对角位置的螺旋桨1和3旋转方向一致(逆时针旋转)，螺旋桨2和4旋转方向一致(顺时针旋转)。四旋翼飞行器的垂直运动是通过集体增加(上升)或降低(下降)4个螺旋桨的速度来实现的。悬停时，4个螺旋桨的转速应当相等。滚转运动是通过成对增加(右滚转)或者降低(左滚转)螺旋桨2和3的转速，对应地成对降低(右滚转)或者增加(左滚转)螺旋桨1和4的转速来实现的。俯仰运动是通过成对增加(上仰)或者降低(下俯)螺旋桨1和2的转速，对应地成对降低(上仰)或者增加(下俯)螺旋桨3和4的转速来实现的。滚转和俯仰运动又带动四旋翼飞行器的水平运动。偏航运动是通过成对增加(顺时针偏转)或者降低(逆时针偏转)螺旋桨1和3的转速，对应地成对降低((顺时针偏转)或者增加(逆时针偏转)螺旋桨2和4的转速来实现的[11-12]。

图1 四旋翼飞行器的惯性坐标系Fig.1 Inertial coordinate system of quadrotor aircraft

1.1 运动学模型

如图1所示，四旋翼飞行器“X”形配置，定义E={xe,ye,ze}为四旋翼机体质心的惯性大地坐标系，B={xb,yb,zb}为它的机体坐标系，Pe=[x,y,z]T∈3和Θe=[φ,θ,ψ]T∈3分别表示四旋翼飞行器在惯性大地坐标系中当前的位置和姿态，其中x为前后，y为左右，z为上下，φ为滚转角，θ为俯仰角，ψ为偏航角。Vb=[u,v,w]T∈3和Ωb=[p,q,r]T∈3分别表示在机体坐标系B中机体的线速度和角速度向量。则四旋翼飞行器质心的位置和姿态的运动学方程可表示为[11-13]

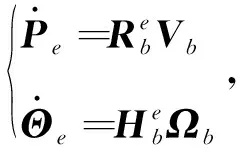
(1)

(2)

(3)

为表示方便，简记s=sin,c=cos,t=tan等。

1.2 动力学模型

根据牛顿-欧拉方程，在施加于四旋翼飞行器质心的外力作用下(忽略空气阻力和地面效应以及参数的不匹配)，机体坐标系B中的刚体动力学方程可表示为[11-13]

(4)

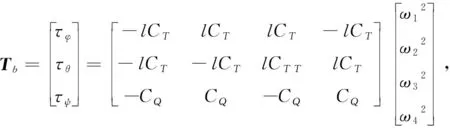
(5)

(6)

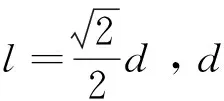
结合式(1)～(6)，可以得到四旋翼飞行器的六自由度动力学模型为[11-15]

(7)

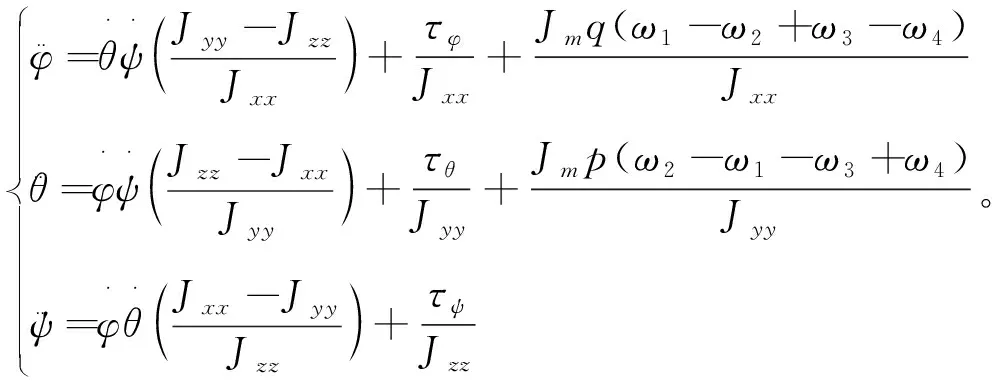
(8)

2 控制器设计

四旋翼飞行器从上述动力学角度分析，是四输入六输出的欠驱动的不稳定的系统，因此，设计使系统稳定的控制算法就尤为关键。将通过内环和外环串级分布式控制系统对四旋翼飞行器的运动状态进行控制(图2)。外环控制器输入为期望的位置Pd=[xd,yd,zd]T，期望的偏航角ψ和当前的水平位置x、y，水平方向当前的线速度u、v以及当前的偏航角ψ，输出为期望的滚转φd，俯仰θd和偏航角ψd及期望高度zd。内环控制器输入为期望的姿态角Θd=[φd,θd,ψd]T，期望的高度zd和当前的姿态角Θe=[φ,θ,ψ]T，当前的角速度Ωb=[p,q,r]T以及当前的高度z和垂直方向当前的线速度w,输出为期望的中间虚拟控制量Ui。经过控制分配模块和电机模型分别得到期望的油门控制量和期望的电机转速。最后期望的电机转速输入到四旋翼飞行器模型，模拟四旋翼飞行器的运动特性。

图2 四旋翼飞行器的串级分布式控制系统Fig.2 Cascade distributed control system of quadrotor aircraft

2.1 PID控制器设计

定义期望位置和期望姿态为Xd=[xd,yd,zd,φd,θd,ψd]T∈3，误差为xerr=xd-x，yerr=yd-y，zerr=zd-z，φerr=φd-φ，θerr=θd-θ，ψerr=ψd-ψ，则惯性大地坐标系中水平方向的误差xerr和yerr映射到机体坐标系B中的误差为

xb_err=xerrcψ+yerrsψ，

(9)

yb_err=-xerrsψ+yerrcψ。

(10)

定义机体坐标系B中机体的线速度误差为uerr=xb_err-u，verr=yb_err-v，则设计外环PID控制律产生期望的虚拟滚转和俯仰角为

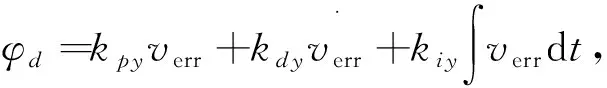
(11)

(12)

设计内环PID控制律(包括高度和姿态)产生期望的中间虚拟控制量Ui(i=1,2,3,4)：

(13)

(14)

(15)

其中，kpx、kdx、kix和kpy、kdy、kiy以及kpz、kdz、kiz分别是x，y，z方向上的比例、微分和积分系数，kpφ、kdφ、kiφ和kpθ、kdθ、kiθ以及kpψ、kdψ、kiψ分别是姿态角φ，θ，ψ的比例、微分和积分系数，根据Hurwitz判据，合适的选择式(9)～(14)中大于0的比例、积分和微分系数,最终都会收敛到期望位置和期望姿态[16-17]。

2.2 基于模糊自适应改进的PID控制器设计

如图3所示，基于模糊自适应改进的PID控制器选择二输入三输出的结构，系统误差e和误差变化率ec作为输入，3个输出Δkp、Δki、Δkd乘上量化因子α、β、γ作为比例系数、积分系数和微分系数的修正值，对PID控制器的kp、ki和kd3个参数进行在线调整，从而使控制系统具有良好的动、静态性能。

图3 基于模糊自适应改进的PID控制器的结构Fig.3 Structure of PID controller based on fuzzy adaptive improvement

e、ec、Δkp、Δki、Δkd的论域定义为：{-1，-2/3，-1/3，0，1/3，2/3，1}，其模糊子集为{NB，NM，NS，ZO，PS，PM，PB}，子集中元素分别代表负大、负中、负小、零、正小、正中、正大[18-19]。

e、ec、Δkp、Δki、Δkd隶属函数如图4所示。

图4 e、ec、Δkp、Δki、Δkd隶属函数Fig.4 e、ec、Δkp、Δki、Δkdmembership function

输出变量Δkp、Δki、Δkd的模糊控制规则如表1～表3所示，去模糊化采用面积中心法。

表1 Δkp的模糊规则表

表2 Δki的模糊规则表

表3 Δkd的模糊规则表

2.3 控制分配设计

4个电机期望的油门控制量Γi(i=1,2,3,4)可以设计为

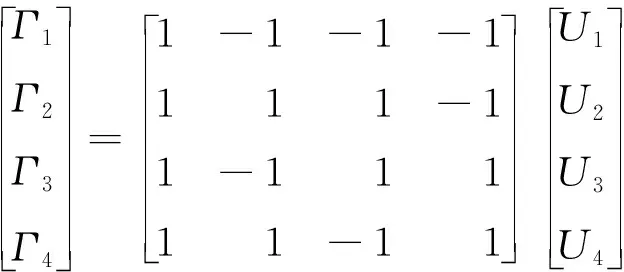
(17)

3 实验结果与分析

为了验证上述控制器设计的有效性和先进性，对四旋翼无人机进行控制仿真，设计基于内外环都是传统PID(以下简称PP控制器)和内外环都是模糊自适应改进PID的串级分布式控制器(以下简称FF控制器)进行对比分析。其中四旋翼无人机的模型参数如表4所示，PP和FF控制器的参数如表5所示。假设初始值为Pe(0)=[0,0,3]T，Vb(0)=[0,0,0]T，Θe(0)=[0,0,0]T,ω(0)=[4 000,4 000,4 000,4 000]T，Ωb(0)=[0,0,0]T[12]。期望的偏航角度ψd=0,期望跟踪的水平方向位置xd和yd前20 s是幅度为2 m,周期为10 s,占空比为50%的方波，后20 s是幅度为3 m,周期为10 s,占空比为50%的方波,最后5 s是0位置。期望跟踪的垂直方向位置zd初始值是3 m,前20 s是幅度为2 m,周期为10 s,占空比为50%的方波，后20 s是幅度为3.5 m,周期为10 s,占空比为50%的方波，最后5 s是初始位置3 m。

表4 四旋翼无人飞行器的模型参数[12]

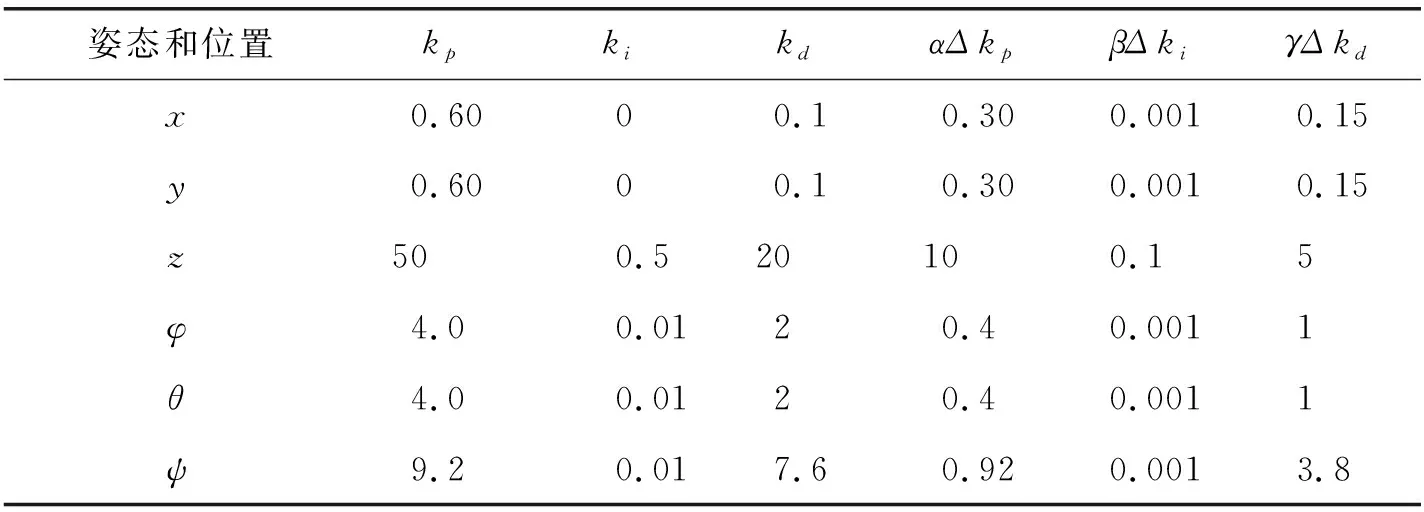
表5 PP和FF控制器的参数

四旋翼无人飞行器在PP和FF两种不同控制器作用下，期望位置的跟踪和姿态角的动态响应过程的仿真结果如图5和图6所示，期望位置的超调量(σ)和上升时间(tr)如表6所示，姿态角的变化范围如表7所示，位置和姿态角的标准差如表8所示。

表6 两种控制器方式下的超调量(σ)和上升时间(tr)

表7 两种控制器方式下姿态角的变化范围

表8 两种控制器方式下位置和姿态角的标准差

图5所示描述了四旋翼无人飞行器在PP和FF两种不同控制器作用下期望位置的轨迹跟踪过程。在前20 s，两种控制方式都实现了期望轨迹的跟踪，在后20 s，基于PP控制器的控制方式振幅和超调量非常大，特别是水平方向处于失控的边缘，而基于模糊自适应改进的FF控制器，较好地实现了期望轨迹的跟踪，它们的超调量和上升时间如表6所示。可以看出，不管是前20 s跟踪幅值为2 m的方波，还是后20 s跟踪轨迹突变的方波，基于模糊自适应改进的FF控制器，都可以实现自动对PID参数的优化调整，具有更为平稳的动态响应。特别是在后20 s轨迹出现突变的时候，基于模糊自适应改进的FF控制器，鲁棒性能更好。但同时，发现基于模糊自适应改进的FF控制器，上升时间比基于传统PID实现的控制器的更长，这是由于引入了模糊控制器导致的延迟。

图5 两种控制器方式下的期望位置跟踪对比Fig.5 Comparison of desired position tracking under two controller modes

图6所示描述了四旋翼无人飞行器在PP和FF两种不同控制器作用下姿态角的动态响应过程。可以看出，基于模糊自适应改进的FF控制器在四旋翼无人飞行器角度修正过程中，相对基于传统PID控制的PP控制器，需要修正的角度较小，两种控制器方式下姿态角的变化范围如表7所示。结合表8，可以得出，基于模糊自适应改进的FF控制器在四旋翼无人飞行器角度修正过程中，由于引起较小的角度修正，控制器的控制量变化更小，因此能量消耗更少。

图6 两种控制器方式下的姿态响应曲线对比Fig.6 Comparison of attitude response curves under two controller modes

综上所述，可以得出以下结论：

1)基于模糊自适应改进的内外环串级PID控制器在一定条件下可以实现自动对PID参数的优化调整。

2) 以上实现的两种控制方法都具有一定的鲁棒性，相对来说，基于模糊自适应改进的内外环串级PID控制器的鲁棒性能更好。

3) 相对传统的PID控制器，基于模糊自适应改进的内外环串级PID控制器在四旋翼无人机角度修正过程中，控制量变化更小，能量消耗更少，理论待机时间更长。

4 结语

为了解决四旋翼飞行器四输入六输出欠驱动的问题，本文提出了一种基于模糊自适应改进的内外环串级的智能控制方法。仿真实验结果表明，该方法优于传统的基于内外环串级的PID控制，可以实现自动对PID参数的优化调整，具有更好的轨迹跟踪能力和鲁棒性能以及更好的控制品质，无人机能量消耗更少，理论待机时间更长。