标志中的数学文化*
2022-04-21童广鹏河南省民权县高级中学476800
中学数学 2022年4期
童广鹏 (河南省民权县高级中学 476800)
标志是生活中人们用来传播某一事物信息特征的记号,包含数学文化元素的视觉标志已被广泛应用于社会诸多领域,对人类社会的发展与进步愈发彰显其巨大魅力.下面结合几款标志从数学文化角度分析之.
1 Kappa标志
例1
运动及休闲服装品牌Kappa的logo标志(图1)可抽象为如图2所示的靠背而坐的两条优美的曲线,则下列函数中大致可“完美”局部表达这对曲线的是( ).
图1 图2
解析 由图象可知,函数y
=f
(x
)为偶函数,且在x
=0右侧附近的函数值为正.对于BC选项,函数都为奇函数,不合题意.AD选项都是偶函数,当时,对于A选项,sin 6x
>0,且2--2<0,故不合题意,A选项错误;对于D选项,cos 6x
>0,即选项正确.命题背景
此标志产生于1969年,一对男女模特在Kappa工作间隙坐下来休息,摄影师无意中捕捉到了背靠背画面,由此诞生了这个享誉世界的品牌logo.此标志反映了人与人之间相互依靠、互助的精神,此充满浪漫色彩的品牌标志一直沿用至今,成为风靡世界的视觉符号.借助于数学文化的渗透,通过视觉化呈现出标志的内涵,彰显出超越时间与空间的对称之美.2 苹果标志
例2
苹果公司的logo标志是用一系列以1,2,3,5,8,13,…为半径的圆截得的(图3),右上方是三个半径为8的圆,自上而下依次为圆A
、圆B
、圆C
,已知它们的圆心在斜率为-1的同一直线上,圆A
与x
轴相切于坐标原点O
,且圆A
的圆心在x
轴上方,圆B
与y
轴相切,且圆心在y
轴右侧,圆C
与圆B
外切.
图3 图4
(1)求圆A
与圆B
的公共弦所在直线方程;(2)写出圆C
的标准方程(不用写过程).解析 由已知建立如图4所示的平面直角坐标系.
(1)因为圆A
与x
轴相切于点O
,圆心A
在x
轴上方且r
=8,所以圆A
:x
+(y
-8)=64,而A
,B
,C
三点共线且其斜率为-1,故l
:y
= -x
+8.又因为圆B
与y
轴相切且r
=8,圆心B
在y
轴右侧,所以圆心B
应在x
=8上,故从而圆B
:(x
-8)+y
=64.将两圆方程作差得16x
-16y
=0,即圆A
与圆B
的公共弦所在直线方程为y
=x
.(2)圆
命题背景
苹果logo标志的寓意是一个被上帝咬了一口的苹果,以此凸显苹果公司的理念是只有不完美才能促使进步并去追求完美.可见,数学文化与艺术形式美的完美契合,使得标志艺术获得了形式上永恒的生命.3 DS标志
例3
图5是法国品牌轿车DS的标志,此标志中左右对称的两条黑色曲线可以近似地看成双曲线的部分图形.若左边等腰三角形的两腰所在直线是双曲线的渐近线,且等腰三角形的底约为4个单位,高约为3个单位,则双曲线的离心率为( ).
图5
解析 由于双曲线的渐近线斜率为且等腰三角形的底约为4个单位,高约为3个单位,则即离心率故选A.
命题背景
标志设计发展到今天,其内在艺术已经远远超越了诞生之日的范围,尤其是将标志造型商业化,给各个企业带来了巨大的利润.在本题中DS是法国汽车工业顶级设计豪华品牌,在法语中乃“女神”之意.此标志左右两侧形似字母D,S,尤其是左右两侧双曲线的运用,使得标志呈现出无法超越的和谐之美.4 绿叶标志
例4
已知椭圆的面积为πab
.某数学爱好者设计了一个标志,如图6,在矩形OABC
中有一片绿叶图案标志,该叶片由函数y
=cosx
+1(x
∈[0,π])的图象及函数y
=的图象围成.今向该矩形内任投一点,则该点落在叶片图内的概率为( ).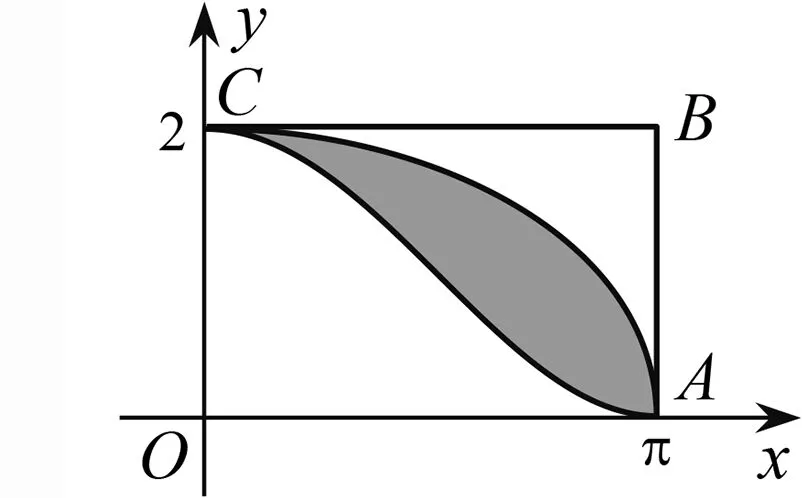
图6
解析 由题意矩形面积为2π,函数的图象为椭圆的该椭圆面积为2π.由余弦函数的对称性可知,函数y
=cosx
+1(x
∈[0,π])的图象与矩形围成的面积为矩形面积的一半,即为π,则S
故所求概率为选A.命题背景
本题以数学文化为支撑点,在形的高度和概括的基础上,打破了流于简单的正方形设计,突出了标志的简洁美.以清新简洁、明晰易记的数学设计,使绿叶标志作品富于了变化,丰富了内涵,拥有一种令人赏心悦目的美感,实现了超越时空的传播.