基础颗粒数量组合对颗粒黏结模型精度的影响

王 晓，薛玉君，程 波，刘 俊，官志强，李济顺

(1. 河南科技大学 a.机电工程学院,b.河南省机械设计及传动系统重点实验室，河南 洛阳 471003；2.洛阳矿山机械工程设计研究院有限责任公司，河南 洛阳 471003；3.矿山重型装备国家重点实验室(中信重工机械股份有限公司)，河南 洛阳 471003；4.School of Mechanical and Mining Engineering, University of Queensland, Queensland Brisbane 4702)

0 引言

矿石破碎特性对磨矿效率有决定性的影响，在实际生产中仅凭矿石粉碎特性试验得到的矿石特性参数无法准确达到理想的破碎效率[1-2]。矿石破碎过程的仿真是简化矿石破碎特性测定、便捷得到矿石破碎特性的有效方法，矿石破碎模型的精度直接决定了矿石破碎过程仿真的准确性[3-5]，建立符合实际矿石性质的颗粒黏结精确模型，有利于提高矿石破碎特性仿真的准确性，对矿石破碎特性及磨矿工艺参数的确定有着重要的应用价值[6-7]。因此,研究如何提高矿石破碎模型精度的方法有重要的工程应用价值。

离散单元法(discrete element method，DEM)广泛应用于各种领域的矿物破碎建模仿真研究[8-10]，其颗粒黏结模型能够通过不同颗粒间黏结键断裂过程表征实际矿石的破碎过程，可以更可靠地模拟矿物实际破碎效果[11-14]。因此，基于离散单元的颗粒黏结模型常被应用于矿石建模及其破碎特性研究。文献[15]对多尺度内聚颗粒模型的破碎过程进行了分析，通过模拟岩石轴压破碎试验得到的模型破碎裂纹形态与试验结果相似，验证了模型的可靠性。文献[16]分析了凝聚颗粒快速生成模型与碎片替换模型的优缺点，提出后续研究方向是模型设计和真实颗粒情况的结合与计算效率的提升。文献[17]提出了一种综合广义回归模型与粒子群算法的破碎粒度预测与优化模型，分析破碎产物粒度分布与给料粒度、冲击能耗等参数的关系，对破碎后粒度分布进行预测。文献[18]提出了多体颗粒破碎的弹簧-四面体单元模型，该模型能够反映颗粒破碎后的真实形状。综上所述，颗粒黏结模型在表征矿石内部复杂力学结构方面存在优势[19-20]，其中，模型参数是影响模型精度的关键因素。

本文针对颗粒黏结模型关键参数中的基础颗粒数量变化对模型精度的影响进行研究，采用离散元软件建立由不同数量基础颗粒所构成的矿石模型，并进行落重仿真，对比仿真与落重试验得到的破碎后粒度分布差异，分析基础颗粒数量组合对颗粒黏结模型精度的影响，得到符合实际矿石破碎特性的精度较高的颗粒黏结模型，为提高磨矿过程仿真的准确性提供研究基础。

1 基础颗粒数量组合方案

颗粒黏结模型的体积填充分数决定了基础颗粒总体积。为满足破碎后筛分粒级分布，实现破碎后颗粒团簇尺寸变化，实际操作中，选择3种基础颗粒进行组合，建立矿石颗粒黏结模型。颗粒黏结模型的体积取决于实际需要破碎的矿石尺寸，模型尺寸与实际矿石粒级相同，本文以实际矿石尺寸(粒径63～53 mm)为例，故所建模型为60 mm×60 mm×56 mm(长×宽×高)的六面体。

依据模型体积填充分数固定不变的原则，调整3种基础颗粒的数量形成基础颗粒数量组合。在基础颗粒填充的过程中，颗粒随机堆积于模型壳体中，后被压缩成实际物料模型尺寸。记3种基础颗粒为P1、P2、P3，粒径分别为d1=1 mm、d2=3 mm、d3=5 mm；取体积填充率α=0.6(来源于实际仿真)；设模型总体积为V，基础颗粒总体积为V0；P1颗粒单个体积为v1，总体体积为V1，个数为n1；P2颗粒单个体积为v2，总体体积为V2，个数为n2；P3颗粒单个体积为v3，总体体积为V3，个数为n3；则有：

V0=Vα；

(1)

V0=n1v1+n2v2+n3v3。

(2)

在填充率固定的条件下，基础颗粒数量的变化直接影响颗粒自然堆积高度，自然堆积高度过高或过低均会影响建模效果，其中，大尺寸基础颗粒的数量对自然堆积高度影响较大，故首先确定大尺寸基础颗粒P3的数量，然后改变基础颗粒P1、P2的数量，构成不同基础颗粒的数量组合。

实际仿真表明，大尺寸基础颗粒P3所占体积V3小于总体积V的50%时，自然堆积高度与模型实际高度差值小于10%，可以得到比较理想的仿真效果。这里取基础颗粒P3的数量为n3=1 500 ，则其所占体积比为48.67%。

若基础颗粒全部为P3时，即n1=0、n2=0，填充的基础颗粒总个数为n3=1 850。按总体积不变的原则将部分P3颗粒替换为P1颗粒和P2颗粒，若大尺寸基础颗粒P3的个数n3=1 500，P1颗粒个数n1=1 250，P2颗粒数量n2=1 574，基础颗粒组合的自然堆积高度为60.4 mm，略高于模型高度(56 mm)；若大尺寸基础颗粒P3的个数n3=1 500，P1颗粒个数n1=6 250，P2颗粒数n3=1 389，基础颗粒组合的自然堆积高度为58.9 mm，略高于模型高度(56 mm)；上述两种基础颗粒组合的自然堆积高度与模型高度(56 mm)的差值均小于10%，均在模型高度差允许的范围内。

为研究基础颗粒数量变化对仿真模型精度的影响，在基础颗粒自然堆积高度基本一致的情况下，对上述两种组合中的基础颗粒P1、P2的数量进一步分配，得到的5组基础颗粒数量组合见表1。

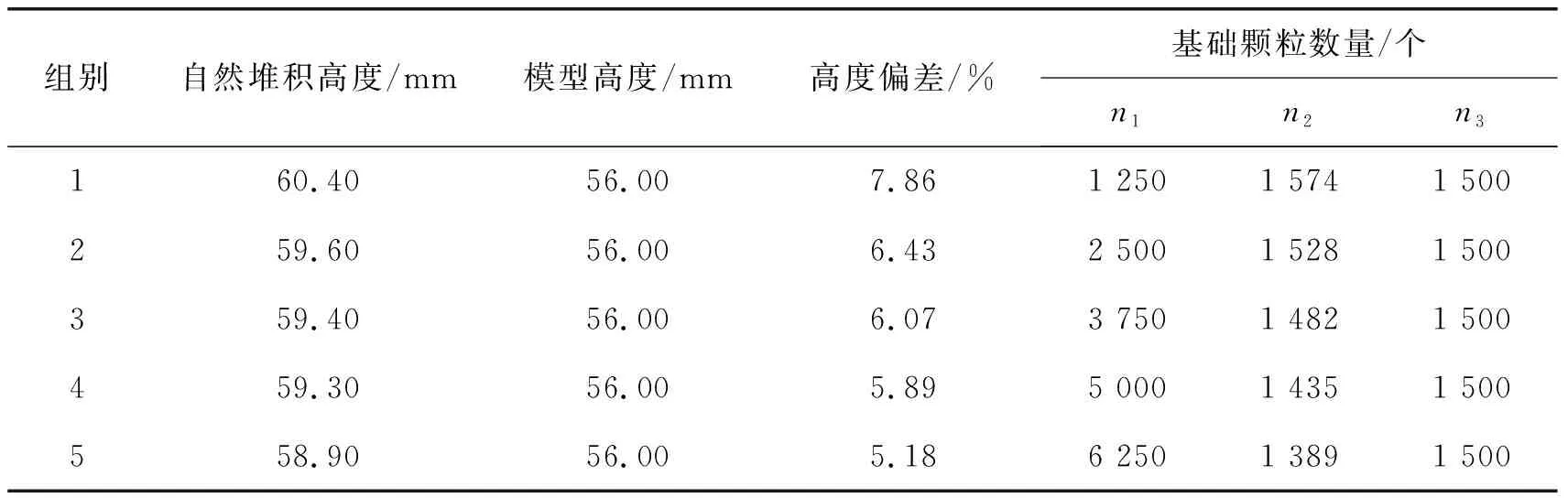
表1 基础颗粒数量组合

2 建立颗粒黏结模型及破碎仿真

2.1 建立颗粒黏结模型

基础颗粒间黏结键参数值因粒径不同而不同，不同粒径颗粒间黏结键参数也不同，均与颗粒组合顺序无关。3种粒径的基础颗粒间共需设置6种颗粒间黏结键，分别用K11、K22、K33、K12(K21)、K13(K31)、K23(K32)表示，其中,K11为P1颗粒间的黏结键，K22为P2颗粒间的黏结键，K33为P3颗粒间的黏结键，K12(K21)为P1颗粒与P2颗粒间的黏结键，K13(K31)为P1颗粒与P3颗粒间的黏结键，K23(K32)为P2颗粒与P3颗粒间的黏结键。由于不同矿石性质差异较大，黏结键参数通过数值试验方法[21]确定具体数值。设置的基础颗粒间黏结键参数如表2所示。

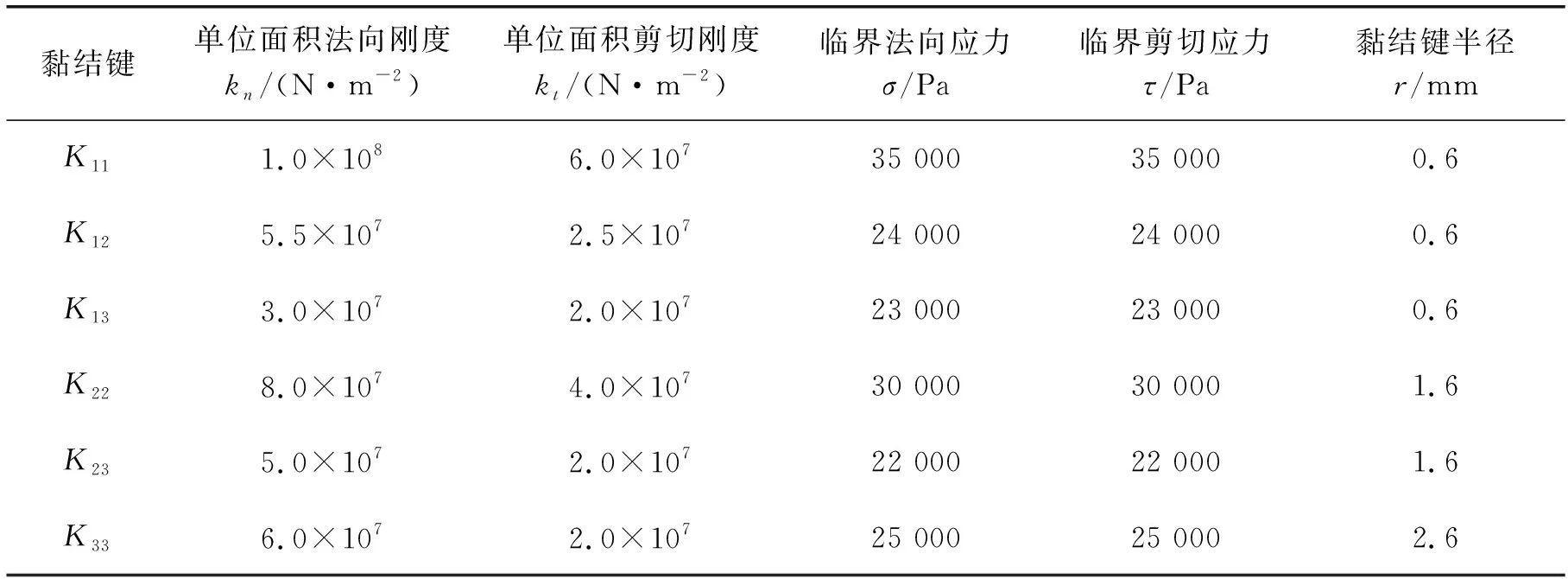
表2 颗粒间黏结键参数

依据5种基础颗粒数量组合(见表1)及黏结键参数(见表2)，可以建立5种颗粒黏结模型。

2.2 颗粒黏结模型破碎仿真

为方便描述，以表1中第3组基础颗粒数量组合为例，颗粒黏结模型破碎仿真过程如下：

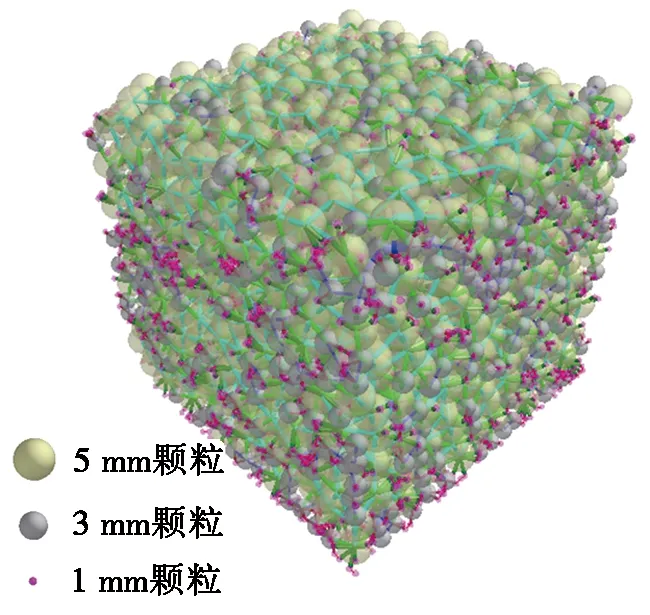
图1 矿石的颗粒黏结模型

依据表1中第3组基础颗粒数量及表2中颗粒间黏结键参数，用离散元法构建的颗粒黏结模型如图1所示，其中颗粒间的绿色圆柱为黏结键。

对该颗粒黏结模型进行不同冲击能量(E=0.10 kWh·t-1、0.25 kWh·t-1、0.40 kWh·t-1)下的落重仿真，得到破碎后不同粒度的颗粒团簇，如图2所示。根据最大直径对颗粒团簇进行分级，得到破碎后各粒级分布，对各粒级质量分数进行统计，得到模型破碎后各粒级质量占矿石总质量的百分数数据。图2a为冲击能量E=0.10 kWh·t-1时模型破碎结果，图2b为冲击能量E=0.25 kWh·t-1时，模型破碎结果,图2c为冲击能量E=0.40 kWh·t-1时模型破碎结果。随着冲击能量增大，颗粒团簇尺寸逐渐降低，大颗粒团簇数量减少。

(a) 冲击能量E=0.10 kWh·t-1

重复以上过程，分别构建表1中另外4种基础颗粒数量组合形式下的基础颗粒黏结模型，并进行落重仿真，得到破碎后各粒级质量分数。5组模型仿真破碎后各粒级质量分数见表3。由表3可知：颗粒数量变化时，破碎后颗粒团簇粒度分布出现变化，各组最大质量分数粒级各有不同，粒度分布区间不一致。

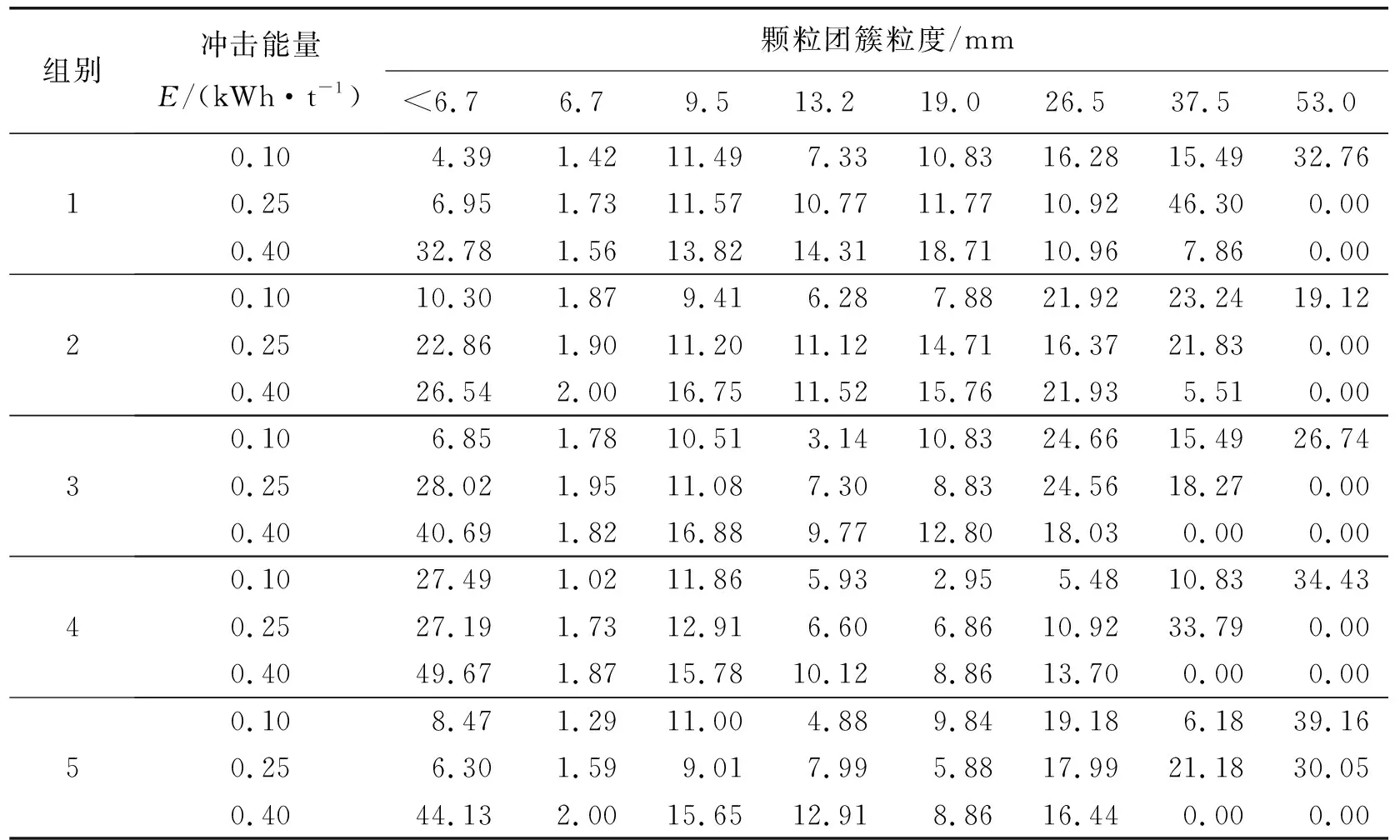
表3 仿真破碎后得到的各粒级质量分数 %

3 相同粒级金矿石落重试验

图3 落重试验机

为便于评价不同基础颗粒组合下的颗粒黏结模型精度，对颗粒黏结模型粒级一致的矿石(63～53 mm粒级金矿石)进行落重试验，落重试验在JKTech落重试验机(见图3)上进行。试验将30块金矿石试样分为3组，每组10块试样，冲击能量E=0.10 kWh·t-1、0.25 kWh·t-1、0.40 kWh·t-1。收集相同能量下的矿石碎块，在粒度筛分仪中进行粒度筛分，得到的试验粒度分布数据(10块试样的总值)见表4。由表4可知：3种冲击能量下，质量分数最大粒级分别为26.5 mm、26.5 mm和19.0 mm，破碎后最大粒度分别为53.0 mm、37.5 mm和26.5 mm。最小粒级质量分数随冲击能量增大而增加。

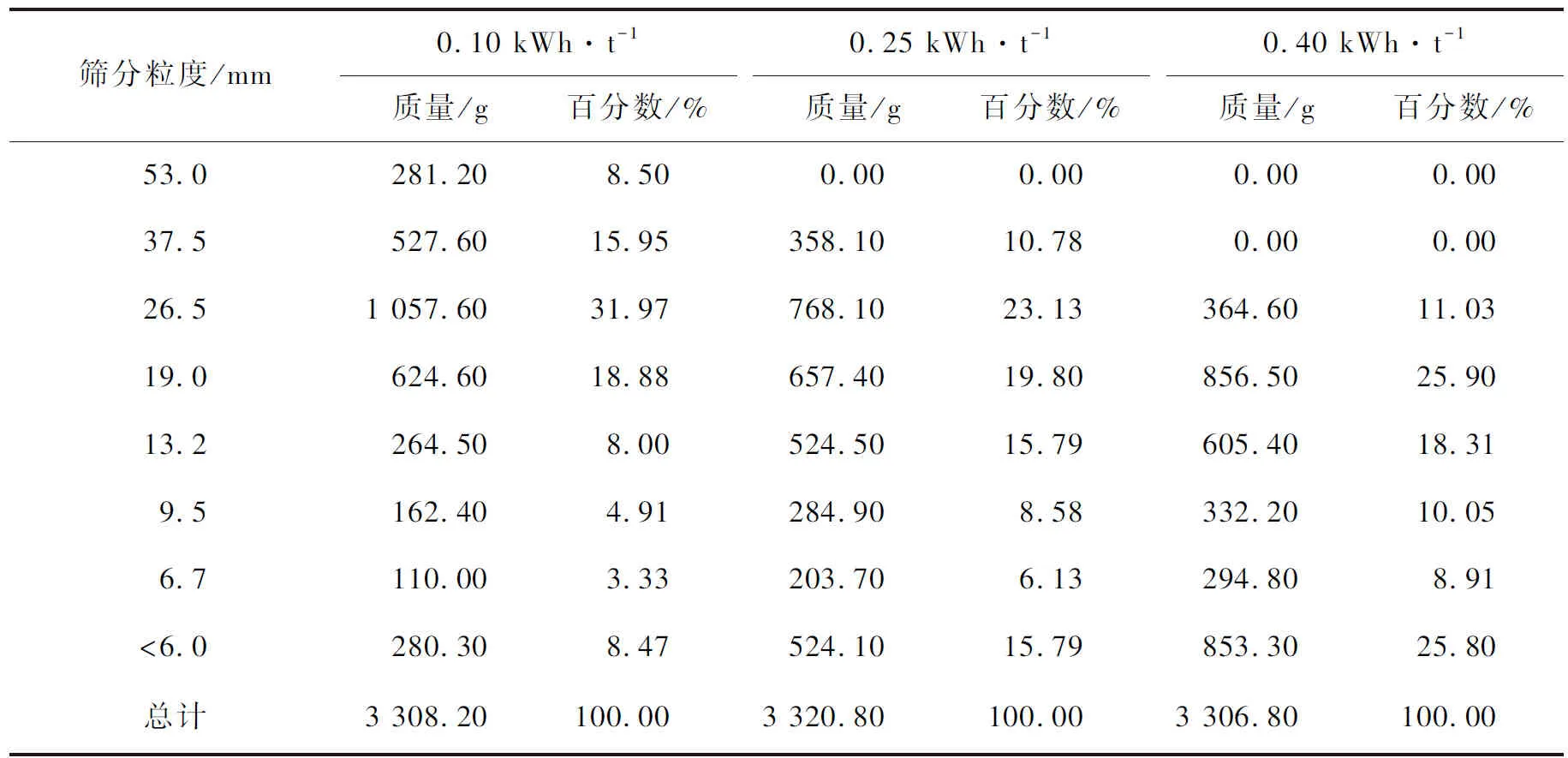
表4 63～53 mm粒级金矿石落重试验粒度分布

4 基础颗粒数量组合对颗粒黏结模型精度影响分析

4.1 破碎仿真与落重试验对比

破碎仿真与落重试验得到的粒度分布对比如图4所示。由图4a可知：冲击能量E=0.10 kWh·t-1时，9.5 mm粒度与53 mm粒度仿真质量分数与试验结果差异较大，破碎后大尺寸颗粒团簇质量分数较大。由图4b可知：冲击能量E=0.25 kWh·t-1时，大颗粒团簇质量分数随颗粒数量增加先增大后减小，曲线峰值向右偏移，颗粒团簇最大尺寸减小。由图4c可知：冲击能量E=0.40 kWh·t-1时，最大颗粒团簇尺寸减小，小粒度颗粒团簇质量分数变大，大颗粒团簇质量分数明显降低，曲线在中间粒度出现低谷，说明中间粒度质量分数不足。

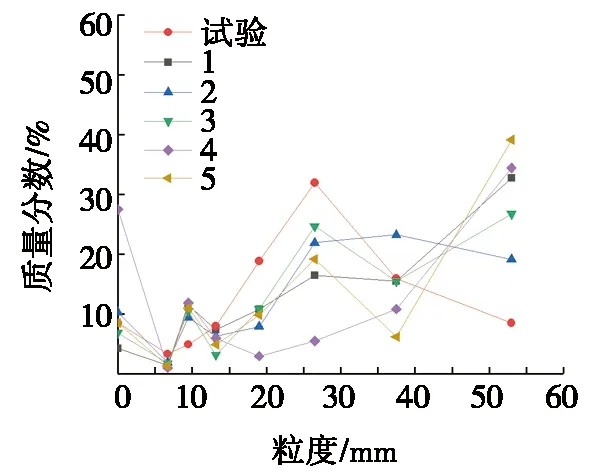
(a) 冲击能量E=0.10 kWh·t-1 (b) 冲击能量E=0.25 kWh·t-1 (c) 冲击能量E=0.40 kWh·t-1

4.2 仿真与试验结果的方差分析

仿真与试验结果的方差能够表征破碎仿真后各粒级质量分数分布曲线与试验结果的差异大小，差异越小，仿真模型精度越高，仿真效果越好。

不同组合下仿真与试验的质量分数方差S如图5所示。从图5中可以发现：在3种冲击能量下，基础颗粒数量组合2、3的方差较小。考察5种数量组合中P1颗粒总体积V1、P2颗粒总体积V2与P3颗粒总体积V3的体积比及各组合3种冲击能量下的平均方差(见表5)，可以发现当P2颗粒总体积分数与P3颗粒总体积比为0.21～0.22时，平均方差较小，说明模型精度较高，组别2与组别3之间应存在更优的基础颗粒数量组合。

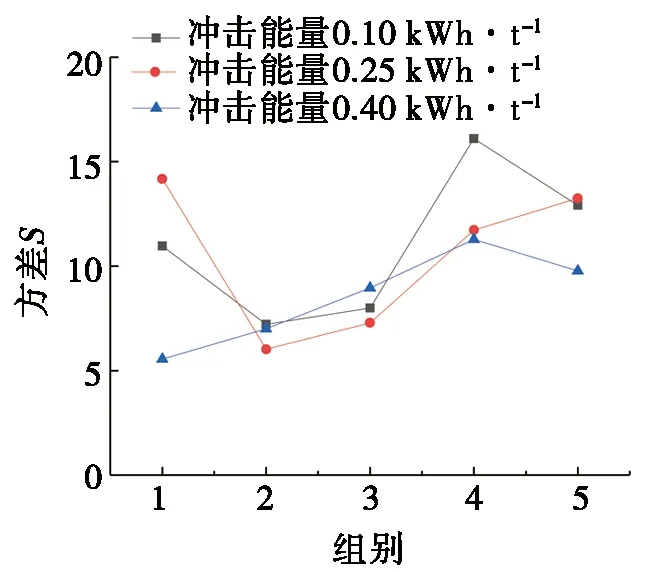
图5 不同组合下仿真与试验质量分数方差

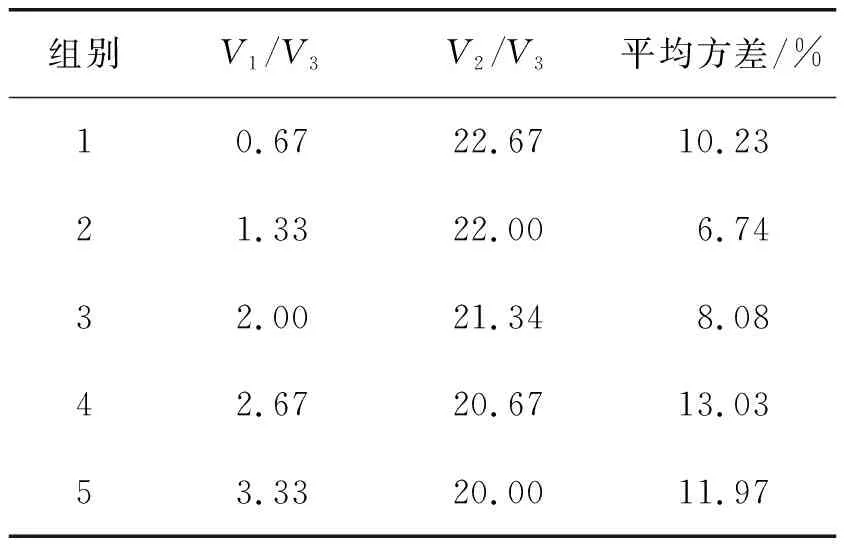
表5 不同组合下平均方差

4.3 基础颗粒组合的改进

方差分析表明，在基础颗粒组别2与组别3之间应存在更优的基础颗粒数量组合，因而可以在保持基础颗粒P3的数量不变的情况下，调整V2与V3的比例，实现基础颗粒数量的最优组合。以基础颗粒组别2与组别3的体积比均值(见表5)作为基础颗粒P2与P3体积比，即V2/V3=0.216 7，则可得到3种基础颗粒的个数分别为n1=3 200，n2=1 500，n3=1 500。以改进的基础颗粒数量组合进行建模及破碎仿真，得到不同冲击能量下粒度分布变化曲线,如图6所示。由图6可以看出：仿真结果和落重试验的一致性明显提高。

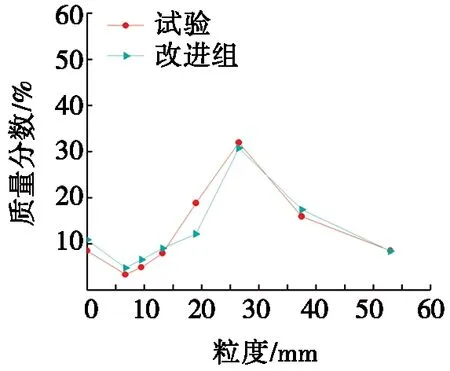
(a) 冲击能量E=0.10 kWh·t-1

比较5组数量组合与改进组仿真结果的方差(见表6)可以看出:当模型体积填充率不变时，不同的基础颗粒数量组合，其仿真结果有着明显的差异，亦即在构成颗粒黏结模型的基础颗粒中，每种基础颗粒的数量存在适宜的选择区间，在此区间内选取合适数量的基础颗粒，构成的颗粒黏结模型精度较高。

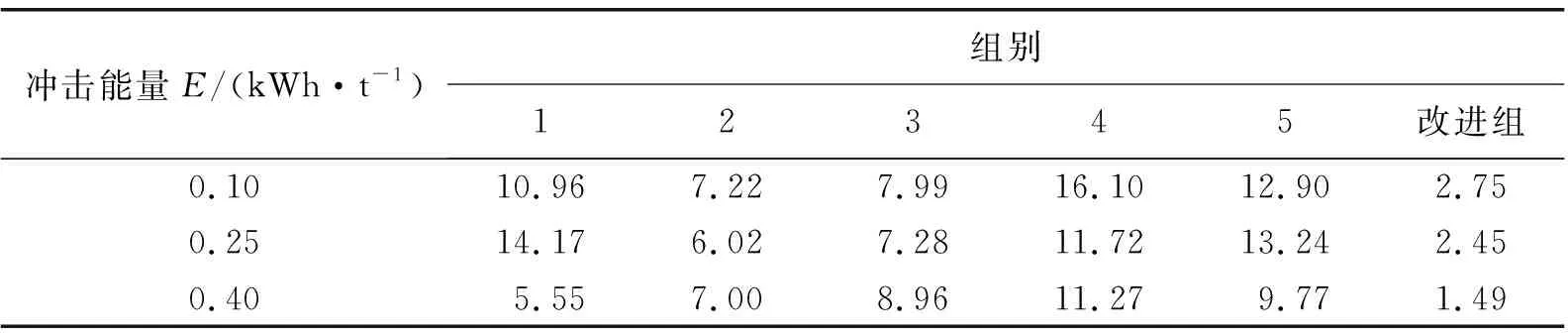
表6 仿真与试验的粒度分布方差

5 结束语

颗粒黏结模型中基础颗粒数量由模型的体积填充率和基础颗粒粒径种类决定。基础颗粒粒径种类数越多，基础颗粒总数变化范围越大，颗粒数量选取组合也越多。同一个矿石模型可以选取不同的基础颗粒数量组合进行建模，不同数量组合对破碎后粒度分布结果存在影响。选择合适的基础颗粒数量组合建模可以提高模型颗粒黏结特性精度。采用基础颗粒数量组合为1 mm颗粒3 200个、3 mm颗粒1 500个、5 mm颗粒1 500个对63～53 mm粒级金矿石进行黏结颗粒建模，能够较好地表征矿石破碎特性，仿真得到的金矿石破碎粒级分布与试验结果具有良好的一致性，为提高破碎模型精度研究提供了一定的依据。