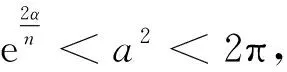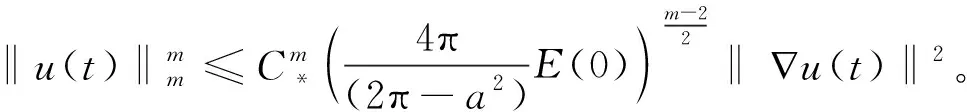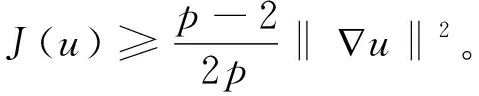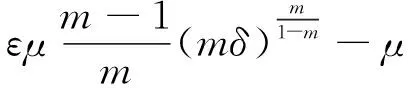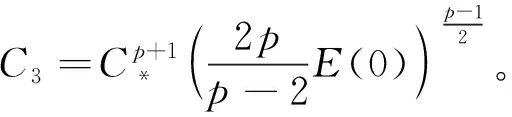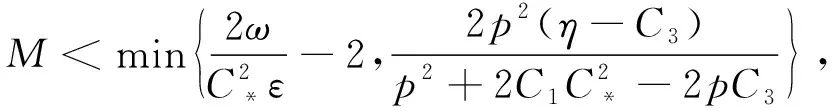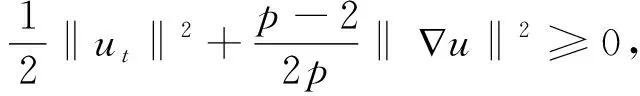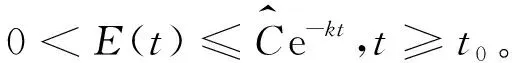具有阻尼和非线性对数源项的波方程能量衰减
2022-04-20武福敏郝江浩
武福敏,郝江浩
(山西大学 数学科学学院, 山西 太原 030006)
0 引言
本文研究如下波方程的初边值问题:
(1)
其中:Ω是Rn(n≥1)中的一个带有光滑边界∂Ω的有界区域,m≥2,p≥2,且
ω≥0,μ>-ωλ1,这里的λ1代表的是算子-Δ在齐次Dirichlet边界条件下的第一个特征值。
近年来,非线性阻尼和对数源项受到广泛的关注[1-2],尤其是对数源项,其在宇宙学、超对称场论、量子力学和核物理等领域起到很大的作用[3-4]。
文献[5-9]研究了一类带有非线性阻尼的波方程解的存在性、稳定性以及解在有限时间内爆破。
文献[10]研究了如下方程:
utt-Δu+u+ut=uln|u|2, (x,t)∈Ω×(0,∞),
(2)
用势阱方法证明了解的存在性。并通过构造Lyapunov泛函,证明了能量的指数衰减。文献[11-12]证明了带有对数源项的板方程解的全局存在和能量指数衰减。文献[13]考虑了如下方程:
utt-Δu-ωΔut+μut=uln|u|, (x,t)∈Ω×(0,∞),
(3)
证明了弱解的局部存在性、全局存在性、能量衰减以及解的爆破。文献[14-17]利用伽辽金法和势阱法证明了解的局部存在和稳定性。文献[18-20]证明了带有非线性对数源项的波方程解的稳定性以及在有限时间内解的爆破。
受文献[18-20]的启发,在文献[13]的基础上,本文研究带有非线性对数源项的波方程,利用伽辽金方法和势阱方法给出方程解的局部存在性以及能量衰减结果。
1 准备工作和主要结论
Lp(Ω)表示通常的Sobolev空间, 并且对于p∈[1,∞),赋予范数:
为方便记‖.‖2=‖.‖。存在嵌入常数C*使得:
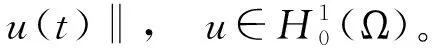
关于p给出如下假设条件:
定义1 称u是问题(1)的弱解,如果
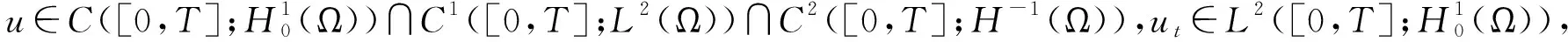
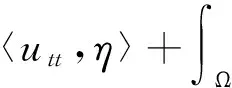
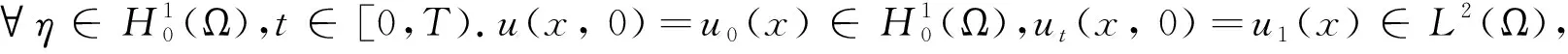
利用伽辽金方法以及压缩映射原理可得问题(1)弱解的存在性。这里省去证明过程。
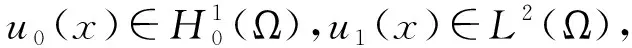
定义问题(1)的能量泛函如下:
(4)
令
(5)
(6)
定义稳定集W、不稳定集V和阱深d如下:
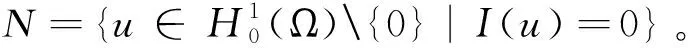
定理2 假设u0∈W,u1∈L2(Ω),假设(A)和E(0) 0 引理1 能量泛函E(t)是非增的,且满足: (7) 证明给问题(1)的第1个方程左右两边同时乘ut,并对x在Ω上积分,运用分部积分即可得到结果。引理1证毕。 引理2 假设有u0∈W,u1∈L2(Ω)和E(0) 证明设T是u(t)的最大存在时间,由引理1得: E(t)≤E(0) 即 下面用反证法证明,假设存在第一个时间点t0∈(0,T),使得I(u(t0))=0和I(u(t))>0对于0≤t 这与E(t) 引理3 假设有u0∈W,u1∈L2(Ω)和E(0) (8) 其中: 证明由引理2得,u(t)∈W,即I(u)>0。 由E(t)的定义知: 又根据E(t)与J(u)的关系以及E(t)≤E(0) (9) 根据对数Sobolev不等式: 得: (10) 情形2 当p>2时,由式(5)和式(6)知: 因此有: 同理得: 综上,得出结论,引理3证明完毕。 定理2的证明构造Lyapunov泛函, (11) 其中:ε>0是足够小的待定常数。通过计算知,存在两个依赖于ε的正常数β1和β2,使得: β1E(t)≤L(t)≤β2E(t), (12) 即E(t)和L(t)等价。将L(t)对t求导,得: (13) 利用Young不等式知,存在δ>0,有: (14) 将式(8)和式(14)代入式(13)得: (15) 因此,由E(t)的定义得: (16) 由Poincaré不等式得: (17) 将式(8)和式(17)代入式(16)得: (18) 由于 (19) (20) 令 L′(t)≤-MεE(t),t≥0。 由式(12),则存在常数C4>0,使得L′(t)≤-C4L(t)。进而积分可得,存在正常数k和C5,使得L(t)≤C5e-kt,t≥0。由引理2得,I(u)>0。则有: (21) 因此存在正常数C,使得0 引理4 假设有u0∈W,u1∈L2(Ω)和E(0)=d,则存在t0∈(0,T),使得: (22) 证明用反证法。假设: 则有‖ut‖=0,t∈[0,T)。因此,E(t)=J(t)≤E(0)=d。这与d的定义矛盾。引理4证毕。 引理5 假设有u0∈W,u1∈L2(Ω)和E(0)=d,则u(t)∈W。 证明运用引理4和反证法即可得到结论。证明过程与引理2类似,这里省略。引理5证毕。 引理6 假设有u0∈W,u1∈L2(Ω)和E(0)=d,则有: 其中: 证明证明过程与引理3类似,这里省去。引理6证毕。 定理3的证明由式(7)和式(22)得: (23) 根据引理5得,u(t0)∈W,即I(u(t0))>0或‖u(t0)‖=0成立。结合定理2,有: 0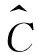
2 主要结论的证明