基于顶点范数的半脆弱盲水印算法

张国有, 崔 健, 王安红

(太原科技大学a.计算机科学与技术学院; b.电子信息工程学院, 太原 030024)

互联网的普及与快速发展使得三维模型数据信息的传播与使用不再受限,模型所有者的合法权益无法得到保障.同时三维模型数据的完整性缺乏有效的验证机制,而数字水印的提出为模型的版权保护和完整性验证提供了可行方法.目前, 数字水印研究主要针对图像[1-2]、音频[3-4]、视频[5-6]和文本[7-8]等多媒体数据.由于三维模型具有顶点数据无序以及表示方式与攻击类型复杂且多样化等特点,故关于三维模型的数字水印研究鲜见报道[9].根据水印对各类攻击的敏感度,可将数字水印分为鲁棒水印和脆弱水印.鲁棒水印在经过常规的信号处理操作和各类攻击后,仍能检测到水印的存在; 脆弱水印则对模型的各类修改操作敏感,主要用于内容认证等.然而,在实际应用中,鲁棒水印和脆弱水印无法较好地区分无害操作(如旋转、均匀缩放、平移或顶点重排序等)和恶意攻击(如噪声攻击、剪切或简化攻击等).半脆弱水印技术因对无害操作具有一定的鲁棒性且能够区分恶意攻击与无害操作而备受关注.Chou等[10]提出一种将水印嵌入到模型面片子集中的半脆弱水印算法,使其与相邻顶点保持预定义的关系,故除相似变换外的任何更改都会破坏标记面与相邻顶点之间的关系,从而影响水印的检测;徐涛等[11]提一种基于网格模型的半脆弱半盲水印算法,依赖预留的原始模型球面坐标映射方阵进行水印检测,其噪声和坐标量化检测值相对较高;Tsai等[12]提出一种具有较高嵌入率和区域篡改检测的半脆弱盲水印技术,该方法过于依赖输入模型的顶点精度,且在增加数据隐藏容量的同时易导致更大失真.为了扩展三维模型数字水印算法抵抗无害操作的种类, 提高水印对恶意攻击的敏感性并判断模型是否遭受恶意攻击, 本文拟提出一种基于顶点范数的多分区半脆弱盲水印算法(watermarking algorithm based on vertex norm, WABVN).通过坐标转换计算模型的顶点范数,构造水印嵌入基元并多分区冗余嵌入水印, 投票对比各分区水印检测出的内容,确定最终水印结果.

1 WABVN算法的嵌入与检测过程

三维网格模型一般采用顶点、由顶点围成的面片以及其他属性来表示,其中顶点可以笛卡尔坐标表示,面片通常是指由顶点围成的三角形或多边形.面片为三角形的三维网格模型可形式化表示为M=(V,F), 其中V={Vi∈R3|1≤i≤Nv}为模型所有顶点的集合,Vi=(xi,yi,zi|xi,yi,zi∈R)为模型的顶点,(xi,yi,zi)分别为模型顶点Vi的坐标,Nv为顶点数量;F={fi∈(vi1,vi2,vi3)|vi1,vi2,vi3∈V,1≤i≤Nf}为模型的面片集合,fi表示模型的第i个面片,vi1,vi2,vi3为组成三角形面片fi的顶点,Nf为三维网格模型中面片的数量.

WABVN算法的主要思想: 利用顶点范数的相对稳定特征, 实现对部分平移、旋转及顶点重排序等无害操作的鲁棒性;通过对顶点范数进行分区、排序和分段,实现对均匀缩放的鲁棒性以及恶意攻击的敏感性.在嵌入过程,将笛卡尔坐标系转为球坐标系计算模型的顶点范数,根据分区数量利用模型中范数的最大或最小值对模型进行分区,然后在各分区内分别嵌入相同的水印信息,最后还原至笛卡尔坐标下表示的模型数据,实现水印嵌入;在检测过程,首先对模型进行与嵌入过程相同的顶点范数计算,并实施区内分段和顶点范数统计操作,然后采用投票机制确认水印检测,最后得出水印信息.

1.1 水印嵌入

读取原始模型的数据和称作水印的数据,输出含水印信息的模型.在读取原始模型后计算模型的顶点范数,然后进行范数分区和排序,并做归一化处理;选取分区内的有效顶点,按水印位进行分组与数量统计,根据水印信息修改顶点的范数;通过逆处理将数据还原至空间坐标下,得到含水印信息的模型.WABVN算法的嵌入过程如图1所示.

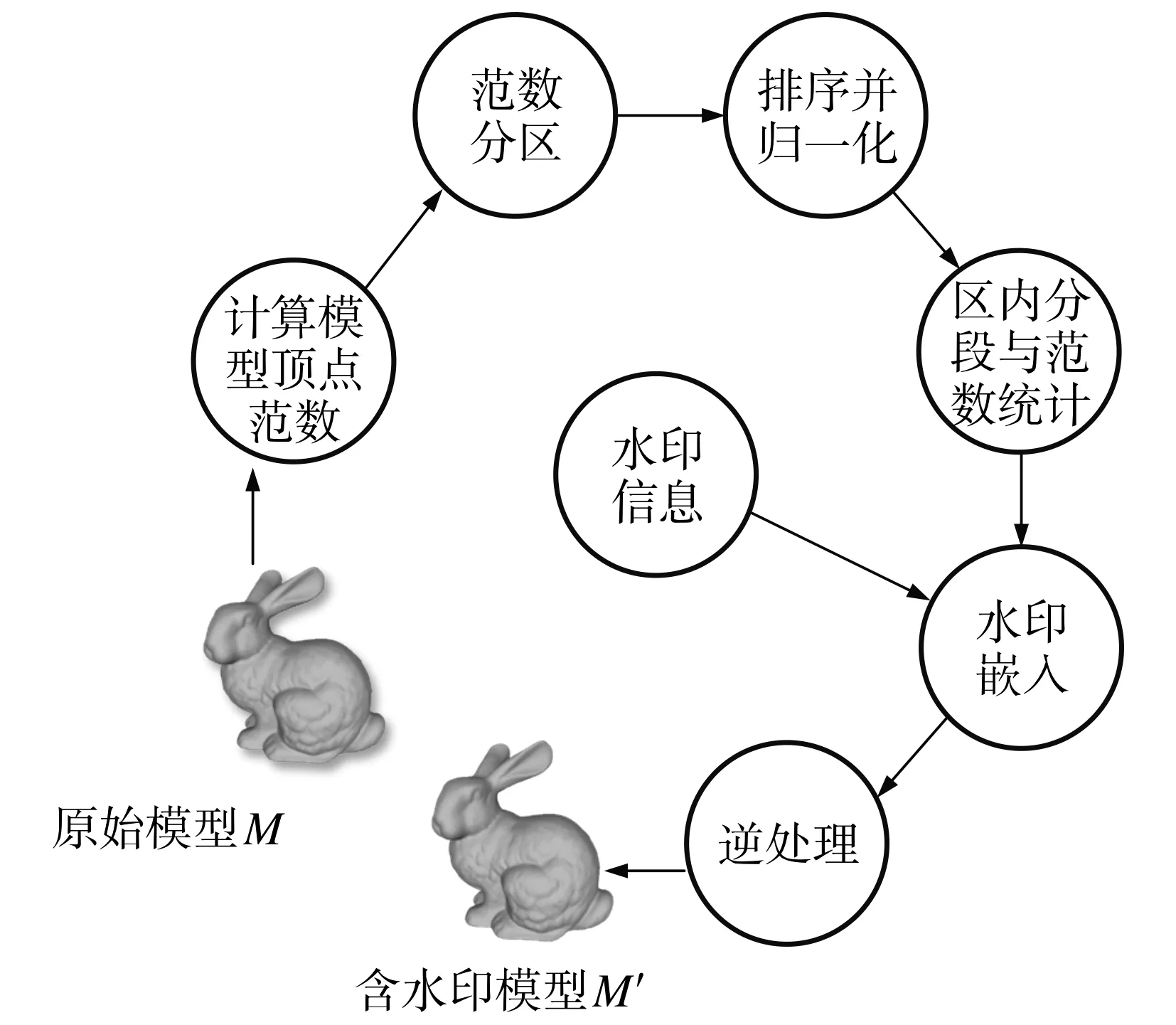
图1 半脆弱水印嵌入过程

1.1.1 计算模型范数

顶点范数即模型顶点到模型中心的距离.首先计算模型的中心

(1)

其中Vc(xc,yc,zc)为模型中心的坐标, 将其作为球坐标转换的原点坐标;然后根据公式

(2)

进行坐标转换, 将空间坐标转换为球面坐标, 其中(ρi,θi,φi)为模型顶点Vi在空间转换后的球面坐标,ρi∈R,θi∈[0,2π],φi∈[0,π],ρ,θ,φ分别为球面坐标下的顶点范数、顶点到中心点形成的经度和纬度.后续对ρ的修改不会改变θ和φ值, 因而降低了对模型的影响.

1.1.2 范数分区

对三维模型进行分区,可在不同的分区嵌入相同的水印内容,实现水印信息的冗余嵌入.根据模型中的最大范数、最小范数及分区个数对模型进行分区, 将所有顶点的范数分区到N个分区中(N为奇数):

(3)

其中Sn为模型的第n个范数分区,ρmax,ρmin分别为模型中最大范数和最小范数.

1.1.3 范数排序及归一化

对每个分区的范数进行归一化:

(4)

其中ρn,j为第n个分区中第j个顶点的范数,ρ′n,j为归一化后的顶点范数, maxρn, minρn分别为第n个分区中顶点范数的最大值和最小值,Mn为第n个分区中范数的个数.

1.1.4 区内分段与范数统计

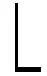
(5)

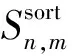
1.1.5 水印嵌入

通过公式

(6)

(7)

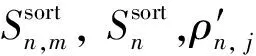
1.1.6 逆处理

分别根据式(8)(9)进行逆归一化处理，并将球面坐标转化为笛卡尔坐标:

(8)

(9)

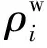
1.2 水印检测

WABVN算法的检测过程与水印嵌入过程大致相同,区别仅在于区内分段后通过检测和投票提取水印.由于检测过程无需原始模型参与,故属于一种盲水印算法.水印检测过程如图2所示.

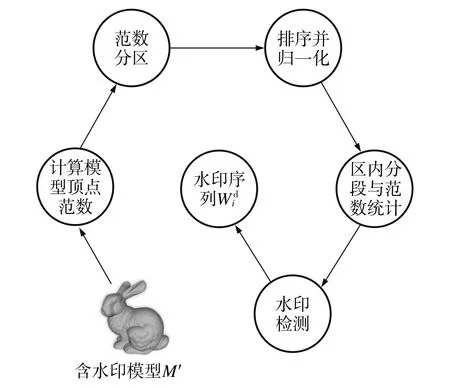
图2 半脆弱水印检测过程

在检测投票阶段,对每段内容进行如下判断:

(10)

得到当前分段内的数据.每个分区的水印检测结果为W′n=(W′n,1,W′n,2,W′n,3,…,W′n,i),W′n,i∈{0,1},1≤i≤Nw,1≤n≤N,其中W′n,i为第n个分区内第i位分段中检测出的水印内容.

将模型分为N个分区进行检测.对每个分区同一位水印内容投票得出该位正确的水印内容,投票方案如下:

(11)

其中count(W′n,i,1)表示统计不同分区之间第i位水印检测出内容为1的数量, 若不同分区同位检测出内容为1的数量比0的多,则认为该位水印内容应该为1.

多分区嵌入水印可增加冗余水印信息,提高模型对非恶意攻击的容错率和恶意攻击检测的敏感性.

2 算法测试与对比分析

2.1 测试环境与实验模型

本文算法的测试与实现在Visual Studio2013、MeshLab2016等环境下进行.采用法国里昂大学提供的Bunny、Hand和Dragon等三维网格模型[14],模型文件格式为“.off”或“.obj”,其顶点和面片的数量如表1所示.测试使用的水印内容是由伪随机函数产生的‘0’或‘1’组成的伪随机序列.水印序列可表示为W=(W1,W2,W3,…,Wi),Wi∈{0,1},1≤i≤Nw.嵌入水印长度Nw为64位,水印嵌入强度α=0.01,嵌入阈值D=1.5.

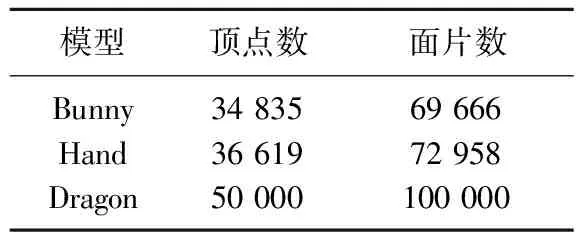
表1 模型信息

图3给出了3个模型的原始图像和含水印图像.由图3可见,仅从视觉感官角度无法辨别含水印模型与原始模型的差别.

图3 原始模型和含水印模型

2.2 评价指标

2.2.1 透明性评价

由于本文算法通过间接修改模型坐标的方式实现水印嵌入,故会导致模型存在一定程度的失真.现采用MeshLab2016中提供的豪斯多夫距离(Hausdorff, HD)和最大均方根(maximum root mean square, MRMS),对该失真进行水印透明性测评.

2.2.2 敏感性评价指标

选择相关系数(correlation coefficient,Corr)[15]作为本文水印算法敏感性的评价指标.相关系数的值域为[-1,1],其值大小可反映两个序列的相似程度.计算待检测水印内容与原始嵌入水印内容的相关系数

(12)

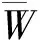
2.3 结果与分析

2.3.1 透明性评价

嵌入的水印信息是伪随机序列产生的64位和32位由{0,1}组成的水印序列, 每个模型测试5次并取其平均值.透明性测试结果如表2所示.

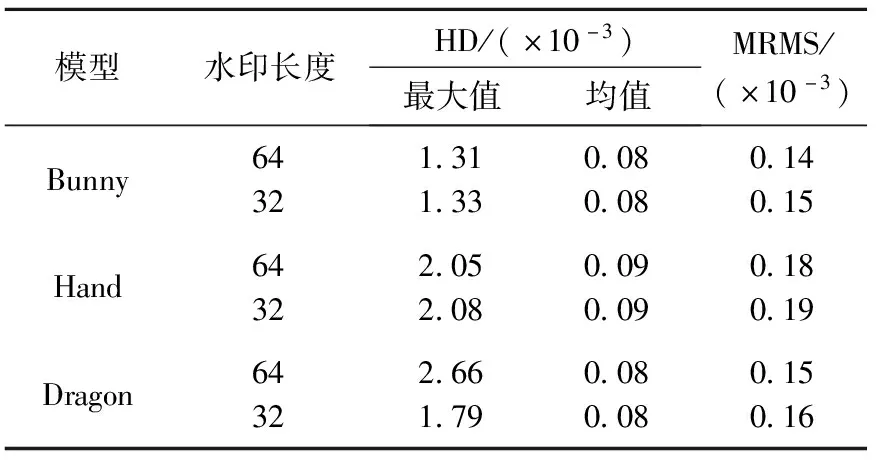
表2 透明性测试结果

2.3.2 敏感性测试

1)对于无害攻击的鲁棒性测试.由顶点范数定义可知,顶点范数不受平移或旋转的影响.顶点范数在分区后会根据范数的大小进行排序,虽然均匀缩放会改变范数的大小,但是范数之间的相对大小关系却不会发生改变,所以均匀缩放攻击不会影响水印检测.顶点重排序仅会改变顶点的顺序,而顶点坐标值不变,算法嵌入和检测不依赖于顶点顺序,故对于顶点重排序攻击可以完全抵抗.平移、旋转、均匀缩放、顶点重排序以及组合攻击的测试结果如表3所示.由表3可见,算法对于平移、旋转、均匀缩放及顶点重排序攻击,均可完全抵抗.

表3 水印对无害操作的鲁棒性测试结果

2)对于恶意攻击的敏感性测试.对Bunny、Hand、Dragon模型分别进行5组64位随机水印序列嵌入检测测试.测试采用随机噪声攻击,考虑噪声的随机性,故对每组噪声测试10次后统计其平均值.恶意攻击的5组测试平均结果如表4所示.由表4可见,算法对网络传输或使用过程中产生的小幅度非恶意噪声和量化影响是鲁棒的,对于恶意噪声和量化攻击则很敏感,相关系数快速下降.

表4 恶意攻击的敏感性结果

2.3.3 结果分析

在各类攻击类型下,本文算法与文献[11-12]方法的对比结果如表5所示.由表5可见,WABVN算法不仅可以容忍顶点重排序与其他无害操作的混合攻击,对恶意攻击的敏感程度更高,而且可以检测出更低幅度的噪声与量化攻击,同时也无需预先定义的数据信息和原始模型等相关数据便可实现水印内容的盲检测,具有更广的应用场景.

表5 与其他算法的对比结果