带有积分边值的Hadamard型分数阶微分包含解的存在性

杨丹丹

(淮阴师范学院数学与统计学院, 江苏 淮安 223300)

近年来, 由于分数阶微积分在自然科学领域的广泛应用, 关于分数阶微分方程和分数阶微分包含解的存在性结果大量涌现.Samet等[1]应用α-ψ-Ciric压缩映射的概念给出了此类映射的一些不动点结果; Mohammadi等[2]给出了α-ψ-Ciric广义多值映射的一些结果; Agarwal等[3]研究了两类分数阶微分包含.受上述研究启发, 本文拟研究带有积分边值的Hadamard型分数阶微分包含解的存在性, 与Caputo型和Riemman-Liouville型的分数阶微分包含问题不同, Hadamard型分数阶微分包含结果并不多见[4-7].

1 预备知识

本文研究带有积分边值条件的Hadamard型分数阶微分包含

(1)

定义3[4]Pompeiu-Hausdorff 测度Hd:P(X)×P(X)→R∪{∞}定义为Hd(A,B)=max{supa∈Ad(a,B),supb∈Bd(A,b)}, 其中d(a,B)=infb∈Bd(a,b),d(A,b)=infa∈Ad(a,b).

引理1[2]令(X,d)是一个完备的度量空间,α:X×X→[0,∞)是一个映射,ψ∈Ψ是一个严格增映射,T:X→Pcp(X)一个α-允许多值函数使得α(x,y)Hd(Tx,Ty)≤ψ(d(x,y))对于所有的x,y∈X成立, 存在x0∈X和x1∈Tx0满足α(x0,x1)≥1.若X满足条件Cα,则映射T存在一个不动点.

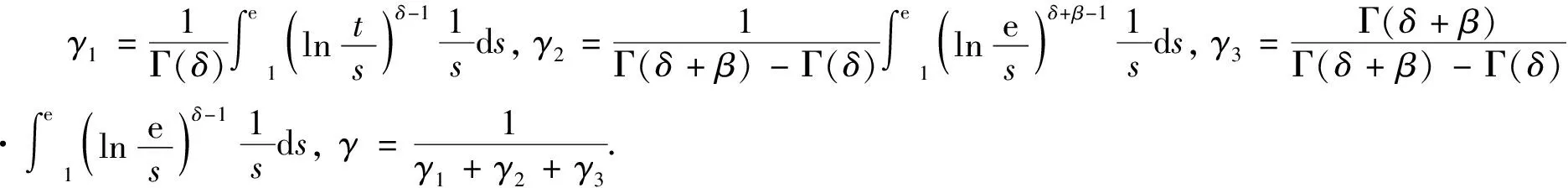
引理2[9]假设g∈C([1,e],R), 则问题

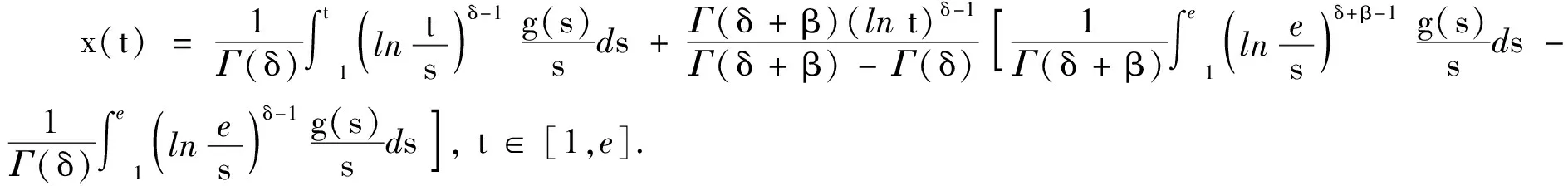
2 主要结果

假设条件为:

(H1)若F:[1,e]×R→Pcp(R)是一个可积有界的多值函数, 且F(·,x):[1,e]×R→P(R)对于x∈R是可测的.

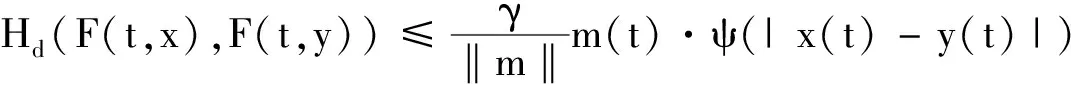
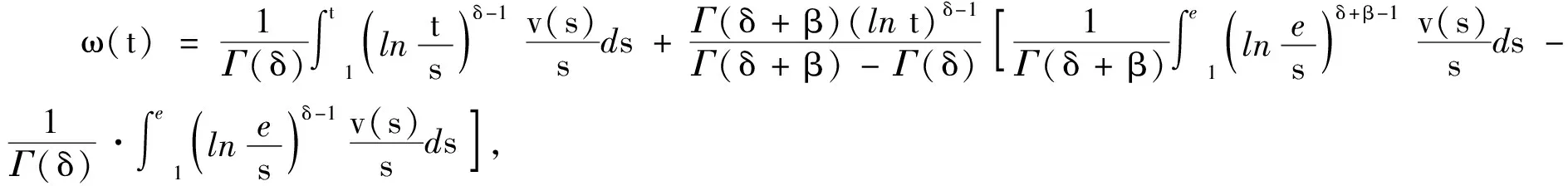
(H4)假设x0∈X,h∈ΩF(x0), 使得ξ(x0(t),h(t))≥0对所有的t∈J成立.

定理1若条件(H1)～(H4)成立, 则分数阶微分包含(1)存在一个解.

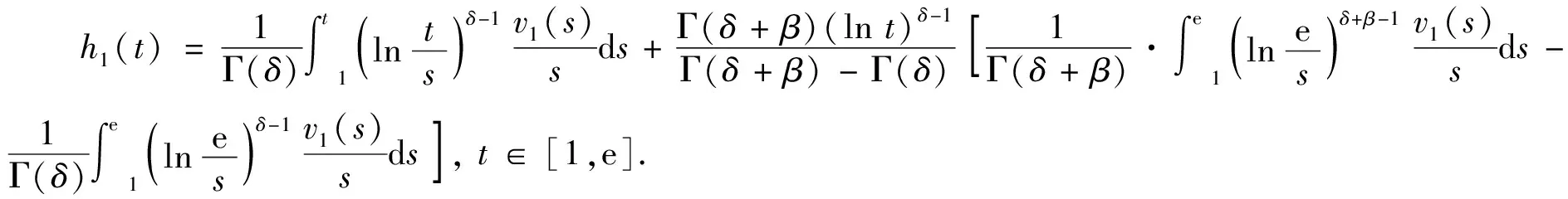
由多值映射ΩF是一个α-ψ压缩多值函数, 若y∈ΩF使得α(x,y)≥1, 有ξ(x(t),y(t))≥0, 存在z∈ΩF(y)使ξ(x(t),z(t))≥0, 则α(y,z)≥1, 故ΩF是α-允许的.若取x0∈X,y∈ΩF(x0), 使得ξ(x0(t),y(t))≥0, 这意味着α(x0,y)≥1.由引理1知, 存在x*∈X, 使得x*∈ΩF, 故x*是问题(1)的一个解.证毕.

本文应用α-ψ-Ciric 广义多值映射的不动点定理, 给出了带有积分边值的Hadamard型分数阶微分包含解的存在性,不同于文献的方法[10-15], 并将已有的单值结果[9]推广到多值.