基于反步法的不确定分数阶Shimizu-Morioka混沌系统的自适应无源同步

赵 飞, 周卫光, 郑永爱

(扬州大学信息工程学院, 江苏 扬州 225127)

混沌是复杂非线性动力系统的一种不规则或不确定现象, Shimizu-Morioka系统因包含了混沌动力学的许多特征而成为混沌领域研究的典型范例之一[1-2].近年来, Shimizu-Morioka系统的控制和同步实现方法主要有延迟反馈控制[3]、滑模控制[4]、主动控制[5]及自适应控制[6]等.但这些方法设计的控制器或过于复杂,或只适用于具有参数严格反馈形式的一类混沌系统, 在实际应用中备受限制.反步控制[7]作为自适应理论的重要分支之一, 其基本原理是将Lyapunov函数的选取与反馈控制器的设计相结合.该方法是为每个子系统构造Lyapunov函数并设计相应的虚拟控制律, 最终设计出系统的实际控制律, 从而保证整个闭环系统的稳定性.Ha等[8]提出一种自适应反步模糊控制方法,实现了输入饱和与外界干扰下的分数阶混沌系统的同步; Shukla等[9]基于自适应反步法实现了一类不确定分数阶混沌系统的控制与同步.无源控制[10]则利用无源理论对同步误差系统设计渐近稳定控制器,从而实现混沌系统的同步.无源控制具有明确的物理意义, 其控制结构简单且易于实现.Kuntanapreeda[11]、Sangpet[12]等提出一种具有时变增益的无源反馈控制方案,将同步误差动态转化为等效的无源系统, 实现了具有未知参数的混沌系统的自适应无源同步.本文拟结合反步控制、自适应控制和无源控制技术,针对参数不确定性的两分数阶Shimizu-Morioka混沌系统,提出一种自适应无源反步控制方法.

1 预备知识

定义Caputo分数阶微分

(1)

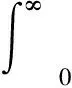
考虑分数阶系统

(2)

其中0<α<1,x∈Rn为状态变量,u∈Rm为输入向量,y∈Rm为输出向量,f(x)和g(x)为光滑向量场,h(x)为光滑映射, 且f(0)=h(0)=0.

假设系统(2)表示为如下形式:

(3)

其中(zT,yT)T∈Rn为系统的新坐标,z∈Rn-m;f(z)∈Rn-m;p(z,y)∈R(n-m)×m;b(z,y)∈Rm.对任意(z,y),a(z,y)是非奇异的.

定义1[13]如果存在一个正定Lyapunov函数V(z,y), 称之为存储函数或能量函数,满足对任意的t≥0且0<α<1有

(4)

则系统(3)是无源的.

定义2[13]如果存在一个正定Lyapunov函数V(z,y)和一个K类函数γ, 满足对任意的t≥0且0<α<1有

(5)

则系统(3)是严格无源的.

引理1[14]设

(6)

其中y1(t)∈Rn和y2(t)∈Rn具有连续的一阶导数,Q1∈Rn×n和Q2∈Rn×n为2个正定矩阵.若存在正定矩阵Q3∈Rn×n和常数h0>0, 使得对任意的0<α<1有

(7)

则‖y1(t)‖和‖y2(t)‖有界且y1(t)渐近趋于0, 即limt→+∞‖y1(t)‖=0.

引理2[15]设x(t)∈Rn是一个可微函数向量, 那么对于任意t≥0且0<α<1, 不等式

(8)

恒成立, 其中P∈Rn×n为一个n×n维常值正定矩阵.

2 主要结果

考虑如下不确定分数阶Shimizu-Morioka混沌系统:

(9)

其中x,y,z为状态变量, 分数阶0<α<1,a,b为不确定参数且a∈R,b∈R+.设z1=z,x1=x,x2=y, 则系统(9)可表示为

(10)

假设系统(10)为驱动系统, 则可控响应系统为

(11)

其中u∈R为控制输入.

定义3设X=(z1,x1,x2)T∈R3,Y=(z2,y1,y2)T∈R3分别是驱动系统(10)和响应系统(11)的状态向量, 若limt→+∞‖X(t)-Y(t)‖=0, 则称系统(10)与系统(11)渐近同步.

定义同步误差z0=z2-z1,e1=y1-x1,e2=y2-x2, 系统(10)(11)的同步误差系统为

(12)

显然,系统(10)与系统(11)的同步问题即转化为当t→+∞时同步误差系统(12)的零解稳定性问题.

定理1若设计虚拟控制律:

α1=-2x1z0-z0w1-w1,

(13)

以及自适应控制律:

(14)

(15)

证明 1)设e2为实际控制器,α1为虚拟控制器, 则子系统

(16)

2)系统(12)可转化为

(17)

3 数值模拟

当α=0.98,a=0.75,b=0.45,初始条件z1(0)=0,x1(0)=0.25,x2(0)=1时, 分数阶Shimizu-Morioka系统(10)呈现混沌现象.该系统的混沌吸引子如图1所示.

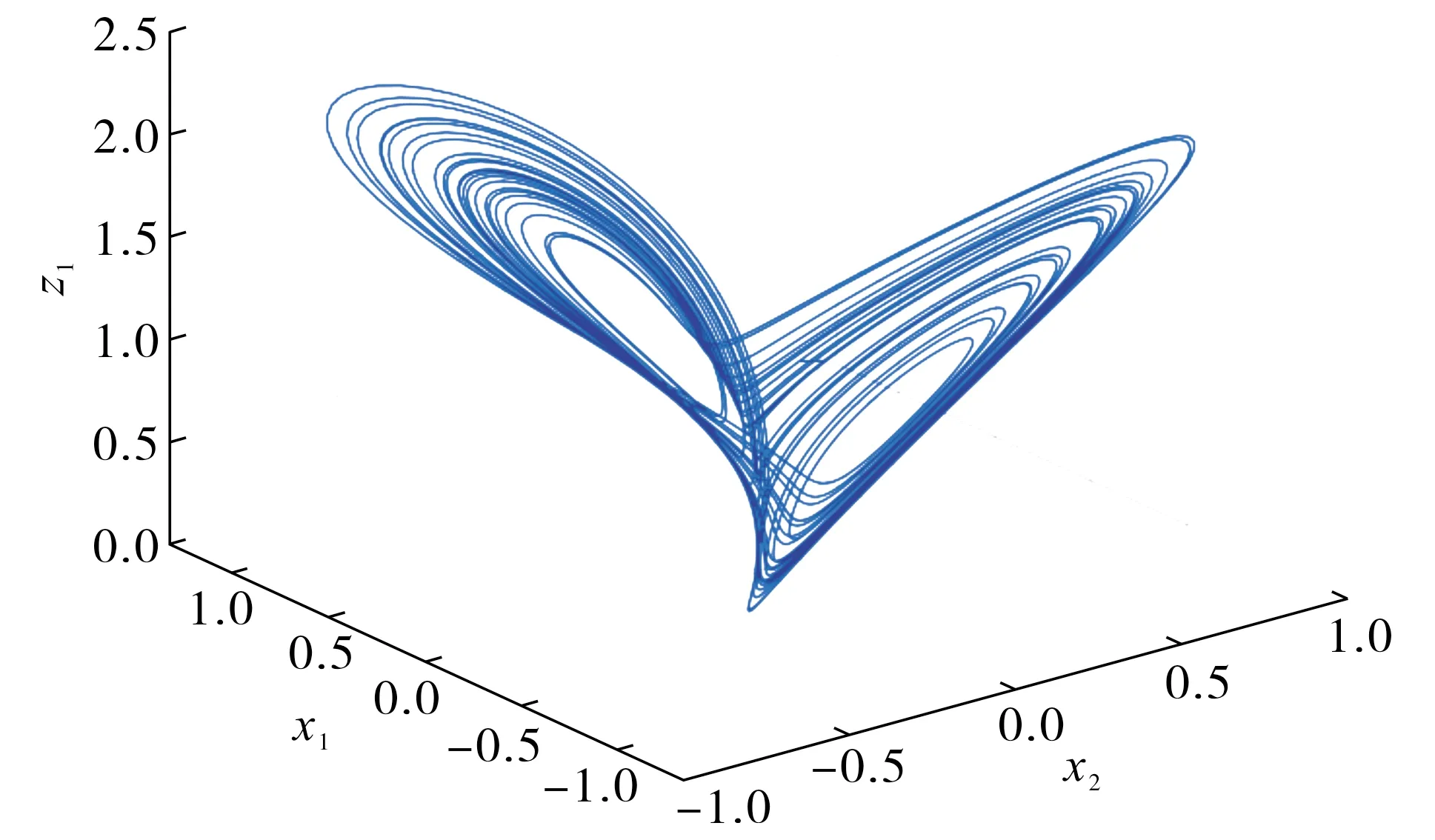
图1 分数阶Shimizu-Morioka混沌系统的吸引子

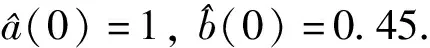
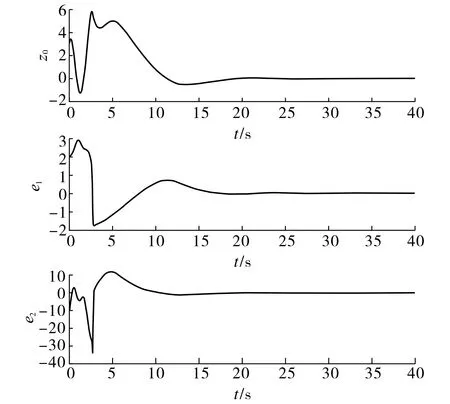
图2 系统同步误差曲线

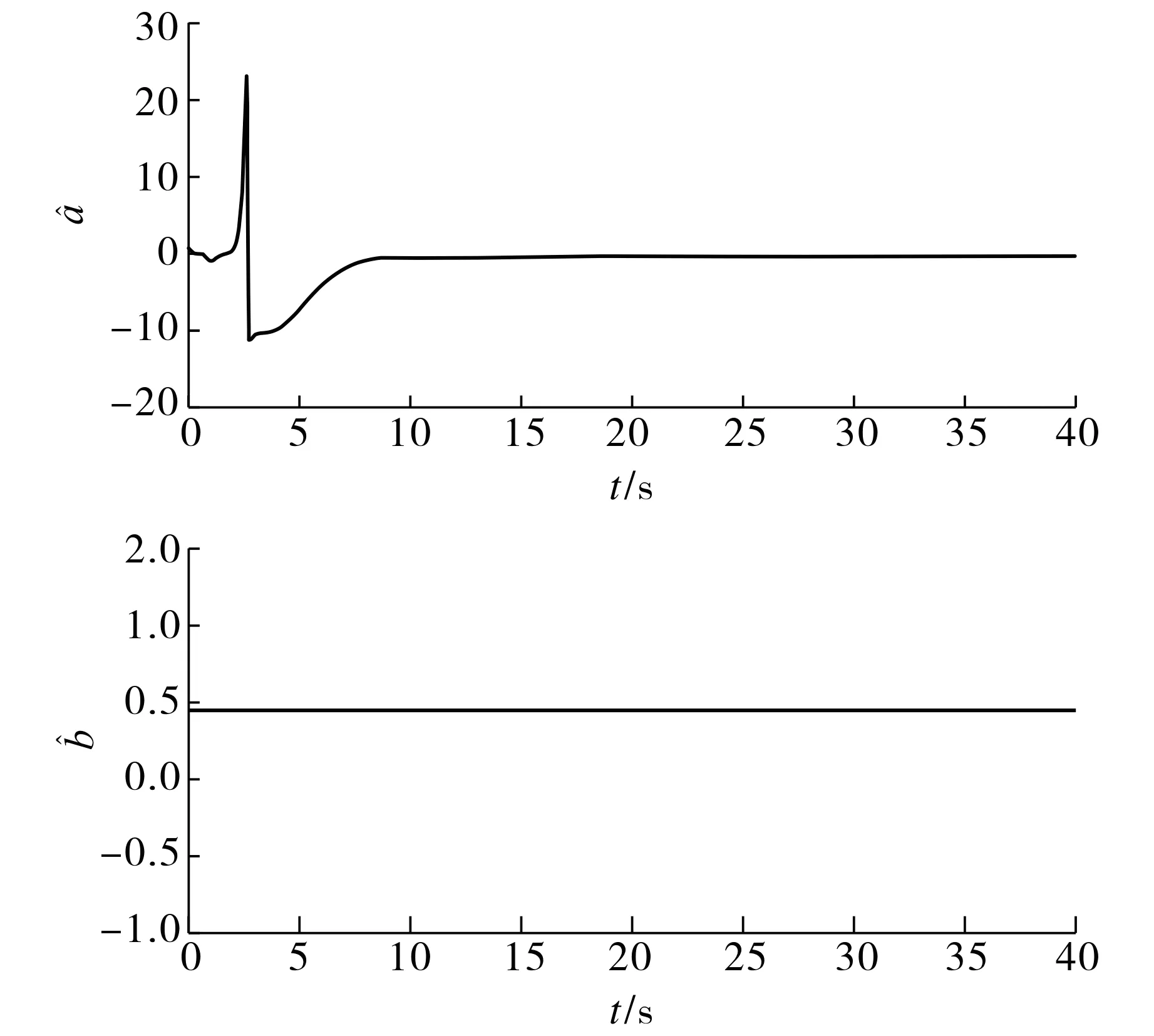
图3 系统参数a和b的估计曲线

4 结论

本文基于反步控制理论提出了一种不确定分数阶Shimizu-Morioka混沌系统的自适应无源同步控制方法.利用反步控制的递推过程, 独立设计了子系统的能量函数和自适应虚拟控制律, 然后设计出整个系统实际的自适应控制律, 有效实现了对分数阶Shimizu-Morioka混沌系统同步的自适应无源反步控制.