输入时滞下异质调和振子网络的同步研究

张伟业, 刘怡文, 付求耐, 王正新,c*, 韩欣利

(南京邮电大学a.理学院; b.通信与信息工程学院; c.江苏省物联网智能机器人工程实验室, 南京 210023)

近年来, 复杂网络因在科学和工程中得到广泛的应用而受到越来越多的关注[1-3].复杂网络中有许多有趣而重要的群集现象,如自组织、同步和时空混沌等,在这些现象中,同步现象已在不同领域得到了深入研究.众所周知,信息传输过程中不可避免地存在时间延迟现象,这会对系统的行为产生巨大影响[4].因而, 时滞系统的动力学研究吸引了广大研究者的关注,特别是关于稳定性和同步方面的研究[5-6].早期, 对于调和振子网络的同步研究大多基于同质网络[7],而实际情况中调和振子网络中各振子的运动参数难以保证完全相同,因此异质调和振子网络更为常见.然而,异质网络通常难以自己实现同步,因而通常研究异质网络的拟同步[8].为了实现拟同步,需要设计和应用外部控制.近年来,已经有很多学者针对网络同步问题考虑了多种控制策略.马垚等[9]研究了一类具有未知参数的时滞混沌系统的广义复杂修正混合函数投影同步控制问题,建立了复杂网络系统指数同步准则,获得了复杂网络系统间歇同步的控制策略; Zhang等[10]研究了非线性耦合时滞神经网络的聚类同步问题,基于李雅普诺夫稳定性理论和牵制控制策略,给出了聚类同步的准则; Zhao等[11]通过自适应周期性间歇牵制控制,在两个具有时延的复杂网络之间实现同步.对于具有大量节点的网络,不可能对所有节点施加控制,此时可通过引入领导者来牵制部分节点.金彦亮等[12]研究了当振子受到外界领导者节点驱动时系统的同步行为; Liu等[13]运用牵制控制策略和M矩阵理论研究了耦合时滞神经网络的二分同步问题; Ding等[14]设计一种基于脉冲控制的分布式控制器,实现了一类具有时变时滞和随机干扰的非线性耦合复杂网络的指数同步;蒲浩等研究了变时滞随机竞争型神经网络在固定时间的控制同步问题,运用李雅普诺夫稳定性理论, 在p-范数下得到了新的固定时间同步的充分条件[15], 进一步通过构造一个恰当的反馈控制器得到一类具有反应扩散项忆阻Cohen-Grossberg型神经网络在固定时间内同步的充分条件[16].受上述研究的启发,本文旨在通过构造一种牵制控制策略,探讨一类含时滞的异质调和振子网络的拟同步问题,其中复杂网络由一个领导者调和振子与许多跟随者调和振子组成,拟通过使用Lyapunov稳定性方法,给出含时滞时异质调和振子网络实现拟同步的充分性判据.

1 基本假设

假设1从领导者调和振子到每个跟随者调和振子至少存在一条有向路径.

假设2领导者调和振子的状态是有界的.

2 模型建立

2.1 异质调和振子系统

由n+1个不同调和振子构成的时滞异质网络系统为

(1)

其中i=0,1,2,…,n,i=0为领导者调和振子;xi(t),vi(t)∈R分别表示第i个调和振子的位移状态和速度状态;ωi为第i个调和振子的角频率;ui∈R表示第i个调和振子的控制协议, 且u0=0;τ为系统的输入时滞.

2.2 牵制控制协议

在网络系统(1)中, 设计牵制控制协议为

(2)

其中常数c>0是系统的耦合强度;aij是边eji的权值;di表示第i个调和振子的牵制控制强度, 当且仅当该调和振子被牵制控制时,di>0, 否则di=0.不失一般性, 不妨设该系统的前k个调和振子被牵制控制.

2.3 误差系统

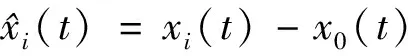
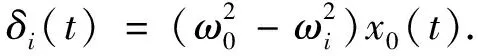
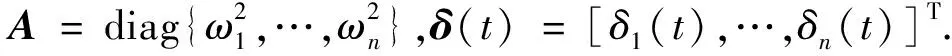
(3)

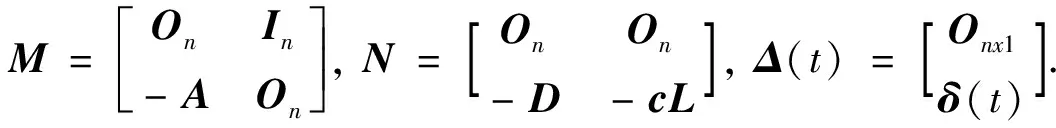
定义1[8]如果存在一个充分大的T, 使得当t>T时,‖xi(t)-x0(t)‖和‖vi(t)-v0(t)‖保持有界, 那么就称异质网络实现了拟同步.

构造Lyapunov-Krasovskii泛函

V(t)=V1(t)+V2(t)+V3(t),

(4)

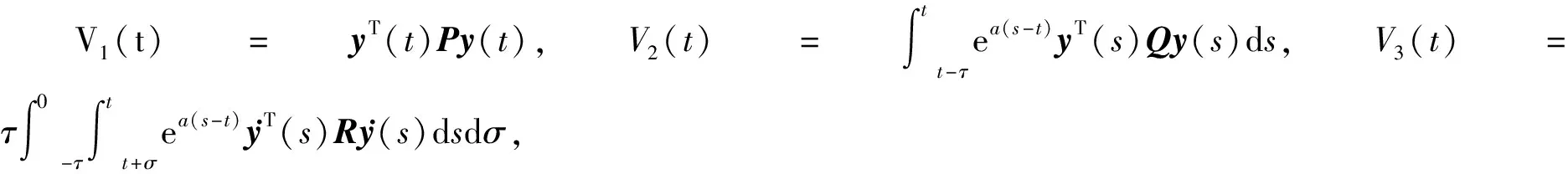
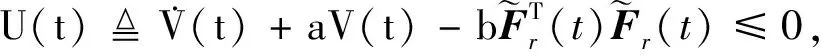
3 拟同步的充分判据

定理1若假设1和假设2成立, 且存在常数a>0,b>0,τ>0和矩阵P>0,Q>0,R>0,任意矩阵S,T使

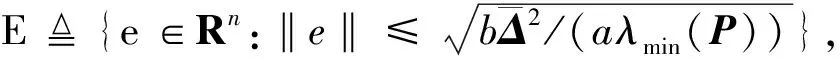
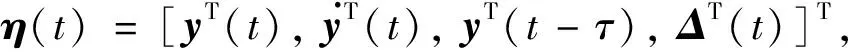
(5)

从而, 要使U(t)<0, 即二次型ηT(t)Φ0η(t)负定, 故矩阵Φ0须满足二次型负定的必要条件: 对角线元素均小于零.易知, 该矩阵的对角线元素除了第二行第二列的元素以外,均有可能小于零, 而第二行第二列的元素一定大于零, 故要通过恒等变形, 构造一个新的矩阵Φ, 使其满足必要条件.

从而U(t)≤ζ(t)+aV1(t)-bΔT(t)Δ(t)=ηT(t)Φη(t).根据引理1及条件P>0,Q>0,R>0可得U(t)<0, 即系统能实现拟同步.

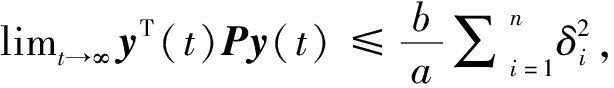
注1LMI:Φ<0可分三步进行求解: ① 给定常数a>0,b>0,τ>0; ② 通过MATLAB中LMI工具箱首先给出LMI变元P,Q,R,S,T矩阵, 并表示出矩阵不等式, 求解得到P,Q,R,S,T矩阵; ③ 如果LMI有解, 则增大τ, 并返回第一步继续求解, 以取得时滞的上界; 如果LMI无解, 则减小τ, 并返回第一步继续求解.

4 数值算例

考虑由8个异质调和振子和领导者振子组成的网络系统, 其拓扑结构如图1所示.其中节点为领导者振子.选取:A=0.5diag(1.10,1.15,1.20,1.25,1.30,1.35,1.40,1.45),c=2,d1=29,D=0.5diag(d1,0,0,0,0,0,0,0),τ=0.01,a=0.01,b=10.通过求解LMI可得, 存在P,Q,R,S,T使λmax(Φ)=-0.002 038, 即Φ矩阵负定, 满足引理1的条件.

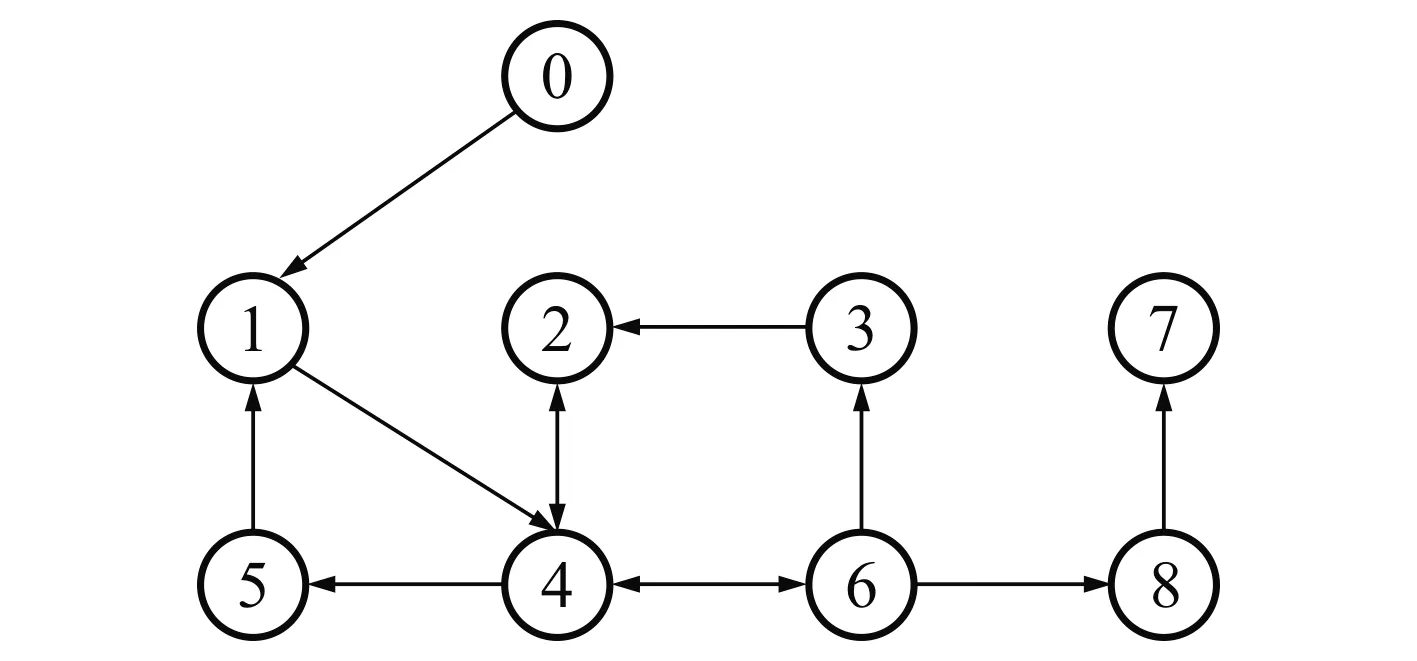
图1 网络拓扑结构

设领导者振子的初始值为[x0(t),v0(t)]T=[5,0.5]T,t∈[-τ,0].当t∈[-τ,0]时, 从[0,5]随机选取跟随者振子的初始位移,从[-5,5]随机选取跟随者振子的初始速度.系统中的8个跟随者振子和1个领导者振子运动的位移和速度状态轨迹分别如图2和图3所示.从图2～3可以看出,谐振子网络系统实现了拟同步.

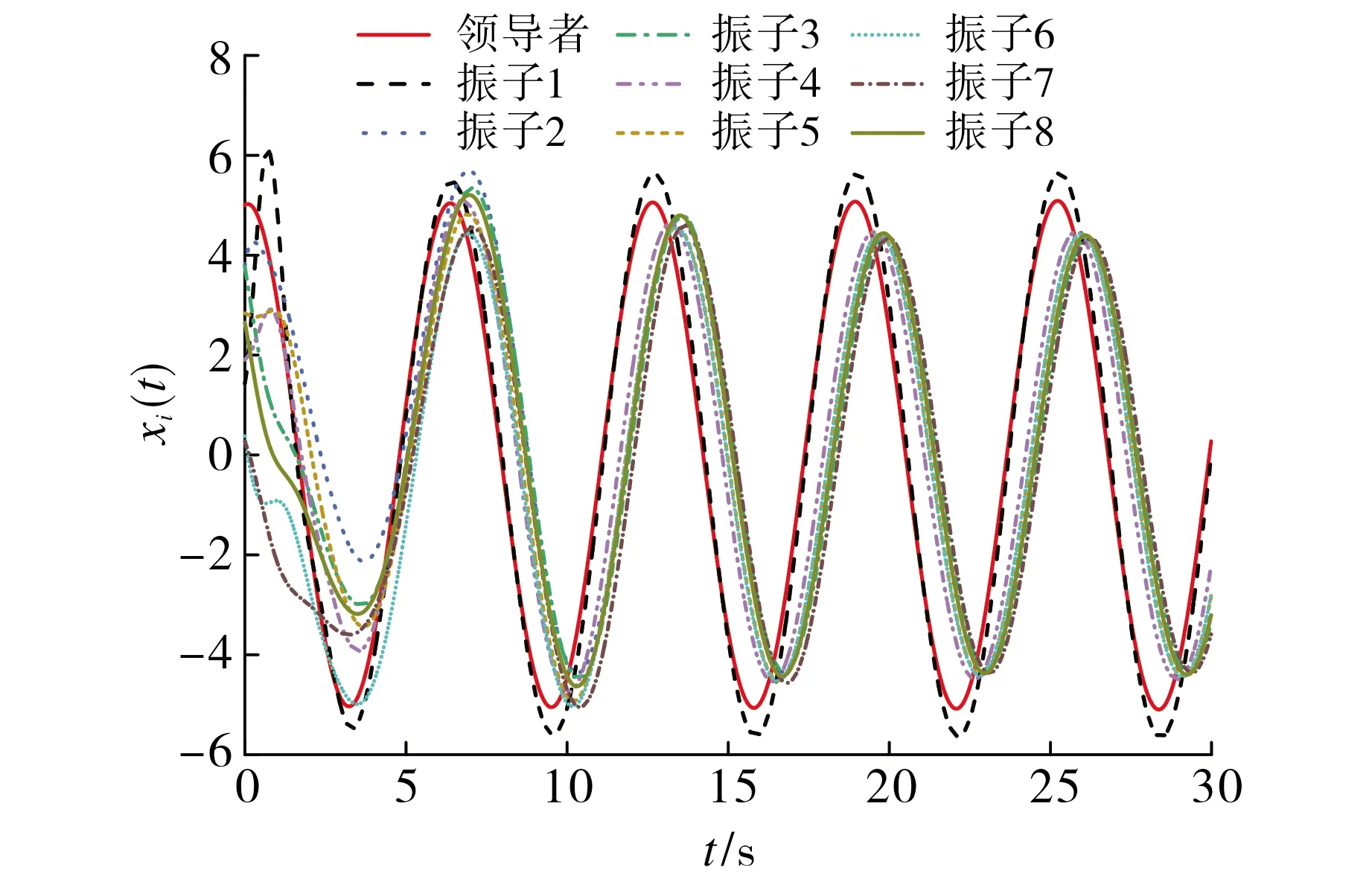
图2 谐振子的位移状态轨迹图

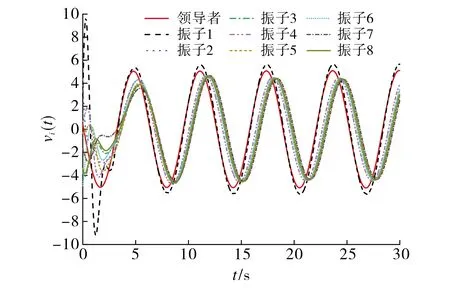
图3 谐振子的速度状态轨迹图

本文创新之处在于针对调和振子网络考虑更为常见的异质网络,同时针对信息传输过程中不可避免的时滞问题考虑了输入时滞.相较于部分已有文献,本文的控制协议仅需要更少的信息就能实现拟同步,即耦合部分仅需要速度信息,牵制部分仅需要位移信息.