复合材料圆筒中的应力波和破坏

杨宇宙，徐亚栋，陈龙淼

(南京理工大学 机械工程学院，江苏 南京 210094)

当一个幅值足够大的应力波通过结构体时，有可能导致结构的破坏或加速结构中起始裂纹的扩展。动态载荷导致的破坏机理不同于静载，这是因为：应力波的速度一般远大于裂纹的扩展速度，随着应力波的快速通过，裂纹不会及时扩展；瞬时载荷条件下结构的变形具有时间相关性；加载速度的大小对材料韧性破坏和强度的测量影响很大，对于韧性材料，如增强聚合物复合材料，得到的结果可能偏向脆性，所以静载条件下得到的破坏韧性和强度[1-2]不适用于动态情况。

当压力的移动接近临界传播速度时，圆筒中就会产生共振现象。共振导致圆筒中压力前缘处的应变具有非常高的幅值和频率。Donadon等[3]和McCartney[4]研究了移动压力载荷作用下圆筒的共振效应。最近Abdewi等[5]研究了炮管中弯曲波的动态响应。Tzeng[6]将研究扩展到带金属内衬的纤维增强复合材料圆筒的动态应变的影响。以上研究成果适用于设计炮管和高压管道系统，及其减重设计。

考虑应力波的影响对于设计高性能、质量轻的复合圆筒是十分重要的。压力前缘沿着圆筒移动时出现的压力不连续会引起薄壁圆筒结构的局部弯曲[7]，而质量的减轻会降低动载作用下结构的刚度和惯性[8]，因此在某种程度上减重设计会放大或缩小压力波造成的动态响应。弯曲变形会引起很高的轴向和横向切应力，其幅值的大小十分关键，因为复合材料的剪切强度要低于金属的剪切强度[9]。

从设计安全的方面考虑，动态响应的分析很重要，尤其是复合材料层和金属内衬之间界面处的响应分析，因为动态条件下的应力应变水平高于静态条件下的数倍，且层合结构和不同材料界面间结合处的刚强度最为薄弱，其剪切属性和拉脱强度相对较低，常导致该处的起始脱粘分层。另外，动态周期应变会加快复合材料中裂纹的扩展，导致复合圆筒的最终破坏。因此，笔者仿真分析了带金属内衬复合材料圆筒在移动内压载荷作用下的动态响应，及不同的弹丸初速对结构动态响应的影响，用于研究应力波传播对复合圆筒造成的损伤行为。

1 复合圆筒的动态响应

考虑一个半径为R的正交各向异性薄壁圆筒受到轴对称径向压力载荷作用。其几何结构、坐标系和边界条件如图1所示。

移动内压载荷作用下该模型的控制方程可用Heaviside阶梯函数表示为

P[1-H(x-vt)],

(1)

式中：w为径向位移，取决于时间t和轴向坐标x；m为质量；ρ为壳的材料密度；h为壳的厚度；P为内压；假设压力前缘的速度v为常数；μxθ和μθx分别为复合材料的轴向和周向泊松比。

结构的轴向和周向弯曲刚度表达式分别为

(2)

(3)

式中,Ex和Eθ为有效弹性模量。

对于正交层合结构的复合材料圆筒，沿轴向和周向的壳弯曲刚度是不同的，可通过轴向层到周向层的比例得到。式(1)中的加载函数P[1-H(x-vt)]表示内压前缘以不变的速度v沿着轴向方向移动，H(x-vt)为Heaviside阶梯函数。因此有

(4)

Tzeng[6]给出了正交各向异性复合圆筒的临界速度的表达式：

(5)

式(5)表明移动压载作用下正交异性圆筒临界速度与筒几何特征、密度、泊松比和弹性模量有关。从设计的角度讲，动载条件作用下圆筒的构建应选择高刚度、质量轻的材料，但是式(5)表明在其他参数不变的情况下，压力波的速度越大，需要结构的壁厚越大。同时，也显示出轴向和周向的弹性模量都会对临界速度产生影响。因此可以通过改变复合材料圆筒中各层板的参数进行设计优化。

对于各向同性区域，式(1)～(5)可以得到很大的简化，因为轴向和周向的材料属性均相同。此时的临界速度可表示为

(6)

2 破坏和能量密度积分

假设结构中复合材料层和金属内衬层界面处存在一个裂纹，如图2所示。

接近裂纹尖端的应变场很难定义，尤其是在这种含各向异性复合材料的双材料系统中。假设界面处的裂纹是轴对称的，可通过建立二维模型对裂纹和远场进行分析。文献[10]提出一种近似方法，被称为J积分，回避了求解边值问题的复杂性。围绕裂纹尖端的路径J的积分可定义为

(7)

式中：T沿路径的拉矢量；ds为沿Γ的单元弧长；u代表位移矢量；ω为应变能密度，可定义为

(8)

忽略该时刻与材料内部运动有关的动能，但是其影响在式(7)中表现出来。Rice指出，J积分在弹性条件下很明显等同于应变能释放率，可以表示为

(9)

式中：Q代表弹性体的势能；a为裂纹长度；G为源于3种破坏模式的总应变能释放率，应变能释放率同应力强度的关系式为

(10)

式中，KⅠ、KⅡ和KⅢ分别为与3种破坏模式有关的应力强度因子。

通过在有限元积分过程中导入应变能，可详细模拟出含微裂纹复合圆筒的破坏状态。围绕裂纹尖端的应力应变场可以通过瞬态分析计算获得，沿着指定路径，可逐单元计算出应变能密度及其积分值。结果同实验值进行对比，并被用作设计和制造参数。

3 有限元模拟动态响应

3.1 建模求解

本文研究的结构有限元模型包括复合材料圆筒和金属弹丸两部分，如图3所示，圆筒结构内径r0为61 mm，外径rN为84 mm，轴向长度为1 m，由4层等厚度碳纤维增强树脂基复合材料层和金属内衬层组成，复合材料层每层厚度为1 mm，沿径向堆积，各层堆积顺序由内而外依次为0°，53°，-53°和90°。

网格划分方案为，金属内衬部分采用六面体实体单元，复合材料部分采用四边形壳单元。弹丸最大外径为62 mm。由于主要研究对象为复合圆筒，因此对于次要部分金属弹丸，采用精度稍低的四面体单元进行划分网格。

结构中，金属材料采用Ni3钢，复合材料采用T300/Epoxy，金属材料和复合材料的基本材料参数如表1、2所示[6]。

表1 材料强度特性表

表2 材料物理特性表

3.2 载荷边界条件

对复合圆筒的左端面施加轴向位移边界约束，在复合厚壁圆筒的内表面施加冲击压力载荷，该载荷由弹丸的挤进产生，在弹丸底部施加一个随时间变化的均布载荷，如图4所示。当时间达到2.724 74 ms时，载荷达到最大值388.110 61 MPa。

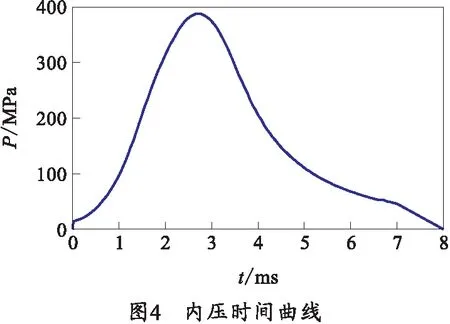
分别赋予弹丸两种不同的平均速度，分别为230 m/s和430 m/s，对动态响应结果进行对比分析。两种情况下弹丸通过圆筒的时间分别为3.2 ms和2.4 ms。为了精确获得圆筒的动态响应，计算执行时选取时间增量为1 μs，因此每次分析大约需要3 500～4 000个时间步。该时间间隔允许压力沿着滑块移动后的单元表面缓慢爬升至最大值。这意味着压力边界条件突然作用于单元表面所引起的人为数值应力振荡能够最小化，这样，这些数值振荡不至于反过来影响结果。

3.3 结果分析

在两种不同初速情况下，弹丸移动2.16 ms时结构的应力云图如图5、6所示。

从图中可清晰地看到圆筒壁中的变形情况和应力振荡。最大应力和位移出现在压力前缘、弹丸同圆筒挤压接触的位置，并从压力前缘沿着轴向两边减小。结构变形图的数据显示方法能够直观地显示出位移、应力和应变场的空间变化。但是该方法与观察视角有关，且不能详细描述结构内具体某一节点或单元随时间的动态响应状态。这就需要在复合圆筒上选一固定点，观察位移、应力随着压力前缘接近和通过该点时的变化。

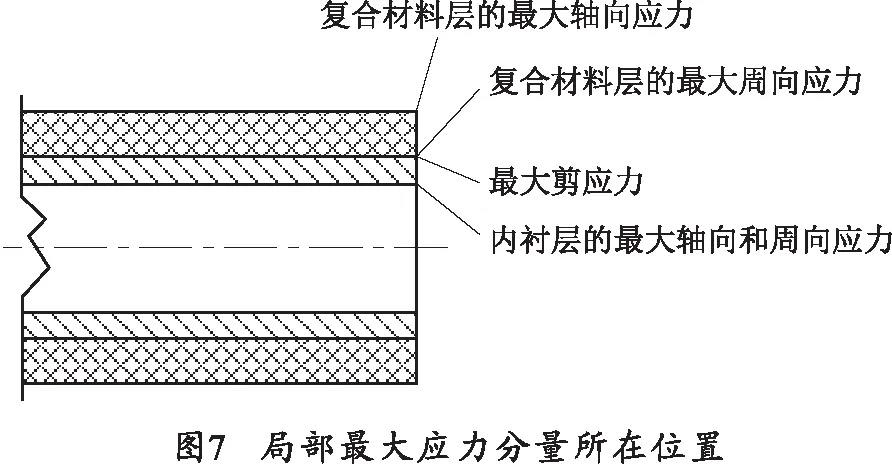
复合圆筒中位移和应力分量最大值所处径向位置如图7所示。由于圆筒遭受内压载荷作用，所以周向应力最大值发生在内衬层的内表面。当压力前缘通过一个给定的轴向位置时，筒壁中将发生局部轴对称弯曲。最大轴向应力将产生在内衬的内表面和复合材料层的最外层表面。与弯曲有关的最大剪应力位于横截面的中轴处。相应的复合材料层板横向临界切应力产生于内衬和复合材料层界面的附近。

复合圆筒中复合材料层动能随时间的演化曲线如图8所示。

在弹丸接触圆筒瞬间，圆筒受到冲击，复合材料层开始产生动能。随着弹丸的深入，动能不断累加，直至弹丸从另一端冲出，动能迅速降到很小值，并在该值附近进行振荡衰减。对比两条曲线可发现：弹丸速度越大对圆筒所带来的动态响应也越大，相应的各部分的动能峰值也越大；弹丸的速度越大通过圆筒的时间就越短，圆筒的响应时间也越短，能量转化就更剧烈，对圆筒的安全使用造成不利影响。

复合材料最内层的径向位移随时间演化曲线如图9所示，表明：弹丸速度不同，情况1(指弹丸冲击平均速度为230 m/s)和情况2(指弹丸冲击平均速度为430 m/s)中复合材料最内层的径向位移峰值出现的时间有显著不同，但是大小差别不大。在压力前缘抵达之前，圆筒中这些观测点基本上没有什么变化，只产生一些细微振荡和由压力前缘移动所产生的代表性的应力振荡。显见，当压力前缘通过的同时，径向位移快速增加，但是，如果速度很低的话，产生的位移和应力就会接近于静态压力载荷作用下的结果。理论上对于线弹性行为，圆筒的振荡响应会一直持续下去，事实上却是不断减弱，这是因为材料内部的衰减和屈服之后的变形起到了阻滞作用。当弹丸远离该轴向位置时，径向位移趋于稳定值，可通过对受压载作用圆筒进行静力分析得到。情况2中的速度高于临界速度，此时径向位移的峰值实际上小于将压力前缘的速度从230 m/s增加到430 m/s时得到的峰值，尽管压力前缘在某些轴向位置已经超过了临界速度。这可能导致在这些位置处产生共振，同时径向位移的峰值至少是静力分析得到的1.2倍。

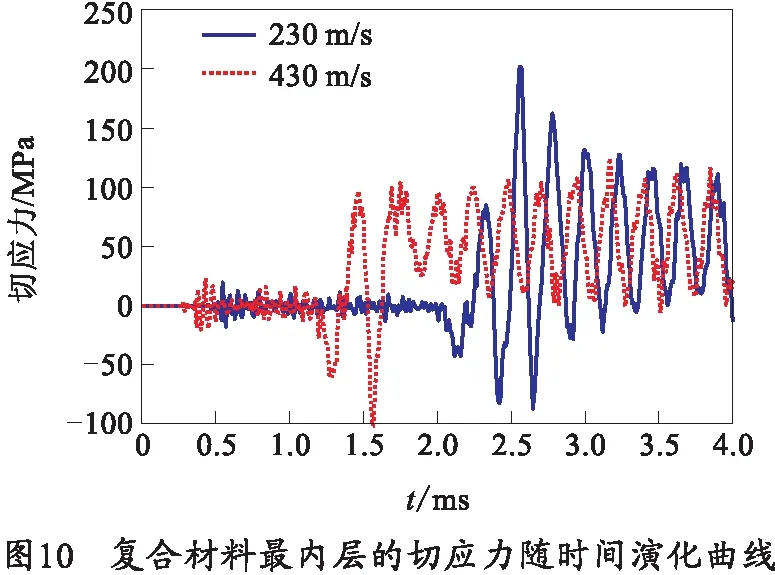
两种速度情况下，复合材料最内层的切应力随时间的变化关系如图10所示，可以明显看出弹丸到达观测点之前，应力只在0附近轻微振荡，在弹丸通过瞬间，应力迅速增大，随后波动衰减。但是当速度较大时，应力波反而有增大趋势，这是由于应力波振荡频率接近材料固有频率时引起的共振所造成的。该应力将导致复合材料层和金属内衬层界面的分层破坏。

复合材料最内层的周向应力如图11所示。周向应力过大是造成复合材料层纤维断裂和基体撕裂的主要因素。其与切应力有相同的变化趋势，但是切应力有可能是负值，而周向应力只有正值。对比两条曲线，情况2中的波峰出现时间更早，也更为陡峭；波长更短，说明频率更高；衰减过程有轻微共振。

两种速度情况下，复合材料最外层的轴向应力随时间的演化曲线如图12所示。

轴向应力的变化最能反应应力波的传播情况。从图12中可看出，其具有以上所有应力变化的特点，波长和振幅都相对均匀，情况2中的共振效应也更为明显。在材料破坏之前，两种速度情况下波峰的最大值变化不大，约为100 MPa。

4 结束语

应力波引起的动态响应具有潜在的破坏性，并缩短结构的疲劳寿命。笔者关于复合圆筒的动载分析揭示了当压力前缘沿圆筒轴向移动时圆筒中应力应变幅值的发展规律，以及伴随应力波传播而生的共振效应。与应力波有关的损伤扩展对于质量较小的复合材料圆筒尤为致命，因为多重材料层合结构界面处的剪切和拉伸强度较低，高温下材料属性下降，且加载速率对复合材料属性具有更大影响。笔者所做的动态分析极大地克服了以往对于复合身管和管道系统设计、尤其减重设计时所做静态分析中的缺点。该动态响应分析和破坏原理为发展一个安全实用的设计方法具有重要理论参考和指导意义。