等离子体点火密闭爆发器中压力信号的小波分析

宗思佳，杨春霞，栗保明

(南京理工大学 瞬态物理国家重点实验室，江苏 南京 210094)

密闭爆发器实验是研究电热化学炮等离子体点火和发射药燃烧的重要手段，实验中火药气体对外没有做功，发射药处于定容燃烧状态，通过测量密闭爆发器实验的燃气压力，研究发射药在等离子体作用下的燃烧特性[1-2]。压力测量中由于量化电平、多处强电磁噪声和燃烧等现象耦合造成数据抖动，导致实验测得的压力信号存在“毛刺”现象[3-4]。因此，降低密闭爆发器实验中压力信号的噪声干扰，对等离子体与发射药间相互作用的机理研究具有重要意义。

常用的滤波降噪方法有傅里叶法、短时傅里叶法和小波分析法等。由于小波分析具有时频局部化和多分辨率分析的特点，近年来成为非稳态信号处理的首选工具，在图像处理[5]、医疗成像[6]、通讯语音[7]、地质[8]及军工数据[9]等方面具有广泛的应用前景。在电热化学炮方面，林庆华等[10]采用消失矩为8的Daubechies小波基函数，将等离子体点火密闭爆发器实验的压力信号进行5层小波分解，得到信号的时频特征。而在小波阈值去噪的实际应用中，小波基函数、分解级数及阈值方法等参数均对去噪效果产生影响，为达到最佳去噪效果，需通过建立合理的评价体系来选择小波参数。笔者建立多指标融合的评价体系，分析不同小波参数下密闭爆发器实验压力信号的去噪效果，确定去噪效果最佳的参数，根据势平衡理论对去噪后的压力曲线进一步计算，通过不同输入电能条件下等效势平衡点处ψe值的变化分析密闭爆发器实验发射药的燃烧特性。

1 实验系统介绍

图1为等离子体点火密闭爆发器实验系统结构示意图，该系统由脉冲功率源、等离子体发生器、密闭爆发器实验装置和测试系统组成[11]。

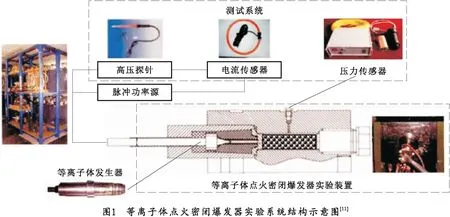
测试系统中，燃气压力采用Kistler 6215压力传感器(精度为1%)测量，等离子体发生器两端的电压和电流分别采用Tektronix高压探针和Rogowski线圈测量，为避免电缆传输通路的电磁干扰和地回路的影响，采用光电隔离传输技术(精度为0.5%)来提供高宽带和稳定的直流信号传输通路，通过JV5200瞬态记录仪(采样速率为5 MS/s)对压力信号进行采集记录[12]。

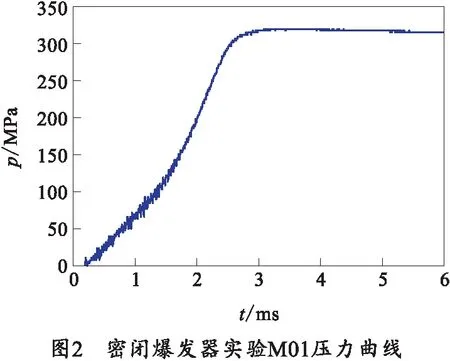
实验采用单个电源模块放电，模块电感为40 μH，发射药为4/7单基药，装药量为36.1 g，燃烧室容积为145 cm3，测得的压力曲线如图2所示。从图中可以看出，曲线中含有过多毛刺，为了降低研究误差，应先对数据进行除噪处理。

2 评价体系建立

小波去噪常用的评价指标主要包括均方根误差RMSE、信噪比SNR、互相关系数R和平滑度r等[13-14]。均方根误差反映了去噪信号和原始信号的离散程度，体现了去噪的准确性；平滑度反映了去噪信号的局部特征，体现了曲线的光滑性，且二者都呈负相关性，值越小去噪效果越好[15]，因此笔者选择均方根误差RMSE和平滑度r建立评价体系。为了将两个指标进行融合，需进行归一化处理，使数值在[0,1]区间内，归一化方法为

(1)

(2)

式中：SRMSE和Sr为归一化后各待比较参数的均方根误差与平滑度；RMSE和r分别为各待比较参数的均方根误差与平滑度；下标max和min分别为取最大、最小值。

确定评价指标后对各指标赋权，常用的赋权方法有熵权法、变异系数法和离差法等[16]。变异系数法是通过各指标所包含的信息计算权重，其基本思想是变异系数越大的指标为越难以实现的指标，更能反映被评价单位之间的差距，则权重越大。选择变异系数法为SRMSE和Sr赋权，变异系数为标准差与均值的比值：

(3)

(4)

(5)

(6)

Z=WSRMSESRMSE+WSrSr，

(7)

式中：σSRMSE、μSRMSE分别为一组待比较参数的均方根误差值归一化后的标准差和均值；σSr、μSr分别为一组待比较参数的平滑度归一化后的标准差和均值；PSRMSE和PSr分别为归一化后的均方根误差和平滑度的变异系数；WSRMSE和WSr为PSRMSE和PSr变异系数的权值；Z为SRMSE和Sr融合后的复合评价指标。

3 势平衡理论分析

发射药在密闭爆发器中的燃烧为定容变质量过程，而在实际膛内的燃烧则是变容变质量过程，由于燃烧条件和环境的不同，发射药的实际燃烧规律也不同。在势平衡理论中，对势平衡点处的ψe值而言，它是标志燃烧面发生突变的点，仅与药形和尺寸的散布情况有关，因此用密闭爆发器实验的p-t曲线拐点处的ψe值代表实际膛内发射药势平衡点处的标志量，可代替火炮压力曲线的测量[17]。将密闭爆发器p-t曲线的拐点作为等效势平衡点，通过式(8)求ψe[11]：

(1-c1)fωψ+(k-1)cpEp,

(8)

式中：p为燃气压力；燃烧室容积V0=145 cm3；装药量ω=36.1 g；发射药密度ρ=1.6 g/cm3；发射药火药力f=960 J/g；余容α=1 cm3/g；c1=0.135 2，为固体发射药燃烧过程中的热散失系数[12]；ψ为发射药相对已燃百分数；k为比热比；Ep为输入发生器的电能；cp为等离子体点火过程中电能利用系数，即

(9)

式中，pm为最大燃气压力。电能利用系数受装填条件、峰值压力和输入发生器电能影响，电能利用系数越大表明输入发生器的电能利用率越高。

4 小波阈值去噪的参数选择

4.1 小波基函数选择

小波分析用于去噪时首先需要选定一种小波基函数对信号进行分解与重构。离散小波变换中常用的小波基函数有Daubechies(dbN)小波、Symlets(symN)小波族、Biorthogonal(biorNr.Nd)小波族和Coiflet(coifN)小波族，其中N为消失矩，Nr和Nd分别是与重构和分解滤波器长度有关的参数。

为分析某一参数对去噪效果的影响，采取控制变量法，将分解级数设为5，阈值采用Birge-Massart策略确定。求得阈值后，有两种在信号上作用阈值的方法：一种是令绝对值小于阈值的信号点值为0，为硬阈值；另一种软阈值方法是在硬阈值的基础上将边界出现不连续点收缩到0[18]。硬阈值函数的缺点是会在某些点产生间断，软阈值可以有效地避免间断，使重建信号比较光滑，因此选择软阈值处理方法。分别采用db小波、sym小波族、bior小波族和coif小波族4个小波基函数对M01实验的压力曲线进行降噪，对去噪后的曲线由式(1)～(7)计算求出复合评价指标Z，根据Z值选择去噪效果最佳的小波基函数与消失矩，结果如表1～4所示。

表1 Daubechies小波基函数求得的Z

表2 Symlets小波族函数求得的Z

表3 Biorthogona小波族函数求得的Z

表4 Coiflet小波族函数求得的Z

由于平滑度与均方根误差均呈负相关性，则复合后的评价指标Z值越小说明去噪效果越好[15]，对比表1～4中各小波基函数在不同消失矩下的Z值，分别选择db8、sym8、bior3.7、coif5这4个小波基函数进一步确定最优阈值处理方法和分解级数。

4.2 阈值处理方法选择

在确定小波基函数后，进一步分析阈值处理方法对小波去噪效果的影响，小波分析中有两种阈值确定方法：一是从原始信号确定各级阈值；二是基于样本估计的阈值确定方法[18]。Birge-Massart策略是从原始信号中确定各级阈值，常用的基于样本估计的阈值确定方法还有rigrsure阈值、sqtwolog阈值、heursure阈值和minimaxi阈值。在确定小波基函数后，保持分解级数为5不变，分别计算5种阈值方法的Z值，结果如表5所示。

表5 不同阈值方法下求得的Z

从表5中可以看出在rigrsure阈值方法下的Z值最大，分析认为这是由于等离子体点火密闭爆发器实验的压力信号中耦合的噪声为高频信号，而rigrsure阈值方法在高信号噪声比的情况下抑制噪声的效果不明显。Birge-Massart策略下求得Z值与其他3种方法相比最小，分析认为这是由于实际等离子体点火发射药燃烧的过程较为复杂，导致信号噪声源较多，而采用基于样本估计的阈值确定方法具有局限性，因此选择Birge-Massart策略。

4.3 分解级数选择

确定小波基函数、阈值处理方法后，进一步选择分解级数，分别进行3～10层级数分解，分析比较不同分解级数下压力信号的去噪效果，结果如表6所示。

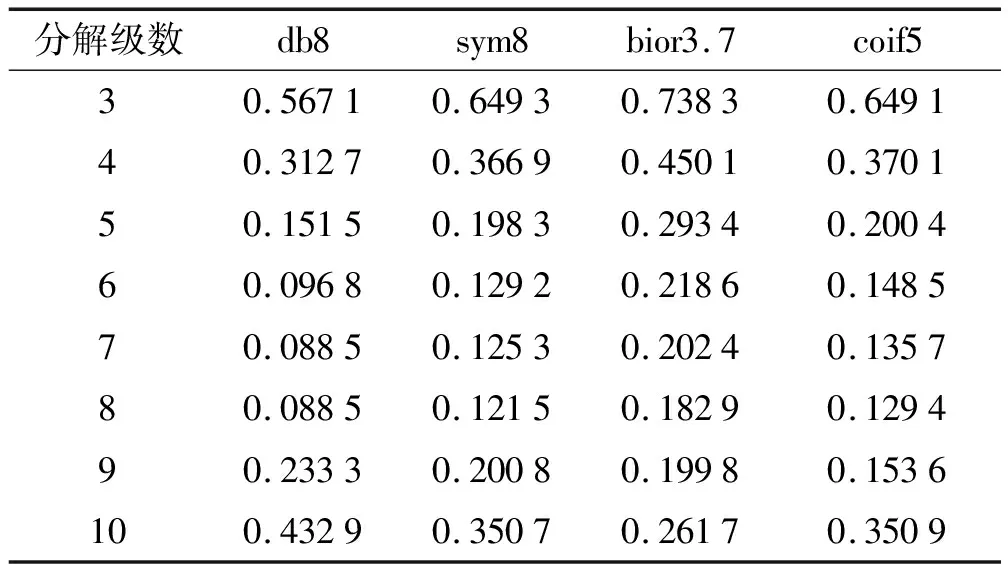
表6 不同分解级数下求得的Z

从表6中可以看出，随着分解级数的增加，Z值呈先减小后增大的趋势并在分解层数为8时达到最小值。随着分解层数的增加，近似函数中所含高频部分越少，将近似系数与细节系数经过阈值方法重构后的信号光滑度越高，对比4个小波基函数的Z值，最终确定小波基函数为db8，分解层数为8，Birge-Massart策略软阈值处理为此次实验压力信号去噪的参数和方法，此时均方根误差RMSE为2.244 5，平滑度r为0.123 3。

4.4 结果分析

将去噪处理后的压力曲线与实验测得的曲线进行比较，如图3所示，从图中可以看出经小波去噪后的曲线具有良好的相似性和光滑度。对去噪后的压力曲线进一步计算可得到压力梯度dp/dt随时间的变化关系，如图4所示。

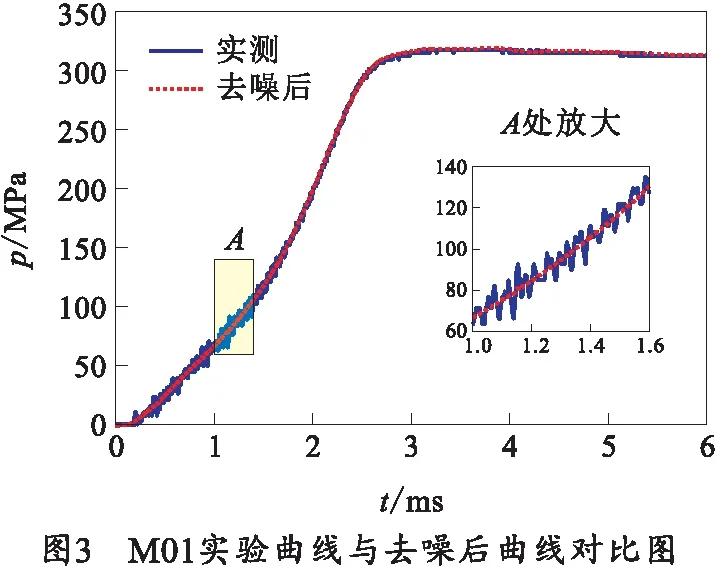
从图4中可以看出，等离子体点火密闭爆发器实验的压力梯度在脉冲放电初期迅速达到峰值70 GPa/s，随着发射药开始燃烧，压力梯度达到第2个峰值90 GPa/s，此后至0.9 ms内压力梯度呈下降趋势，脉冲电源在0.9 ms时刻放电结束，之后随着发射药继续燃烧，压力梯度保持稳定增长，在2.07 ms到达最大值约为206 GPa/s。在3.2 ms时刻dp/dt=0，表示此时发射药燃烧结束，燃气压力达到峰值约为319 MPa，随后燃气压力应保持不变，而在实际燃烧过程由于壁面热散失等原因使燃气压力有所下降，压力梯度产生波动。

对燃气压力梯度进一步计算，如图5所示。

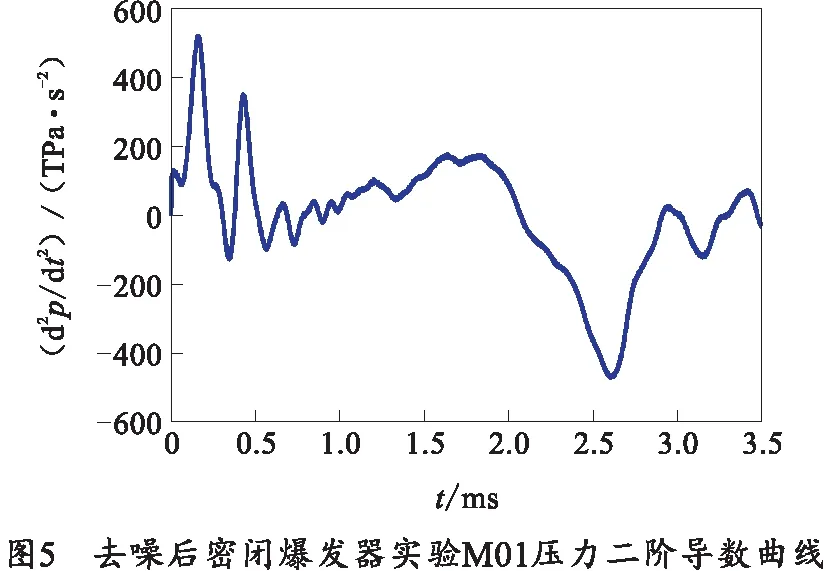
当2.07 ms燃气压力梯度达到峰值时，此时d2p/dt2=0，该点即为密闭爆发器p-t曲线的拐点，燃气压力为214 MPa。输入等离子体发生器的电能Ep=48.2 kJ，利用式(8)求出ψe=0.655 4，该点标志着燃烧面发生突变，为发射药分裂点。

采用上述评价体系选择最优小波阈值参数对不同输入电能Ep下等离子体点火密闭爆发器实验的压力信号进行去噪处理，对去噪后的压力曲线进一步计算得到拐点处燃气压力pe与时间te，代入式(8)可得势平衡点处发射药相对已燃百分数ψe值，根据实验曲线的最大压力pm值计算电能利用系数cp，将常规点火与等离子体点火密闭爆发器实验的计算结果进行对比，如表7所示。

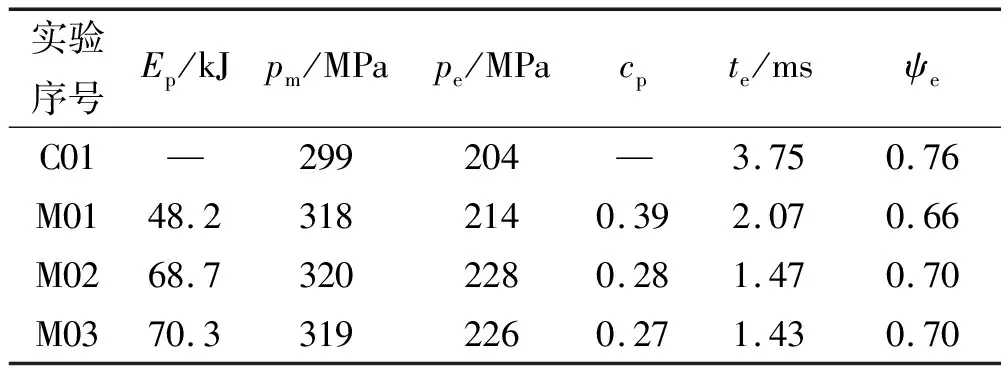
表7 不同输入电能条件下等效势平衡点ψe值

从表7中可以看出，与常规点火C01相比，等离子体作用下等效势平衡点处压力升高，达到等效势平衡点的时间缩短，对应ψe值减小。这是由于一方面输入发生器的电能放电产生等离子体点燃并增强发射药燃烧，使发射药燃速增加，燃烧时间缩短，燃气压力提高，同时一部分电能作为发射药能量的补充使相同质量下发射药的能量提高，拐点处ψe值减小。对比等离子体点火密闭爆发器实验M01～M03，当燃烧室容积与装药量一定时，电能利用系数的计算主要受最大燃气压力和输入电能的影响，由于电能对燃气压力的提高有限，当输入发生器电能增加时，峰值压力变化较小，电能利用系数降低，表明当燃烧室容积V0一定时，输入电能Ep与发射药装药量ω具有一定的匹配关系。

5 结束语

笔者对等离子体点火下密闭爆发器实验的压力信号进行去噪处理，采用小波阈值法，选择均方根误差和平滑度建立多指标融合的评价体系，分析不同小波基函数、阈值方法、分解级数条件下的密闭爆发器实验压力信号去噪效果，最终确定小波基函数为db8，Birge-Massart策略下，分解级数为8层时，经软阈值处理后的信号去噪效果最佳。根据势平衡理论对去噪后的压力曲线进一步计算，分析不同输入电能条件下密闭爆发器实验压力曲线ψe值的变化。结果表明，等离子体作用下等效势平衡点处压力升高，达到等效势平衡点的时间缩短，对应ψe值减小。