低信号下利用回归模型提高雷达测速精度方法

田珂

(中国人民解放军63861部队，吉林 白城 137001)

靶场的所有试验中，利用初速测量雷达测试弹丸的炮口初速是最常开展的试验科目，因为炮口初速关系到火炮武器系统能否精确打击敌方目标[1]。因此利用初速测量雷达能否准确测试弹丸的炮口初速，关系到火炮武器系统的战斗性能能否满足战场要求，更关系到战场上能否战胜敌人。但是在某型大口径弹丸试验中，由于弹丸受到自身或者外界因素的影响，使得雷达捕获的信号不完整，从而无法准确计算出真正的初速数据，严重影响着试验任务的正常开展，而解决这一问题的方法和文章还很少。由于大口径弹丸试验时某型初速雷达测试弹丸的炮口初速是可以近似根据雷达测试弹丸的径向速度递推出来的，所以为了解决这一突出问题，选择在等时间间隔的基础上加载雷达测试的弹丸径向速度，针对有的时刻雷达没有获取到弹丸径向速度的情况，利用回归模型预测出缺失的径向速度，等补齐所有径向速度后再利用回归模型拟合递推出弹丸的炮口初速。为了证明该方法的正确性，把利用该方法计算出的初速数据与信号完整的雷达测试的初速数据进行对比并计算误差，发现采用该方法计算出的初速数据很接近信号完整的雷达测试的初速数据，两者的误差明显小于两台雷达原始初速数据的误差，说明该方法能够提高雷达在低信号下的测速精度。

1 回归模型建模步骤

回归一词最早是由英国著名统计学家高尔顿及其学生皮尔逊提出来的。回归分析是一种统计学上分析数据的方法，目的在于了解两个或多个变量间是否相关、相关方向与强度，并建立数学模型以便于通过观察特定变量来预测或控制研究者感兴趣的变量，它是一种典型的有监督的学习方法[2]。初速雷达测试弹丸的炮口初速通常采用线性回归模型和多项式回归模型[3]进行拟合递推，而针对大口径弹丸的试验，通常采用一元线性回归模型拟合递推初速数据，因为初速数据本质上是速度与时间的一元关系。

线性回归模型是用一个或多个自变量来解释因变量的统计分析模型。假设因变量用Y表示，n个自变量用X1,X2,…,Xn表示，用来解释因变量Y，则多元线性回归模型可表示为

Y=b0+a1X1+a2X2+…+anXn，

(1)

式中：b0为常数项；未知参数a1，a2，…，an称为回归系数。

假设自变量X和因变量Y分别表示为[4]

那么一元线性回归方程的数学表达式可表示为

Y=b0+aX，

(2)

式中：b0为常数项矩阵；a为回归模型的回归系数矩阵。假设有训练集D={(x1,y1),(x2,y2),…,(xn,yn)}，建立回归模型的目标是找到一条直线，使所有样本数据尽可能落在它的附近，这一目标可以通过最小化残差平方和(Residual Sum of Squares,RSS)来实现，当残差平方和达到最小值时这条直线就是最好的回归拟合线，进而寻找出最优的参数[2,5]，即目标转化为

(3)

将残差平方和fRSS(a,b)分别对a和b进行求导并令导数等于0，从而得到最优解：

(4)

一元线性回归模型主要解决的问题分为3个方面：

1)利用样本数据估计模型的回归系数；

2)检验线性回归方程和回归系数的显著性；

3)根据新的自变量X预测因变量Y。

检验一元线性回归模型及其系数显著性的目的是检验模型的拟合效果，通常采用F检验法，其原理是：如果F检验结果统计量t对应的概率p值小于0.05，说明回归模型是显著的，即回归模型方程通过了显著性检验。然后把可解释的平方和除以总平方和得到R2，作为线性回归拟合优度指标，如果R2大于0.8，则说明模型拟合效果较好。其中，可解释的平方和指的是因为回归线带来的变异，总平方和指的是数据本身的变异，显然可解释的变异占总平方和比例越大，即R2越大，说明回归模型拟合效果越好[5]。回归系数的显著性检验，是根据截距估计值和变量的回归系数估计值t统计量对应的概率p值与临界统计值0.001进行比较，如果p<0.001，证明截距估计值和回归系数估计值都非常显著。

2 线性回归模型提高雷达测速精度

初速雷达测试大口径弹丸的炮口初速通常选择0.1～0.5 s内的径向速度值进行拟合递推。在雷达获取到的弹丸信号很完整时，雷达每隔1 ms就会获取到一个径向速度数据，这时雷达自带算法能够很准确地计算出弹丸的初速数据。但是，当雷达获取到的弹丸信号不完整时，有的时间点就没有径向速度数据，此时采用雷达自带算法计算出的初速数据就会出现偏差。如图1、2所示的是两台初速雷达同时参与试验，测的是同一发弹丸，对称布置在火炮两侧，布站参数基本一致，结果一台雷达获取的弹丸信号基本完整，而另一台雷达获取的弹丸信号就缺失了一部分，导致两台雷达计算出的初速数据偏差很大。为了解决这一问题，在雷达获取的弹丸信号不完整的情况下，按照等时间间隔选择数据点的原则，选择从0.1 s开始每隔5 ms选取一个径向速度数据，一直取到0.5 s为止，总共获取到81个径向速度数据。但是由于雷达获得的信号不完整，有的时间点是没有径向速度数据的，同时初速雷达测试的弹丸径向速度与时间是一元线性关系，适合建立一元线性回归模型[6]。因此选择把缺失径向速度数据时刻之前的所有径向速度数据作为样本数据，建立径向速度与时间的一元线性回归模型，时间是自变量，径向速度是因变量，然后再利用训练好的回归模型预测出缺失的径向速度数据，然后再把下一个缺失值之前的所有径向速度数据作为样本数据建立一元线性回归模型，预测出缺失的径向速度数据。按照此方法依次预测出0.1～0.5 s所有缺失的径向速度数据，最后再对该81个径向速度数据建立一元线性回归模型，再利用建立好的回归模型拟合递推出该发弹丸的初速数据，并利用F检验法检验模型及回归系数的显著性。

图3是某型初速雷达测试的弹丸在信号不完整的情况下从0.1～0.5 s之间每隔5 ms选取的所有径向速度值，其中在时刻0.130、0.150、0.170、0.205、0.225、0.245、0.280、0.300、0.320、0.355、0.375、0.395、0.430、0.450和0.470 s雷达没有获取到弹丸径向速度数据。在图3的基础上利用回归模型预测并补全缺失的径向速度，然后把所有径向速度数据与时间对应起来，建立速度与时间v-t的一元线性回归模型[7]，最后利用所建模型拟合递推就得到了图4，拟合递推结果如表1所示，表中截距估计值就是计算出的信号不完整弹丸的炮口初速。

表1 某大口径弹丸低信号下回归拟合结果

3 实验验证

实验选择利用RStudio软件环境中的回归模型工具包进行模型的构建、训练及仿真，并选取同一试验中雷达A和雷达B共同测试的9发初速数据进行分析验证。其中雷达A测试的弹丸信号很完整，所选出的81个时刻点的径向速度数据都是完整的，采用回归模型直接拟合递推即可。雷达B测试的弹丸信号不完整，所选出的径向速度数据存在缺失，预测出缺失值后再拟合递推，预测的每一发径向速度数据经过F检验法检验，发现所建预测模型都是显著的，模型拟合结果都为好，回归系数和截距估计值都是显著的。针对雷达A和雷达B的所有拟合回归初速值，利用F检验法检验得出，所建立的速度与时间的一元线性回归模型均显著，模型拟合效果均为好，所得到的回归系数及截距估计值都是显著的[8]。表2列出了雷达A和雷达B测试的9发初速数据的实测值以及采用所述方法得到的拟合回归值。

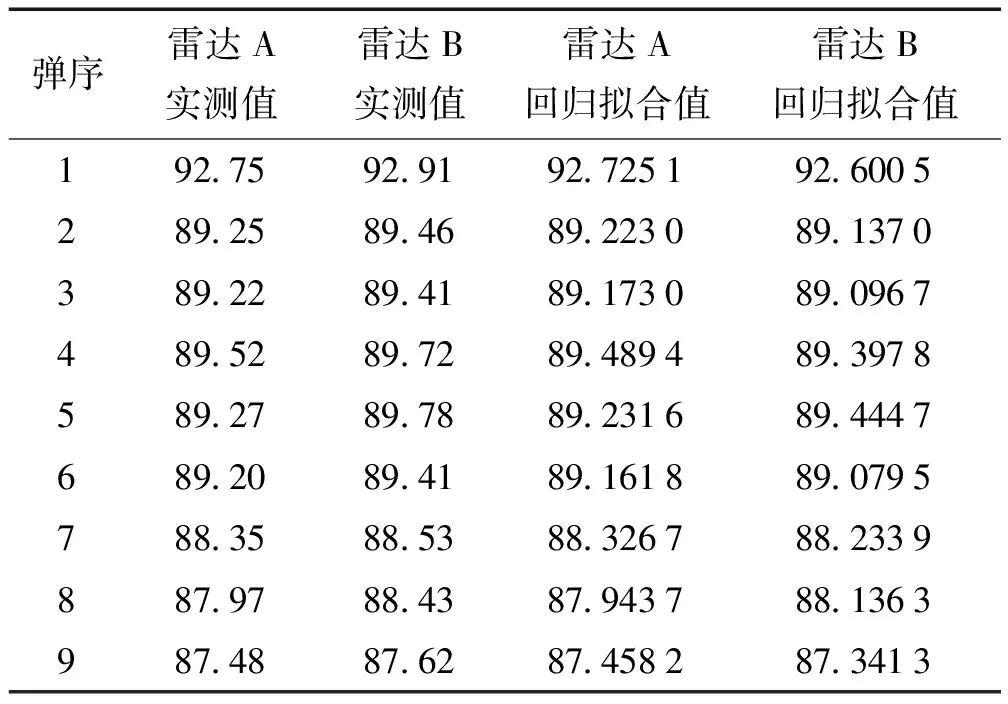
表2 某型试验两台雷达实测值及回归拟合值 m·s-1

图5是雷达A和雷达B测试的9发弹丸初速实测值及其拟合回归值的时间序列图。

因为雷达A测试的弹丸在所有时刻的径向速度数据都不存在缺失，即弹丸信号是完整的，雷达B测试的弹丸在有的时刻径向速度数据存在缺失，即信号不完整，而且经过计算得到雷达A的9发实测值与雷达B的9发实测值的平均相对误差为0.281%，超出了靶场试验中两台初速雷达测试弹丸初速2‰的误差标准，所以初步判断雷达A测试的弹丸初速数据是准确的，雷达B测试的弹丸初速数据是不准确的。从图5可以直观看出，雷达A测试的9发弹丸的拟合回归值非常逼近雷达A的实测值，而且雷达B测试的9发弹丸的拟合回归值也非常逼近雷达A的实测值，即采用同样的方法计算出的两台雷达的拟合回归值都非常逼近雷达A的实测值，所以确定出雷达A测试的9发弹丸初速数据才是弹丸炮口初速的真实值。同时经过计算得到雷达A的9发拟合回归值与雷达A的9发实测值的平均相对误差为0.035%，满足靶场试验中单台初速雷达测试弹丸初速1‰的误差要求[1]，这就充分证明了在等时间间隔加载径向速度数据的基础上，利用回归模型拟合递推初速数据的方法是正确可行的。采用该方法计算出的雷达B的9发弹丸拟合回归值与雷达B的9发实测值的平均相对误差为0.348%，超出了靶场试验中单台雷达测试弹丸初速1‰的误差要求[1]，而与雷达A的9发实测值的平均相对误差为0.152%，满足靶场试验中两台初速雷达测试弹丸初速2‰的误差标准，总体平均相对误差更小[9]，回归模型能够很好地挖掘出弹丸径向速度中的变化规律并提高拟合精度[10]，说明所采用的方法提高了雷达B在信号不完整情况下测试弹丸初速的精度。

4 结束语

某型试验中利用两台初速雷达测试弹丸炮口初速经常会遇到弹丸信号不完整、计算出的初速数据偏差过大的情况。为了解决这一问题，在等时间间隔基础上加载径向速度数据，利用回归模型预测出缺失的径向速度数据，再通过建立速度与时间的一元线性回归模型拟合递推出初速数据。实验证明该方法是正确可行的，能提高雷达在弹丸信号不完整情况下的测速精度。