基于改进Otsu-Sobel的分体式炮弹缝宽视觉测量方法研究

孟向臻，姜春英，丁美杰，徐永利，徐志刚

(1.沈阳航空航天大学，辽宁 沈阳 110136；2.中国科学院 沈阳自动化研究所，辽宁 沈阳 110016)

分体式大口径后膛炮的弹体主要采用螺纹连接，螺纹连接的扣数对于炮弹的发射质量至关重要[1]。分体式炮弹缝宽大小是检测螺纹连接情况的重要指标之一。传统的缝宽检测方法是进行人工手动测量。因手动对带药的弹丸进行检测，具有一定的危险性；且由于缝宽细小，使得操作者不易观察，导致测量结果一致性差、效率低。为了提高缝隙测量的精度与效率，保障操作人员的生命安全，非常有必要利用机器视觉的智能检测方法取代传统的人工操作环节，从而实现自动化、智能化的生产流程。笔者基于承担的相关项目，开展了分体式炮弹缝宽测量的应用研究。

关于弹药测量的研究，国内卢艳萍团队提出了一种基于工业CT成像的弹药缝隙测量方法[2]。胡备等基于激光位移传感器提出了一种水平台校准测量的方法，实现了对火炮身管内径测量的优化计算[3]。在机器视觉领域，缝宽测量即为边缘检测，刘天时等提出了一种自适应阈值的改进Prewitt算子[4]，提高了岩石边缘的检测率，但该方法对噪声异常敏感，在边缘线较粗的情况下会出现伪边缘。李军成构造了一种 0～1阶的分数阶Sobel算子[5]，分数阶微分能够检测出详细的边缘特征，对噪声有一定的抑制作用，但会出现边缘断裂的情况。雒涛提出一种改进的自适应阈值Canny检测算法[6]，高低双阈值的选取解决了人为因素导致的断边和伪边缘检测。梁肇峻等提出了一种基于Otsu的自适应Canny算法[7]，有效提高了Canny算法的定位精度与鲁棒性。

针对分体式炮弹缝宽高精度稳定测量这一特定研究问题，国内并未见相关文献报道。为了保证测量的相对误差小于0.02 mm，笔者提出了一种基于改进Otsu-Sobel的分体式炮弹缝宽视觉测量方法。

1 改进的Ostu-Sobel边缘检测算法

炮弹表面如图1所示。图1(a)中间深色区域为缝宽间隙。因为炮弹在螺纹拧紧后留下的缝隙宽度不同，所以在拧紧后需要对缝隙宽度进行精确测量。为提高缝隙图像的对比度以及抵消表面涂层颜色对缝隙测量结果的影响，采用两个LED条形光源照射圆柱体表面，如图1(b)所示。

因为缝隙边缘存在毛刺等缺陷，对打光后图像进行滤波降噪处理，通过Otsu阈值分割算法确定缝隙边缘的感兴趣区域，并在感兴趣区域内进行单调化处理。然后，利用Sobel算子确定阈值区间，以便对缝隙进行粗定位。最后，在所确定的梯度阈值区间内利用离散度获得精确的缝隙边缘。改进的Otsu-Sobel边缘检测算法流程图如图2所示。

1.1 图像滤波

为了弱化外界因素对缝隙测量的干扰，选用高斯函数对图像进行滤波处理。图3为0.16 mm缝隙图像灰度图，图像像素尺寸为64×64，缝宽长度为0.32 mm。图4为图像像素值的三维表示，其中高度信息代表像素值大小，从图4可看出滤波后的图片相比滤波前趋于平滑，有利于后续的图像处理。

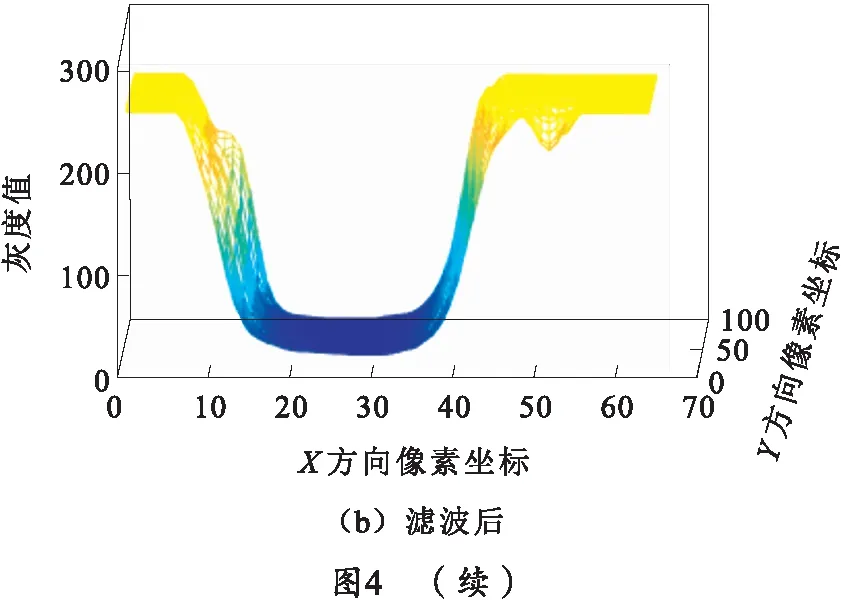
1.2 基于Otsu的自适应阈值分割方法

阈值分割通过设置一个阈值K，将图像分为两部分：

(1)

式中：f(x，y)表示像素坐标系下(x，y)处阈值分割后的像素值；K为选定的阈值。

基于最大类间方差的Otsu法因分割效果良好被广泛应用于图像的阈值分割[8-9]，故选用Otsu阈值分割的方法自适应选取阈值K：

K=Po(μ-μ′o)2+Pb(μ-μ′b)2,

(2)

式中：μ为图像的灰度均值；μ′o和μ′b分别为目标O和背景B的均值；Po、Pb分别表示前景与背景占全图的比例；当K取最大值时即为最佳阈值。

图5为缝隙图像原图，缝隙Otsu阈值分割效果图如图6所示。

在Otsu阈值分割中，阈值K容易受到光照强度变化、缝隙周围倒角、涂层破损和毛刺等外界因素影响而发生变化。阈值K选取过大会造成过度分割，阈值K选取过小会达不到分割效果，影响缝隙测量的精度。为了解决这一问题，笔者将阈值分割确定的感兴趣区域扩展20%，再利用后续边缘检测方法确定缝隙边缘。

1.3 改进的Sobel边缘检测算法

1.3.1 单调化处理

在Otsu算法确定的感兴趣区域内，图像灰度值曲线凹凸不平。为了保证Sobel微分的统一性以及提高边缘检测的效率，采用如式(3)所示的单调化处理方法。具体为：在感兴趣区域内以最小灰度值位置为起点，向两边判断下一个位置的灰度值是否小于目前的值，如果判断条件成立，则使得下一个位置的灰度值等于当前位置的灰度值。

(3)

式中：N(xi,yi)是坐标为(xi,yi)处的图像灰度值；(xT,yi)是灰度曲线中灰度值最小处的坐标值。单调化前后灰度曲线如图7所示。

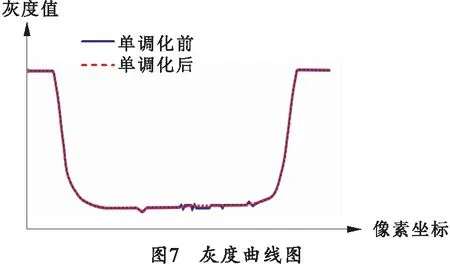
由图7可以看出，单调化之后的灰度曲线，没有了灰度值跳动的现象，具有了稳定的趋势。

1.3.2 Sobel边缘检测

当感兴趣区域内的灰度曲线完成单调化处理后，选取Otsu算法中小阈值峰顶处的灰度值作为第2个感兴趣区域的界限，在界限内将所有灰度值设置为界限内灰度值的最大值：

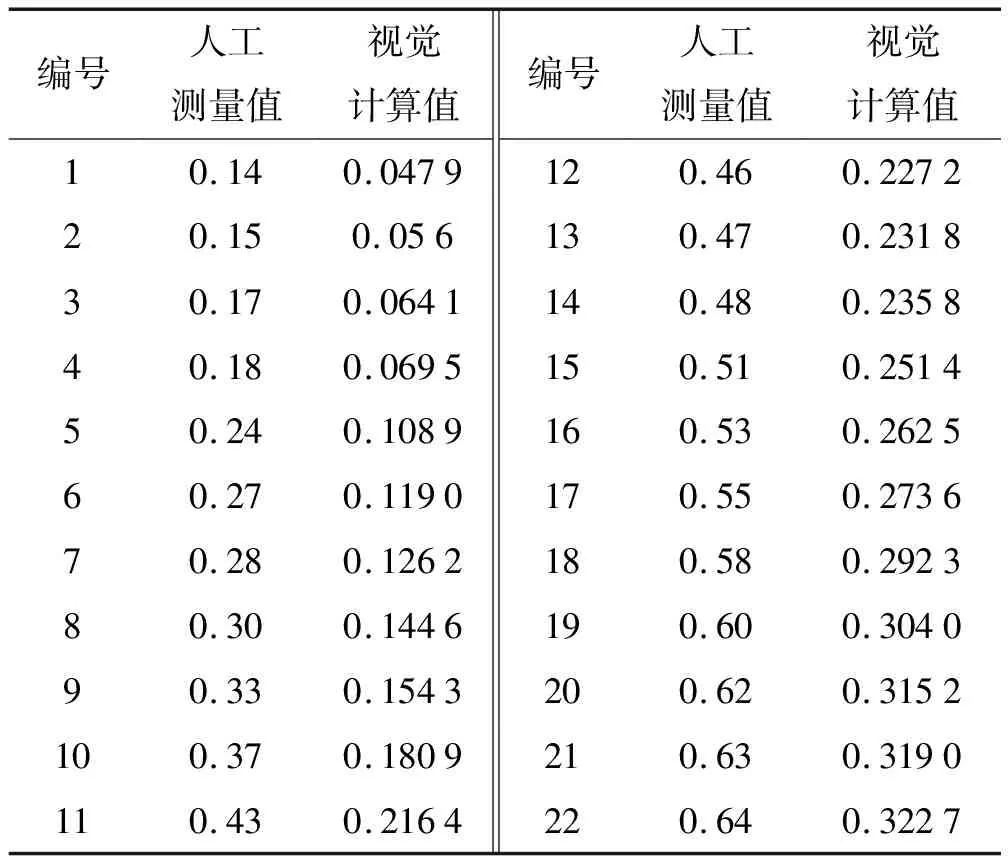
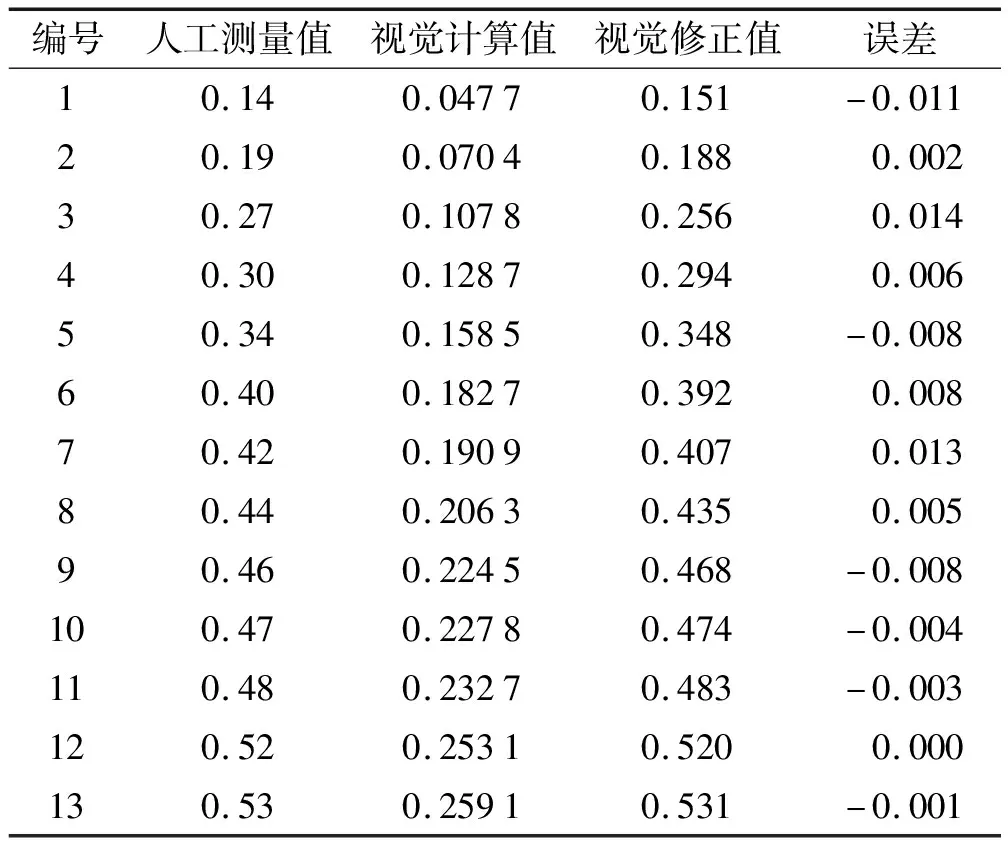
M(xi,yi)=max{M(xo,yi),M(xi,yi)},xn

(4)

式中：M(xi,yi)是坐标为xi处的图像灰度值；xo是第2个感兴趣区域内中灰度值最大处的坐标值；xn是第2个感兴趣区域的左边界坐标值；xm是第2个感兴趣区域的右边界坐标值。

将图像中的灰度信息单调化后，变化的灰度值将灰度值曲线分成若干区域，然后建立一个1*3的卷积模板，将卷积模板从灰度值最低点依次向两边移动并对灰度值曲线进行卷积依次计算梯度值：

(5)

通过多次实验分析，像素的梯度值如图8所示，梯度值分布从像素值最低点向两边逐渐变大。当梯度值大于5时，梯度值开始剧烈变化；当梯度值小于2时，梯度值会在0～1之间变化。因此选择[2,5]作为一阶微分算子计算缝宽边缘的粗定位区间。

1.3.3 局部精定位边缘

在改进的Sobel边缘检测算子确定的缝隙粗定位区间内，依次计算灰度值的均值μ和离散度δ，最后选取离散度最大的像素坐标作为缝隙的精定位边缘点。

(6)

式中，μ、δ、M×N分别表示像素值的均值、像素值的离散度、粗定位区域的大小。

2 基于最小二乘拟合的缝宽修正

由于硬件安装误差使得图像产生畸变，如图9所示，结果导致人工与视觉计算的缝隙宽度存在一定的误差。为了实现目标测量精度，笔者采用最小二乘拟合方法进行缝宽数据修正。

2.1 带通滤波消除断边影响

在计算出图像中每行像素的缝宽后，一阶微分算子会出现3种未找到边缘点的情况。此时，边缘点坐标为0，即断边现象：

(7)

当左边缘a与右边缘b，都未找到时，缝隙宽度为0；当左边缘a找到而右边缘b未找到时，缝隙宽度为负；当左边缘a未找到而右边缘b找到，缝隙宽度远大于0。当出现断边现象时，为了防止坏点对拟合精度带来影响，需在拟合前对测量数据进行带通滤波处理。由于测量的缝宽为0.1～0.7 mm，所以设置缝宽上限与下限分别为1.2 mm和0 mm。

2.2 最小二乘拟合修正

基于最小二乘的缝宽修正方法分为以下步骤：

1)先得到图像中经过带通滤波后的每行像素的缝宽，然后统计出相同像素缝宽的数量占所有像素缝隙宽度数量的权重，再将所有像素缝隙宽度乘以对应权重求和得到计算值：

(8)

式中：di为第i行的缝宽值的数量占全部缝宽值数量N的权重；ni为第i行缝隙值的数量；h为所有缝隙加权后计算的视觉缝隙值；βi为第i行的视觉缝隙值。

2)利用最小二乘法[10]拟合出视觉计算与人工测量缝宽之间的关系。拟合目标为给定缝宽的人工测量值集合{gi}，i=1,2,3,…，与视觉检测值的误差平方和E2最小：

(9)

式中：gi为样本的实际测量值；Hi为样本的平均视觉计算值；k为修正系数(包括缝隙倒角等影响)；α为缝隙与垂直线的夹角；E2为实际测量值与平均计算值之间误差的平方。最后，可得ω和b的最优解的闭式解：

(10)

3 实验

3.1 弹药螺纹连接处缝隙视觉测量系统

被测炮弹直径为120 mm，系统通过连续采集多张小样本图像，样本图像尺寸为0.76 mm×5 mm，降低了炮弹曲率对缝宽测量带来的非线性误差。

图像采集设备由高分辨率CCD黑白相机，型号为MER-1070-10GM，条形光源型号为JT-LSP150-W，镜头选用千万像素级别25 mm定焦镜头，型号为LM25JC10M组成。经过多次试验，测得最佳相机参数为:镜头工作距离为110～130 mm;光圈F为6～8；相机曝光时间为7 000 μs;图像采集帧率为14 Hz。图像的处理与分析在VC++(Microsoft Visual C++)环境下完成，如图10所示。

3.2 缝宽测量实验

为了验证本方法的有效性，分别针对0.12，0.22，0.35，0.57 mm缝宽图像进行分析，图像分辨率为1 520×1 000。缝隙原始灰度值分布与感兴趣区域内像素的梯度值分布如图11～14所示。

根据感兴趣区域内像素的梯度值分布图得出，缝隙图像经过Otsu阈值分割、单调化处理后，在区间[2,5]之间像素的梯度值变化较稳定。在确定区间[2,5]之间像素的梯度值后，通过计算区间内梯度的均值方差，将方差最大的像素坐标作为缝隙的精定位边缘。

专业检测人员利用塞尺得到22组不同缝宽值与视觉计算值的标定数据如表1所示，塞尺精度为0.01 mm，缝隙长度为0.76 mm。根据表1中的数据及式(8)～(10)，采用最小二乘拟合的方法，获得缝隙视觉计算测量值与人工测量值的拟合结果，如图15所示，得到视觉测量值修正公式：

表1 标定缝隙宽度表 mm

Y=1.817 5X+0.06,

(11)

式中，X、Y分别为标定前、后的缝宽值。

为了验证本文方法的有效性、鲁棒性。选取了多组不同宽度的缝隙进行测试，将视觉计算值代入式(11)得到最终的缝隙宽度值，与专业检测人员利用塞尺测量的缝宽值及单个工件检测时间(约为30 s)结果进行对比，计算误差ε：

ε=R-Y，

(12)

式中：R为专业检测人员的测量值；Y为视觉修正值。

本次实验采集的缝隙样本长度为0.76 mm，故本系统利用缝隙样本的平均缝宽值作为本样本的缝宽值。本次实验采集了13组缝隙数据，测量结果如表2所示。结果显示，专业检测人员利用塞尺测量值与视觉修正值的最大测量误差均小于0.02 mm，说明本文算法可以满足缝宽质量检测的需要。

表2 缝隙测量结果 mm

4 结束语

笔者利用机器视觉的方法，提出了一种基于Otsu-Sobel的分体式弹药螺纹缝宽视觉测量方法。通过Otsu阈值分割方法确定缝宽的感兴趣区域，利用改进Sobel算子确定缝宽边缘位置，再利用最小二乘法计算出缝隙的实际宽度。对0.1～0.7 mm的缝隙进行测量实验，结果表明，该方法的最大测量误差为0.02 mm；系统完成单次测量的时间为7.2 s，相比于人工检测时间(约为30 s)，系统在提高缝隙测量精度的同时效率提高了4倍，且测量精度可以满足其生产要求，为产品的质量与可靠性提供了重要保障。