基于变分模态分解的暂态扰动波形去噪算法

张明龙，张振宇,2，高 源，罗 翔，周振宇，朱 珂

基于变分模态分解的暂态扰动波形去噪算法

张明龙1，张振宇1,2，高 源1，罗 翔1，周振宇3，朱 珂3

(1.国网福建省电力有限公司电力科学研究院，福建 福州 350007；2.福建省高供电可靠性配电技术企业重点实验室，福建 福州 350007；3.山东大学电气工程学院，山东 济南 250061)

针对经验模态分解去噪时存在的模态混叠问题，提出一种变分模态分解与滑动均值滤波相结合的去噪算法。首先通过寻找变分模型最优解将含噪信号分解成若干个固有模态。然后利用相关系数准则确定最优分解层数K以及其对应的相关模态，并用滑动均值滤波器对非相关模态进行处理以得到其中的有用分量。最后基于相关模态和非相关模态中提取的有用分量构造去噪后的信号。仿真表明，与经验模态分解去噪和小波去噪相比，所提出的算法能够在更有效去除暂态扰动中噪声的同时，保留暂态扰动中的特征信息。

暂态扰动；变分模态分解；相关系数；滑动均值滤波；去噪

0 引言

随着负荷对供电质量的要求日益提高，暂态电能质量问题越发突出。然而在获取暂态扰动波形数据时，难免会引入各种各样的噪声信号[1]，影响后续扰动波形分析的准确性，因此对暂态扰动波形数据进行降噪处理具有实际意义。

近年来，国内外学者对波形数据的降噪开展了卓有成效的研究。小波变换由于其时频域特性在暂态扰动波形去噪方面得到了广泛应用，根据扰动信号和噪声不同的行为特征，基于小波变换去噪的方法可以分为小波变换模极大值去噪[2]，小波尺度相关性去噪[3-4]以及小波阈值去噪[5-13]。小波基、小波分解层数和阈值的选择没有固定的标准，并且不同的小波基去噪结果相差较大[14]。经验模态分解(EMD)从信号自身的特点出发，将信号自适应地分解为一系列固有模态函数(IMF)，通过对含有噪声的IMF分量的处理以达到去噪的目的[15-16]。EMD在保留了小波多分辨率优势的同时克服了小波变换中小波基选择的困难，但EMD理论依据不够充分，模态分解过程中可能存在的数据间断点会引发模态混叠现象，导致信号有用信息丢失[17]。

针对EMD存在的上述问题，本文提出一种变分模态分解(VMD)和滑动均值滤波相结合的去噪方法。VMD将信号的分解过程转化为对非约束性变分问题的最优求解，抑制了经验模态分解存在的模态混叠现象，在频域通过不断迭代求解，实现了信号的自适应分解[18]。基于信号性质，利用相关系数和均方误差确定分解层数。此外为进一步提高信噪比，结合滑动均值滤波，较好地实现了对暂态扰动信号的去噪处理和信号保留。

1 变分模态分解原理

变分模态分解主要包括变分问题的构造和求解两个过程[19]。

1.1 构造变分模型

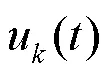
1) 利用Hilbert变换计算每个IMF的解析信号，从而得到每个IMF的单边频谱，相关解析信号为

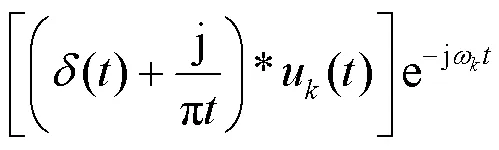
3) 通过对解调信号进行高斯平滑，计算出梯度的平方范数，估计出各固有模态函数u()的带宽，从而得到如下约束变分模型[20]：

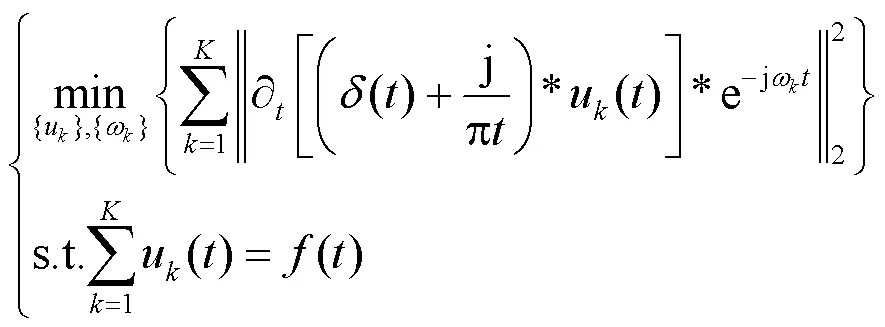
1.2 变分模型求解

1) 为了对上述约束变分模型进行求解，VMD算法引入了具有较强约束能力的拉格朗日乘子和二次惩罚项因子。对式(4)进行改造后获得的增广Lagrange函数表达式如下：

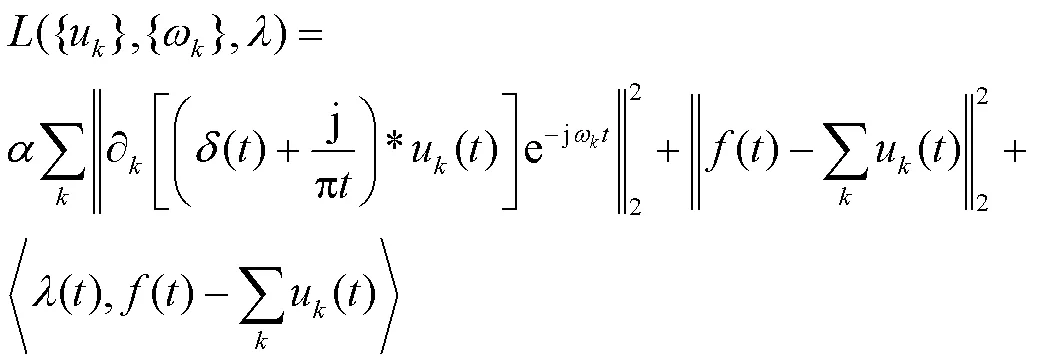
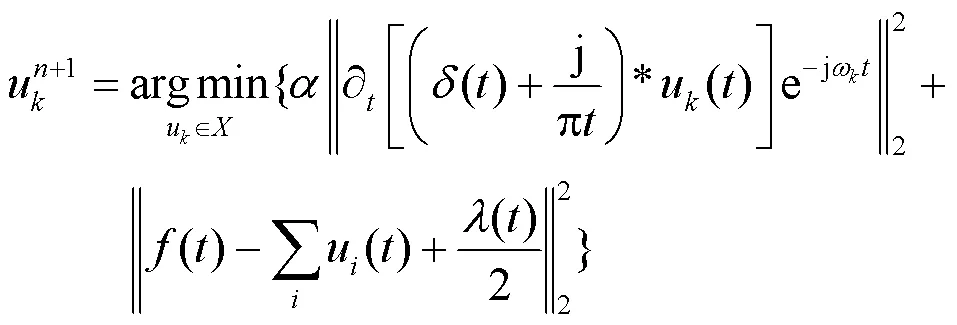
3) 在L2范数下，利用Parseval/Plancherel傅里叶等距变换将式(6)转换到频域并进行变量替换，然后在非负频率区间进行积分，最终可求得该二次优化问题的解为

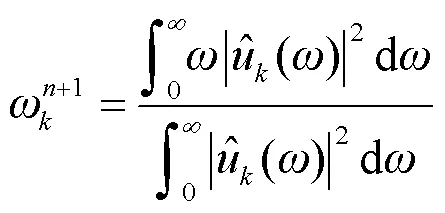
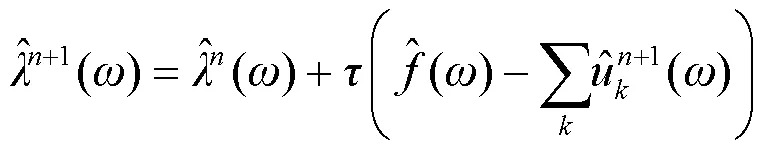
2 基于变分模态分解的去噪算法

2.1 相关模态的选取

在使用VMD算法对信号进行分解时，需要提前设置好信号的分解层数，对信号的频带进行正确的划分，值设置的正确与否直接关系到分解结果的精确性[21]。

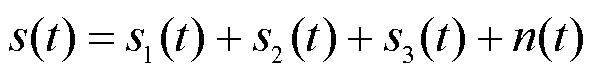
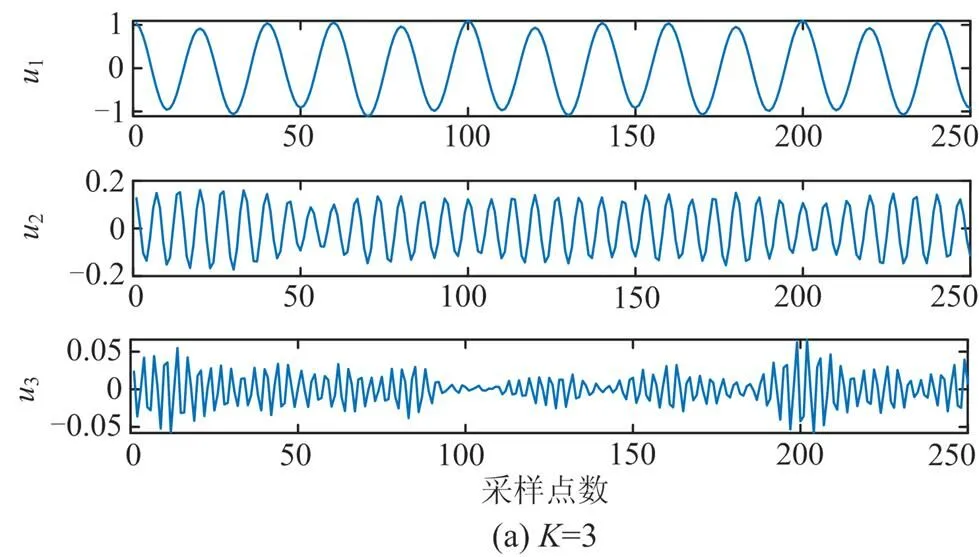
由图2可以看出：如果设置较小，使得输入信号中的多个有效成分被分解到同一个模态分量中，会造成有效分量的信息提取不完全；反之，如果设置过大，可能会造成输入信号中的某个成分被过分解，产生虚假模态。为了更好地选取分解层数，本文采用一种基于相关系数的值确定方法。

图1 含噪信号

1) 皮尔逊相关系数

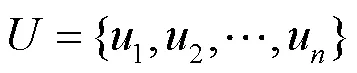
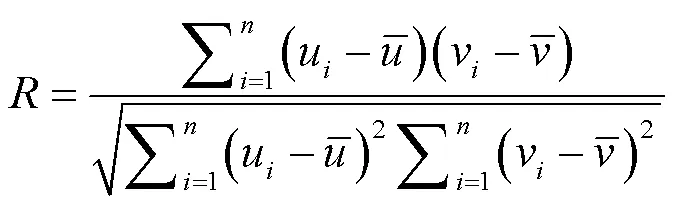
2) 基于相关系数的值选取方法

为选取合适的分解层数，本文使用均方误差MSE衡量重构信号与输入信号之间的差异程度。

钟鼎创投合伙人尹军平则给出了更为具体的辨别方案，以提升并购整合成功的概率。“第一是在选择潜在标的时，重点考察财务真实性，职业化水平、规范化难度。第二是先参股磨合一段时间，再考虑进行收购。第三是优先考虑优秀VC、PE投资过的项目。”

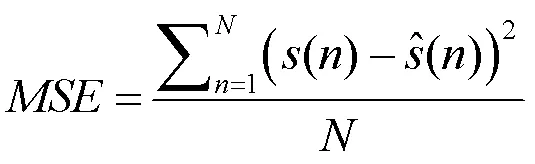
设定分解层数的取值范围，然后对于不同的值分别使用皮尔逊相关系数筛选出信号的相关模态，去除受噪声影响较大的模态分量，并进行信号的重构，最后分别计算重构信号与原信号的均方误差。当重构信号与输入信号的均方误差最小时，则认为原信号中的非相关模态绝大部分为噪声，所对应的分解层数即为合适的分解层数。

2.2 非相关模态的处理

上述算法在获得了最优值的同时筛选出了相关模态，为了进一步提高去噪信号的信噪比，对剩下的非相关模态使用滑动均值滤波[23]进行处理，提取其中的有用信息。

式中：W表示第个滤波窗口内信号点的集合；m表示滤波窗口的中心值；表示窗口半径。

2.3 基于VMD的暂态扰动波形去噪算法

基于上文分析，可以得到基于VMD的去噪算法的具体步骤为如图3所示。

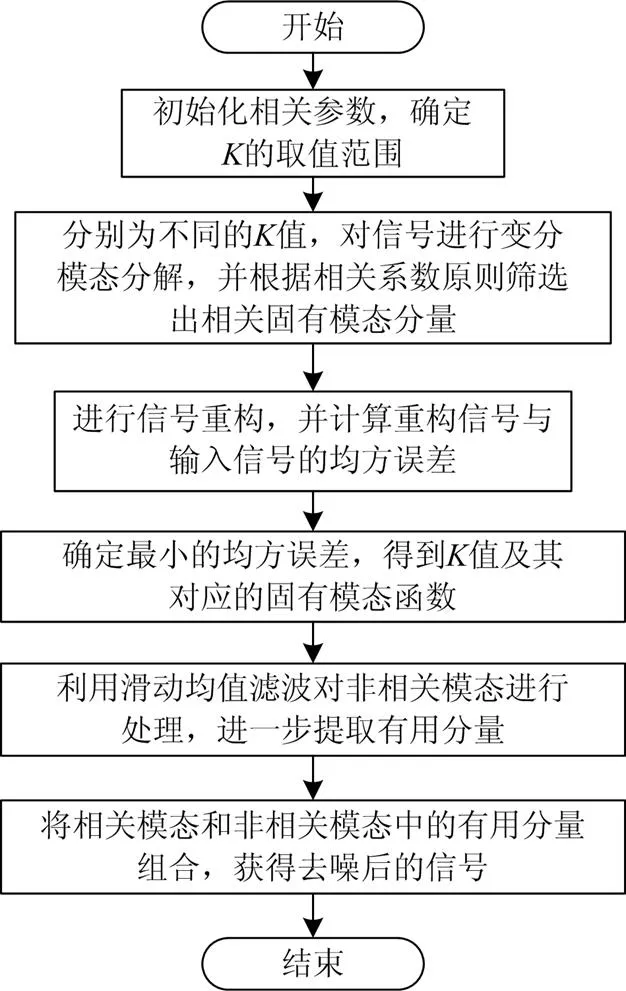
图3 算法流程图

3 算法性能检验

3.1 算例分析

1) EMD模态混叠问题的解决

分别利用EMD和VMD算法对0.2 s和0.6 s存在突变的信号进行分解，结果如图4、图5所示。

对比图4和图5可知，当信号含有间断时，EMD在IMF1就出现了模态混叠现象，而VMD则很好地将各个模态分量剥离开来，避免了模态混叠现象的发生。

图4 EMD分解结果

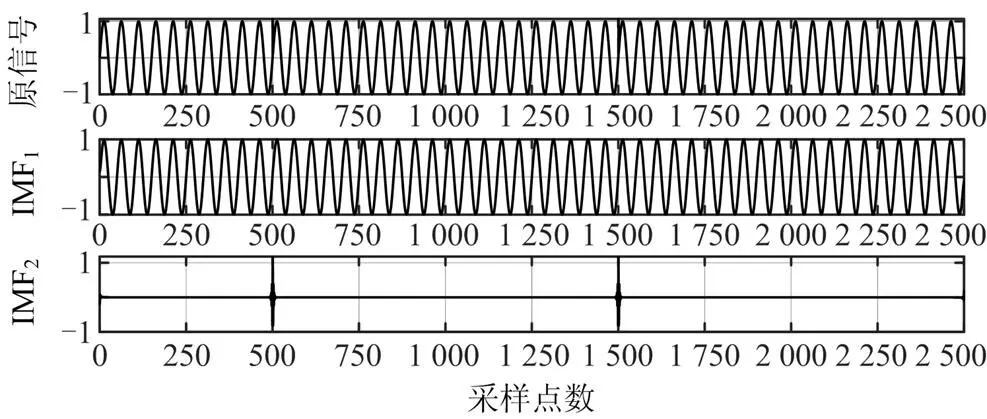
图5 VMD分解结果

2) 算法有效性检验

仿真生成正弦信号、电压暂降、电压中断、电压暂升、暂态脉冲、暂态振荡等6种电能质量信号，如表1所示，信号频率50 Hz，每周波采样64个点，共采样0.5 s，并加入信噪比为20 dB的高斯白噪声。

表1 电能质量扰动模型

使用本文所述去噪算法分别对这6种信号进行去噪处理，去噪结果如图6—图11所示。本文截取采样点数在500～1 000内的波形，从上到下分别为：添加20 dB白噪声后的含噪波形和利用本文算法去噪后的波形。

由图6—图11可以看出，本文所述方法能够有效地去除含噪波形中的噪声成分，重构波形与原信号波形基本一致，此外重构波形的突变点处的特征信息也得到了有效地保留，充分体现了本算法良好的去噪能力。

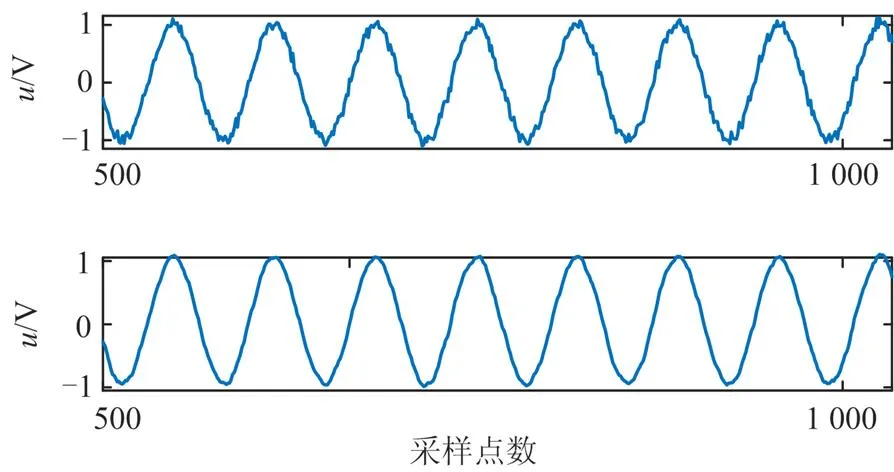
图6 正弦信号

图7 电压暂升

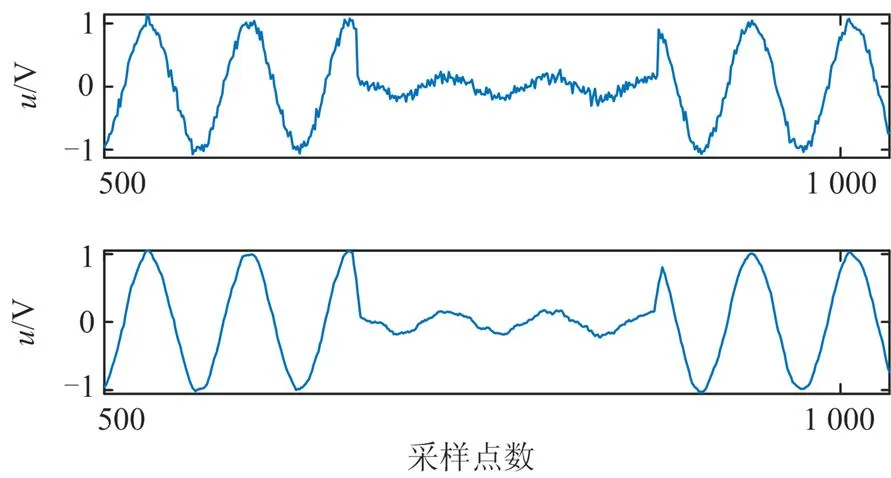
图8 电压暂降

图9 电压中断

图10 脉冲暂态

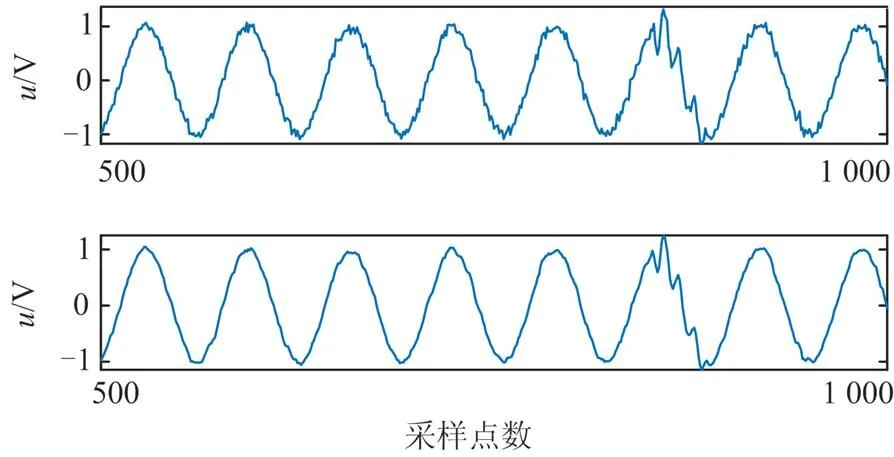
图11 振荡暂态

3.2 去噪效果对比分析

本文分别选取信噪比SNR和均方误差MSE作为去噪效果的评价指标。信噪比的计算公式为

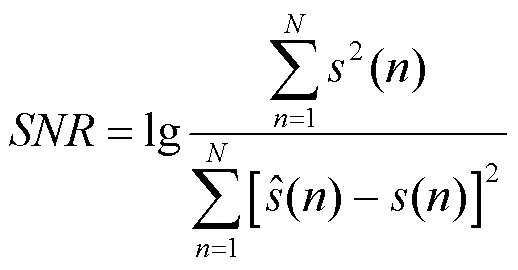
为了进一步说明本算法的有效性，分别利用本文提出的VMD去噪算法、文献[24]所述的EMD去噪算法以及文献[5]介绍的小波软阈值去噪算法对6种信号进行去噪，结果如图12、图13所示。其中选取db4小波作为小波去噪的小波基，根据基频和采样频率选取分解层数为4，阈值选取为通用阈值，其中σ为噪声的强度。

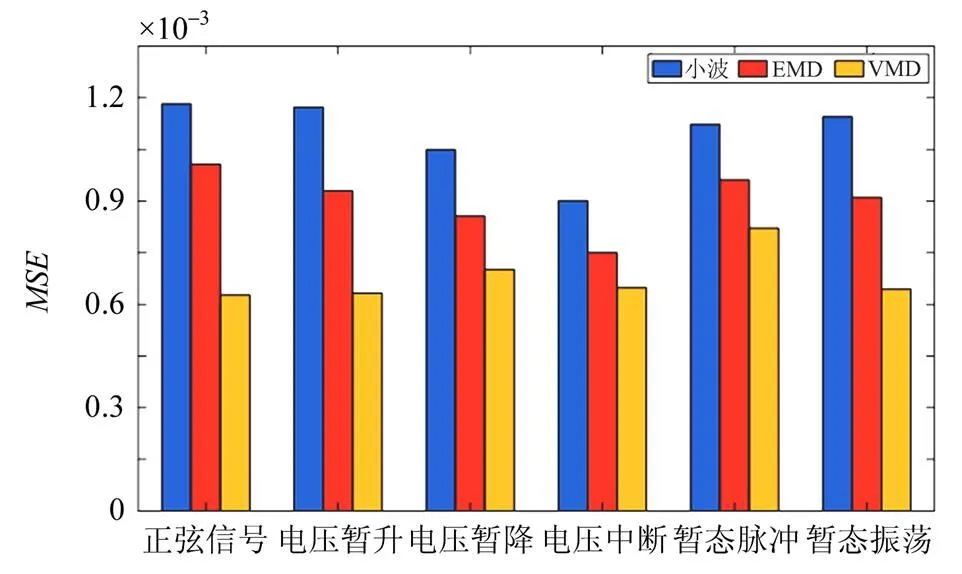
图13 去噪后MSE比较

由图12、图13可知，对于不同信噪比的输入信号，基于VMD去噪算法获得的去噪信号的SNR均高于小波去噪算法和EMD去噪算法，且MSE低于小波去噪和EMD去噪算法，充分说明了本方法的优越性。

此外，本文构造了信噪比为20 dB的暂态振荡电能质量扰动波形，综合比较了上述三种算法对于突变点特征的保留能力，去噪波形如图14所示。虚线框中表示振荡型瞬变的发生时期，从图中可以看出，基于VMD去噪算法获得的去噪波形突变点的幅值明显高于其他两种算法，且其幅值与加噪信号中的突变点的幅值基本保持一致，这有助于暂态扰动的检测以及后续的进一步分析。

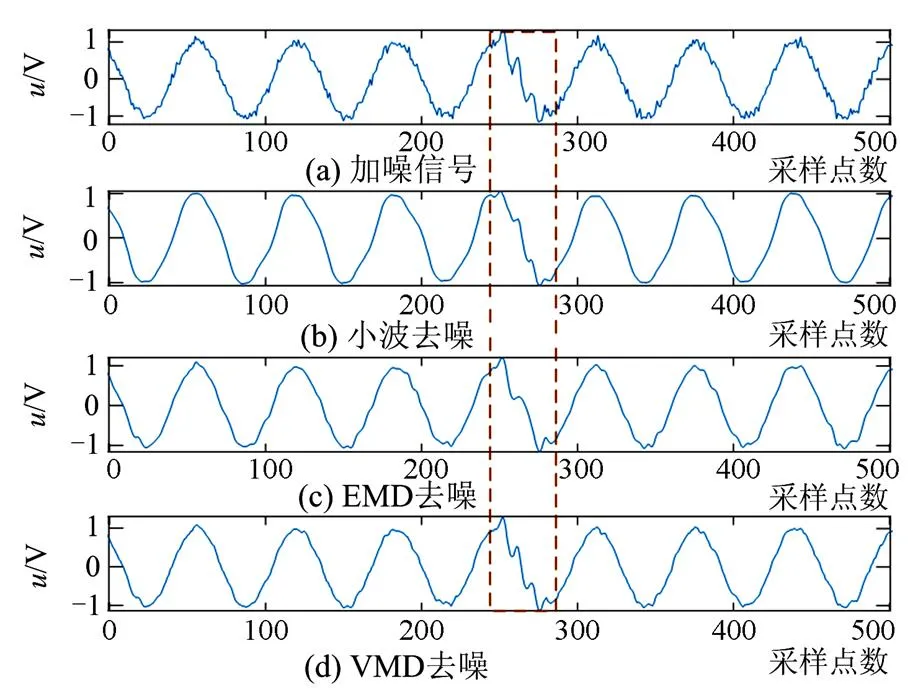
图14 去噪后波形整体效果比较

4 结论

针对经验模态分解去噪时存在的模态混叠问题，在变分模态分解原理基础上，建立了VMD与滑动均值滤波相结合的去噪算法及相关参数的确定方法，并通过仿真验证了所提算法的有效性。通过本文研究得出如下结论：

1) VMD通过控制固有模态函数的带宽可以克服EMD的模态混叠问题；

2) 通过相关系数和均方误差相结合的方法可以确定VMD合适的分解层数；

3) 通过对比分析，本文提出的去噪算法可以在更有效地去除暂态扰动中噪声的同时，保留暂态扰动中的特征信息。

[1] HUANG Li, YANG Yongbiao, ZHAO Honglei, et al.Time series modeling and filtering method of electric power load stochastic noise[J].Protection and Control of Modern Power Systems, 2017, 2(3): 269-275.

[2] MALLAT S, ZHONG S.Characterization of signals from multiscale edges[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(7): 710-732.

[3] PAN Q, ZHANG L, DAI G, et al.Two denoising methods by wavelet transform[J].IEEE Transactions on Signal Processing, 1999, 47(12): 3401-3406.

[4] 赵瑞珍, 屈汉章, 宋国乡.基于小波系数区域相关性的阈值滤波算法[J].西安电子科技大学学报, 2001, 28(3): 324-327.

ZHAO Ruizhen, QU Hanzhang, SONG Guoxiang.A threshold filtering algorithm based on the region relativity of the wavelet coefficients[J].Journal of Xidian University, 2001, 28(3): 324-327.

[5] DONOHO D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory, 1995, 41(3): 613-627.

[6] 欧阳森, 宋政湘, 陈德桂, 等.小波软阈值去噪技术在电能质量检测中的应用[J].电力系统自动化, 2002, 26(19): 56-60.

OUYANG Sen, SONG Zhengxiang, CHEN Degui, et al.Application of wavelet soft-threshold de-noising technique to power quality detection[J].Automation of Electric Power Systems, 2002, 26(19): 56-60.

[7] 谭莲子, 张莉萍, 解大, 等.改进小波阈值去噪法在谐波检测中的应用[J].电测与仪表, 2019, 56(13): 23-26, 75.

TAN Lianzi, ZHANG Liping, XIE Da, et al.Application of improved wavelet threshold de-noising method in harmonic detection[J].Electrical Measurement & Instrumentation, 2019, 56(13): 23-26, 75.

[8] 姚景岩, 杨世勇, 舒征宇, 等.基于航拍的输电线路覆冰厚度监测研究[J].高压电器, 2021, 57(8): 105-114.

YAO Jingyan, YANG Shiyong, SHU Zhengyu, et al.Research on monitoring of ice-coating thickness of transmission line based on aerial image[J].High Voltage Apparatus, 2021, 57(8): 105-114.

[9] 马星河, 张登奎, 朱昊哲, 等.基于EWT的高压电缆局部放电信号降噪研究[J].电力系统保护与控制, 2020, 48(23): 108-114.

MA Xinghe, ZHANG Dengkui, ZHU Haozhe, et al.Research on noise reduction of a partial discharge signal of a high voltage cable based on EWT[J].Power System Protection and Control, 2020, 48(23): 108-114.

[10]张全明, 刘会金, 周新启, 等.电能质量信号的小波软阈值去噪方法[J].高电压技术, 2006, 32(1): 99-101.

ZHANG Quanming, LIU Huijin, ZHOU Xinqi, et al.Wavelet soft-threshold denoising method of power quality signal[J].High Voltage Engineering, 2006, 32(1): 99-101.

[11]张明, 李开成, 胡益胜.基于小波邻域阈值分类的电能质量信号去噪算法[J].电力系统自动化, 2010, 34(10): 84-89.

ZHANG Ming, LI Kaicheng, HU Yisheng.A power quality signal denoising algorithm based on wavelet domain neighboring thresholding classification[J].Automation of Electric Power Systems, 2010, 34(10): 84-89.

[12]米翰宁, 王昕, 任广振, 等.自适应小波阈值去噪算法用于局部放电白噪声去噪[J].高压电器, 2021, 57(6): 94-101.

MI Hanning, WANG Xin, REN Guangzhen, et al.De-noising for white noise in partial discharge signals by adaptive wavelet threshold estimation[J].High Voltage Apparatus, 2021, 57(6): 94-101.

[13]吴童, 孙抗, 师文文.基于AVMD-自适应小波包法的电缆局部放电去噪研究[J].电力系统保护与控制, 2020, 48(14): 95-103.

WU Tong, SUN Kang, SHI Wenwen.Research on cable partial discharge denoising based on an AVMD-adaptive wavelet packet method[J].Power System Protection and Control, 2020, 48(14): 95-103.

[14]张大海, 杨宇辰, 刘艳梅, 等.基于EMD与Spearman相关系数的混合直流线路纵联保护方法[J].电力系统保护与控制, 2021, 49(9): 1-11.

ZHANG Dahai, YANG Yuchen, LIU Yanmei, et al.Hybrid HVDC line pilot protection method based on EMD and Spearman correlation coefficient[J].Power System Protection and Control, 2021, 49(9): 1-11.

[15]HUANG N E, SHEN Z, LONG S R, et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society, A, Mathematical, Physical, and Engineering Sciences, 1998, 454: 903-995.

[16]彭炜文, 刘伟杰, 许家浩, 等.一种基于相关系数的EEMD局部放电去噪方法[J].高压电器, 2021, 57(6): 203-209.

PENG Weiwen, LIU Weijie, XU Jiahao, et al.EEMD partial discharge de-noising method based on correlation coefficients[J].High Voltage Apparatus, 2021, 57(6): 203-209.

[17]秦代春, 刘强, 周林, 等.电能质量信号去噪方法研究[J].华东电力, 2009, 37(5): 767-772.

QIN Daichun, LIU Qiang, ZHOU Lin, et al.De-noising method for power quality signals[J].East China Electric Power, 2009, 37(5): 767-772.

[18]王俊, 李霞, 周昔东, 等.基于VMD和LSTM的超短期风速预测[J].电力系统保护与控制, 2020, 48(11): 45-52.

WANG Jun, LI Xia, ZHOU Xidong, et al.Ultra-short-term wind speed prediction based on VMD-LSTM[J].Power System Protection and Control, 2020, 48(11): 45-52.

[19]刘云凯, 彭显刚, 袁浩亮, 等.基于VMD与改进QRGRU的超短期风电功率概率预测[J].电力工程技术, 2021, 40(3): 72-77.

LIU Yunkai, PENG Xiangang, YUAN Haoliang, et al.Ultra-short-term wind power probability prediction based on VMD and improved QRGRU[J].Electric Power Engineering Technology, 2021, 40(3): 72-77.

[20]肖怀硕, 贾梧桐, 肖冰莹, 等.基于改进变分模态分解的低频振荡模式辨别[J].电力工程技术, 2020, 39(2): 95-102.

XIAO Huaishuo, JIA Wutong, XIAO Bingying, et al.An identification method for power system low-frequency oscillation based on parameter optimized variational mode decomposition[J].Electric Power Engineering Technology, 2020, 39(2): 95-102.

[21]钱国超, 彭庆军, 程志万, 等.基于参数自适应VMD和SA-ELM的有载分接开关故障诊断[J].电力工程技术, 2020, 39(1): 157-164.

QIAN Guochao, PENG Qingjun, CHENG Zhiwan, et al.Fault diagnosis of on-load tap-changer based on the parameter-adaptive VMD and SA-ELM[J].Electric Power Engineering Technology, 2020, 39(1): 157-164.

[22]赵海龙, 张丹丹, 黄松, 等.基于皮尔逊相关系数的海南省地闪密度与雷击故障关系分析[J].高压电器, 2019, 55(8): 186-192.

ZHAO Hailong, ZHANG Dandan, HUANG Song, et al.Analysis on the relation between cloud-to-ground lightning density and lightning trip rate in Hainan province based on Pearson correlation coefficient[J].High Voltage Apparatus, 2019, 55(8): 186-192.

[23]邵兴臣, 段发阶, 蒋佳佳, 等.基于自适应滑动均值和小波阈值的叶尖间隙信号降噪方法[J].传感技术学报, 2021, 34(1): 34-40.

SHAO Xingchen, DUAN Fajie, JIANG Jiajia, et al.Denoising method of blade tip clearance signal based on adaptive moving average and wavelet threshold[J].Journal of Transduction Technology, 2021, 34(1): 34-40.

[24]MERT A, AKAN A.Detrended fluctuation analysis for empirical mode decomposition based denoising[C] // 2014 22nd European Signal Processing Conference (EUSIPCO), September 1-5, 2014, Lisbon, Portugal.

Transient disturbance waveform denoising algorithm based on variational mode decomposition

ZHANG Minglong1, ZHANG Zhenyu1, 2, GAO Yuan1, LUO Xiang1, ZHOU Zhenyu3, ZHU Ke3

(1.Electric Power Research Institute, State Grid Fujian Electric Power Co., Ltd., Fuzhou 350007, China; 2.Key Laboratory of High Power Supply Reliability Distribution Technology of Fujian Province, Fuzhou 350007, China; 3.School of Electrical Engineering, Shandong University, Jinan 250061, China)

There is a problem of mode mixing in empirical mode decomposition (EMD) denoising.Thus a denoising algorithm combining variational mode decomposition and moving mean filtering is proposed.First, the noise signal is decomposed into several inherent modes by finding the optimal solution of the variational model.Then, the optimal decomposition layer K and its corresponding correlated modes are determined by the correlation coefficient criterion, and the uncorrelated modes are processed by the moving mean filter to get the useful components.Finally, the denoised signal is constructed based on the useful components extracted from the correlated and uncorrelated modes.Simulation results show that compared with EMD denoising and wavelet denoising, the proposed algorithm can effectively remove the noise in the transient disturbance while retaining the characteristic information in the transient disturbance.

transient disturbance; variational modal decomposition; correlation coefficient; sliding mean filtering; denoising

10.19783/j.cnki.pspc.210983

2021-07-29；

2021-08-31

张明龙(1976—)，男，硕士，高级工程师，研究方向为电力系统及其自动化；E-mail: 10446170@qq.com

朱 珂(1977—)，男，通信作者，副教授，硕士生导师，主要研究方向为状态监测，电能质量。E-mail: zhuke@ sdu.edu.com

国家电网有限公司总部科技项目资助“基于物联网技术的配电开关一二次深度融合与精益运维关键技术研究及应用”(52130421000S)

This work is supported by the Science and Technology Project of the Headquarters of State Grid Corporation of China (No.52130421000S).

(编辑 葛艳娜)