基于压电圆管的二维全向风能采集器研究

江雪玲，鲁彩江，2，李林峰，杨爱超，熊叮当，付国强

(1.西南交通大学机械工程学院，四川成都 610031；2.先进驱动节能技术教育部工程研究中心，四川成都 610031；3.国网江西省电力有限公司，江西南昌 330077)

0 引言

随着无线传感网络及微机电系统(MEMS)的发展，对无线传感器节点和微小设备的供能可靠性及稳定性提出了更高的要求[1]。传统电池供能方式存在能量有限、尺寸大、维护困难等缺点，无法实现长期可靠供电。环境能量采集技术通过将太阳能[2]、振动能[3-6]、风能[7-9]等转换为电能，实现设备的自供能，有望实现能源的持续性及清洁性。而风能作为自然界中广泛存在的清洁能源，对其的收集利用成为国内外研究的热点。基于风致振动效应的风能采集器主要包括涡激振动式[10-11]、颤振式[12]、驰振式[13]和尾流驰振式采集器[14]，是风能采集领域的主要方向之一，相比于旋转式结构，结构更加简单，易于集成化。风致振动能到电能的转换方式主要有压电[15-16]、电磁式[17]、静电式[18]，其中基于压电效应的风能采集器具有能量转换效率高、易于微型化等诸多优点，研究者对其展开了广泛的研究。

目前，关于风能采集器的研究主要致力于提升采集器的采集效率、拓宽有效风速范围、多向风能采集等方面。文献[19]利用磁感应非线性来提升采集器的性能。通过磁铁之间的排斥作用实现系统的双稳态特性。相比于线性能量采集器，双稳态设计显著提高了风能采集器的带宽。文献[20]通过引入非线性力并利用涡激振动和驰振之间的相互作用，有效拓宽了采集器的风速范围并提高其功率输出。文献[21]提出一种基于相互干扰的双压电阵列结构。放置在最佳相对位置的2个采集器的总输出功率是2个独立采集器总输出功率的2.2倍。文献[22]提出一种新型自感知式同步电感接口电路。该能量采集电路通过压电片输出的电压判断压电片的形变量，从而实现同步电感开关的自动控制。结果显示，新型采集电路可以输出比传统采集电路高30%的功率。

在多向风能采集方面，目前的相关研究还较少。在旋转式结构方面，文献[23]提出了基于撞击效应的多方向风能采集器，可用于电网的自供能无线传感器。采集器由S形转子、撞击棒、固定在主轴上的风向标、PVDF悬臂梁和储能模块组成。研究发现，采集器在20 kΩ负载和6.5 m/s的风速下，最大输出功率可达46.2 mW。采集装置的输出电压可以通过增加PVDF膜的数量来增加。但该旋转结构体积较大，不利于微型化。

在风致振动式结构方面，文献[24]使用弧形弹性梁设计了多方向、宽风速范围的风能采集器。该装置主要由弧形弹性梁、压电片和固定支撑结构组成。不同于传统采集器采用的矩形薄片悬臂梁，该采集器利用弧形弹性梁作为拾振结构，以响应风能并产生振动。其在不同方向、不同速度风的作用下将激发不同的振动形式，从而输出电能。弧形悬臂梁在一定程度上拓展了采集器的有效采集风向范围，而对于平面内其他方向的风能的采集效率却不高。文献[25]提出了交叉耦合的双梁结构，可以实现多方向的风能收集。 2个PZT压电梁交叉连接，一个圆柱体固定在下悬臂梁的自由端。上梁和下梁的锁定风速范围分别为0.59～1.69 m/s和1.82～4.0 m/s，极大提升了采集器的有效风速范围。但该采集器仅能实现平行于梁方向的风能的有效收集。

先前研究的多向风能采集器大多采用矩形薄片梁结构，仅能实现几个方向上风能的有效采集，环境适应性较差，不能完全响应并收集来自二维平面各方向的自然风。

为了解决传统风能采集器采集风向单一的问题，本文提出一种基于圆柱梁及压电圆管的多向风能采集器，该采集器采用细圆柱梁及末端圆柱钝体对平面各方向的风能进行响应，通过压电圆管将风致振动能量转换为电能输出。由于圆柱结构的对称特性，采集器对二维平面各方向的风均能做出响应并输出电能，具有很强的环境适应性。通过仿真与实验分析，验证了装置的全向性，为实际环境多向风能的采集利用提供了可行的研究方案，有利于推动风能采集器在无线传感网络及微机电系统(MEMS)中的应用。

1 采集器结构及其原理

1.1 采集器结构

本文提出的多向风能采集结构原理如图1(a)所示，采集器由圆柱钝体、圆柱梁、压电管等组成。圆柱钝体捕捉风能产生振动并传递给圆柱梁，圆柱梁弯曲变形产生应力应变，作用于压电管，压电管产生挤压变形，在正压电效应的作用下输出电能。压电管两极间连接电阻，通过检测电阻两端电压来观察采集器的输出。结构的风向示意图如图1(b)所示，当垂直于圆柱面的各方向的风作用于采集器时，由于整个装置为对称性结构，将产生相同的效应；可通过多组实验的方式来研究采集器在不同方向来流作用下的电压及功率输出。

1.2 工作原理及理论分析

当采集器置于流体环境中时，由于圆柱两侧的涡流脱落将产生涡激振动。涡流脱落频率与来流风速、斯特劳哈尔数以及钝体的特征尺寸有关，其关系可以表示为

(1)

式中：U为风速；fs为漩涡脱落的频率；S为斯特劳哈尔数，无量纲；d为圆柱钝体的特征尺寸，即直径。

漩涡脱落的频率fs与风速U呈正向关系；当fs与

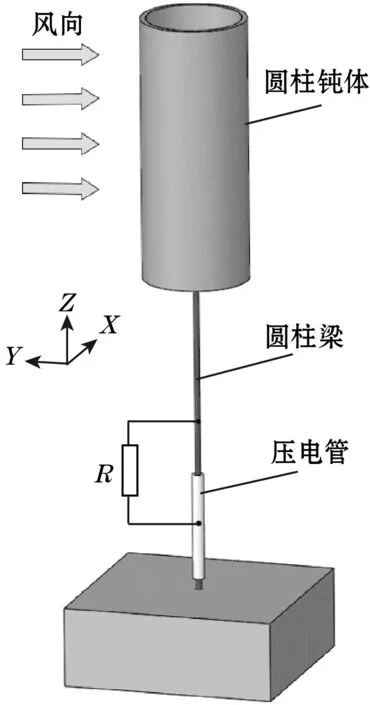
(a)采集器原理图

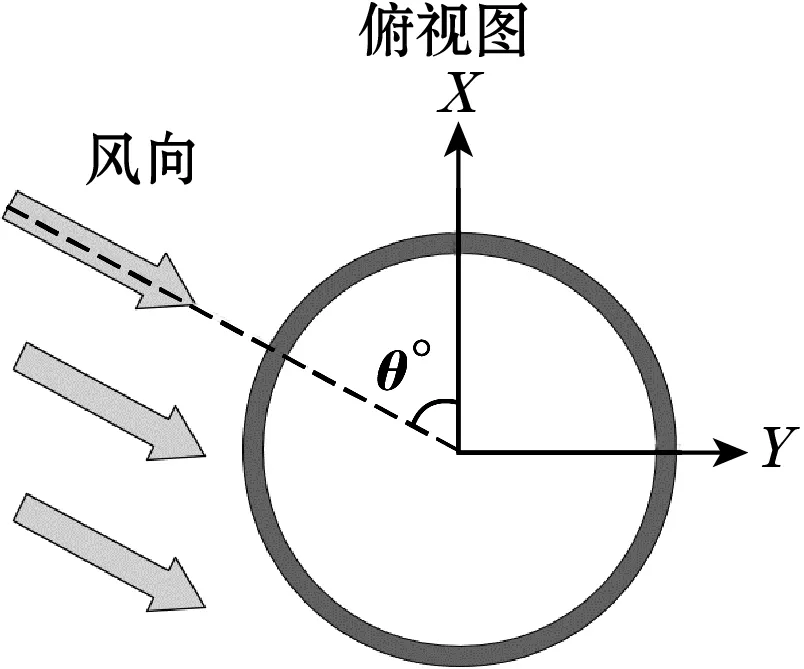
(b)风向示意图

结构的固有频率fn相等时，结构就会产生大幅振荡，发生涡激共振现象。而斯特劳哈尔数的变化则主要取决于雷诺系数：

(2)

式中：Re为雷诺系数；ρ为空气密度；μ为空气黏度。

传统的薄板矩形梁仅能在厚度方向弯曲振动，而细圆柱梁由于结构的对称特性，可沿径向各方向弯曲振动。当气流沿某一方向作用于系统时，采集器主要沿垂直气流方向横向振动，因此可采用集总参数动力学模型对其进行描述，如图2所示。

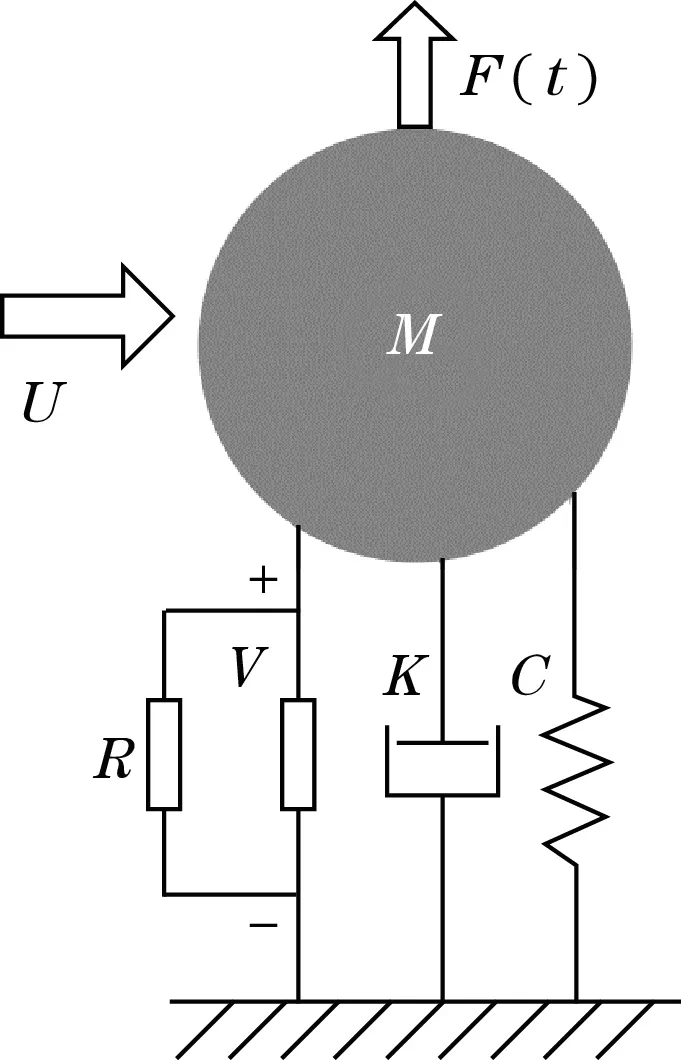
图2 压电风能采集器的弹簧-质量-阻尼器等效模型

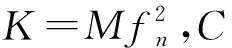
(3)

(4)

(5)

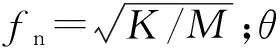
基于准稳态理论，气流作用于圆柱钝体上的空气动力可以表示为

(6)

式中：h为圆柱钝体的高度；Cd为平均阻力系数；CL为升力系数，CL=(CL0/2)q(t)；CL0为稳定升力系数。

由此可知，采集器的输出性能与漩涡脱落的频率、电阻、风速大小、圆柱尺寸、等效质量等相关。可进一步优化数学模型，通过确定系统的固有参数，根据公式得到系统输出电压及功率与各变量之间的关系。对于给定圆柱(定尺寸、定质量)，接下来将通过仿真研究采集器输出性能与频率、负载电阻、激励力(风力)的关系。

1.3 仿真分析

采用COMSOL Multiphysics软件研究多向风能采集器的特性。建立三维模型，通过耦合固体力学、静电场和电路进行有限元分析。在仿真中，模型与采集器原型的尺寸相同。固定约束添加在模型的底部。激励力沿Y轴，并可以视为风力。压电管沿径向极化，并连接有电阻。采集器的前两阶模态分析如图3所示。由于采集器的对称性，结构的一阶和二阶固有频率均为15.06 Hz。

对采集结构进行了频域扫描，频率范围为10～20 Hz。不同频率下，采集器的输出电压与电功率随频率的变化规律如图4(a)所示。在固有频率(15.0 Hz)附近，可获得较大的输出。

然后进行了频域研究，采集器工作频率为15.0 Hz，研究不同负载作用下，结构输出电压及电功率的变化。如图4(b)所示，电压和电功率随电阻变化而变化，并且存在最佳电阻使输出最大化，约为3.16 MΩ。仿真分析了激振力对采集器输出的影响。越大的激振力对应越大的风速。如图4(c)所示，电阻的输出电压和功率随激振力的增加而增加。

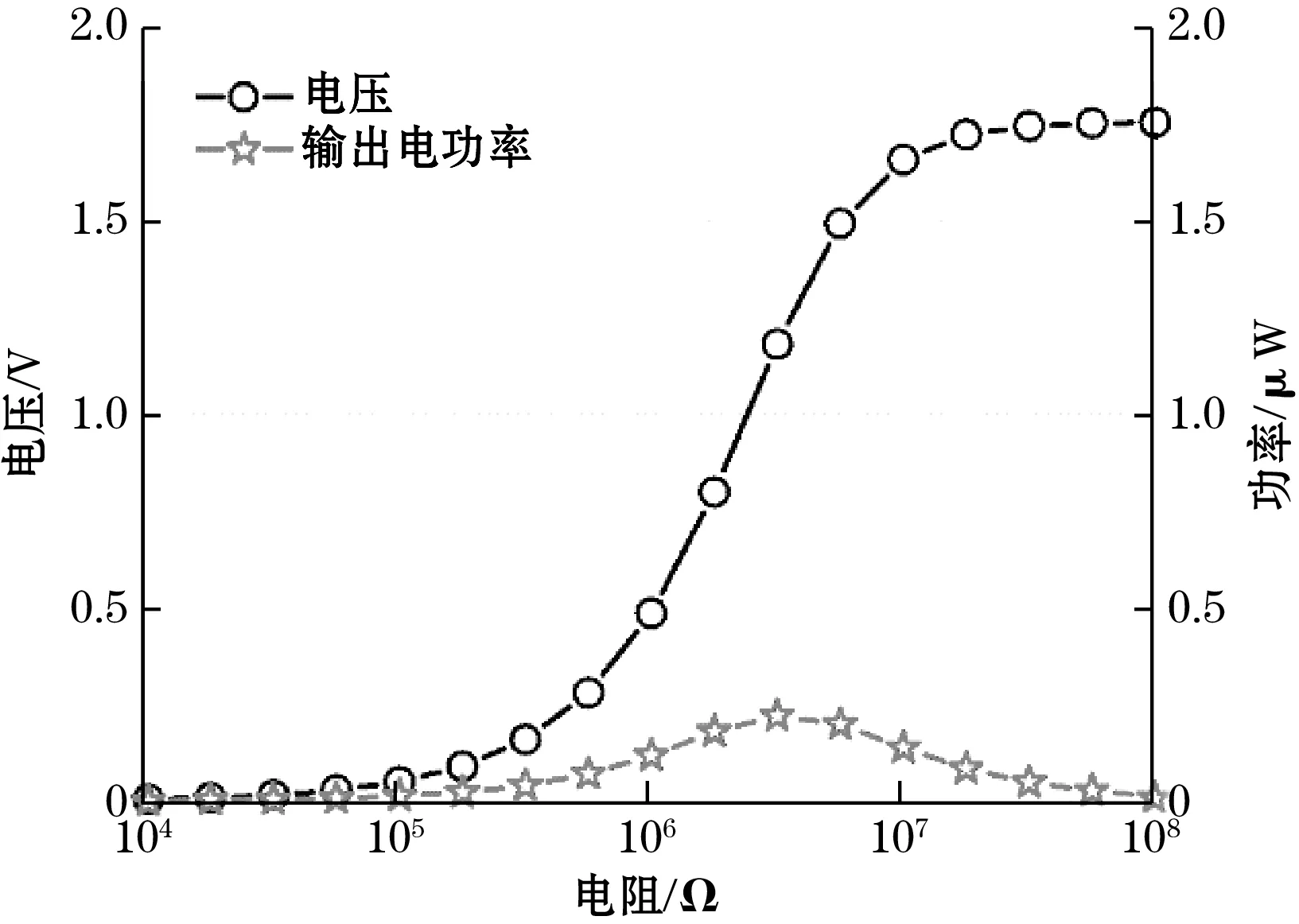
(b)输出随电阻的变化规律

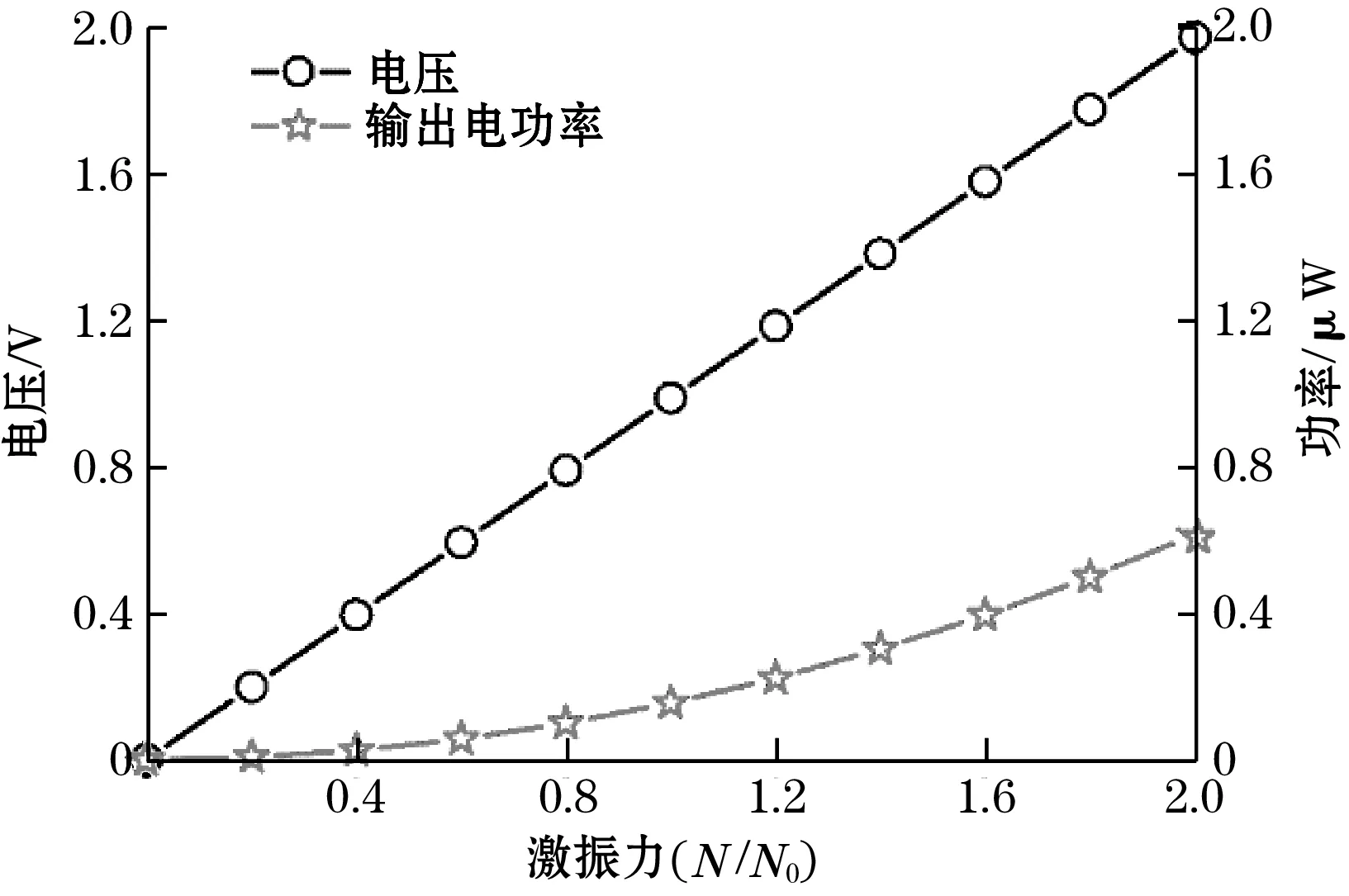
(c)输出随激振力的变化规律图4 仿真结果分析

2 样机制作与实验系统

2.1 采集器样机制作

圆柱悬臂梁的材料为Fe-Ga合金材料，直径为1 mm，长度为60 mm。圆柱钝体直径为20 mm，长50 mm，采用空心结构以增加采集系统的振动频率；压电圆管采用PT120.0压电陶瓷管(电容为3 nF)，其压电陶瓷类型为PIC151，性能优异，压电效应好，内径为1 mm，外径为2.2 mm，长20 mm，如图5(a)所示。压电圆管沿径向极化，内外电极间连接电阻R。压电圆管通过粘胶固定在圆柱梁的下端，在梁弯曲振动过程中受到更大的应力，输出更高的电压。

圆柱梁作为内部电极的导电体。 压电圆管显示出较高的压电电荷系数：d33=500×10-12C/N，d31=-210×10-12C/N。 压电管工作方式为d31模式，即沿压电管的厚度方向产生电压，而应变沿压电管和圆柱梁的轴向，因此，在输出性能提升方面，d31系数起着更为重要的作用。此外，圆柱体是中空的，减轻了结构的质量，从而使采集器的频率增加了。整个采集器原型结构如图5(b)所示。

图5 压电圆管及采集器实物

2.2 实验测试系统

实验中，风力由小型风洞测试系统提供，如图6所示。风洞截面为32 cm×32 cm。采用变频器控制风机转速从而控制风速大小。通过热线式风速仪(TES-1341)测量风速。采集器底部固定在夹具上，为了防止压电管的损坏，使压电管距离夹具上表面1 mm。压电圆管内外电极间连接电阻箱，数字示波器(TBS1102B)测量并保存电阻两端的输出电压。低噪声前置放大器连接于采集器终端和示波器之间，以衰减输入信号。

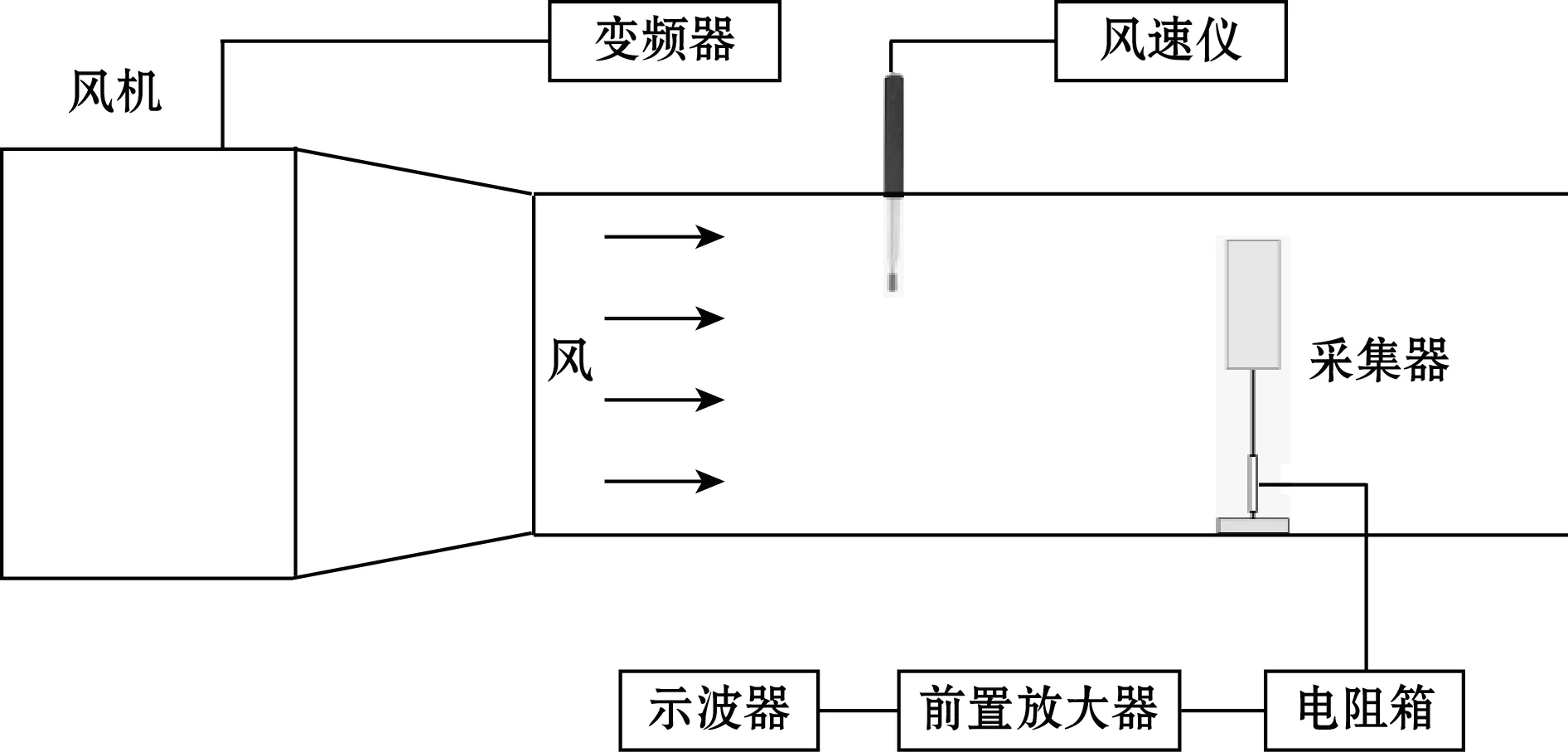
(a)风洞测试系统框图

(b)风洞测试平台图6 风洞测试系统

3 实验结果与分析

3.1 最优电阻

图7中绘制的曲线显示了当风速为6 m/s和7 m/s时，采集器输出的均方根(RMS)电压和平均功率随负载电阻(0.05～5 MΩ)的变化规律。平均收集功率的计算公式为

(7)

式中VRMS为负载电阻R两端的RMS电压。

图7 风速为6 m/s、7 m/s时，采集的RMS电压 和功率与电负载的变化关系

由图7可知，RMS电压随着负载电阻的增加而增大；输出功率随着负载电阻的增加先增大后减小，在R=2.2 MΩ时，获得的功率最高。最佳负载电阻是指：同一风速下，风能采集器输出最大功率时的外部负载电阻，且该阻值几乎不随风速变化而变化。在6 m/s和7 m/s的风速下，采集器均在阻值为2.2 MΩ左右取得最佳输出，因此，R=2.2 MΩ被认为是本研究的最佳负载电阻，并运用于接下来的实验中。

实验和仿真得到的最佳负载电阻分别为2.2 MΩ和3.16 MΩ，存在一定的差异。主要是因为仿真时仅考虑了压电管的静态电容，而忽略了其动态电容和电感，且仿真时给定体载荷与真实气流场的作用力存在差异。

3.2 输出性能

实验研究了采集器在不同风速下的输出性能。图8是风速为4、5、6、7、8 m/s时的电压波形图。由图8可知，输出电压随着风速增加呈增大趋势。当风速达到8 m/s时，可获得约3.5 V的峰值电压。

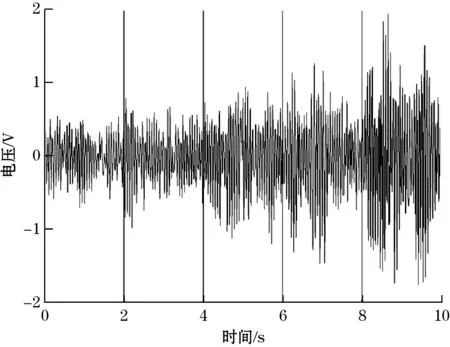
图8 4～8 m/s风速下的电压波形

图9是风速为6.5 m/s和8 m/s时采集器输出电压波形的快速傅里叶变换。由图9可见，输出电压的优势频率约为16.5 Hz，且基本不随风速变化而变化。由于圆柱梁结构振动的不稳定性，电压的幅频特性曲线在采集器固有频率附近存在波动，但仍在固有频率处获得最大振幅。由于仿真与实验环境存在差异，且未考虑夹具、运动不稳定性的影响，仿真所得固有频率与实验振动频率有较小的差距。

3.3 采集性能

为了研究采集器输出电压(RMS电压)和功率随风速的变化规律。在1～8 m/s的风速下，测试了采集装置的输出性能，结果如图10所示。采集器的切入风速在2.5 m/s左右，且其输出电压和功率随着风速的增大而增加。在8 m/s的风速下，该装置可产生0.262 μW的功率。由此可见，在更高风速条件下(8 m/s以上)，采集器有望获得更高的功率输出，有利于促进其实际应用。

由于结构的对称性，平面各方向的风作用于采集器时，将会产生相同的效应，因此可通过多组实验方式验证其二维全向性。风速为8 m/s时，采集器输出功率随风力方向的关系如图11所示。由图11可知：采集器可实现整个二维平面(0～360°)内风能的有效采集；在8 m/s的风速下，可产生0.26～0.27 μW的功率。因此该采集器具有二维全向性能，在更高风速下可实现更大的功率输出。

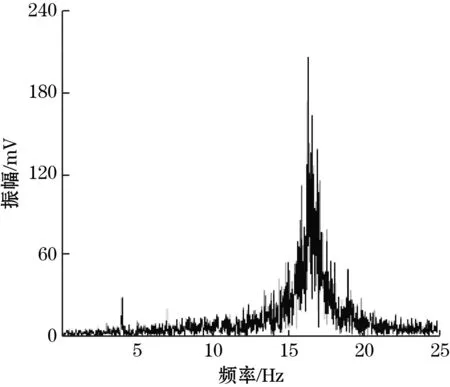
(a)6.5 m/s

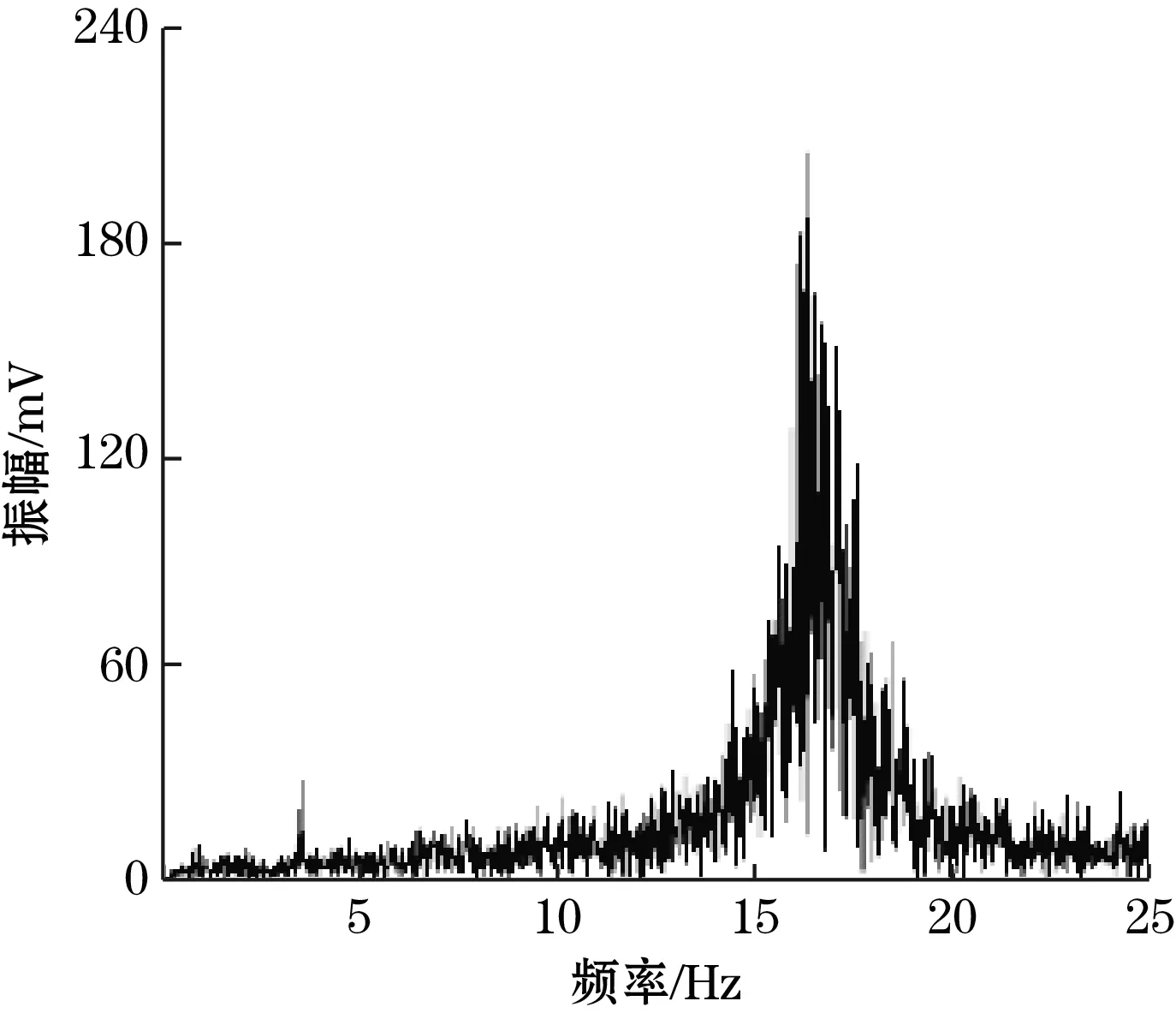
(b)8 m/s图9 6.5 m/s和8 m/s风速下电压的幅频特性

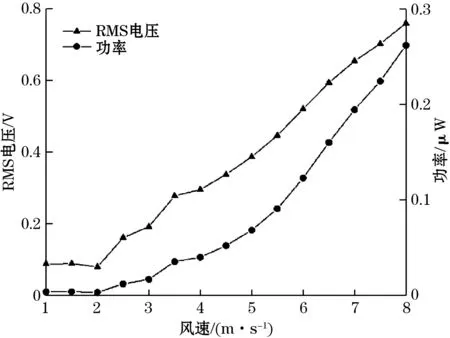
图10 采集器输出电压和功率随风速的变化规律

图11 8 m/s风速下，采集器输出电功率随风向的变化规律

4 结论

本文针对现有风能采集器采集方向单一的问题，提出一种基于压电圆柱梁的多向风能采集器。可对二维平面各方向的风能进行有效采集。采用细圆柱梁代替传统薄片矩形梁，实现多向风的响应；带圆柱钝体的采集器在气流作用下，将产生涡激振动，通过压电圆管将风致振动能量转换为电能输出。搭建了小型风洞测试系统对所设计的多向风能采集器进行实验研究。分析结果表明，采集器的输出功率随着风速的增加而增大，其风能采集范围扩展到了整个二维平面，即有效采集角度范围为360°，且具有较宽的有效风速范围。当风速为8 m/s时，负载电阻为2.2 MΩ时，该装置在二维平面任意方向气流作用下均可获得约0.26 μW的功率。电子学的进步促进了低功耗电路的出现，也使得环境能量采集技术的实际应用变得可行。所提出的采集器具有结构简单、体积小、环境适应性强等优点，有利于促进风能采集器在自供电在线检测等领域的实际应用，为多向风能的收集利用提供了方向。未来的研究中，可以通过增加采集器数量形成阵列式结构，以提升整个风能采集系统的采集效率。