运用图像轨迹规划的无标定机器人视觉伺服控制

黄正军，王桂锋，施卢丹

（金华职业技术学院，浙江金华 321017）

随着人工智能及机器人技术的迅猛发展，机器人执行任务的复杂性和多样性不断提高，具备感知能力、能与外界互动的智能机器人被公认为今后机器人发展的方向[1]。机器人视觉伺服系统利用视觉信息作为控制反馈控制机器人关节运动，具有信息量大、适用范围广等特点，可以克服模型中存在的不确定性，提高机器人定位或跟踪的精度[2-5]。传统的机器人视觉伺服系统的性能高度依赖于标定精度[6]，但视觉伺服系统的标定精度受相机畸变以及图像噪声等诸多因素影响[7-9]，所以无标定视觉伺服作为一种新的视觉伺服形式逐渐成为机器人伺服控制系统重要的发展方向和研究热点。

根据反馈的控制误差的不同，机器人视觉伺服控制可分为基于位置的视觉伺服（PBVS）和基于图像的视觉伺服（IBVS）[10]。相较于PBVS，IBVS因无需对目标位姿三维重建，计算量较小而得到广泛关注[11-13]。刘晓玉和方康玲[14]介绍了IBVS的原理和基本实现方法，并详细阐述了图像特征的提取。文献[15-16]利用神经网络法实现机器人的无标定视觉伺服控制，但神经网络法必须进行大量的样本学习，算法较为繁琐复杂、计算量大。路清彦等[17]用几何形状检索CAD三维数据模型，对图像信息中相关特征进行交互，并从背景中分离出目标物体，从而实现机器人的定位与目标抓取。但该方法仅对轮廓明显且具有反光特性的目标具有较好的识别能力，且事先需要建立目标的三维模型，然后通过迭代算法将三维模型与图像中目标物体的边缘进行不断拟合，计算量大。钱江和苏剑波[18]通过研究在线估算图像雅可比矩阵来实现无标定机器人视觉伺服控制，但仅限于二维运动。

针对单目手眼机器人视觉伺服控制的问题，本文研究了一种基于图像轨迹规划与时序控制的无标定视觉伺服控制方法。首先，给出了雅可比矩阵及其逆矩阵的推导过程。其次，介绍了目标图像特征及相对应的相机运动的轨迹规划方法，以实现机器人的时序控制。再次，针对单目视觉系统中目标深度未知的问题，设计了卡尔曼滤波器估算目标与相机相对位姿，结合相机测量实现了雅可比矩阵的自适应估算。从次，在此基础上设计了基于图像视觉反馈的视觉伺服控制器，实现了7自由度无标定机器人的视觉定位与跟踪。最后，通过仿真实验验证了本文算法的可行性。

1 图像雅可比矩阵

在基于图像的视觉伺服中需要把图像特征的变化转化为机器人末端的位置变化，这种变换关系通过图像雅可比矩阵实现。设目标物体上任一特征点P在相机坐标系中的坐标为(c)Xp=[Px Py Pz]T，在图像平面的坐标为(s)s=[sx sy]T。根据针孔相机的成像模型有

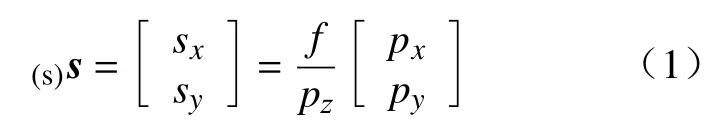
式中f为相机的焦距。

当物体处于静止状态，相机在机械手的带动下运动时，(s)s仅和相机在相机坐标系中的位姿(c)X有关。目标图像特征的运动速度(s)s˙和相机运动速度(c)X˙ 之间的关系为

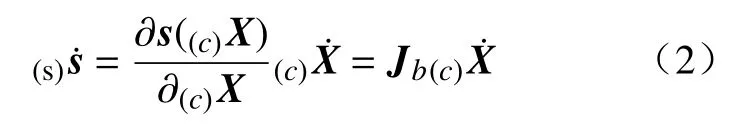
式中：Jb∈R2×m称为图像雅可比矩阵，m为任务空间维数，空间运动时m=6；目标特征点数目为N时Jb∈R2N×m。对单个目标特征点其图像雅可比矩阵的计算方法为

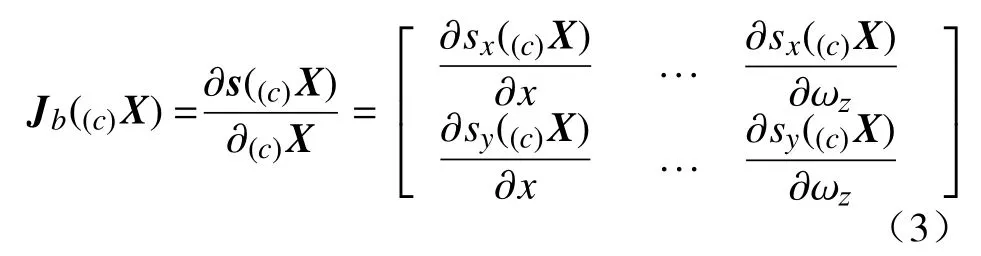
把式（1）代入式（3）并把特征点(c)Xp=[Px Py Pz]T的变化表述为相机的运动变化，则有

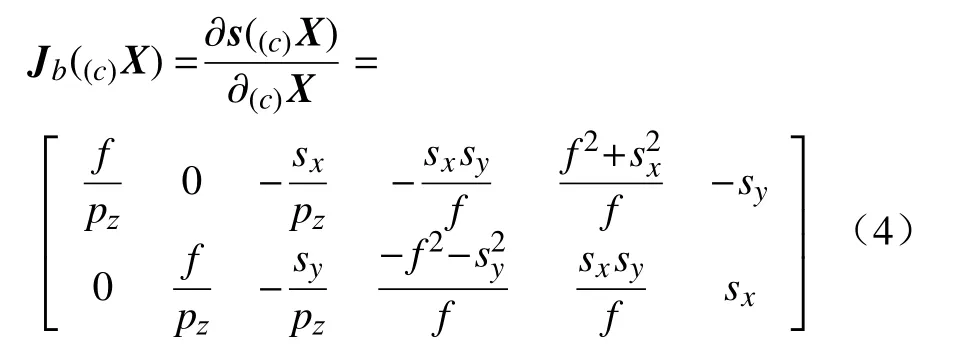
图像雅可比矩阵由Weiss首先提出，又被称为特征敏感度矩阵，文献[19]给出了其详细推导过程。

为实现机器人视觉伺服控制，需要由图像特征变化率(s)s˙计 算相应的相机运动速度(c)X˙，为此需求图像雅可比矩阵的逆矩阵，在2N=m的情况下有

为实现目标位姿的三维重构，至少需要任务空间维数一半的特征点，空间运动情况下即3个特征点。考虑到算法的鲁棒性往往需要更多的目标特征点，本文选用4个特征点来重构目标位姿，在此情况下图像雅可比矩阵不能直接求逆。采用最小二乘法求其伪逆矩阵可得

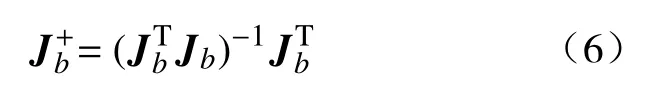
则相机运动速度计算公式为

在公式（7）的基础上引入一个放大系数kp就构成了一个简单的P-控制器。

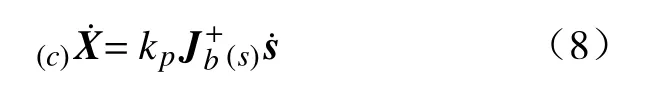
2 图像平面及任务空间的轨迹规划

在期望图像特征及控制器放大系数不变的情况下，在伺服控制开始阶段目标实际图像特征离期望图像特征距离较远，图像误差较大，由此产生的相机运动速度大，机器人运动剧烈；而在伺服控制末期目标实际图像特征接近期望图像特征，图像误差微小，相机运动速度慢，机器人运动微弱。这降低了伺服控制的效率，同时也不利于估计伺服控制时间。

为解决上述问题，需离线规划目标图像特征的运动轨迹及相应的相机运动。相机在任务空间的运动轨迹可以在考虑关节运动局限的前提下通过插值法获得，并据此计算相应的图像轨迹，计算出来的图像特征向量作为时序控制的期望值。这种方法相比传统的视觉伺服控制具有更高的鲁棒性，同时改善了伺服控制的效率及伺服过程的可预见性。由于微小的图像特征变化即可导致剧烈的相机运动，轨迹规划时需在考虑关节运动局限的前提下改变控制器放大系数。假设相机在任务空间的运动局限为

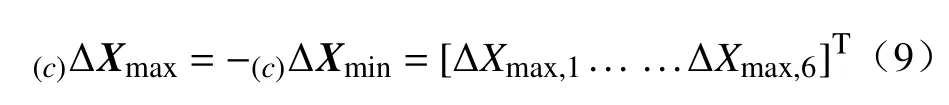
结合公式（8），k时刻的相机运动可表达为

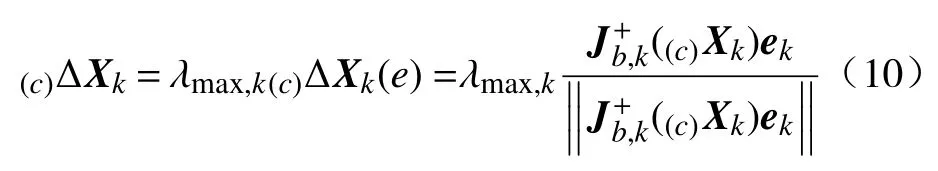
式中ek=sd,k−si,k为k时刻目标特征点的期望图像特征与实际图像特征之差。

k时刻的放大系数选择应使相机运动满足

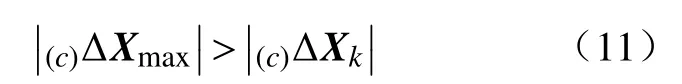
此外为避免相机过摆还需满足

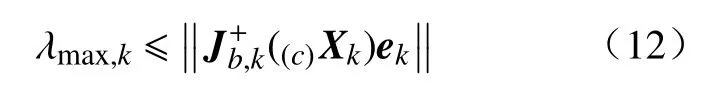
综合上述条件k时刻的放大系数可通过以下方法选择

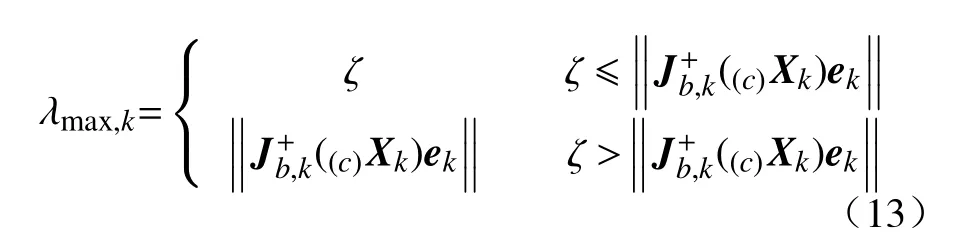
其中

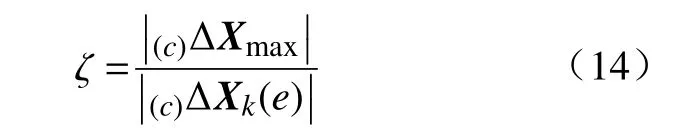
假设k时刻目标特征点在相机坐标系中的位姿为(c)，则k+1时刻的位姿为

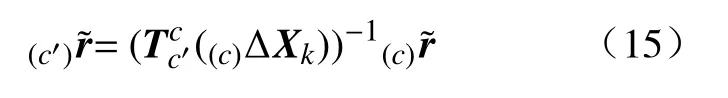
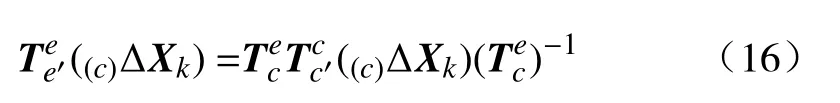
由于手眼系统中相机和末端执行器的方位关系不变，且相机通过公式（9）保持缓慢运动，因此可以认为末端执行器运动缓慢。那么其在机器人坐标系中的微量变换可表示为：

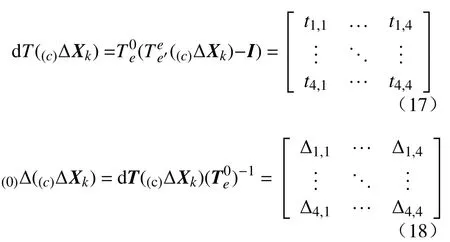
由于(0)Δ((c)ΔXk)的旋转部分为描述微小转动的斜对称矩阵，公式（18）所示的微量变换也可通过微量位移向量表达，即

k时刻末端执行器在任务空间的轨迹为

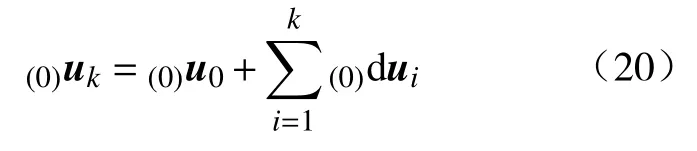
通过该方法得到末端执行器在任务空间的运动轨迹及相应的图像特征。适合于机器人运动的图像平面运动轨迹可利用以上轨迹参数并考虑机器人关节运动限制通过插值法求得。设b和a分别为(0)uk+1和（(0)uk′−(0)uk）的欧几里得范数，基于式（2）的线性关系，每一步的图像特征轨迹通过以下插值规则求得

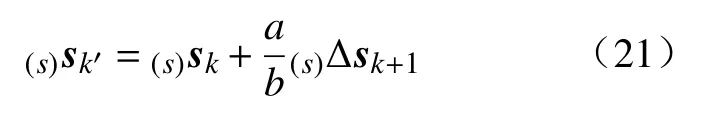
式中：(s)Δsk+1=(s)sk+1−(s)sk为由任务空间轨迹规划得到的k时刻的图像特征变化；(s)sk′为规划的适合于机器人运动的图像平面特征。

通过以上方法得到了图像平面的期望运动轨迹。为了计算作为控制输入的图像误差需要实际的图像特征信息，但由于图像处理的速率比控制器要求的慢，不能在所有时刻都有更新的图像信息。为了减少图像误差的跳跃变化，需要引入外插法估计没有相机数据时刻的图像信息。设Tf为控制器采样时间，T为图像处理采样时间，则k时刻的实际图像特征信息估计为

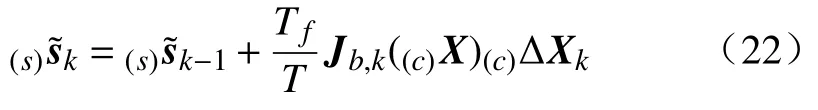
每当有相机测量数据更新时利用测量数据替代估计值，即

3 扩展卡尔曼滤波器的设计

从公式（4）可以看出，图像雅可比矩阵不仅和图像特征向量有关，还和目标与相机距离有关。针对单目视觉系统中目标深度未知的问题，本文设计了一个卡尔曼滤波器来估算目标相对相机位姿，以实现雅可比矩阵的在线估算。

3.1 状态方程的建立

定义系统状态向量为

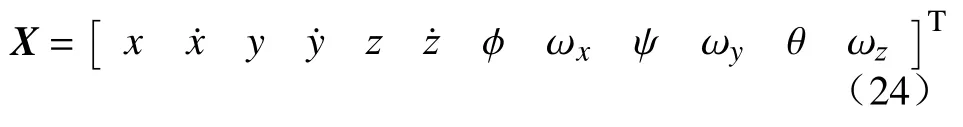
式（24）中前6个分量描述目标的平移运动，后6个分量描述目标的旋转运动。卡尔曼滤波的系统状态方程为

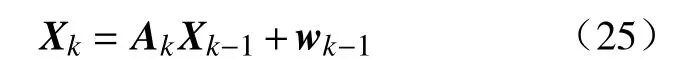
式中：A为系统矩阵；wk−1为零均值系统高斯白噪声，其协方差阵为Qk−1。假设相机运动缓慢并且在每一个采样周期内速度不变，则系统矩阵A为

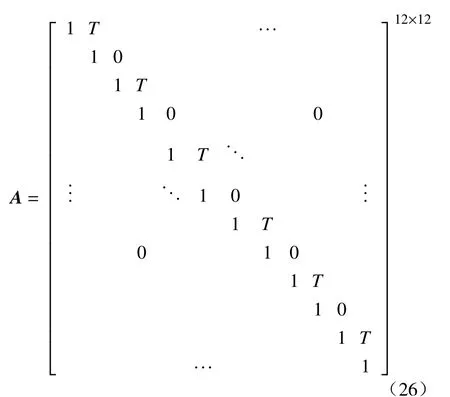
3.2 观测方程的建立

取目标特征点的图像特征向量作为观测向量，建立扩展卡尔曼滤波器的观测方程为

式中：sk为目标特征点的图像特征向量，为保证位姿估算的鲁棒性，采用4个特征点来估算目标相对相机位姿；G(Xk)为描述相机成像模型的函数。对于普通针孔相机其图像平面的像素坐标计算如下：

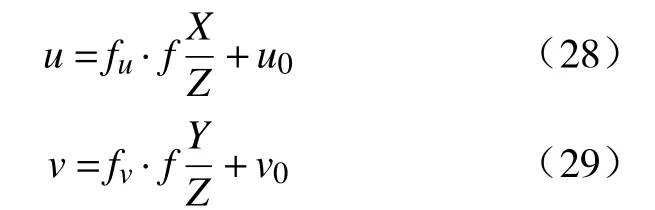
式中：u、v为特征点在图像平面的像素坐标；X、Y、Z为特征点在相机坐标系中的坐标；f为相机焦距；fu、fv分别为图像平面上X和Y轴方向单位距离像素数；u0、v0为图像平面中心坐标。

结合式（28）、（29）观测方程表达式为

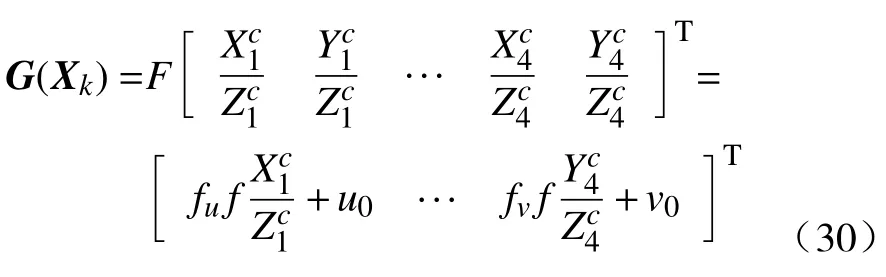
3.3 扩展卡尔曼滤波算法步骤

本文设计的扩展卡尔曼滤波算法如下：

1）对状态向量以及方差进行初始化，给定初始值。

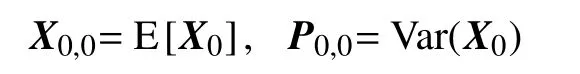
2）计算状态向量及协方差的初步预测值

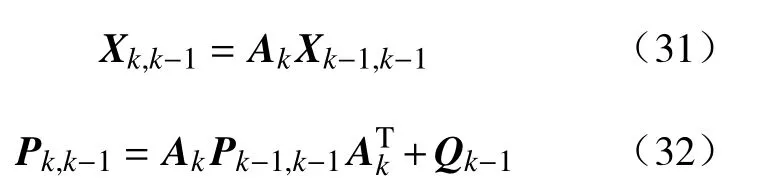
3）计算量测矩阵（线性化处理）

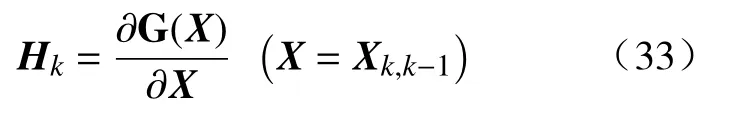
4）计算卡尔曼增益

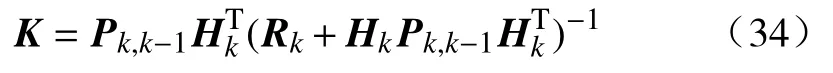
5）根据卡尔曼增益及观测向量更新估计值

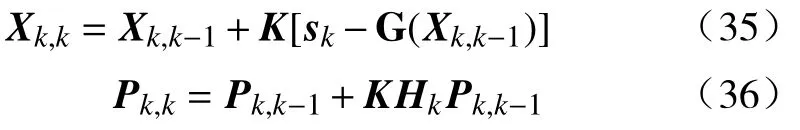
6）令k=k+1，重复上述步骤。

估算位姿中的目标深度信息用于图像雅可比矩阵的在线估算。

4 视觉伺服控制框架设计

基于图像轨迹规划的机器人视觉伺服控制系统框图如图1所示。

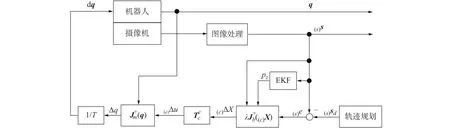
图1 视觉伺服控制结构框图

由轨迹规划获得特征点的期望图像特征向量为(s)sd，由摄像机测量的实际图像特征向量为(s)s，则在图像平面定义的图像特征误差为

利用相机测量的实际图像特征向量及EKF输出的目标深度信息，根据公式（4）计算图像雅可比矩阵更新，然后根据公式（8）计算相机相对于相机坐标系运动，表达式为

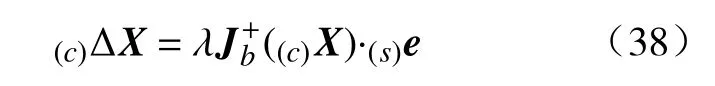
式中λ为控制器放大系数。

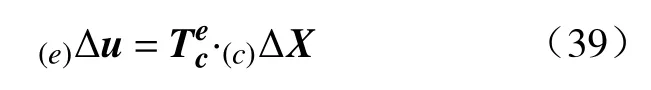
通过机器人逆运动学由末端执行器运动计算各关节运动，表达式为

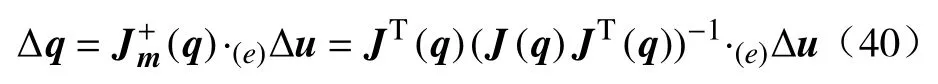
式中：J(q)∈Rm×n为机器人雅可比矩阵；m为任务空间维数；n为机器人自由度。

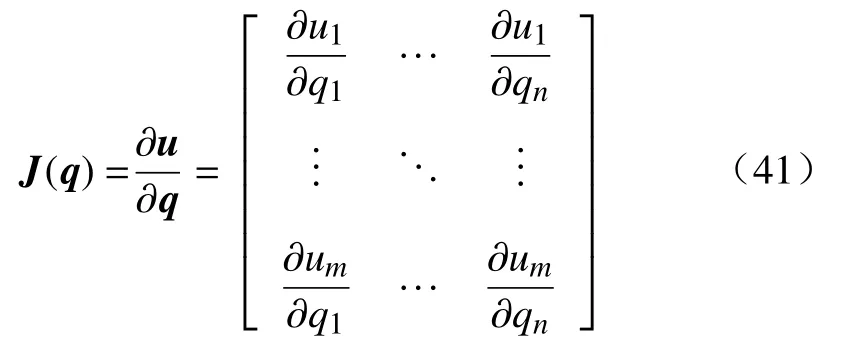
由关节运动计算各关节角速度，表达式为

5 MATLAB/SIMULINK仿真及实验研究

在MATLAB环境中建立手眼机器人视觉伺服系统仿真模型，以图2所示的7自由度机器人视觉伺服系统为研究对象，对目标跟踪过程进行仿真。

图2 手眼机器人视觉伺服系统

伺服任务定义为：以A4纸打印4个墨点为定位特征，机器人末端执行器做空间运动，使之位于特征点正前方，特征点图像特征与给定期望特征重合。

仿真参数设置如下：相机焦距f为8.05 mm，X轴方向单位距离像素数为86.65，Y轴方向单位距离像素数为86.25。

相机固定在机器人末端上方，其定位关系设定为

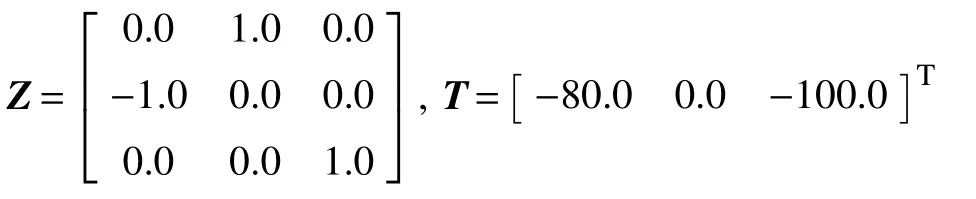
各关节起始角弧度为 [0，−0.8677，0，−1.5188，0，−1.2444，−0.1764]T，初始图像特征为s(0)=[180.7，60.5，236.5，74，203.6，150.6，146.7，112.3]T，期望图像特征为sd=[188，235，209，241.6，197，276，174，258]T。 EKF 初 始 参 数 为 ：P0= 0.2∗eye(12,12)，Q=diag(ones(12,1)*0.06)，R=diag(ones(8,1)*0.000006)，X0=zeros(12,1)。控制器放大系数设定为λ=0.08，系统采样时间为50 ms，在图像平面添加零均值、最大为3个像素的观测噪声。图像平面特征点的仿真跟踪轨迹如图3所示，相应的机器人关节角度变化如图4所示。

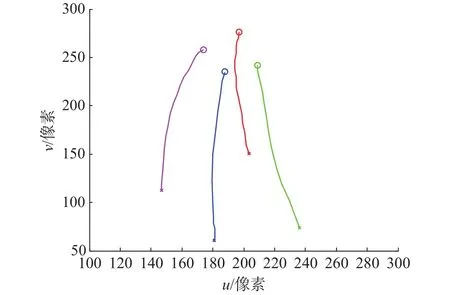
图3 图像特征仿真跟踪轨迹

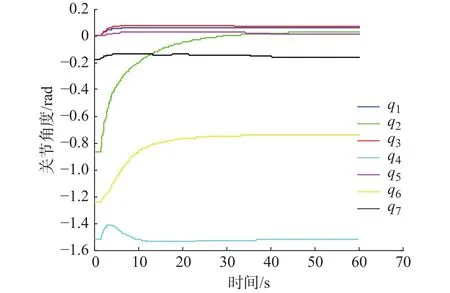
图4 机器人关节角度变化

从图3可知，图像特征轨迹以近直线方式从初始位置收敛到期望位置，保证了视觉伺服的效率，且特征点始终保持在相机视场范围内。从图4可知，除了第 2、6 关节有较大转动外（约 0.9 rad 和 0.5 rad），其余关节的转动量都很小（不超过0.1 rad），机器人各关节运动平缓，降低了伺服过程的能量消耗。

为验证本文算法的有效性，以经典PBVS和IBVS方法为比较对象，把通过仿真模型验证的视觉伺服算法植入图2所示的机器人视觉伺服系统中，对目标跟踪过程进行实验验证。基于PBVS方法的图像平面特征点跟踪轨迹如图5所示，伺服过程历时44 s。

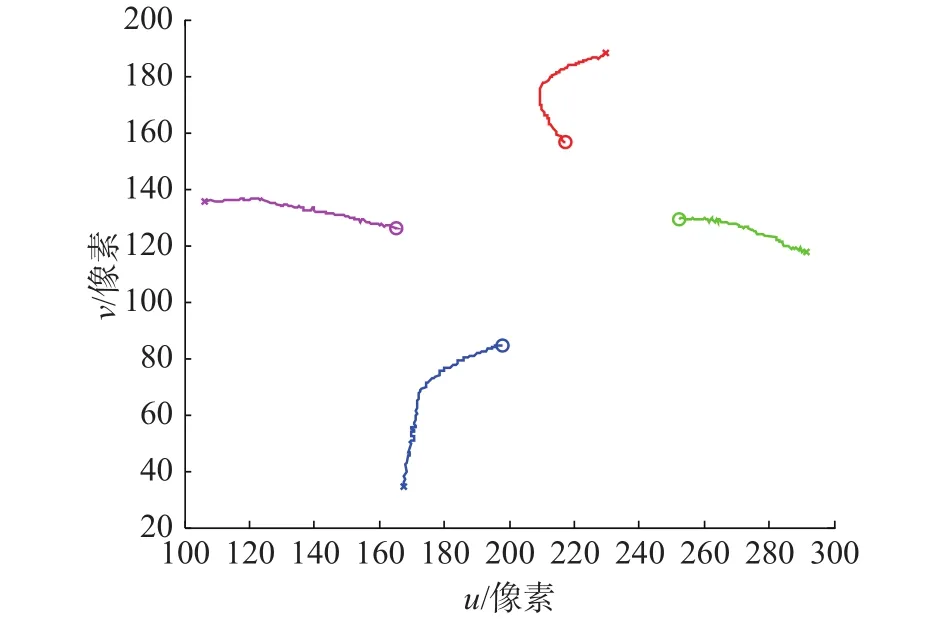
图5 PBVS 图像特征跟踪轨迹，t=44 s

从图5可以看出，PBVS方法的特征点运动轨迹出现了明显的弯曲，图像特征运动轨迹不佳，而且有特征点容易超出摄像机视场范围的问题[8]。

图6所示为基于IBVS方法的图像特征跟踪轨迹，伺服过程历时40 s。虽然图像特征轨迹以近直线方式从初始位置收敛到期望位置，且特征点保持在摄像机视场范围内，但在伺服过程中可以发现，在开始阶段机器人产生较大震动（由于开始阶段图像误差大），机器人运动轨迹不稳定。

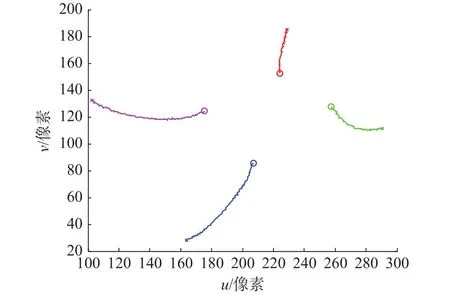
图6 IBVS 图像特征跟踪轨迹，t=40 s

本文算法的图像特征跟踪轨迹如图7所示，伺服过程历时35 s。从图7可以看出，在实际伺服系统中本文算法同样显示了较好的伺服效果，图像特征点以近直线方式从初始位置收敛到期望位置，并且所有特征点没有超出相机的视场范围，在实际伺服过程中机器人运动轨迹稳定，无震动，伺服过程历时最短，效率较高，综合性能较好。

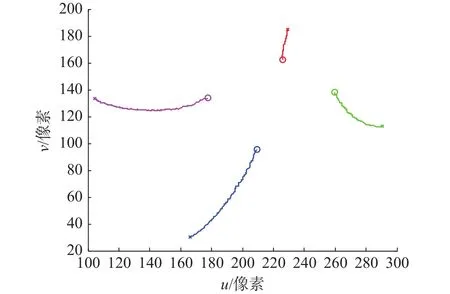
图7 本文算法图像特征跟踪轨迹，t=35 s

6 结束语

针对无标定手眼机器人视觉伺服控制问题，研究了基于图像轨迹规划与时序控制的视觉伺服控制方法，给出了图像平面和任务空间的轨迹规划方法。同时，设计了扩展卡尔曼滤波器估算目标与相机相对位姿，结合相机测量实现了雅可比矩阵的自适应估算。最后在MATLAB环境和7自由度实际机器人系统中对机器人的目标视觉跟踪进行了仿真及实验验证，并与经典PBVS、IBVS方法进行了比较，验证了本文算法的有效性。