一种用于螺旋锥齿轮齿面测量路径优化的改进遗传算法研究
2022-04-19刘明亮阿达依谢尔亚孜旦王永旭
刘明亮,阿达依·谢尔亚孜旦,王永旭
(新疆大学 机械工程学院,乌鲁木齐 830047)
螺旋锥齿轮因具有传动稳定、承载能力强、传动比大、重合度高等优点,已成为飞机、汽车、船舶等的核心基础件之一。螺旋锥齿轮齿面形态极其复杂,属于曲率非均匀分布曲面[1-2],其特殊的齿面结构给检测带来了巨大的难度。传统的螺旋锥齿轮的测量主要采用专用测量设备,如GMC齿轮测量中心等,设备价格昂贵,测量成本过高;三坐标测量机是一种通用测量装置,降低了测量成本[3]。随着对三坐标测量机测量螺旋锥齿轮齿面的不断研究,为了使测量点能够更加精确的反映待测齿面的形状,螺旋锥齿轮齿面测量点的分布逐渐从均匀分布演变为非均匀分布,测量点的数量也在增加。测量路径的选择和优化是三坐标测量机的关键技术之一:测量路径的优化涉及到多个因素,找到最短的测量路径是解决问题的关键。
螺旋锥齿轮齿面可以看作是一种特殊的自由曲面,许多学者在自由曲面的测量路径规划方面进行了研究。纪小刚等[4]讨论了遗传算法在三坐标测量机测量复杂零件中的应用,将路径优化问题抽象为TSP问题,并且通过实验验证了其正确性;高延峰等[5]利用基本遗传算法对曲面测量路径进行规划,证明了遗传算法优化检测路径的有效性,但是没有考虑到算法自身存在的缺陷;李明富等[6]将萤火虫算法进行离散化以适应自由曲面的测量,对测量序列进行了规划,该算法的优点是操作方便实现简单,但是收敛速度慢,运算效率低;陈大伟等[7]利用基本蚁群算法对检查路径进行优化,证明了其优化结果优于禁忌搜索算法和遗传算法,但没有研究蚁群算法初始迭代时间长且容易陷入局部最优解的问题。
将模拟退火算法强大的局部搜索能力与遗传算法强大的全局搜索能力相结合,提出了一种改进的遗传算法。同时优化了编码方式,减少了计算量,提高了收敛速度。结果证明该算法可以在短时间内规划出更优测量路径。
1 测量路径的构成
三坐标测量机是按照事先设定好的坐标对螺旋锥齿轮齿面上每一个点进行测量,为了提高测量精度最常用的方法是提高测量点的数量。在测量点分布坐标确定后,测量路径的规划则决定了测量效率的高低。如果测量路径不正确甚至会发生测头与工件碰撞,导致测量工作无法正常完成。测量路径优化的目的是尽可能减少测量空运行,在不发生碰撞的情况下测头按照最短的路径依次测量每一个测量点且不发生重复,从而大幅提高检测效率。两个点之间的测头移动轨迹如图1所示。
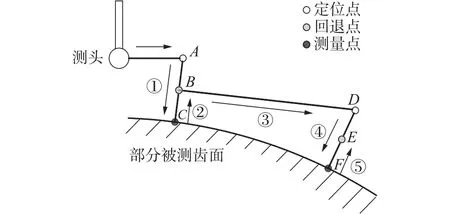
图1 测量路径示意图
从图1可知,测头在测量中有3个过程:到达定位点、接近测量点和退回到回退点。测头先快速到达第一个定位点A,改变角度后从测量点的法向接近测量点,延AC方向以测量速度行进到C点进行测量,测量完成后以回退速度延CB方向快速回退到B点。此时一个测量点测量完成,快速移动到下一个测量点的定位点D点,重复之前的步骤,最终完成所有测量点的测量。测头整个移动路径主要是由①、②、③组成:①段为测头到达定位点后,延测量点法向行进的测量距离:②段为测量完成后测头的回退距离:③段为从当前的回退点到下一个测量点的定位点的距离。测头移动总距离d为

式中:t为全部测量距离①与回退距离②的总和;l为回退点到定位点距离③的总和。
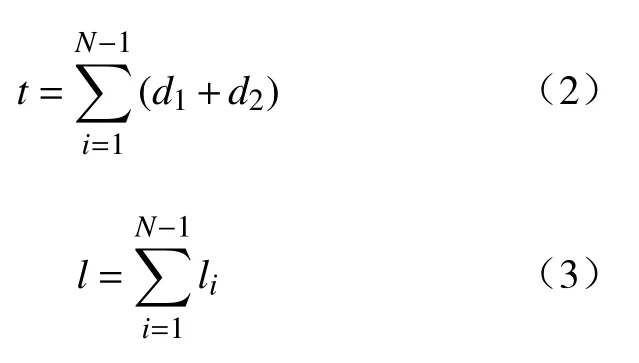
式中:d1为测头从定位点到测量点的距离;d2为测头测量完一个点后的回退距离;N为测量点总数;li为第i个测量点到第i+ 1个测量点的距离,i= 1, 2, 3 , ···,N−1。所以式(1)可以改写成
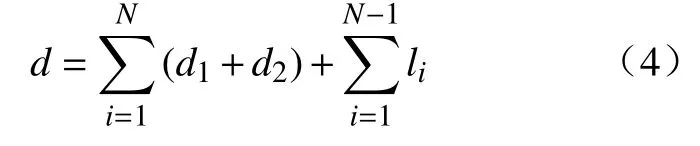
无论测量点如何分布,①、②两段的距离是固定不变的。因此对测量路径的优化可以简化为对③段距离的优化,根据欧式距离方程,测量路径总长l优化的目标函数为:
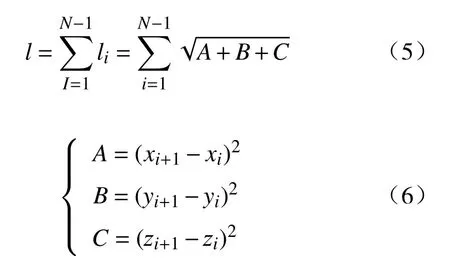
式中:xi、yi、zi为 第i个测量点的坐标值;xi+1、yi+1、zi+1为第i+ 1个测量点的坐标值。优化函数的的最优解为l的极小值。
因此测量路径规划可以理解为:在空间内有每两点距离已知的N个点,测头从某一个点出发并且遍历空间内的每一个点,路径的限制是每个点只能到达一次,最后回到出发点。显然测量点路径优化问题是典型的旅行商问题[6-9]。
2 算法原理、改进及流程
2.1 遗传算法原理
遗传算法是进化算法的一个分支,核心思想来自于达尔文的进化理论。它是模拟自然界生物进化机制发展起来的随机全局搜索和优化方式,具体非常强的全局搜索能力[10]。对问题潜在的解进行编码,每个个体代表遗传算法的一个解决方案,模拟生物进化中的染色体基因的选择、交叉、变异等过程,不断产生新的子代,采用适应度函数模拟自然界的优胜劣汰来判断新解的优劣,直到产生最优解[11]。
2.2 算法改进
算法改进:遗传算法有着非常好的全局搜索能力,但是局部搜索能力不足,经常会陷入局部收敛,也就是“早熟现象”[12]。模拟退火算法来源于固体的物理退火原理,先给定固体一个初始温度,让其按照一定的降温速率衰减,在降温的过程中不断产生新解,并判断选择最优解,直到达到设定的最终温度[13]。模拟退火算法的核心是Metropolis准则[14],主要原理为以一定的概率接受坏解,跳出局部最优的陷阱。因此模拟退火算法非常好的解决了局部收敛的问题,但是却存在着全局搜索能力差及效率不高的问题。综上结合螺旋锥齿轮齿面测量路径优化的实际情况,算法主要在以下方面进行了改进:
1)将模拟退火算法的新解产生规则应用到遗传算法中作为改进遗传算法的进化逆转与退火操作;
2)使用模拟退火算法的Metropolis准则进行判断,在一定程度上接受坏解,完成后进行降温操作;
3)允许子代数量少于父代,重新插入部分父代到子代中补齐新的种群数量,使算法维持较好的多样性;
4)采用坐标编号进行编码,方便交叉与变异,算法收敛效率更高;
5)利用三段法进行染色体交叉,通过建立映射修复了基因冲突;
6)采用了轮盘赌的选择方法,并采用精度较高的随机数指针法。
改进的遗传算法流程如图2所示。
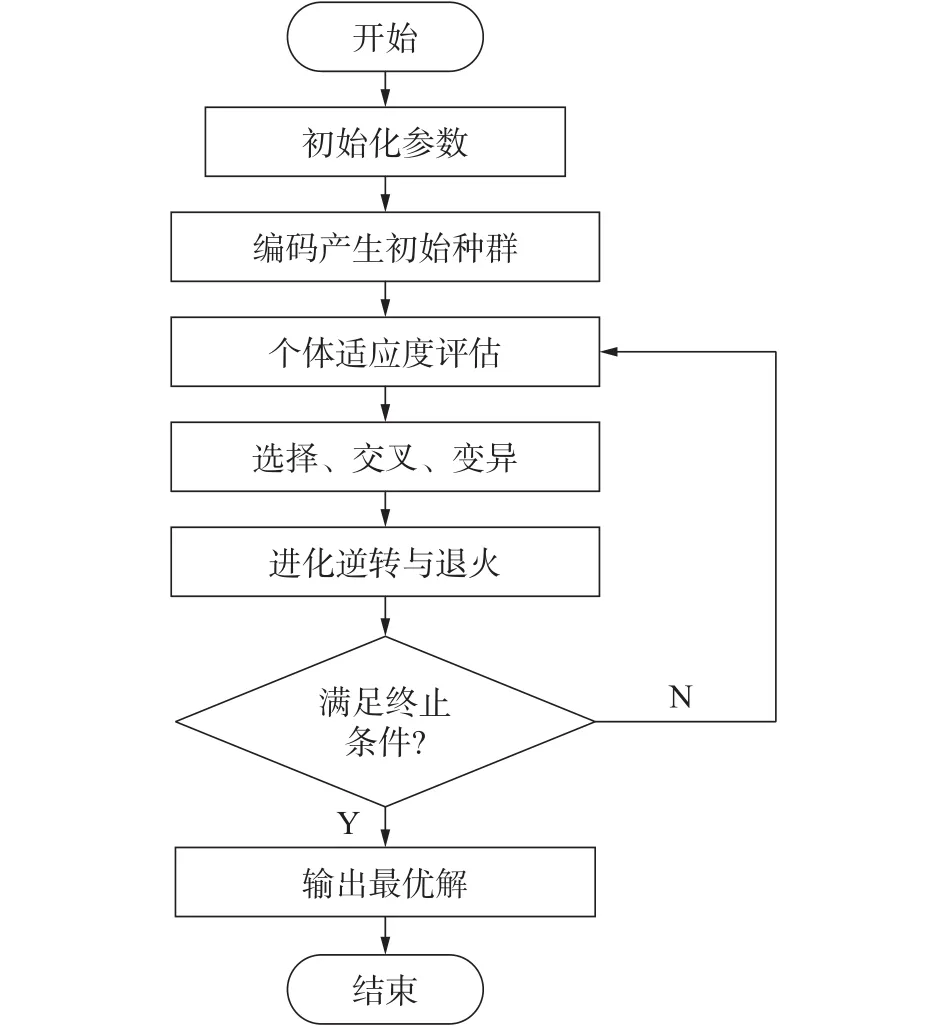
图2 改进的遗传算法流程图
2.3 具体算法流程
步骤1 导入测量点坐标文件,初始化遗传算法各参数设置。种群数量100,交叉概率0.8,变异概率 0.05,代沟 0.9,初始温度 1000 ℃,结束温度0.0001 ℃,降温速率 0.9,最低迭代次数 500。
步骤2 将三坐标测量机测头从起始点到目标点的运行路径作为遗传算法中的一条染色体[15],采用坐标编号进行顺序编码,通过编码的排列组合搜索出最优解,此编码模式非常适用于测量的路径优化问题。确定顺序编码模式后随机产生初始种群,计算路线总长度,得到目标函数初始解。
步骤3 结合目标函数(式(5)),要使l最短,因此适应度函数取路径总长度的倒数,即
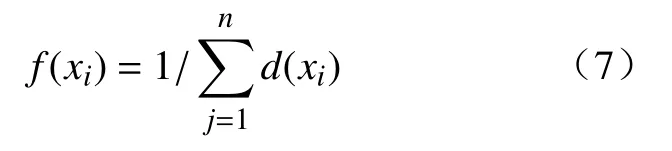
式中d(xi)(i=1,2,3,···,n)为第i段路径的长度。根据适应度函数对个体进行评估,确定每个个体的适应度。
步骤4 使用轮盘赌进行随机选择。适应度越高,扇形面积越大,被选择到的几率也越大。
第i个个体被选中的概率为p(xi),表达式为
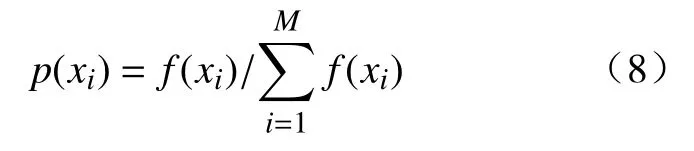
式中:M为个体总数;xi(i=1,2,3,···,M)为第i个个体;f(xi)为第i个个体的适应度。
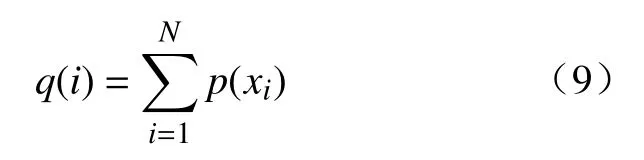
式中qi为计算累计适应度。
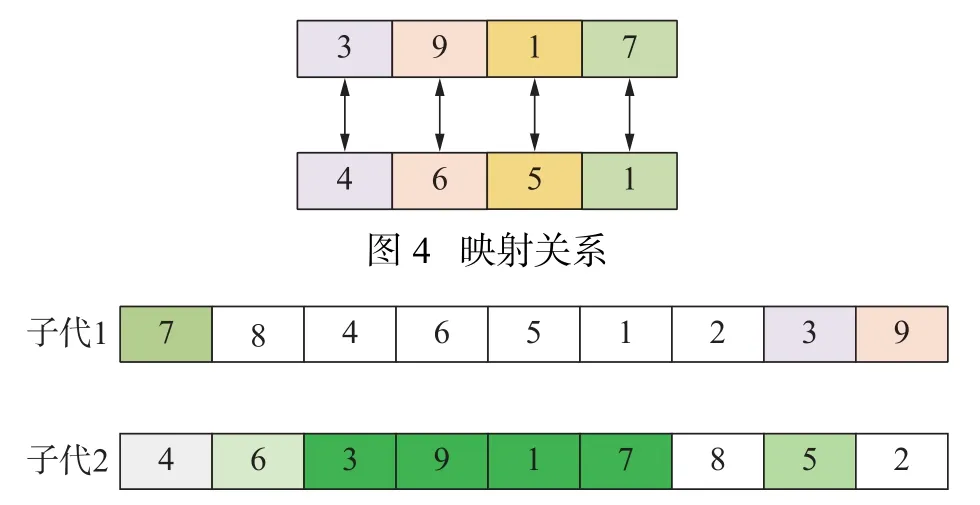
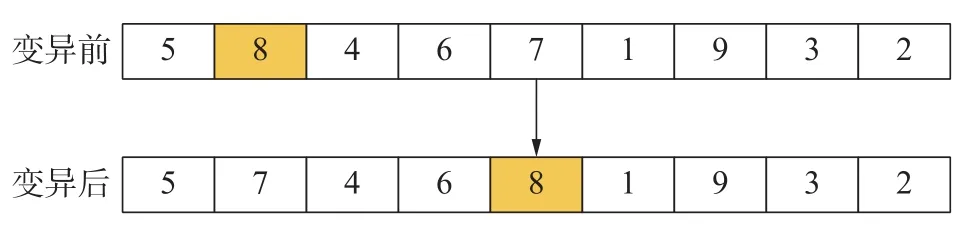
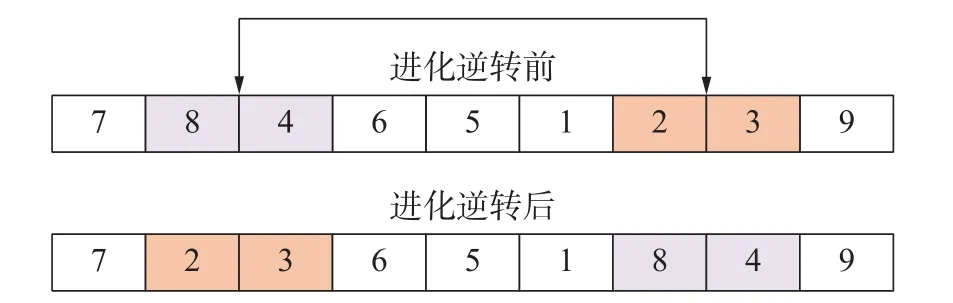
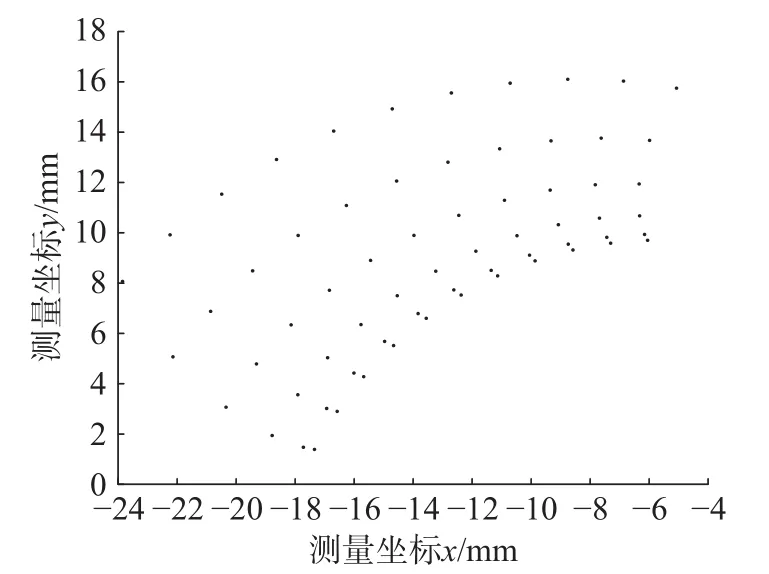
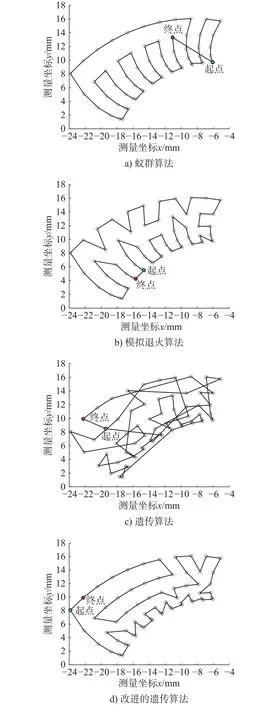
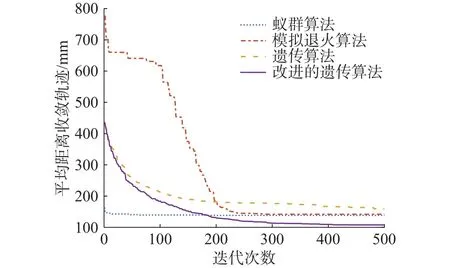
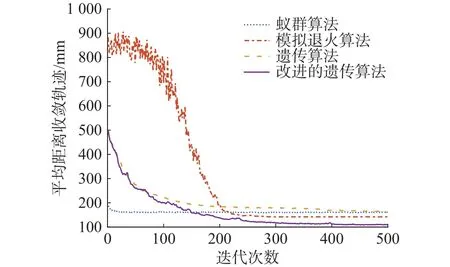
使用rank函数随机生成指针r∈[0,1],若q(1)>r,则个体x1被选择,否则个体xi被选择,且满足q(i) 步骤5 采用部分匹配交叉的方法进行交叉互换。如图3所示,随机选择一对染色体,将每个染色体的基因随机分为三段,要交换的两个染色体分段位置相同,确定交换部分的起止位置,进行交叉互换,产生原始子代个体。 图3 交叉互换 图交叉互换交换完成后检测是否发生冲突,如图4所示根据交换的两组基因建立一个映射关系,若交换后一个染色体中存在两个相同的基因,则根据映射关系转换为没有冲突的基因。如图3所示交换完成后原始子代1中有两个基因5,通过映射关系转换没有参与交换的基因5为基因7。同理,基因6转换为基因9,基因4转换为基因3,以此类推直到没有冲突为止。最终产生的子代如图5所示。 图5 最终子代基因 步骤6 变异操作,对每条染色体产生一个随机数r∈[0,1],若r≤pm则如图6所示任取两个位置交换坐标编号,否则不发生变异。其中pm为变异概率。 图6 变异 步骤7 进化逆转与退火,根据模拟退火算法的原理,需要对当前解扰动产生一个新解,常用的方法有随机交换、翻转、平移等方法。这里采用一个水平翻转的函数,如图7所示随机选取染色体的一部分进行逆序,获得了新的染色体。 图7 进化逆转 利于距离矩阵计算逆序前后结果的大小,使用Metropolis准则接受新解。接受概率为: 式中: Δd为距离的增量, Δd=d(xi+1)−d(xi),xi+1为当前新解,xi为旧解,如果新解的测量距离小于旧解则接受新解,否则按概率p接受新解。随后系统进行降温,表达式为 式中:T为当前温度;T0为初始温度;a为降温速率。 最后从父代中选择一定数量的优秀个体到子代中形成新的种群,进一步提高基因的多样性。 步骤8 返回步骤3,不断进化迭代,直到产生最优解。迭代次数达到500后程序结束,输出最优解。 以按照一定规律分布的非均匀螺旋锥齿轮小轮齿面测量点为例进行仿真试验,总共66个点,测量点分布如图8所示。 图8 测量点分布图 为了比较各类算法的路径优化效果,分别使用蚁群算法[16]、模拟退火算法、遗传算法和改进的遗传算法进行最短路径优化。因为用到的智能算法都具有随机性,为保证结果准确,在同一测试平台和相同的参数设置下各算法连续运行50次,取各自平均值进行统计。优化后测量路径的距离和算法运行时间如表1所示。 表1 仿真结果 得到的路径优化效果如图9所示(挑选各算法50次优化中最优解展示)。 图9 各算法测量路径优化结果 从图9与表1可以清晰的看出:遗传算法的路径最为杂乱,测量路径最长,算法运行时间较短;模拟退火算法的路径相对规整,测量路径优化相对遗传算法提升较大,算法运行时间较长;蚁群算法测量路径更短但是路线存在交叉,明显不是最优解,且由于初始信息素不足导致迭代速度非常慢,算法运行时间最长;改进的遗传算法路径非常规整,测量路径最短且没有发生交叉,算法运行时间也最短;改进的遗传算法测量路径比蚁群算法缩短了22.4%,比模拟退火算法缩短了24.5%,比遗传算法缩短了41.8%;改进的遗传算法较遗传算法运行时间减少了58.9%。 各算法最短收敛轨迹如图10所示。可以看出,蚁群算法的收敛速度最快,在50次迭代前基本达到其最优解,但是显然蚁群算法得到的并不是目标函数的最优解,因此蚁群算法出现了局部最优解的问题;遗传算法初始收敛轨迹与改进的遗传算法一致,因为染色体多样性的不足,也陷入了局部最优解的,最终收敛结果最差;模拟退火算法收敛最慢,经过不断迭代,优化结果与蚁群算法接近;改进的遗传算法收敛速度仅次于蚁群算法,经过迭代进化的最优解远远优于其他算法。 图10 各算法最短收敛轨迹 各算法平均收敛轨迹如图11所示,可以看出模拟退火算法收敛过程中存在明显的震荡,说明其收敛效率较低。改进的遗传算法曲线相对光滑,没有出现明显的震荡,收敛效率高,再一次证明了其在解决优化问题上的优势。 图11 各算法平均收敛轨迹 针对三坐标测量机测量螺旋锥齿轮齿面原理进行了分析,对智能算法的测量路径优化进行了研究。结合模拟退火算法与遗传算法的优缺点与实际测量情况,提出了使用改进的遗传算法解决测量路径优化的问题,通过与其他算法的对比证实了算法的可行性。该方法明显的缩短了测量路径,降低了测量成本,提高了齿面的测量效率,为了螺旋锥齿轮齿面测量路径规划提出了一种有效的优化方案。该路径优化方案也可以用于自由曲面的测量,测量点规模越大越能体现其优势。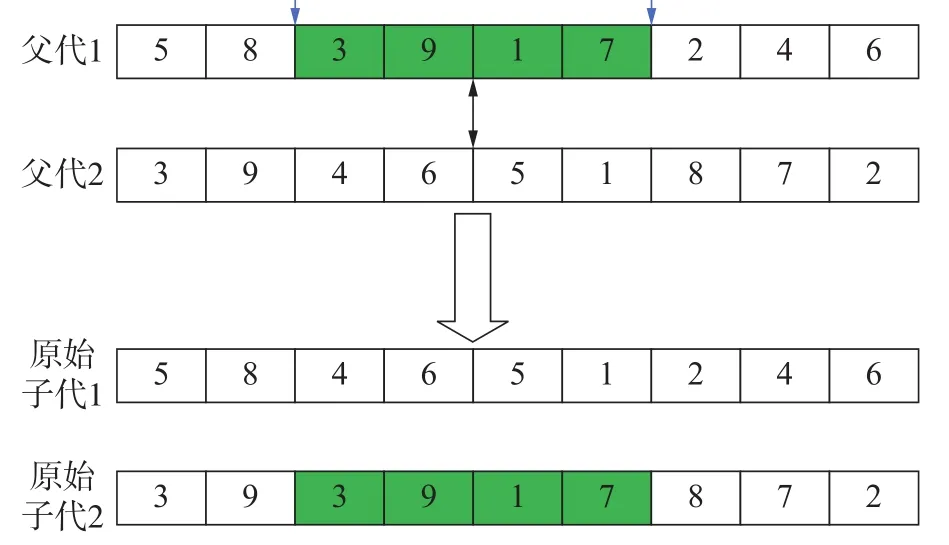
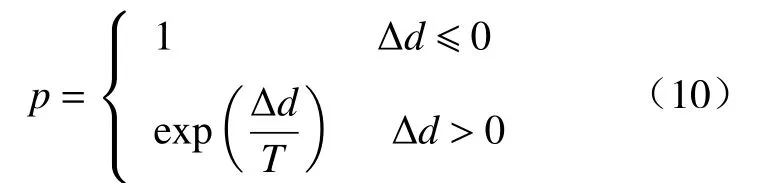

3 仿真试验

4 结论
