求解PageRank问题的重启GMRES修正的多分裂迭代法*

肖文可，陈星玎

（北京工商大学 数学与统计学院，北京 100048）

引 言

Google 搜索引擎以其著名的PageRank 算法成为近年来最成功的搜索引擎之一.Brin 和Page 于1998 年提出了PageRank 算法[1]，该算法通过分析网络的链接结构获得网页的重要程度排名.PageRank 问题就是求解Google 矩阵A的首特征值1 所对应的特征向量，即线性系统的解.Google 矩阵A是矩阵P与矩阵veT的凸组合，即

其中α ∈(0,1)是阻尼因子，e=(1,1,···,1)T，v=e/n，矩阵P是网络的超链接结构[2]所定义的随机矩阵，n为矩阵P的维数.如图1 所示，由4 个网页构成的超链接结构，它所定义的随机矩阵P4，其元素pij表示从网页i链接到网页j的概率，元素值都落在[0,1]之间，且满足每行和为1，

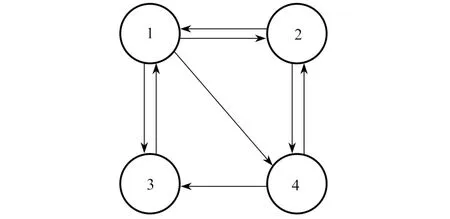
图1 4 个网页的超链接结构Fig.1 The hyperlink structure of 4 pages

Google 矩阵A是 一个高维不可约、非周期的随机矩阵.当 α越接近于1 时，网络矩阵P占比越大，PageRank 问题越接近于真实情况，但越难以求解.

最初求解PageRank 问题(1)的算法是幂法[3].幂法单次迭代计算量小，但收敛速度慢.尤其当阻尼因子α接近1 时，幂法几乎不收敛.随后产生了幂法的加速方法，如二次外推法[2]、修正的幂外推法[4]等.另一方面，利用eTx=1，由式(1)、(2) 可得

那么，特征值问题(1)可以转化为下面线性方程组的求解，即

其中I表示n阶单位矩阵.针对线性方程组(4)，学者们构造了许多迭代方法进行求解，如内外迭代(inner-outer,IO)法[5]、两步分裂迭代法[6]、广义二级分裂迭代法[7]、多步幂法修正的广义二级分裂迭代法[8]和多分裂迭代(MSI)法[9]等.近年来，基于Krylov 子空间的迭代方法由于其特有的优势被广泛用于线性方程组的求解.虽然Krylov 子空间方法的收敛速度快，但是这类方法的单次迭代计算量大，存储空间消耗大，在使用时往往需要与已有的基本迭代法相结合[10-12].本文将Krylov 子空间方法中的重启GMRES 方法[13]与MSI 法相结合，提出了一种重启GMRES 修正的多分裂迭代(GMSI)方法来求解线性方程组(4).

本文的结构如下：第1 节简要介绍了MSI 法和重启GMRES 方法；第2 节给出了重启GMRES 修正的多分裂迭代方法的计算流程；第3 节给出了新方法的收敛性分析；第4 节通过数值实验验证了新方法的有效性；最后进行总结.

1 MSI 法和重启GMRES 方法

本节中，我们将简要回顾MSI 法和重启GMRES 方法.

1.1 MSI 法

Gu 等[9]在线性方程组(4)中引入两个参数 β1和 β2，提出了一种基于多分裂的两步迭代法，即MSI 法.

MSI 方法 给定初始向量x(0)，对k=0,1,2,···，计算如下迭代：

直至{x(k)}收敛.其中参数 βi满足0 ≤βi＜α(i=1,2)，，即对每一步迭代解进行归一化.

我们采用IO 法求解线性系统(5).定义如下两个内线性系统：

其中

f1=(α-β1)Px(k)+(1-α)v,

f2=(α-β2)Px(k+1/2)+(1-α)v.

然后，采用Richardson 迭代：

计算线性系统(5)中的x(k+1/2)和x(k+1)，注意y(1

l1)=x(k+1/2)，y(2l2)=x(k+1).

MSI 方法的终止标准如下：假设η和τ分别代表内、外迭代终止指标，当

时，内迭代(8)终止；当

时，外迭代(4)终止.

1.2 重启GMRES 方法

Saad 等[13]提出的GMRES 方法被广泛应用于线性方程组的求解.由于GMRES 方法的时间复杂度和空间复杂度都较大，在实际计算中往往采用重启GMRES 方法[13]，即GMRES(m)，m代表重启数.重启GMRES 方法的具体计算步骤将由算法1 给出.

算法1GMRES(m)方法

步1 开始.给定重启数m，初始向量x0，迭代终止指标τ，计算

r0=(1-α)v-(I-αP)x0, β=‖r0‖2,v1=r0/β.

步2 迭代.对j=1,2,···,m,

步3 计算近似解.xm=x0+Vmym，其中正交基矩阵Vm={vj}1≤j≤m，向量ym是最小二乘问题miny∈Rm‖βe1-y‖2的解，e1=(1,0,···,0)T，={hi j}1≤i≤m+1,1≤j≤m.

步4 重启.计算rm=(1-α)v-(I-αP)xm，若‖rm‖2＜τ，则算法停止；否则x0←xm，v1=rm/‖rm‖2转至步2.

2 重启GMRES-MSI 方法

本文把重启GMRES 方法与MSI 法相结合，提出了一种求解PageRank 问题(4)的新方法，即重启GMRES 修正的多分裂迭代法，简记为GMRES(m)-MSI 方法.该方法的基本思想是：给定一个初始向量x0，首先利用GMRES(m)方法计算一个近似解x1，如果x1未达到收敛精度，那么将x1作为MSI 方法的初始向量继续求解.重复上述过程，直至达到收敛精度.算法流程如图2 所示.

图2 重启GMRES-MSI 方法的计算流程图Fig.2 The calculation flow chart for the restarted GMRES-MSI method

在GMRES(m)-MSI 方法中，用于控制GMRES(m)方法和MSI 方法之间转换的三个参数分别记为 α1，ν和ϖ.ν表示MSI 方法的当前迭代次数，ϖ表示MSI 方法的最大迭代次数.由于Google 矩阵的第二特征值的模小于等于α[14]，所以 α1的选择应该小于α，取α1=α-0.1.设rpre与rcur分别表示前后两步MSI 方法的残差范数，定义ζ=rcur/rpre，通过比较ζ和 α1的大小来决定是否执行ν=ν+1.若ν ＞ϖ，则终止MSI 方法，进入GMRES(m)方法；否则，继续运行MSI 方法.具体计算步骤见算法2.

算法2GMRES(m)-MSI 方法

步1 开始.选取初始向量x0，重启数m，内、外迭代终止指标分别为η和τ，参数 β1，β2和 ϖ，初始误差取r=1.

步2 运行GMRES(m)方法2 至3 次，若得到的近似解达到收敛精度，算法停止，否则继续.

步3 将GMRES(m)方法得到的近似解x1作为MSI 方法的初始向量.

算法停止，否则转向步2.

3 算法的收敛性分析

引理1设x(k)是MSI 方法的第k步迭代解，那么第k+1步迭代解为x(k+1)=Gx(k)，迭代矩阵

G=(I-β2P)-1[(α-β2)P(I-β1P)-1(A-β1P)+(1-α)veT].

证明因为0 ≤β ＜α ＜1且P是随机矩阵，所以I-βiP(i=1,2)是严格对角占优矩阵，因此I-βiP(i=1,2)是可逆矩阵.

由于在MSI 方法中采用了归一化处理，每一步的迭代解满足eTx(k)=1，那么由式(5)可得

因此，迭代矩阵G为

G=(I-β2P)-1[(α-β2)P(I-β1P)-1(A-β1P)+(1-α)veT].□

将GMRES(m)方法计算的近似解x1作为MSI 方法的初始向量，由引理1 得，经过l次MSI 方法，求得近似解x*1为

x*1=Glx1,l≥ϖ.

然后，将x*1作为GMRES(m)方法的初始向量构造新的Krylov 子空间Km，即

Km=span{v*1,(I-αP)v*1,···,(I-αP)m-1v*1},

其中

v*1=r*0/‖r*0‖2,r*0=(1-α)v-(I-αP)x*1.

设Pm是最高次数不超过m次的全体多项式的集合，不失一般性，假设矩阵A的特征值按照降序排列为[15]

1=|λ1|＞|λ2|≥··· ≥|λn-1|≥|λn|.

引理2[13]设I-αP可对角化，且(I-αP)=XΛX-1，这里Λ=diag(s1,s2,···,sn)，si(i=1,2,···,n)是矩阵I-αP的特征值，定义

那么采用GMRES(m)方法后的残差rm满足不等式

‖rm‖2≤κ2(X)ε(m)‖r0‖2,

其中

κ2(X)=‖X‖2‖X-1‖2.

引理3[15]设随机矩阵P的特征值为{1,π2,···,πn}，则Google 矩阵A的特征值为{1,απ2,···,απn}.

引理4设随机矩阵P的特征值为{1,π2,···,πn}，则矩阵

A-β1P=(α-β1)P+(1-α)veT

的特征值分别为1-β1和(α-β1)πi(i=2,3,···,n).

证明由于P是随机矩阵，所以(1,e)为P的特征对.设Q=(e,L)是一个非奇异矩阵，Q的第一列为矩阵P的特征向量e.设那么

则有yTe=1，YTe=0.因此，

因此，YTPL有特征值π2,π3,···,πn(文献[15]中，定理5.1).对矩阵A-β1P做相似变换，得

因此，矩阵A-β1P的特征值为1-β1和(α-β1)πi(i=2,3,···,n).□

下面，我们给出GMRES(m)-MSI 方法的收敛性分析.

定理1设I-αP可对角化[16]，则采用GMRES(m)-MSI 方法后的残差rm满足不等式

证明由于I-αP可对角化，根据引理2 有

‖rm‖2≤κ2(X)ε(m)‖r*0‖2.

由引理3 可知，Google 矩阵A的特征值λi=απi(i=2,3,···,n)，矩阵(I-βjP)-1(j=1,2)的特征值为(i=1,2,···,n).由引理4 可知，矩阵A-β1P的特征值为λi-β1πi(i=1,2,···,n).

根据引理4 的证明，有

(1-α)veTd1=1-αdi=0(i=2,3,···,n)

那么矩阵的特征值为和.

由d1=1-α,π1=1,λ1=1，得ϕ1=1.

对于i=2,3,···,n，有

又因为|πi|≤1(i=2,3,···,n)，有|λi|≤α(i=2,3,···,n)，从而

假设由GMRES(m)方法计算得到的近似解x1可以表示为其中 γi不全为零，µi(i=1,2,···,n)是矩阵A的一组特征基，且‖µi‖2=1.

由于

及Gµ1=µ1，Glµ1=µ1，有

4 数值实验

本节我们将通过数值实验验证GMRES(m)-MSI 方法的有效性.所有的数值实验都是在内存8 GB，主频2.6 GHZ，操作系统Windows 10，处理器为Intel(R) Core(TM)i5-4210M 的计算机上用MATLAB(2019a)完成的.

我们选取3 个网络矩阵进行数值实验，分别为zkyG 矩阵、Email-Enron 矩阵和web-Stanford 矩阵.zkyG 矩阵记录了2014 年2 月与中国科学院主页http://www.cas.cn 相关的5 000 个网站的邻接矩阵，Email-Enron 矩阵记录了2003 年与美国安然公司有电子邮件来往的36 692 个邮件所构成的邻接矩阵，web-Stanford 矩阵记录了2002 年与斯坦福大学主页https://www.stanford.edu 相关的281 903 个网站的邻接矩阵.以上网络矩阵都可以从https://sparse.tamu.edu 上获得，它们的性质见表1.表中dimension 代表矩阵的维数，nonzeros 代表矩阵的非零元个数，average nonzeros 代表矩阵平均每行非零元的个数.

表1 网络矩阵的性质Table 1 The nature of the network matrix

当阻尼因子α取不同的值时，我们分别比较了内外迭代IO 方法、MSI 方法和GMRES(m)-MSI 方法(GMSI)的计算效果.在IO 方法中，选取β=0.5，η=10-2.为了保证数值实验的公平，在MSI 方法和GMRES(m)-MSI 方法中同样取η=10-2.另外，根据经验取值，在MSI 方法中分别取β1=0.5,β2=0.85(zkyG 矩阵、web-Stanford 矩阵)，以及β1=β2=0.5(Email-Enron 矩阵)，算法会有较好的表现.在GMRES(m)-MSI 方法中，选取同样的 β1和β2，重启数m=8，ϖ=10.在这三种方法中，选取的初始向量x0=e/n，迭代终止指标τ=10-8.

为了测试GMRES(m)-MSI 方法的加速效果，我们定义相对加速比

其中TMSI代表MSI 方法的运行时间，TGMSI代表GMRES(m)-MSI 方法的运行时间.

表2～4 分别给出了 α取不同值时，这3 种方法在不同测试矩阵上的迭代步数N和CPU 计算时间T（以秒为单位）.从数值结果可见：GMRES(m)-MSI 方法优于MSI 方法和IO 方法，并且随着 α的不断增大，GMRES(m)-MSI 方法的加速效果越来越明显.

表2 ZkyG 矩阵Table 2 The zkyG matrix

表3 Email-Enron 矩阵Table 3 The Email-Enron matrix

表4 Web-Stanford 矩阵Table 4 The web-Stanford matrix

图3～5 分别给出了α取不同值时，3 种方法计算不同测试矩阵的收敛曲线.横轴N代表迭代步数，纵轴r代表残差范数，即r=‖αz+(1-α)v-x‖2.可以清楚看到，GMRES(m)-MSI 方法的收敛速度是最快的.

图3 α取不同值时, 3 种方法计算zkyG 矩阵的收敛曲线图Fig.3 For different α values, the convergence curves of the zkyG matrix with the 3 methods

图4 α取不同值时, 3 种方法计算Email-Enron 矩阵的收敛曲线图Fig.4 For different α values, the convergence curves of the Email-Enron matrix with the 3 methods

图5 α取不同值时, 3 种方法计算web-Stanford 矩阵的收敛曲线图Fig.5 For different α values, the convergence curves of the web-Stanford matrix with the 3 methods

5 总 结

本文给出了一种求解PageRank 问题的新方法，即重启GMRES 方法修正的多分裂迭代法，GMRES(m)-MSI 方法.我们不仅给出了GMRES(m)-MSI 方法的收敛性证明，而且通过数值实验验证了新方法的有效性.数值结果表明，当阻尼因子α接近于1 时，GMRES(m)-MSI 方法的收敛速度远远优于IO 法和MSI 法.下一步，我们将从理论上研究GMRES(m)-MSI 方法中最优参数的选取原则.