兼具科教融合理念与计算思维培养的教学改革

2022-04-19杨松高亚男王雪李凡

高教学刊 2022年9期

杨松高亚男王雪李凡

摘要：文章以算法与算法复杂性理论课程为例，探讨科教融合视域下，培养学生新型计算思维的课程教学改革。文中综合分析计算机类课程当前教学中的不足，针对分析结果重新定义教学改革的目标。在此基础上，文章分别从授课主体和学习主体的角度出发，从教学内容、教学方式、教学成果产出、课程考核和课程评价反馈五个方面出发，提出融合科学研究、计算思维培养的，具有多元性、协同交叉性的教学改革举措。通过文章提出的算法与算法复杂性理论课程的教学改革举措，以期提高课程教学时间利用率，为培养具备新型计算思维并兼具科研特性的计算机人才提供有力保障。

关键词：科教融合;计算思维;算法与算法复杂性理论;教学目标;教学方法;教学评价

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2022）09-0089-06

Abstract： Taking an example of Algorithms and Algorithm Complexity Theory， this article， from the view of the integration of research and education and computational thinking， explores and analyzes the weaknesses of this curriculum teaching. It redefines the objectives of this curriculum reform and proposes reform measures of five aspects： including curriculum content， teaching methods， teaching outputs， teaching examination， and teaching assessment， which improves the teaching efficiency， and provides a strong guarantee for cultivating excellent students with novel computational Thinking and Research Interest.

Keywords： integration of research and education; computational thinking; Algorithms and Algorithm Complexity Theory; teaching targets; teaching methods; teaching assessment

科教融合是世界一流大学的核心办学理念，是我国高等教育强国建设的必然选择[1-2]。不同于科研成果向生產力的转化，科教融合强调科研成果向人才培养资源的转化，其本身是一个知识传授教学的过程。推动科教融合，有利于推动教师打破原先的教学方法，直接培养学生的实践能力、创新能力、解决问题能力，从根本上解决高校课堂教学内容无法适应高速的社会变革的情况，真正实现科研融入教学，教学推动科研的目标[3]。近年来，AI赋能下的云计算、大数据、物联网以及移动计算等新一代信息通信技术的高速发展为各行各业带来了巨大的产业革新和广阔的应用前景。计算机领域中，培养计算思维也由单纯地利用基础概念建立计算模型的过程，转变为依据原始学科领域特点，建立定制化计算模型，来解决各领域特定问题的过程，被称为计算思维2.0[4]。新型计算思维旨在培养学生具备能够适配未来的思维模式，即能够灵活解决人类在未来社会中遇到的问题，而不是像计算机一样机械运转。科教融合理念指导下，培养学生的新型计算思维，是计算机专业适应新一代信息技术发展和产业革新、推进高校人才培养模式转型、培养引领社会发展创新型人才的必然要求和必经之路。其对计算机专业相关课程的教学实践和人才培养提出了新要求。

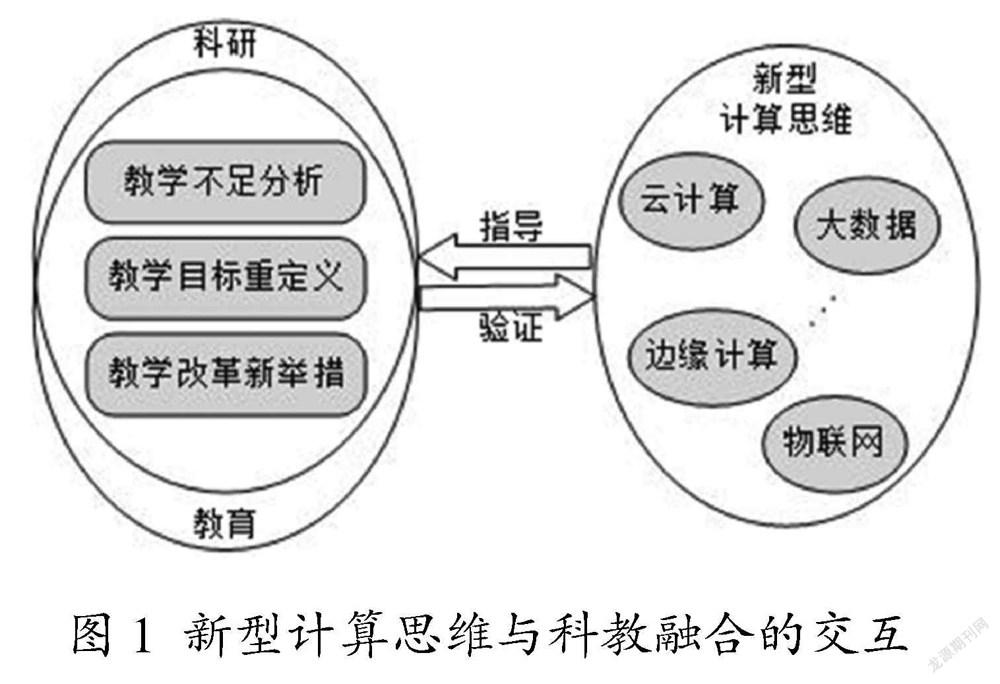
算法与算法复杂性理论是计算机相关专业中研究生培养过程中的核心课程，也是面向问题建模、多门计算机专业基础课、数学理论课的关键衔接[5]。该课程旨在向学生教授计算机经典算法和现代算法的方法原理、设计和复杂度分析，增强学生算法理论基础和算法设计思维，并借助数据结构解决实际应用中或科学研究中的非数值型计算问题[6]。本门课程对培养计算机专业学生的实践能力，培养算法思维，形成职业技术支撑具有重要意义。如图1所示，以该课程为例，以培养具备新型计算思维人才为指导改革和验证改革效果的工具，从科教融合角度出发，分析算法与算法复杂性理论课程教学中存在的不足、重新定义其课程目标并提出课程改革新举措。

图1 新型计算思维与科教融合的交互

一、教学过程中存在的问题及其分析

（一）科研“零”参与的知识传授

传统的算法与算法复杂性理论课程主要涵盖的内容有NP理论、图论算法以及各类经典算法的算法设计原理和算法复杂性分析，涉及常用数学工具、初级数据结构、计算理论等先修基础知识储备。教师虽投入地讲述系统性知识，但学生则只能通过“听记”“看记”“偶尔答”的参与方式“被动”地接收，前沿科学研究和新技术的缺乏、陈旧且难以理解的课程内容极难激发学生的学习兴趣，造成学生缺乏学习的独立性、主动性和探索性，进而形成“背诵”算法而不是“理解”算法的思维惯性。

（二）课程学习与导师科研任务的差异性

在整个研究生学习过程中，课程学习只占学习时间花费的极小比例。大多数研究生以导师的科研项目和完成毕设论文为主要任务。课堂上的大部分学生不会完全沉浸思考并享受学习算法分析与设计的乐趣，而是以结课后获取“学分”或“高分”为目的。这种目标导向的差异性导致学生在课程上的投入与其自身的主要任务之间无法同频共振，甚至存在时间利用上的冲突。

（三）“高聚合式”的课程内容设置

课程模块间较低的内容相关性导致了独立的、单元式的、低耦合的教学课时分配。这使得每个模块学习结束后，学生难以对整体教学内容前后联系而产生断层式的知识遗忘。尤其“传统”算法与“现代”算法（强化学习、区块链、图神经网络等）的模块独立，让学生无法从中体会算法之间的共通性和差异性，无法理解不同算法在解决同一个问题时的内在联系和有机统一。而先前学习的知识往往在结课后的考核复习中才被重新拾起学习。这种“一终一考”式的学习方法，不利于学生系统化学习和全局掌握课程内容，更无法做到温故知新和灵活运用。

（四）教师的科教“矛盾”

科研驱动式的高校建设指标，使得教师在时间和精力有限的前提下，必须投入更多的科研精力以保证科研指标完成。陈旧的课程内容无法匹配教师重点关注的前沿科研动态。教师的科研投入和教学投入之间同时存在此消彼长的“矛盾”现象[7]。此外，机械式教学方法使教师的教学主动性与学生的学习参与性之间产生负向相抵消的循环依存关系。

（五）高等教育与社会发展“脱节”

大学作为从事知识研究的机构，其学术性及相对独立性应为引领社会发展提供现实可能，应培养能引领社会发展的人才[8]。然而近年，学校教授的陈旧知识已不能适应社会的飞速发展，导致众多开创性的技术、产品、学科融合理念大多出自企事业单位，由单位内研究团队设计产生，反过来反哺学校，出现了企业带动大学发展、引领社会进步的社会性现象，违背了大学建立的初衷。

二、课程改革目标

在科教融合理念指导下，以培养学生新型计算思维为目的驱动，以算法与算法复杂性理论课程为例，结合上述对目前课程教学过程中存在不足的分析，本文提出“双度双念”的课程教学改革目标。

（一）教学科研关联度

教學应融合不同科研应用场景，借助同一算法理论从不同角度解决多个方向的科研问题，将传统单一维度的算法教学转变为高维度、多方位、横向融合、纵向深入的综合性教学，实现教学与科研有机统一，将新知识、新思想引入到传统课程教学过程中来，依托前沿科研，为培养新型计算思维的科研人才提供快速成长的捷径，并形成“教师讲授-师生研讨-学生探究”的研究性教学模式。

（二）计算思维多维度

从逻辑思维、实证思维、融合思维等多方面思维角度出发，定义计算机人才培养的新型计算思维。将课程教学或课程学习与计算思维培养方式相结合，采取能够使学生新型思维形成过程更深刻、思维培养方式更具体、形成的计算思维适应性更强的教学举措，并产出内容创新、形式多样的教学成果，提升学生课程学习的成就感和满足感，提高学生的课程参与度和教师讲课的积极主动性。

（三）“多元性”理念

教学的多元性体现于教学过程的方方面面。该理念主张教学过程的多样性、灵活性和应变性，要求教学主体和学习主体在不同的教学阶段中，具备自主选择能力、自主驱动能力、自主评价能力和自主规划能力，进一步提高课堂教学效率，进而激发和培养学生终身学习的能力，实现教师课程教学的灵活适应和学生课程学习效益的长期价值反馈。

（四）“协同交叉性”理念

该理念旨在通过科研与教学、计算思维培养与教学、科研与计算思维培养的两两双向融合，针对课程教学的不同阶段，实现三者的“协同交叉”，循序渐进地激发学习主体的科研能力培养、计算思维培养和教学主体的参与积极性。该理念要求教学过程的不同阶段能相互融合，实现内容维度和时间维度协同创新的双向教学模式。

三、课程改革举措

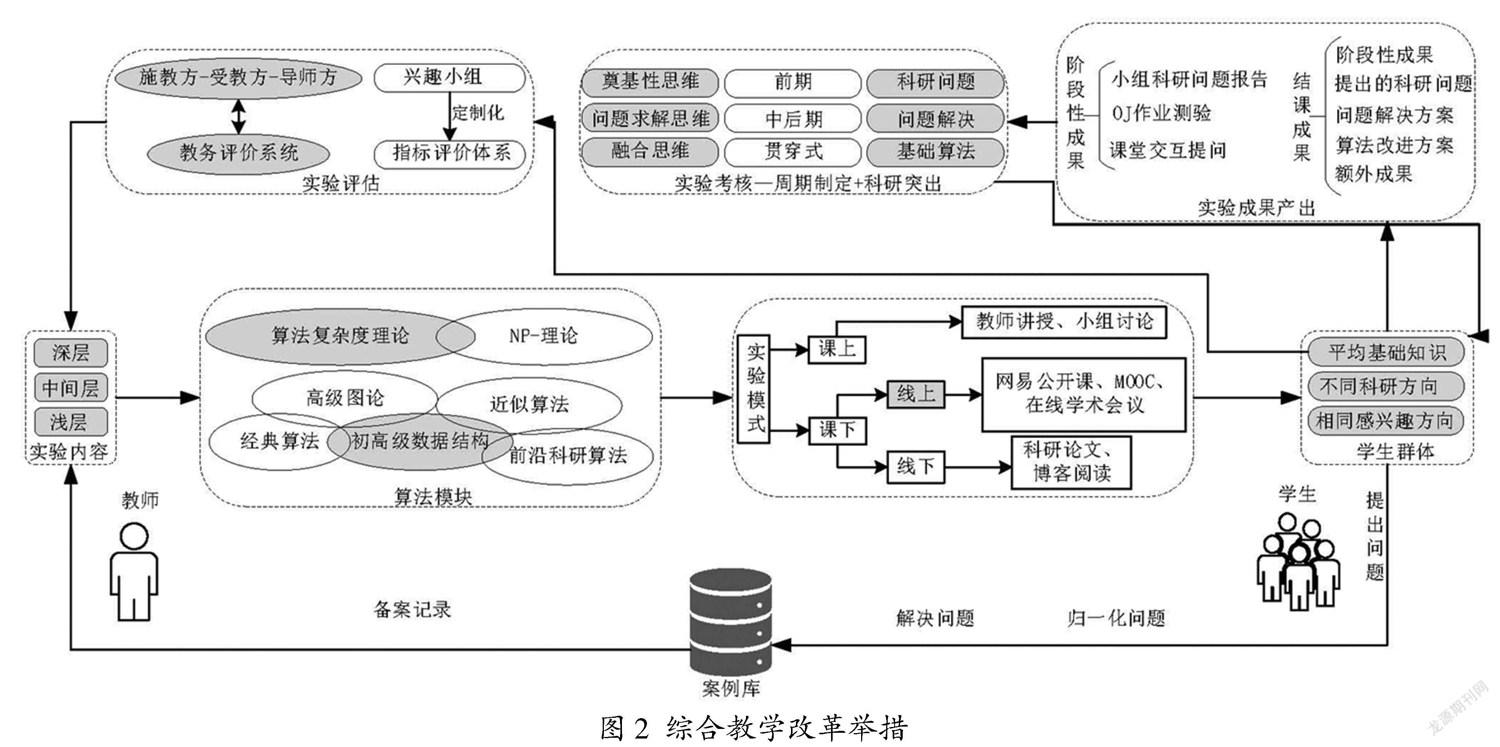
以算法与算法复杂性理论为例，本文探讨了科教融合视域下，培养具备新型计算思维的计算机专业人才的课程教学改革举措。文章分别从教学主体和学习主体出发，从“教学内容、教学方式、教学成果产出、课程考核和教学过程评价”五个方面，以体现教学科研关联度、思维培养方式多维度、教学“多元性”和教学过程的“协同交叉”理念为目标，提出如图2所示的综合教学改革举措。

由“课程内容”出发，使用内容的层次化设置构建算法模块间的内容和课时关联。学生根据课上讲述内容，调整“学习模式”，使用线上、线下方式辅助课程学习。层次化分组后的学生群体，一方面通过“提出问题-归一化问题-解决问题”重塑算法案例库。案例库被“备案记录”用于更新课程内容设置。同时，依据制订的“成果产出”，不同小组针对各自的感兴趣算法模块，完成“阶段性”科研问题报告、问题解决方案、算法改进方案等课程成果产出。“思维导向+科研突出”的课程考核方法，被用于考核产出成果，并将得到的考核成绩反馈给“学生主体”。“学生主体”在得到成绩后，登录“教务评价系统”，根据“定制模块化”的指标评价体系，对课程学习过程进行指标评价，进而反馈给课程内容，用于课程的内容更新。

这种“多元性”“协同交叉性”的综合改革机制，在算法与算法复杂性理论的课程教学过程中，贯彻落实了科教融合理念，考虑了培养新型计算思维人才的教学改革措施。从课程内容的关联性、学生主体的差异性两方面入手，融合科研教育和新型计算思维培养，本文调整了学生学习模式、课程成果产出、课程考核以及课程评价四个方面的规则设置，充分体现了该课程教学的前沿性、创新性、连贯性、自适应性、多元性和协同交叉性。

（一）教学内容

教学内容的改革措施依托于教学主体，主要包括课程内容的层次化设置和基于课程内容构建的教学案例库的实时重塑。

1. 课程内容的层次化设置。根据课程内容辅助理解整体课程内容的重要程度和各模块内容的相关性，将算法与算法复杂性理论的课程内容分为“浅层”“中间层”和“深层”，见表1。

其中，“深层”表示该课程的核心内容和算法设计思想的源头，需占据大多数课时且实行贯穿式教学，对全局内容理解起关键作用。“中间层”表示随着数据规模增大能权衡算法时空复杂度和结果准确率的算法内容。该层的内容应被详细教授、讨论，让学生充分掌握算法原理。“浅层”则表示已在本科阶段学习过的、无法适应新型计算思维培养的传统经典算法内容。“浅层”内容能让学生在快速理解内容的同时，思考与“中间层”算法的联系，对算法的演进过程产生新的认识。

这种伴随贯穿式的、由复杂到简单的层次化内容设置能让学生更易从全局角度理解不同模块间算法内容的相关性，对比分析经典算法与现代算法间的优劣性，且通过深层核心内容的不断反复学习，进而产生交互启发式科研兴趣。

2. 重塑案例化教学。从学生接收知识的角度看，案例库的使用大多遵循教师讲授、算法理解和学生动手实现三个阶段。而传统的案例，如背包问题、棋盘覆盖问题、蓄水池问题等，大多取材于分治、减治、排序等经典算法问题。问题约简严重，解决方案固定，无法与前沿科研问题建立直接相关关系，是该课程内容不能被创新应用于科研推动的主要原因。科研转化型实验具有综合性强、精准度高的特点，且在教学过程中，可以采取多种途径来达到科研知识传授的教学目标[9]。

课程应将传统被动式的解决问题转化分解为“提出问题-归一化问题-解决问题”的过程。比拟经典案例算法用于解决现实生活中遇到问题的设计理念，学生根据各自的研究方向或工作涉及的方向，提出相应的科研问题或找工作过程中涉及的企业相关的有趣应用问题，来扩充案例库。如A同学在面试百度时，对面试官问到的大数据量下关键词检索的问题，可进行相应算法约简，构建一个涉及“Hash散列表”和“排序算法”相结合的实用性算法问题;B同学的研究方向为虚拟化网络服务调度，则可将该问题建模为具有网络知识背景的“0-1”背包或多元背包问题，再融入到算法案例库中。进而实现对经典算法问题、科研问题、工业界问题的算法归一化和并行建模分析。

（二）教学方式

从学习主体出发，教学方式的改革举措包括学习主体的个体基础层次化设置和学习主体的混合型学习模式设置。

1. 个体基础层次化设置。美国心理学家桑代克充分肯定了“成人对学习的兴趣并不弱于儿童和青年”且“年龄对学习速率的影响近乎为零”[10]。学生水平参差不齐是影响研究生课程教学效果的重要問题。以兴趣为引导的学生自主选择式的教学过程，更能发挥课程教学的价值。

学习主体的层次化设置分为两步：（1）在课程初期，依据课程设计简单考核问卷。问卷内容包括：经典算法内容的基础知识、研究方向、感兴趣的内容。（2）根据问卷答题结果，对授课群体进行层级划分，将全体学生按“学习基础平均、研究方向不同、感兴趣内容一致”的分配准则划分小组。经典算法内容的基础考核能让教师全面把握学生整体基础知识的掌握程度，在后续课程教学中实现有的放矢的内容教授;相同的“感兴趣内容”统一了组内学生间算法深度的共同探索需求;研究方向的差异性能帮助提出不同的前沿性科研场景问题，扩展组内学生算法学习的宽度;基础知识、学习能力层级的平均化能帮助均衡组间课程内容理解的进度控制。由组内不同层次学生的启发式带动，各小组能完成高效率的算法理解和方法创新。

2. 混合型学习模式。混合型学习模式对培养学生计算思维和应对学生基础的参差不齐具有重要意义[11]。混合型学习模式按时间划分为课上学习和课下学习两个学习区间。

课上学习以教师教授、教师学生互动和学生小组间讨论为主。受有限课时的影响，课上学习时间区间短、个体参与度较低。但交互式学习方式的学习效率高，对课程内容的掌握程度较好。

课下学习的途径则丰富多样，可分为线上和线下两种模式。线上学习内容包括课程内容重复学习、课程案例自主搜索和学术会议观看。学生可以通过网易公开课或MOOC平台中的MIT、斯坦福、清华大学、国科大等的算法在线开放课程教学视频，进行课程内容的重复学习和查漏补缺。课程经典案例的巩固学习则可以通过各高校或科研机构、互联网企业等公开的在线测试平台，如北京大学OJ、力扣等。学术会议则可通过各学术会议官网、腾讯在线会议等方式进行观看。学生课下的线下模式学习，主要根据各自的科研方向进行课程内容的选择性学习。

（三）教学成果产出

OBE（Outcome-based Education）教育模式强调“成果产出”能检测、激励学生的课程学习并辅助修正教师的教学方法和教学进度[12]。阶段性成果产出能满足学生的短期心理需求，为下一阶段的课程学习产生内在动力[13]。学生及时的阶段性思考和反思也能促进后期的知识接收效果和学习效率[14]。

1. 阶段性成果产出。阶段性成果产出包括：课堂教师交互式提问情况和OJ测验题目;各同学依据科研方向提出的针对该模块算法的科研问题、模块对应算法用于解决所提出科研问题的描述过程。其中，依据“科研成果”转化来的案例，问题模型更复杂，但更具有前沿性和探索性，与导师布置的科研任务相关，能快速激发学生的科研探索欲并同时推进导师科研项目进展，做到“一产两用”。

2. 结课成果产出。结课成果内容主要包括：依据小组的感兴趣算法，各小组成员按照科研方向所建立的案例解决方案、全体同学OJ案例作业提交方案和课堂交互式提问、各小组成员根据自身科研问题作出的解决方案和算法改进方案（小论文或报告）、最终的大作业基础知识考核及额外成果（科研成果转化的报告、专利、论文等）。每届学生所产出的科研成果案例可用于扩展案例库。随着不同方向科研进展的不断推进，课程积累的案例库被不断刷新，相应算法则被不断创新改进。额外成果的产出能帮助提升同学的课程学习成就感和获得感。

（四）课程考核

课程考核能及时检测课程教学效果，并能诊断和反馈学生的学习情况[15]。课程考核以学习主体为依托，从考核周期和考核组织形式两个方面进行课程教学改革，分别有利于推进算法课程的科教融合进程，并培养学生的计算思维能力。

1. “思维导向”的考核周期制订。计算思维是奠基性思维、问题求解思维、逻辑思维、实证思维等多种具体思维模式的交叉融合[16]。

依据表1中课程内容的层次化设置，“深层”内容用于培养学生的奠基性思维，需要贯穿课程教学始终，教师通过提问、抽查等方式不定期考核该层次内容。“中间层”和“浅层”内容主要用于培养学生的问题求解思维。其需要在模块算法结束后，对该模块算法对应的学习小组（组内人员共同感兴趣的算法模块）中相关科研问题的提出，通过报告提交或口头限时陈述等方式进行阶段性特定小组考核。以各同学提交小论文和以小组为单位汇报的形式，进行“结课大作业”考核。该阶段主要考核的指标是学生对科研方向和整个课程内容的逻辑实证思维。作业内容需具有完整性、全局性和准确性。

2. “科研突出”的考核内容制订。依据上述课程改革措施，最终的课程考核内容包括科研问题提出、问题解决和课程算法知识三部分，设置见表2。

科研问题提出发生在课程的前期阶段，由组内成员相互讨论产生。每个算法模块学习结束后，以小组为单位提交的问题设计报告为考核内容。随着课程内容模块不断增加，每个学生的科研问题被反复思考、讨论，最终形成更加明确、完备的创新型研究问题。问题解决则以学生个人小论文和以小组为单位的PPT汇报为考核内容。该部分考核从小组提交科研问题报告并确定报告不再更改时开始，到组内每位成员完成小论文和组代表汇报为止，发生在课程教学的中后期阶段。课程算法知识考核发生在上课间隙，由教师在课堂上交互启发式提问完成。

（五）教学评价

大部分高校的课程评价依赖于教务处成立的专门教学质量评价系统，包括评价指标设置、评价过程实施、评价结果计算和评价结果运用[17]。课程评价的反馈只重视学生群体对教学效果的“一元式”评价结果。这种仅以学生为主体的、单向的评价方式过于笼统，不能“点对点”地展现教学过程中存在的问题。

1. “三方式”评价模式构建。课程应构建“施教方-受教方-导师方”的三方评价机制，形成有效反馈的闭环评价保障体系。

“受教方”指学生群体的课程反馈，可根据教务评价系统的结果进行反馈。而“施教方”为教师。学校需建立面向教师端的教务课程评价系统，教师可通过该系统对不同层级内容教学过程中学生的积极性、认可度、参与度、成果产出率进行评估记录。该记录结果可用于两方面：（1）教师自身后续课程的教学改进参考。（2）教务系统对“施教-受教”双方进行评价对比分析，提出均衡的课程教学改进建议。“三方导向”中的“导师方”，也可称为“目的方”或“社会方”，即课程教学对外形成的社会性、目的性反馈评价。研究生的“导师方”在对本门课程的授课期望、学生学习后的收获和在科研方向上的应用情况进行反馈，促使该课程的教学成果能切实参与到学生的科研成果产出中。

2. “定制模块化”评价指标。依据学生群体的层次化设置小组，为不同的“感兴趣方向”小组提供定制化的课程评价指标。

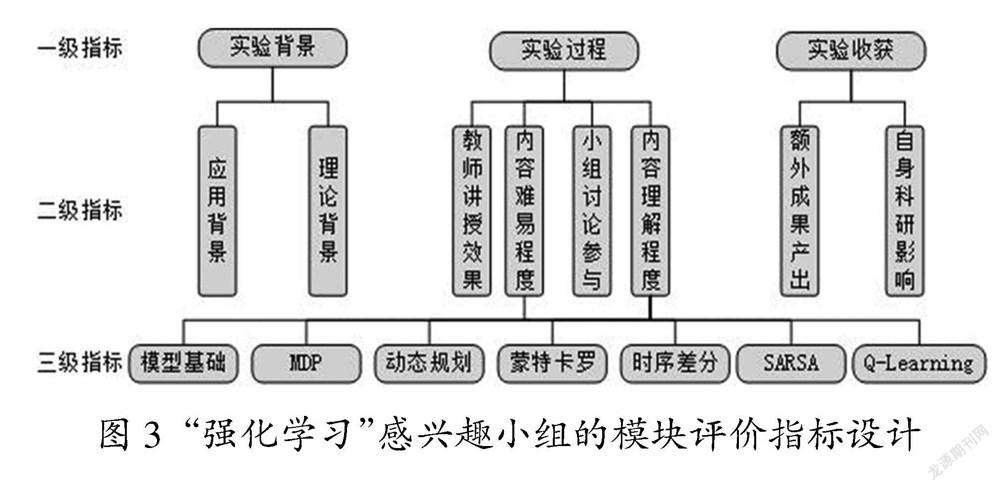
以“前沿科研算法”中的“强化学习”算法为例，可设置三级评价指标，如图3所示。“一级指标”从实验背景、实验过程、实验收获三方面采集学生对各模块的评价情况，以此计算学生在“背景-过程-收获”中的课程学习所得。“二级指标”用于对“一级指标”作展开评价采集，用具体教学过程中的抽象指标描述学生的评估情况，可用于反眏教师、课程内容設置、成果产出、科研进度等方面的课程教学效果。“三级指标”是“二级指标”在学习背景、课程内容、学习成果上的具体描述。以“内容难易程度”和“内容理解程度”为例，分别展开针对强化学习各模块的三级指标，可得出模块内容的教学差异化评估结果。

参考文献：

[1]马海泉，任焕霞.科教融合与全面提高高等教育质量——北京师范大学校长钟秉林访谈录[J].中国高校科技，2012（5）：4-6，11.

[2]温辉，金继承，郭毓东.科教融合助推创新人才培养[J].中国高校科技，2019（3）：55-56.

[3]刘升学，彭仲生，王莉芬.科教融合视域下高校创新人才培养——以南华大学为例[J].教育理论与实践，2020，40（36）：10-12.

[4]陈国良，李廉，董荣胜.走向计算思维2.0[J].中国大学教学，2020（4）：24-30.

[5]潘洪军.高校计算机专业课程结构体系构建的思考[J].现代教育科学，2005（7）：116-118.

[6]刘卫东，张悠慧，向勇，等.面向系统能力培养的计算机专业课程体系建设实践[J].中国大学教学，2014（8）：48-52.

[7]周玉容，张安富，李志峰.中国高等工程教育改革现状，矛盾与转型——基于公立本科院校工科教师的调查分析[J].高教发展与评估，2020，36（3）：14-23+37+109-110.

[8]韩枫.论大学对社会的引领及其实现[D].长春：吉林大学，2020.

[9]史影，周耐明.科研转化实验体系构建与教学探讨[J].实验室研究与探索，2020，39（9）：178-181.

[10]何光全，何思颖.桑代克：成人学习心理学的开创者[J].终身教育研究，2020（4）：70-79.

[11]刘雨薇，李茹.线上线下混合式教学在“算法设计与分析”课程中的应用研究[J].教育理论与实践，2021，41（9）：62-64.