粗糙树状分叉网络多孔介质的有效热导率模型研究

夏永麒， 郑 胜， 杨珊珊*， 易 爽

(1.三峡大学机械与动力学院， 湖北 宜昌 443002； 2.三峡数学研究中心， 湖北 宜昌 443002；3.三峡大学理学院，湖北 宜昌 443002)

树状分叉网络是一种普遍存在的几何结构[1-3]，如血管组织、支气管树、植物脉络、微电子器件散热通道等等.此前研究表明，具有类树状分叉网络的多孔介质，其微通道具有统计自相似的特性，在一定尺度范围内满足分形分布.现实生活中多孔介质的微通道往往不是光滑规整的，而是粗糙各异的.由于热输运性质与微观结构紧密相关，对于树状分叉网络多孔介质，结合微观结构来研究粗糙壁面对于其相关传热物理特性的影响，是很有必要的．

Mandelbrot[4]提出分形理论来表征多孔介质的结构特性；Xu等[5-6]对树状分叉网络介质的热输运性质进行了研究，建立了相应的分形模型；Wang等[7]提出了嵌套树状分叉网络的复合材料有效热导率的分形模型，分析了分叉网络结构参数对于有效热导率的影响；Li等[8]对于生物多孔介质的热输运特性进行了研究并推导了生物多孔介质有效热导率的分布函数.上述关于分叉网络中热输运特性的研究为本文所用的分叉网络模型奠定了基础，但未考虑粗糙特性的影响.粗糙树状分叉网络多孔介质的微结构，在一定程度范围内是满足分形标度律的.Marjumdar和Bhushan[9-10]的关于分形理论的研究表明，在一定条件下粗糙微通道粗糙元满足分形标度律；Chen等[11]利用分形康托集来描述粗糙微通道中粗糙表面的形貌特征，并使用数值模拟的方法研究粗糙微通道的传热特性；Yang等[12]结合分形几何理论得到了微通道中相对粗糙度与表面结构参数之间的无经验常数的关系式.因此，根据以往研究，使用分形理论来研究粗糙树状分叉网络多孔介质的热传输特性是可行的．

本文依据分形几何理论建立了粗糙壁面的树状分叉网络多孔介质的分形模型，推导得出了介质有效热导率的分布函数，并对粗糙特性及树状分叉网络结构参数对于有效热导率的影响进行了分析．

1 粗糙树状分叉网络多孔介质模型

1.1 粗糙元的分形模型

根据Marjumdar和Bhushan[9-10]的关于分形理论的研究，粗糙微通道中壁面粗糙元的分布在一定条件下，也满足分形分布.由于粗糙壁面的粗糙元形态复杂各异，难以计算，以往的研究使用了各种不同形状的模型去模拟粗糙元的形态[13-14].为了使模型适用于更多的情况，引入一个几何因子g来描述不同的粗糙元.g为粗糙元底面积和高的乘积与粗糙元体积的比值，g的取值是可以大于1的，任一形状粗糙元的体积就可表示为：

V=gSihi.

(1)

本模型假设粗糙表面的粗糙元是底面直径为λi，高度为hi的圆锥体，且不同大小的粗糙元的高度直径比ω=hi/λi是相等的.粗糙元的底面直径分布满足分形标度律：

N(L≥λ)=(λmax/λ)Df/2.

(2)

(3)

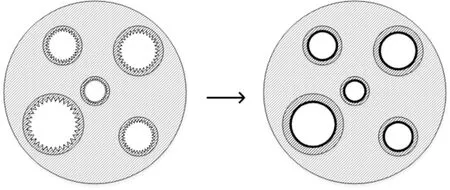
图1 粗糙微通道等效模型示意图Fig.1 Sketch map of rough microchannel equivalent model

1.2 粗糙树状分叉网络分形模型

假设粗糙树状分叉网络多孔介质中，各个不同的分叉树结构具有相同的母管长度、长度比、直径比、分叉角度、分叉级数及每一级的分叉个数，但不同分叉树的母管直径不同，且服从分形分布.

根据分叉网络模型，可以计算引入粗糙元后模型的相关几何参数.根据树状分叉网络的性质，单个光滑壁面树状分叉网络单元的总横截面积[15]为：

(4)

式中，d0为母管的直径，n为树状分叉网络每一级分叉的分支个数，m为树状分叉网络的分叉级数，α=li+1/li为下一级分支与上一级的分支管的长度比，β=di+1/di为下一级分支与上一级的分支管的直径比.因为分形集合单元内树状分叉网络母管直径的分布服从分形标度律，故根据单个树状分叉网络的总横截面积可以积分得到所有树状分叉网络的总横截面积[8]为：

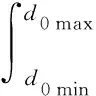
(5)

同理，所有树状分叉网络母管的总横截面积为：

(6)

设介质横截面的孔隙率为φs，根据孔隙率的定义，整个介质横截面的面积为：

(7)

故该多孔介质中树状分叉网络的面孔隙率为：

(8)

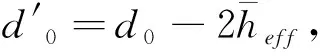
(9)

同时，等效模型中母管直径的改变也会导致横截面孔隙率和母管直径分形维数的变化，如图1.依据孔隙率定义，对于粗糙壁面：

(10)

(11)

故对于具有粗糙壁面的树状分叉网络多孔介质，其所有树状分叉网络的总横截面积、所有母管的总横截面积以及面孔隙率分别为：

(12)

(13)

φ′f=(1-ε)2φf.

(14)

上述式(4)～(14)构成了本文粗糙树状分叉网络分形模型的基础．

2 粗糙树状分叉网络多孔介质有效热导率

2.1 热传导热导率模型

对于光滑壁面类分形树状分叉网络结构，可以根据Xu等[6]提出的串、并联模型，计算树状分叉网络多孔介质的等效热阻.根据傅里叶定律和热电模拟的方法，单个光滑表面分形树状网络的等效热阻rb[16]可以表示为：

(15)

其中，kf为流体的热导率，其他参数与式(4)相同.由式(15)可以看出，一个树状分叉网络的等效热阻实际上是关于母管热阻的等比数列求和，比例系数与长度比、直径比、每一级的分叉个数以及分叉级数有关．

对于粗糙表面的类分形树状分叉网络微通道，需考虑粗糙元等效高度对于母管直径的影响，若忽略流体的流动因素，则具有粗糙壁面的单级母管的等效热阻为：

(16)

又因树状分叉网络的长度比α、直径比β未发生变化(长度未改变，直径改变但易证明直径比不变)，同时分叉结构也未发生变化(m、n、θ未改变)，故母管的长为l0，直径为d′0的单个树状分叉网络的等效热阻为：

(17)

由于不同母管直径大小分布符合分形标度律，可得所有树状分叉网络的热阻为：

(18)

根据傅里叶定律及串并联模型，在不考虑流体流动及对流换热的情况下，介质的等效热导率即为热传导决定，含有随机分布的树状分叉结构多孔介质的有效热导率[8]可表示为：

(19)

式中，Rm为介质基质的热阻，其表达式为：

(20)

L0为单个树状分叉网络的特征长度，其可以表达为：

(21)

将相关参数的表达式代入，可以得到含有随机分布的粗糙树状分叉结构多孔介质的有效热导率[8]表达式为：

kcd=

km[1-(1-ε)2φf]+

(22)

2.2 对流换热的热导率模型

树状分叉网络多孔介质的热输运是一个复杂的过程，在2.1中，忽略了流体与介质基质间的对流换热，但是现实生活和工程实际中，流体与介质基质间的对流换热是不可忽视的．

树状分叉网络多孔介质中的传热包含了介质中的热传导以及流体流动的对流换热两部分的贡献，因此介质传热的有效热导率可以表示为：

keff=kcd+kcv=kcd1+kcd2+kcv，

(23)

式中，kcd为热传导所贡献的热导率，包含介质基质的热导率kcd1以及微通道流体的热导率kcd2两部分组成，kcv表示粗糙表面树状分叉网络多孔介质的对流换热热导率．

一个分形集合单元中所有的粗糙元的总底面面积为：

(24)

假设所有粗糙元具有同样的高度直径比，故可以由粗糙元的底面积得到其侧面积，即分形单元中所有粗糙元的换热面积为：

(25)

无粗糙元覆盖的光滑部分的面积为：

(26)

则由式(25)和(26)可得单个粗糙壁面母管的热对流面积为：

(27)

根据牛顿冷却公式，单个粗糙壁面母管内所有粗糙元的对流换热量为：

qc=hrScΔT，

(28)

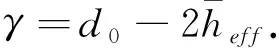
(29)

同一母管在光滑壁面情况下的对流换热量为：

(30)

因此，由式(29)和(30)可知同一母管在具有粗糙表面情况下与光滑表面情况下的对流换热量的比值为：

(31)

通过式(31)可知，η大于1，即表示针对同一母管，粗糙表面会使其对流换热加强，这一比例同粗糙元分布的孔隙率φc，高度直径比ω以及母管的相对粗糙度ε有关．

根据Chen等[17]假设通过树状分叉网络的每一个管道是热充分发展的层流流动，每一级的Nusselt数是相同的，根据树状分叉模型网络的特点，可以得到关于对流换热系数[8]的表达式：

(32)

hi=h0β-i，

(33)

式中，h0和hi分别是第0级和第i级的对流换热系数.根据假设，分叉网络各级之间的温度差是恒定的，故通过单个光滑树状分叉网络的对流换热热流量为：

(34)

对于粗糙壁面的树状分叉网络，由于各级微通道相对粗糙度ε是一致的，且易证明其长度比、直径比等都同光滑表面情况是相等的.故对于粗糙表面的树状分叉网络，上面的处理方式仍然适用.可以得到粗糙壁面树状分叉网络的对流换热量为：

(35)

根据树状分叉网络的结构及粗糙元具有的统计自相似的特性，单个粗糙树状分叉网络的热对流面积为：

(36)

由此可以得到同一个树状分叉网络在粗糙壁面与光滑壁面情况下的对流换热面积的比值：

(37)

仿照迂曲度的定义，将面积比τ定义为树状分叉网络的面迂曲度，用来描述粗糙壁面的凹凸不平的程度，面迂曲度越大，表示壁面凹凸不平的程度越高，对流换热面积越大．

由于多孔介质中的不同树状分叉网络的壁面材质相同，在该模型中可以认为同一介质中的不同树状分叉网络里粗糙元分布的分形维数Ds和孔隙率φc也是相同的.且由于粗糙元的高度直径比ω是定值，故树状分叉网络多孔介质中，对于不同的分叉树，其面迂曲率τ是相等的.因此整个多孔介质的管壁对流换热面积也满足这一比例关系.对于光滑壁面的树状分叉网络，整个介质的对流换热面积及对流换热量为[8]：

(38)

(39)

故对于粗糙壁面的情况，整个介质的对流换热面积及对流换热量为：

Ac=τAs=

(40)

(41)

依据傅里叶定律，流体流动引起的对流换热的热导率为：

(42)

根据母管直径分形分布的概率密度函数，可以得到母管的平均直径为：

(43)

(44)

由式(22)和(44)可得粗糙树状分叉网络多孔介质的有效热导率为：

keff=kcd1+kcd2+kcv=km[1-(1-ε)2φf]+

(45)

由式(45)可以看出，在忽略流体流动影响的情况下，粗糙壁面介质相比同一光滑壁面介质，介质基质热传导增强，流体热传导减弱，对流换热增强．

3 分析与讨论

基于得出的有效热导率表达式，本文计算出了相应介质的热导率，并与该类型介质的实验数据[19-21]进行比较，相关参数的取值见图例注释.图2中对比了不同基质热导率km情况下，粗糙壁面和光滑壁面的树状分叉网络多孔介质的有效热导率的关系.如图2可以发现，根据式(45)提供的有效热导率模型计算出的粗糙壁面树状分叉网络多孔介质的有效热导率与部分文献中的实验结果数据较为吻合，且粗糙壁面有效热导率要大于同等光滑壁面介质的有效热导率，图2取值范围中，传热增强在2.7%～5.8%.图3中表明了基质热传导、流体热传导以及对流换热三个部分与介质总体有效热导率的关系及贡献比重.图2和图3中的参数为kf=0.5，φf=0.1，ε=0.1，α=0.77，β=0.8，n=2，Nu=4.93，δT=25 μm，d0max=3.7×10-2m，d0min=3.7×10-4m.

图2 有效热导率与相关实验数据[19-21]的比较 图3 kcd1、kcd2和kcv分布曲线图 Fig.2 A comparison of effective thermal Fig.3 Distribution curves of kcd1、kcd2 and kcv conductivity with experimental data

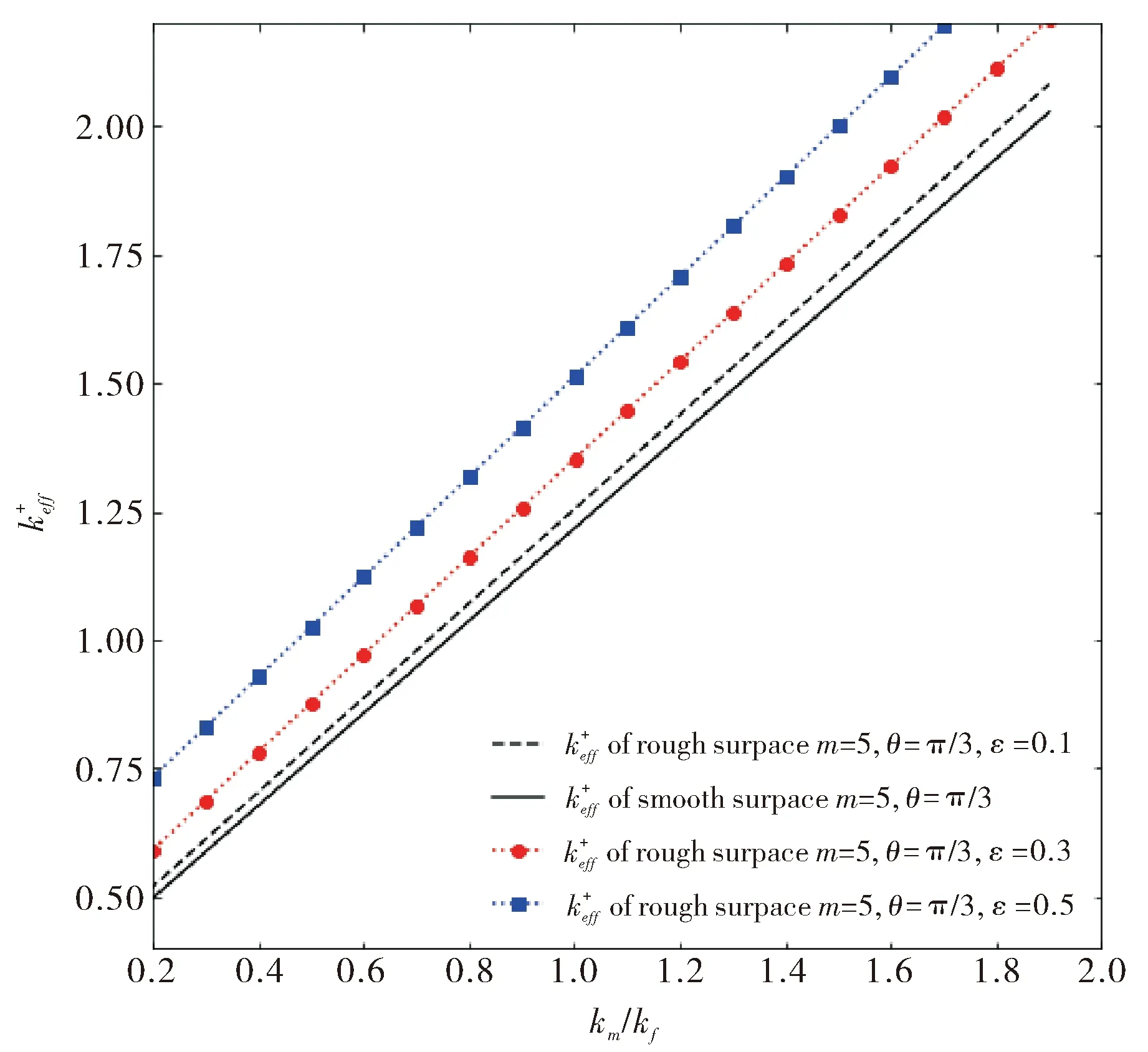
φf=0.1，ε=0.1，α=0.77，β=0.8，n=2，Nu=4.93，δT=25 μm，d0max=3.7×10-2 m，d0min=3.7×10-4 m图4 有效热导率关于km/kf分布曲线图Fig.4 Plot of effective thermal conductivity with respect to km/kf distribution

从图5中可以得到，介质基质的热传导随相对粗糙度升高而增强，流体的热传导随相对粗糙度升高而会减弱，而且两者关于相对粗糙度的变化都相对平缓.在图5取值范围内，对流换热随相对粗糙度的升高迅速升高，介质总体的有效热导率变化曲线也具有相似的趋势.这说明了在该条件下，粗糙壁面对于多孔介质内微通道传热的主要影响是体现在对流换热的增强上，其相对于热传导的影响要更为显著.在相对粗糙度为0.1时，介质有效热导率中，流体热传导部分占比45.1%，基质热传导部分占比7.3%，对流换热部分占比47.6%；相对粗糙度为0.3时，流体热传导部分占比41.6%，基质热传导部分占比3.9%，对流换热部分占比54.5%．

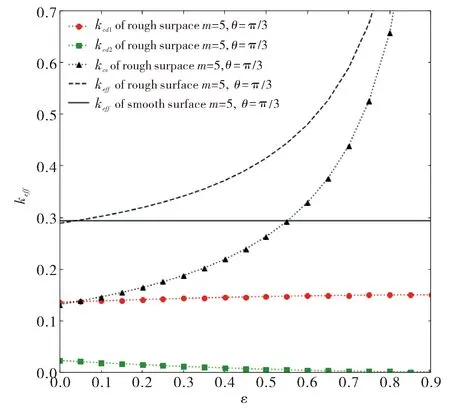
km=0.15，kf=0.5，φf=0.1，α=0.77，β=0.8，n=2，Nu=4.93，δT=25 μm，d0max=3.7×10-2 m，d0min=3.7×10-4 m图5 有效热导率关于相对粗糙度的分布曲线图Fig.5 Plot of effective thermal conductivity with respect to relative roughness

图6说明介质基质的热传导随母管孔隙率增大而减弱，流体热导率随母管孔隙率增大而增强，对流换热随母管孔隙率增大而增强.最终介质总体有效热导率的变化是三者综合决定的，在图示条件下，对流换热占据主导作用.相比同等光滑介质，具有粗糙壁面的树状分叉网络多孔介质的有效热导率更大．

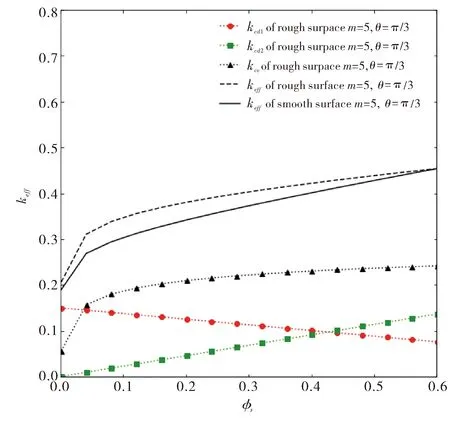
km=0.15，kf=0.5，ε=0.1，α=0.77，β=0.8，n=2，Nu=4.93，δT=25 μm，d0max=3.7×10-2 m，d0min=3.7×10-4 m图6 有效热导率关于母管的孔隙率的分布曲线图Fig.6 Plot of effective thermal conductivity with respect to the porosity of the parent tube

4 总结

根据分形理论和传热学定律，建立了粗糙壁面树状分叉网络多孔介质的分形模型，通过一系列合理的简化和假设，推导出了粗糙树状分叉网络多孔介质的有效热导率分布函数.通过分布函数得出的有效热导率与之前部分学者研究的实验数据较为吻合.同时，结合推导的分布函数，分析了有效热导率与相对粗糙度、基质(或流体)热导率、母管直径孔隙率等参数的内在联系，为后续的实际应用和模型完善提供了一定的理论依据．