浅谈数学概念教学四个要点

薛少满

摘 要：数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式，即一种数学的思维形式。在数学中，作为一般的思维形式的判断与推理，以定理、法则、公式的方式表现出来，而数学概念则是构成它们的基础。对于不同的数学概念，我们教师如何采取不同教学方法，在数学概念的教学过程中让学生更好地正确理解并灵活运用数学概念，这是学生掌握数学基础知识和运算技能、发展逻辑论证和空间想象能力的前提。

关键词：数学概念;概念教学;椭圆概念

数学来之于生活而又高于生活，所以数学概念具有抽象性与具体性。中学数学概念无论如何抽象，实际都有它的具体内容和现实原型。在教学中，要注意学生的生活经验与动手操作能力的培养。下面以《椭圆及其标准方程》这节课为例，浅谈数学概念教学四个要点。

一、概念的引入

概念的引入，通常有两类：一类是从数学概念体系的发展过程引入，一类是从解决实际问题出发的引入。“椭圆及其标准方程”这节课，着重从实际问题引入，通过创设实验活动，培养学生动手操作能力，让他们在亲自体验实践中形成数学概念。教师根据学生情况可以创造不同实践，供参考实践活动一：通过传统作图方法展示椭圆作图过程，也就是在黑板上固定两个小铁钉设为点F1和F2，一根无弹性细绳绕在一支粉笔（M点）上。拿着粉拉直细绳，在黑板上画出动点M的轨迹，即可得到椭圆，并且通过变动两个小铁钉的位置，或者改变细绳长度，可以得到不同离心率的椭圆。优点：这种“传统”的引入方法，具有极强的生命力，说明其存在的合理性。缺点：体现不出与已学的圆之间的关系。

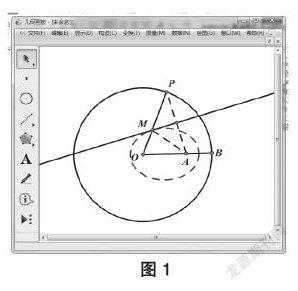
实践活动二：在现代教学中，多媒体已经深入课堂，教师可通过信息技术展示椭圆的生成过程，下边以“几何画板”为例展示，如图1：

构造步骤：

（1）作一半径为2a的圆，在圆上取一点B，P，连结OB、OP;

（2）在线段上取一点A（点A为线段OB上的动点），连结AP;

（3）作AP的垂直平分线，交OP于点M;

（4）把点M定义为动点P的“跟踪点”，即可得点M的轨迹为椭圆。

绘图原理：图中|MO|+|MA|=|MO|+|MP|=2a，满足椭圆定义，同时可改变点A在线段OB的位置，得到不同离心率的椭圆。

优点：可以通过动画直观生动地突出突椭圆轨迹的生成过程，同时移动点A与点O重合就是圆，与B重合时就是线段OB;缺点：学生只能坐着看教师的整个操作过程，被动接受椭圆的概念。

实践活动三：每个学生准备一张圆形纸片，做一个折纸游戏，要求如下：

（1）在圆形纸片内取异于圆心F1的定点 F2;

（2）将圆形纸片的边缘向内折叠，使圆形纸片的通过定点F2，或者说使原纸片边 缘上的一点A与点F2：重合（图2）;

（3）每取一次点A就得到一条折痕;

（4）通过不断地操作，使折痕足够密集（图3、图4）。

优点：有一定的新意，能有效激发学生的探究热情;缺点：折痕只能得到一个近似的椭圆，教师还要对这个游戏进行有效抽象。

不管进行怎样的实践活动，教师首先对自己所教学生的学情进行学情分析，选择适合他们思维起点的实践活动，进行有效教学。

二、概念的形成

通过创设一种活动情境，实践活动引导学生亲自实验或通过现代教育技术手段演示及自己操作（如“几何画板”）对数学概念有一个感性认识，去领悟数学概念的形成，然后再通过理性分析与理解概念的形成。回归《椭圆及其标准方程》一节，通过实践活动，学生已对椭圆有了一定的感知认识，教师可再设置一定的思考问题，让学生在思考中慢慢形成概念，椭圆的定义可以与以前已学圆的概念类比，设计问题。圆的定义：在一个平面内，到定点距离等于定长的点的轨迹叫做圆。

问题一：通过一个定点可作得一个圆，作得一个椭圆，通过几个定点？

问题二：圆上的点到定点的距离等于定长，那椭圆上的点也有类似的特点吗？

问题三：当椭圆的两个定点慢慢靠近的时候，椭圆的形状有什么变化？

问题四：当两定点重合一起时得到一个什么图形？

问题五：刚才作出椭圆图形的时候，我们观察到绳子的长度比两定点的距离大，如果绳子长度等于两定点距离长时能作出一个椭圆吗？如果不能，只能作出什么图形？

问题六：如果绳子小于两定点距离长时能作出什么图形？

衡量一名学生是否掌握一个概念的本质不在于能否用简单的语言将数学概念表达出来，而是要真正理解概念的内涵和外延。因此，在概念的教学中，教师要指导学生反思概念形成的过程，深刻理解概念的本质特征。上述通过层层设问，学生通过思考，形成严谨的思维，到底满足怎么样条件的情况才能得到一个椭圆，从而形成椭圆概念。

三、概念的概括

通过实例或实践活动，引导学生思考，进行讨论，从而形成概念。因此，数学概念的形成实质上是抽象出数学对象的共同本质特征的过程。再看《椭圆及其标准方程》一节，椭圆的概念是发生式定义，教师还要对椭圆概念概括，明确概念，完善概念。

（一）给出课本椭圆概念的描述：“平面内到两个定点F1、F2的距离之和等于常数（大于|F1F2|）的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距”。

（二）总结问题探究：

（1）若常数大于|F1F2|， 则点M的轨迹是（椭圆）;

（2）若常数等于|F1F2|，则点M的轨迹是（ 线段）;

（3）若常数小于|F1F2|，则点M的轨迹是（不存在）。

（三）进行椭圆的轨迹方程的推导（数学运算也是数学素养的一种）：

（1）建系;（2）设点：M（x，y）;（3）列式;（4）代坐标;（5）化简，整理。

在概念的概括過程中，除了理解椭圆概念，还要掌握椭圆方程，而椭圆的轨迹方程的推导有些费时间，但提高运算能力，这也是学好圆锥曲线的重要部分。有个别教师可能为了省时，跳过推导，直接给出椭圆的标准方程，这个推导运算量大，教师可以根据学生的情况，进行引导式推导，从而提高学生的运算能力，使学生掌握求轨迹方程类问题的推理能力。

四、概念的应用

学生对概念理解与否，最后还要做相关习题来方法检验，通过检验才能了解学生掌握知识的情况，通过运用所学知识解决问题，才能使学生更深刻理解所学知识，灵活运用所学知识。而教师选取合适、典型的习题也是一节课的关键。

《椭圆及其标准方程》一节，根据教学要求：（1）理解椭圆概念和会求椭圆标准方程;（2）能利用椭圆概念解决一些简单的问题。选取课本例题：已知椭圆的两个焦点分别是（-2，0），（2，0），并经过，求它的标准方程。通过分析，可引导学生用两种方法解答。法一：可由椭圆定义先求出2a，又已知c，故可求出方程;法二：由焦点坐标知道a、b关系，再将已知点代入椭圆方程。设计意图：检验椭圆概念理解掌握情况，以及两种标准方程形式的判别。堂上学生练习：

设计意图：检验是否会求两种椭圆标准方程。

恩格斯说过：“在一定意义上，科学的内容就是概念的体系。”数学就是由概念与命题组成的逻辑体系，而数学概念就是整个逻辑体系里面的细胞，只有教师重视数学概念教学，才能使这些细胞赋予生命。

参考文献：

[1]李一鸣.“椭圆及其标准方程”教学设计[J].中学数学教学参考，2018-12.

[2]张厅剑.数学概念教学的误区及对策[J].中学数学教学参考，2016-12.