聚焦基本图形 渗透一般观念

⦿太湖县实验中学 周阳明

平面几何是初中生学习数学的一大障碍，对于几何题，学生们普遍感觉是难、很难.尤其是图形繁杂一点的几何题，那更是雾里看花，大海里捞针，无从下手，没思路.对此，笔者结合自身教学实践及参加市级课题“一般观念引领下的中学数学几何教学研究”所学理论对这类现象略作出分析思考，认为几何教学要关注基本图形，渗透一般观念，帮助学生提高解题能力.一家之言，以期抛砖引玉.

1 基本图形的意义及分类

基本图形指的是蕴含了一些特定性质和应用条件的几何图形，它是构成几何图形的细胞，一个个这样的细胞通过叠加或者删减线段构成了灵动优美的平面几何图形.在解决几何题时如果能发现、聚焦几何图形就能加深对题中数量关系及位置关系的理解，从而快速发现解题思路.离开基本图形去讨论几何题的解法无异于缘木求鱼，学生只能机械地得到一些解题经验，而不能得到科学的解题方法.

初中几何中常见的基本图形有30多个，例如与平行线有关的“三线八角”、等腰三角形、直角三角形斜边上的中线、全等三角形、相似三角形、特殊角三角形、垂径定理等.

2 基本图形的应用

如何聚焦基本图形呢？首先要明确每个基本图形的应用条件和具体结论，然后根据题目的条件找出图中的基本图形，此过程中可能要添加辅助线补充出基本图形.教师在平时的日常教学中要有追求直观的意识，培养学生从复杂图形中找出基本图形，分离式补全基本图形以及应用基本图形性质的能力.下面结合教学中的一个案例来进行分析.

例题如图1，△ABC中，AB=AC，点D，E，G分别为线段BC，AD，AC的中点，DF⊥BE交BC于点F.求证：FG=DG.

图1

与中点有关的基本图形有三角形的中线、三角形的中位线、三角形的重心、等腰三角形的三线合一、直角三角形斜边上的中线、平行四边形的对角线、直径已知的圆、垂径分弦、线段的垂直平分线等.

2.1 从已知图形中找出基本图形

分析：由∠DFE=90°，需证FG=DG，可联想到直角三角形斜边上的中线等于斜边的一半这一基本图形，从而延长FE和DG交于点H(如图2)，连接EG.利用三角形的中位线和相似三角形里的“A字型”这两个基本图形来证明G为DH的中点，从而证出FG=DG.

图2

2.2 从结论出发联想构造基本图形

分析：从线段的垂直平分线出发寻找思路.因为要证FG=DG，只要证明点G在线段DF的中垂线上.如图3，过点G作GN⊥DF交BC于点M，垂足为N.于是四边形EGMB是平行四边形，则2EG=2BM=BD.根据直角三角形斜边上的中线等于斜边的一半或平行线等分线段知FN=DN，故点N是线段DF的中点，从而得证.

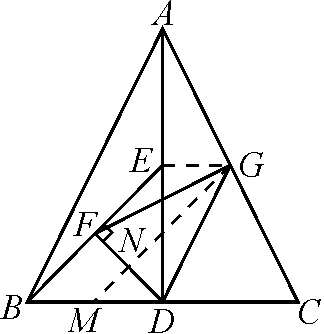
图3

2.3 利用图形中的点或者线段联想基本图形

分析：由中点加直角联想到基本图形，直角三角形斜边上的中线等于斜边的一半(已知直径的圆)，由此出发寻找解题思路.本题中的已知条件出现了AB=AC，点D为BC的中点，所以可以应用等腰三角形中重要线段的基本图形的性质，从而得到∠ADC=90°.这是本题中的第一个基本图形.

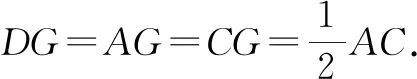
图4

证法3：如图4，连接AF，CF.

因为DF⊥BE，所以∠BFD=∠DFE=90°，则∠CFD+∠CFE=90°.

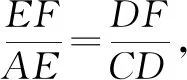
故FG=DG.

通过例1的分析，可以发现这一道复杂的几何题实际上就是由几个基本图形组成的，分别找到这几个基本图形，把它们分离或补充出来，再根据这些基本图形的性质，经过简单推理就能得出结论.从教学实际看，学生在掌握聚焦基本图形这一分析方法后能触类旁通，发展一般观念，掌握几何问题的分析思考方法，能一看就明白，一想就出来，充分体会到数学的逻辑美、严谨美和成功的喜悦.

3 几点思考

3.1 教学中要重视基本图形

基本图形对学生学好几何、提高解题能力有着举足轻重的作用.教师在日常教学中要引导学生认识基本图形，帮助学生理解基本图形的应用条件和性质；要精心设计例题，对课本中的例题进行合理变式，帮助学生掌握基本图形的性质，获得基本的数学经验；不能一味地赶进度，或者觉得知识简单、学生应该容易懂就一带而过，然后光注重刷难题；要重心下移，注重夯实基础，反复打磨，对于体现通性通法的的好题要舍得下功夫.

3.2 聚焦基本图形，重视几何直观，体会思想方法贯通

大多数情况下，学生解决几何问题都是看出来的，而不是证出来的.这就说明学生解决几何问题更倾向于直观想象，靠的是直觉.因此，教师在日常教学中要有重视学生直观思维能力的意识，要注重对学生几何直观能力的培养，着重培养学生“看”的能力：能从已知条件和已知图形中发现基本图形，分离基本图形；从结论、特殊点或线段联想基本图形，聚焦基本图形并对图形进行逻辑推理、模型应用.同时，还要注重引导学生体会数学思想方法，并内化解题经验，优化自己的数学知识结构，从而提高学生几何构图能力和解题能力，真正做到看得出、想得明白.

3.3 重视一般观念，发展核心素养

一般观念是指在不同问题或者同一类问题中存在的相同规律和思想方法，它是学生思维能力的一个指标特征.而数学教学的一个重要任务就是在传授知识的同时，让学生的思维能力得到提高与发展.日常教学中应当从头到尾将学生思维能力的培养与发展放在重中之重的地位.因此，由一般观念出发，发展学生思维能力就是发展学生数学核心素养，而解决初中几何问题又是提高学生数学素养的一个重要途径，它是在“看”和“想”的过程中逐步积累的.这就要求我们的数学教学应根据具体的教学内容，从图形出发，分离或补充出基本图形，设置合适的阶梯问题，逐步引导，让不同层次的学生都能积极参与进来，引发学生思考与交流.问题的解决是学生经历从不同角度寻求分析问题、解决问题的方法的过程，体会数学的思想美和思维美，掌握分析解决一类问题的一般观念.同时，教学中还要引导学生学会多视角、多层次地思考问题，通过“一题多解”“一题多变”“多题一解”“逆向求解”等激发学生学习数学的兴趣，体会不同问题之间蕴含的共同特征、一般规律，发展学生不同方面的思维能力，形成和发展学生的数学核心素养.