基于回归分析的乙醇偶合制备C4烯烃研究

＊陈佳硕 冯明伟

（黑龙江八一农垦大学 黑龙江 163711）

1.研究背景

C4烯烃广泛应用于化工产品及医药的生产领域，乙醇是生产制备C4烯烃的原料。在制备过程中，催化剂组合与温度将对C4烯烃的选择性和C4烯烃收率将产生影响。因此通过对催化剂组合的设计，探索乙醇催化偶合制备C4烯烃的工艺条件具有非常重要的意义和价值。

2.模型的建立与求解

(1)问题一的模型建立

假设温度与C4烯烃选择性和乙醇转化率有关系，根据数据画出散点图，由于数据图像并非呈完全的线性关系，因而对数据进行最小二乘法回归分析，得到所需关系表达式。

给定函数α=f(T)在点T1,…Tn处的函数值对应相应的α1,…,αn求解多项式

建立方程：

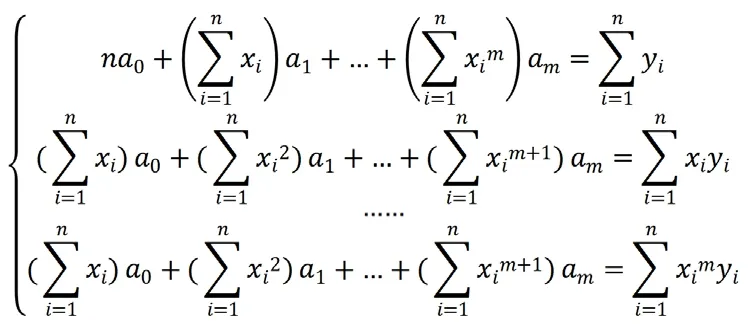
求解方程得到：a0，a1，…am一些列系数，进而得到多项式表达式：

f(x)=a0+a1x+…+amxm

得到温度和乙烯转化率建立如下模型：

α=a0+a1T+…+amTm

对于温度和C4烯烃选择性建立如下模型：

β=a0+a1T+…+amTm

经SPSS相关性运行，得到以下四种测试结果：乙醇转化率、乙烯选择性、乙醛选择性、碳数为4-12脂肪醇选择性。

对于时间和上诉四种测试结果建立如下模型：

时间和乙醇转化率模型：

α=a0+a1t+…+amtm

时间和乙烯选择性模型：

β1=a0+a1t+…+amtm

时间和乙醛选择性（β2）模型：

β2=a0+a1t+…+amtm

时间和碳数为4-12脂肪醇选择性（β3）模型：

β3=a0+a1t+…+amtm

(2)问题一的模型求解

①乙醇转化率与温度关系求解

根据不同催化剂条件下，对于温度和乙醇转化率数据进行绘制散点图，通过散点图确定温度与乙醇转化率关系，运用最小二乘法进行一元线性回归，求解得到类似的关系式：

A1：α=141.807429-1.193926T+0.002545T2

B1：α=121.496695-0.950269T+0.001887T2

②乙醇转化率与温度关系求解

根据不同催化剂条件下，对于温度和C4烯烃选择性数据进行绘制散点图，通过散点图确定温度与C4烯烃选择性关系，运用最小二乘法进行回归处理，求解得到如下关系式：

A1：β=-190.783429+1.422246T-0.002113T2

B1：β=43.031663-0.388761T+0.000993T2

③350度给定催化剂组合实验测试结果求解

时间与测试结果相关性求解如表1。

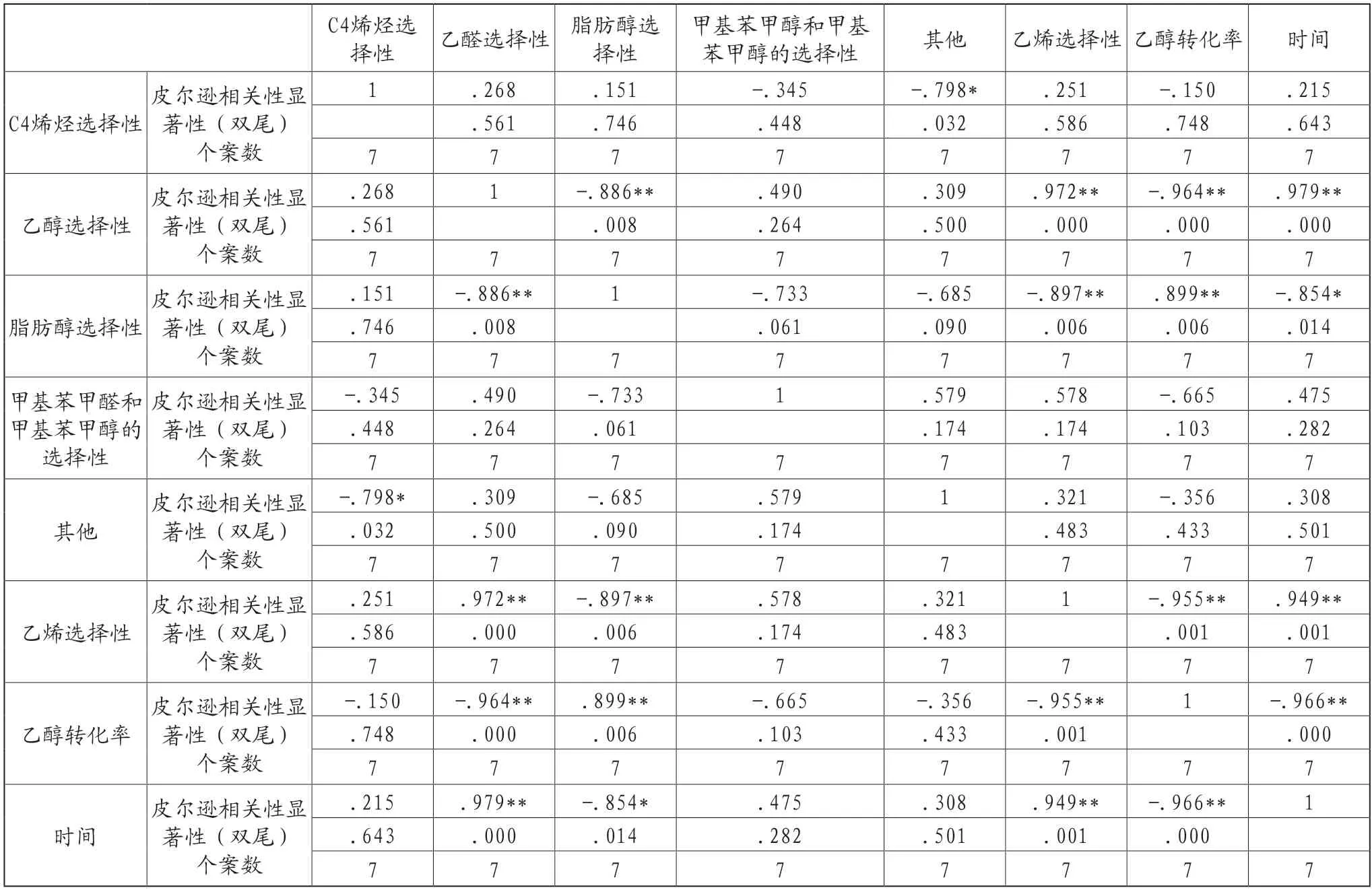
表1 测量结果相关性

根据相关性求解得到：在350°时给定的催化剂组合条件下，时间对于测定实验结果有4种结果有显著的相关性影响，分别为：乙醇转化率、乙烯转化率、乙醛转化率、碳数为4-12脂肪醇。

研究在350°时给定的催化剂组合条件下，时间的变化对于上述4种结果影响分析。绘制散点图，利用回归模型最小二乘法，进行求解得到如下表所示关系式：

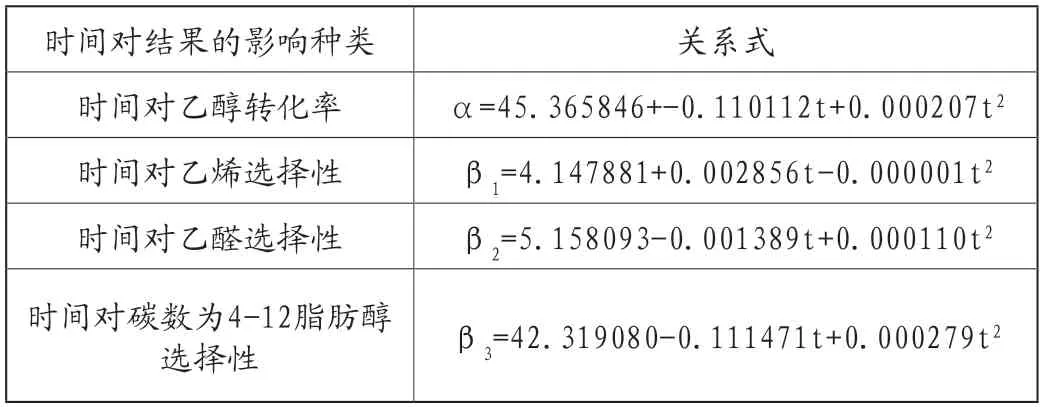
表2 时间对测量结果影响

(3)问题二的模型建立

研究双因素对单因变量的关系，我们将不同催化剂组合在不同温度下的乙醇转化率和C4烯烃选择性大小图表进行填充。

多元回归分析需要多个影响因素的对应值，因实验中存在催化剂组合因素，催化剂组合作为排列方式不能进行数值计算。假设催化剂组合可以用数值代替，我们将其进行数值化从1-21对催化剂组合进行可视数据化，且用C来代替催化剂组合。

构建矩阵：

X=[P1,….P1,P2,…P2,…,C21,…,P21;T1 T2 T3 T4,…,T6T1….T6]

其中数据催化剂组合P1-P21及温度T1 T2 T3 T4 T5 T6分别有126个数据。

Y=[相应的乙醇转化率数值] Y=[相应的C4烯烃选择性的数值]

建立如下多的多元线性回归模型：

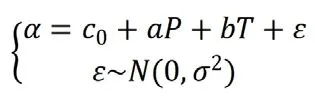
将催化剂组合和温度对乙醇转化率以及C4烯烃选择性分别运用对应分析模型[4]，通过对应分析模型，加权进行主成分分析，进而寻求列联表的行和列之间的低维度图表示。

根据多元线性回归和对应分析所得低纬度图示，可见得催化剂组合对于乙醇转化率以及C4烯烃得转化率并无较为明显关系。

由第一问可知乙醇转化率以及C4烯烃选择性与温度有明显关系，可通过乙醇转化率和C4烯烃选择性对温度的影响，反其道而行之得温度对乙醇转化率以及C4烯烃转化率影响，将乙醇转化率以及C4烯烃选择性与温度建立相关模型：

(4)问题二的模型求解

STEP1：利用问题1所求解相关表达式，求解不同温度下乙醇转化率和C4烯烃选择性在其他温度下缺失值，得到如表1所示的全部数据。

STEP2：将催化剂组合用数值1-21进行可视数据化表示，将可视化催化剂组合与温度和相应的乙醇转化率及C4烯烃转化率分别进行多元回归分析。

STEP3：运用MATLAB求解[1]得到如下所示关系。催化剂组合和温度对乙醇转化率的影响：

表3 MATLAB程序的计算结果

回归方程：

α=-1.3775P+0.3437T-71.6925

R2=0.6900（说明呈现一定的相关性但相关性不显著）

催化剂组合和温度对C4烯烃选择性的影响：

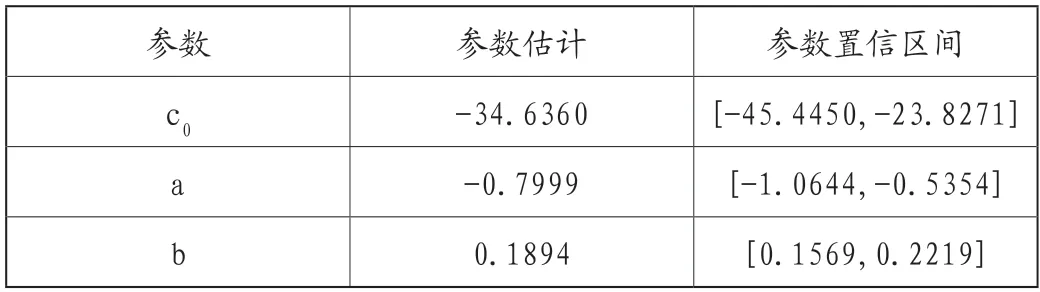
表4 MATLAB程序的计算结果

回归方程：

β=-0.7999P+0.1894T-34.6360

R2=0.5788（说明呈现一定的相关性但相关性不显著）

STEP4：将数据带入对应分析模型，通过绘制低纬度图，分析催化剂组合数和温度对于乙醇转化率和C4烯烃选择性的影响。

图1 对应分析乙醇转化率关系图

图2 对应分析C4烯烃吸收率关系图

图表结论：从表中可以看出催化剂组合相对于温度对于转化率和C4选择性，催化剂组合在图标中较为分散，说明催化剂组合与其相关性较弱。

STEP5：因将组合数看作数值存在较大误差，我们将组合数当作固定因素不进行分析，将温度作为因变量，将C4烯烃吸收率和乙醇转化率作为自变量研究其存在关系，进而得到温度对C4烯烃吸收率和乙醇转化率的影响。

运用SPSS对温度和C4烯烃吸收率及乙醇转化率进行求解分析得以下关系：

A1：T=2.021β+2.012α+181.024，相关系数R2=0.982

B1：T=6.792β-2.315α+221.884，相关系数R2=0.981

3.模型评价与推广

(1)模型优点

①模型一运用回归模型将不同催化剂种类条件下，进行最小二乘法回归拟合得到相应表达式，使得实验数据更具说服力。

②模型二运用对应分析模型将数据绘制于图表进行降维图表分析，使得关系更加可视化分析，同时用温度与两因素关系反向推到温度对其造成影响。

(2)模型缺点

模型在数据处理上，存在部分较为模糊的处理，使得存在一定的误差和容错率。在多元回归模型分析时，将催化剂组合整合为数值进行计算，导致实验存在一定的误差，相关性较弱。同时因实验数据有限，模型只能对有限范围内的数据结果进行分析。